拨开云雾见天日 守得云开见月明——一道期末检测题的解题研究

张雪芳

(萧山中学，浙江 杭州 311201)

《普通高中数学课程标准(2017年版2020年修订)》指出，数学教育承载着落实立德树人根本任务、发展素质教育的功能.数学教育中的立德树人要体现数学学科特点，具体而言就是发展学生的核心素养，而聚焦点应该放在理性思维和科学精神的发展上，这是由数学的学科特点决定的[1].习题是数学学习的一个载体，是发展学生数学思想方法的土壤.解题过程是一个思考的过程，是发展学生数学核心素养的一个抓手，在解题教学的过程中可以培养学生的理性思维和科学精神，蕴涵着学科育人的潜能．笔者以一道期末检测题为例，分析学生的思维过程，探寻问题本质，与同行分享.

1 原题呈现

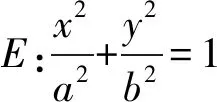
1)求椭圆E的标准方程；

(浙江省杭州七县(市、区)2020学年高二第一学期期末数学学业水平测试第22题)

从而

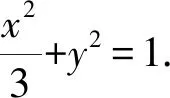
整理得 (3-4m2)k2+8mnk+3-4n2=0.

其两根k1,k2满足

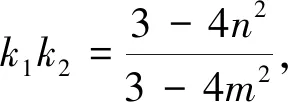
(1)

这里k1=kOA，k2=kBA,且

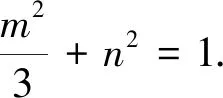
(2)

设A(x1,kx1)，B(x2,kx2),则

由式(1)和式(2)，得

当且仅当|OA|=|OB|时取等号，即

批阅10 647位学生的解答，该题的平均得分为3.9分.在求|OA|+|OB|的最大值时，很多学生首先求得|OA|+|OB|的表达式，然后求其最大值，但是表达式十分复杂，变量有两个，求最值束手无策.参考答案是先计算|OA|2+|OB|2为常数，然后运用不等式得到|OA|+|OB|的最大值.当看到参考答案的解题过程时，学生们不是恍然大悟而是纷纷质疑：怎么想到先算|OA|2+|OB|2的呢？

问题是核心素养的生长点，解题教学不是将现成的巧妙方法与过程灌输给学生，而是带着问题追本溯源.顺应学生的思维，本题要解决两个问题：1)得到|OA|+|OB|的表达式后，能不能求出最值？怎么求出最值？2)为什么|OA|2+|OB|2是常数？是偶然还是必然？

2 通解通法

通过计算可得

(3)

(4)

通分处理后表达式更烦琐了，那么回到问题本身，二元函数通常如何求最值呢？消元，化二元为一元.

这是关于k1的函数表达式，结构比较复杂，如何化繁为简？整体换元.

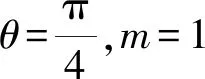
根据算术—几何平均值不等式可知

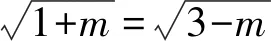
回顾上述运算过程，先对多元函数消元，再是通过多次换元化繁为简，从而使表达式的结构特点完全“暴露”，最后根据结构特点可用多种方法求得最值.每一步等价转化都蕴藏着数学运算与逻辑推理等核心素养，需要学生们有扎实的基本功和“咬定青山不放松”的运算毅力.

3 利用不等式求最值

代数结构中往往透露着解题方法，怎样才能“看见”？需要教师在平时的解题教学中引导学生从多个视角去观察与发现，“前行莫忘来时路”，回归原点分析式子，体会等价变形前后的异曲同工.

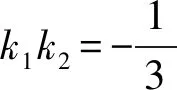
4 一般探究

|OA|2+|OB|2=a2+b2.

即

于是

则

故

|OA|2+|OB|2=a2+b2.

即B(-asinθ,bcosθ),故

|OA|2+|OB|2=a2cos2θ+b2sin2θ+a2sin2θ+b2cos2θ

=a2+b2.

|OA|2+|OB|2=a2+b2，

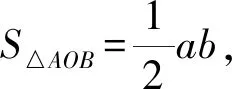
5 追本溯源

解法1设⊙G:(x-m)2+(y-n)2=r2的切线OA(OB)的方程为y=kx，则

整理得 (m2-r2)k2-2mnk+n2-r2=0,

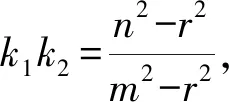
从而

于是

即

图1

解法2如图1，设OG与x轴正半轴所成角为θ，|OG|=ρ，设G(ρcosθ,ρsinθ)，则

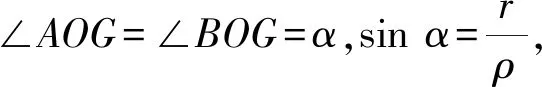
从而k1k2=tan(θ+α)tan(θ-α)

即

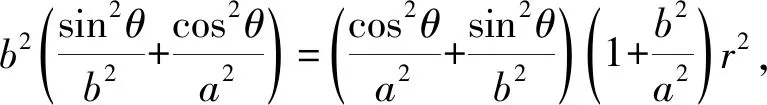
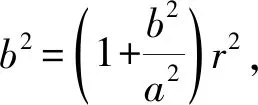
即

罗增儒教授指出，数学学习中发生数学的地方无一例外地充满着数学解题活动，数学教学要“以解题为中心”，解题过程就是学习新知、发展智力、提高能力的过程[2].碰到解题困难,“掉转枪头找捷径”不是唯一出路，教师要带领学生用“通性通法”攻克难关，体验“在常规中显功底，在平淡中见本质”的过程.教师要引领学生在观察与发现中积累基本活动经验，在解题反思中挖掘问题“源”；少一些“秒杀”的方法，多一些“秒杀”背后的原因探究，这样学生才能由“知其然”到“知其所以然”，进一步发展为“知何由以知其所以然”，最终提升学生的数学核心素养，促进可持续发展.