一种仿生四足机器人腿部机构的运动学分析与验证
王晓磊,刘 祥,张强池
(辽宁工业大学机械工程与自动化学院,辽宁 锦州 121001)
1 引言
近年来,仿生四足机器人在抢险救灾、军事训练、野外科考等诸多领域内发挥着重要作用[1],新型仿生四足机器人的设计也逐渐成为机器人研究领域中的热点。腿部机构为机器人运动的主要驱动机构,它的结构设计是机器人整机设计的基础[2],对机器人的整机运动性能起到了决定性的作用[3]。
目前仿生四足机器人的腿部机构多以串联机构为主,其中比较有代表性的有美国波士顿动力公司研制的BigDog[4]与Lit‐tleDog[5]。串联机构机械腿的设计与控制比较简单,具有较强的运动灵活性,机器人的工作空间也相对较大,但自重载重比较大,负载能力相对较低。文献[6-9]采用并联机构机械腿设计仿生机器人,相比于串联机构机械腿,并联机构机械腿的足端与动力输入端存在多条支链,使得机械腿的结构更加稳定,具有更强的负载能力,但工作空间相对较小[10]。串并混联机构机械腿同时综合了串联机构和并联机构的优点,既具有较高的承载能力,运动的灵活性也相对纯并联机构要强,可以得到较好的运动学与动力学性能[11],因此有研究人员将串并混联机构引入四足机器人腿部构型中,如文献[12]开发的三种串并混联式机械腿,并在样机的基础上证实了串并混联机械腿的优越性。
为拓展串并混联机构在四足机器人中的应用,这里提出了一种具有行程放大的串并混联结构仿生机械腿,搭建了机器人的整机模型;建立了腿部结构的空间三维坐标系,推导了位置方程的正反解,求解了机器人腿部机构的工作空间;基于位置方程推导出腿机构的速度雅克比矩阵;利用虚拟样机技术完成了四足机器人单腿模型的运动学仿真。通过仿真结果与理论结果的对比,验证机器人模型与理论分析的正确性。
2 仿生四足机器人的结构介绍
这里所研究的四足机器人主要由机架和四条串并混联机械腿组成,如图1所示。四条机械腿具有相同的结构形式,过腿部机架与机器人机架相连,如图2 所示。每条机械腿由一并联机构和一串联机构组成。并联机构由一平行四边形机构和两个直线电缸组成,两个直线电缸伸出或缩回的协调运动可以实现足端的前后摆动和上下移动。串联机构由一直线电缸驱动,实现腿部并联机构的侧向摆动。该四足机器人腿部主体采用缩放式结构,通过两组平行四边形机构的叠加,使腿部足端的运动空间实现缩放功能,同时也提高了腿机构的刚度与承载能力。

图1 四足机器人整机模型Fig.1 Complete Machine Model of Quadruped Robot
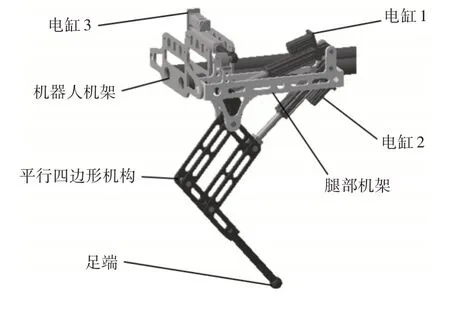
图2 四足机器人单腿模型Fig.2 Single Leg Model of Quadruped Robot
3 四足机器人腿机构运动学分析
3.1 腿机构坐标系的建立
四足机器人腿机构坐标系的建立是对机器人定量分析的前提,是后续运动学分析和仿真验证的基础。腿部机构简图及坐标系建立,如图3所示。ABCQ为一平行四边形机构,杆AB延长线的D点为足端参考点,AQH为同一杆件,HG、CF分别为并联机构的驱动电缸1和2的长度,MN为侧摆驱动电缸3的长度,SKL与机器人机架相连,PT是侧摆旋转轴,QO与旋转轴固连。设沿PT方向为X轴,Y轴垂直于X轴并在机架平面SKL面内,Z轴通过右手螺旋定则确定。设腿部机构的主要几何参数为QC=AB=a、QA=BC=b、BD=c、QH=d、PM=NK=j、OQ=h、QG=f、QF=e、OK=i,HG=l1、CF=l2、MN=l3、QE为过Q与X轴平行的直线。∠AQE=θ1、∠AQC=θ2、∠HQE=θ3、∠CQE=θ4、∠HQG=θ6、∠CQF=θ9、∠AQH=θ5、∠FQE=θ7、∠GQE=θ8、∠KPN=θ11,其中θ5、θ7、θ8、θ11的角度值为固定参数不变。
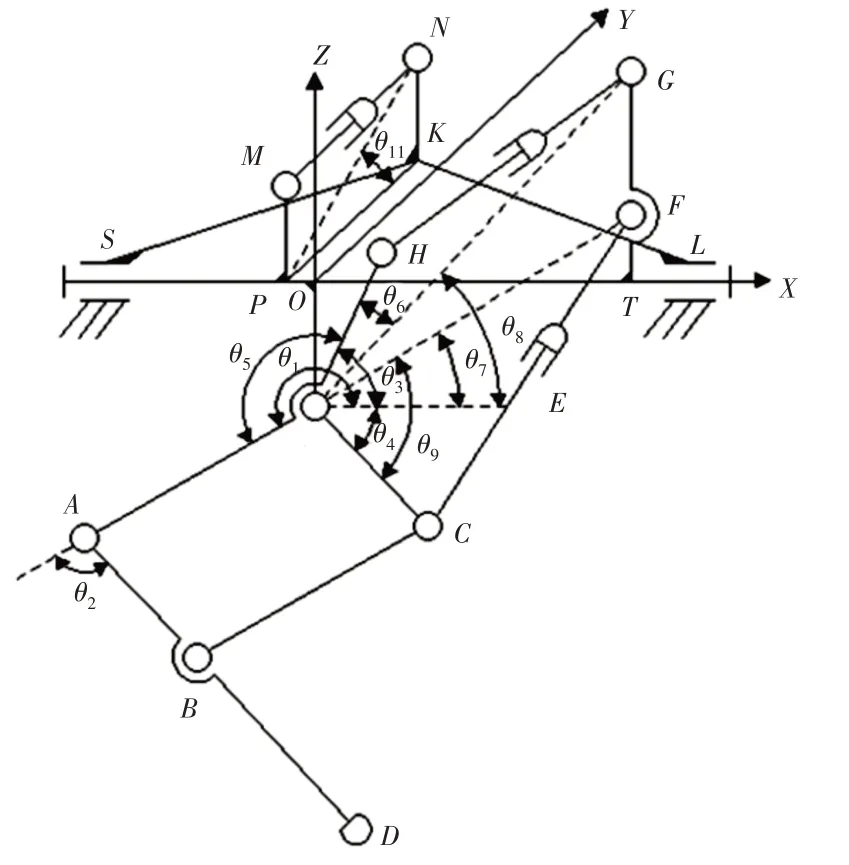
图3 机器人腿机构简图Fig.3 Schematic Diagram of Robot Leg Mechanism
并联机构绕X轴的旋转矩阵为:
式中:θ10—并联机构绕X轴的旋转角度,由几何关系可得:
3.2 运动学方程的建立
3.2.1 腿机构运动学正解分析
位置正解分析为已知驱动HG、CF、MN的长度,求解足端参考点D在坐标系O-XYZ中的位置。由于该腿部机构为串并混联机构,直接计算正解会比较复杂,因此将整个机构分开求解。首先设并联机构无侧摆运动,根据并联机构中HG与CF的驱动杆长求出足端D在XOZ平面内的位置,然后根据旋转矩阵R(X,θ10)求出足端D在空间坐标系O-XYZ下的位置。
首先分析并联机构无侧摆运动时,足端D在XOZ平面中的位置,依据闭环矢量约束方程得:
由式(3)可以得到并联机构无侧摆运动时足端D在XOZ平面内的位置:
其中:
根据式(1)、式(2)、式(4)得到末端参考点D在坐标系OXYZ内的位置为:
3.2.2 腿机构运动学反解分析
位置反解分析是已知足端D的坐标值,求解驱动l1、l2、l3的长度。根据式(7),当足端D在坐标系O-XYZ中的坐标值(XD,YD,ZD)已知时,可以解出θ1、θ2、θ10,再由式(2)、式(5)、式(6)即可求出驱动l1、l2、l3的长度。
具体各驱动杆长为:
3.3 腿机构工作空间求解
腿机构工作空间作为衡量机器人运动性能的重要指标,是后续足端轨迹步态参数的选定与腿机构虚拟样机仿真的基础。
在位置正解分析的基础上求解S串并混联机械腿的工作空间,初步设定的机器人腿部机构的结构参数为:a=140mm,b=270mm,c=400mm,d=100mm,e=420mm,f=450mm,h=130mm,i=330mm,j=100mm,θ5=140°,θ7=24°,θ8=30°,θ11=18°,三个驱动电缸的行程长度范围为:
综合式(3)~式(7),在满足腿机构几何约束关系的条件下,采用蒙特卡洛法在XOZ与YOZ平面内分别绘制了腿机构足端D在前进和侧摆运动时的工作空间点阵图,如图4、图5所示。从图4、图5中可以看出机器人足端有较大的运动空间,机械腿在XOZ平面和YOZ平面内均能达到步长为0.5m步高为0.3m的抬腿动作,满足机器人在前进和侧向移动时的运动要求。
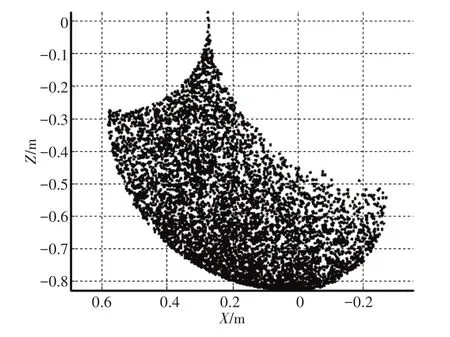
图4 XOZ平面点阵图Fig.4 XOZ Plane Lattice Diagram
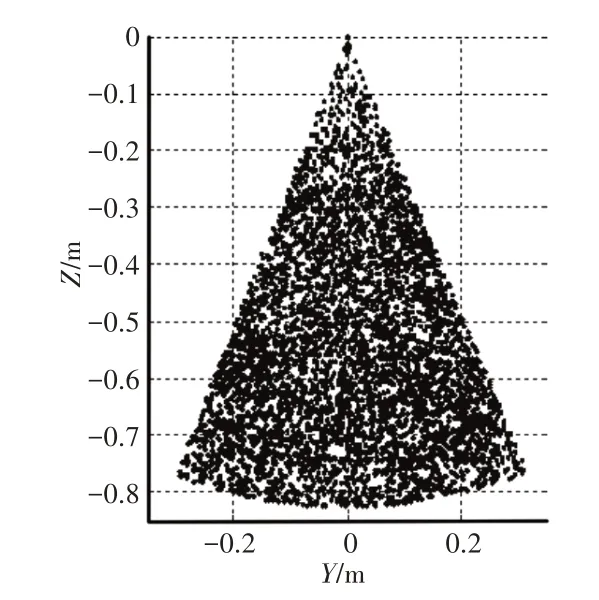
图5 YOZ平面点阵图Fig.5 YOZ Plane Lattice Diagram
3.4 腿机构速度雅克比求解
腿机构的速度雅克比矩阵作为机构输入速度与输出速度的影响系数,在机构运动学分析中起到重要作用。速度雅克比矩阵不仅反映了机构输入端与输出端的速度映射关系,还反映了机构运动灵活性及静平衡状态下操作空间力的线性传递关系。在位置正反解的基础上求解腿机构的速度雅克比矩阵,将式(7)对时间求导,得到足端参考点的三个速度分量如下:
分别将式(8)~式(10)对时间求导得到:
由腿机构几何关系可以得到:
综合式(11)~式(13)可以得到:
则腿机构的速度雅克比矩阵为:
4 仿真验证
为验证腿机构模型与理论分析的正确性,使用Adams软件对机器人的单腿模型进行运动学仿真。首先将机器人单腿的Solid‐works模型保存成Parasolid(*.x_t)格式,然后导入到Adams中,添加约束和驱动后,进行虚拟样机仿真,如图6所示。

图6 机器人单腿虚拟样机仿真模型Fig.6 Simulation Model of Robot′s Virtual Prototype with One Leg
为减少机器人足端在摆动相和支撑相切换时的惯性冲击力,本次仿真采用基于零冲击原则规划的足端轨迹[13],使机器人足端在触地时的速度和加速度为0,足端轨迹在水平方向和竖直方向的位移分量分别为:
令步长S=0.5m,步高H=0.3m,周期T=2s,其中,(0~1)s为摆动相,(0~2)s 为支撑相。为得到腿部三个驱动电缸的速度变化曲线,机械腿采用侧摆行走步伐进行仿真,仿真得到机器人单腿在一个运动周期内各驱动电缸的速度仿真变化曲线,如图7所示。
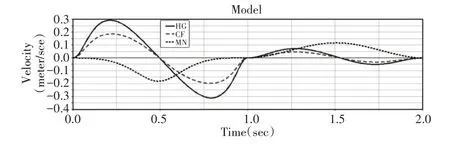
图7 腿机构驱动速度仿真曲线Fig.7 Simulation Curve of Driving Speed of Leg Mechanism
根据位置正反解和速度雅克比矩阵,使用Matlab计算得到各驱动电缸的速度理论变化曲线,如图8所示。
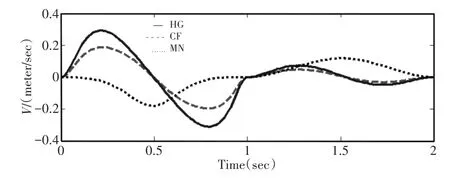
图8 腿机构驱动速度理论计算曲线Fig.8 Theoretical Calculation Curve of Driving Speed of Leg Mechanism
最后将Adams仿真结果与Matlab理论计算结果进行对比,得到速度误差变化曲线,如图9所示。从图9中可以看出,仿真数据与理论计算数据误差保持在(±1×10-3)m/s内,误差值较小,存在误差是因为模型导入以及软件计算精度之间存在一定偏差。由此验证了运动学模型的正确性。
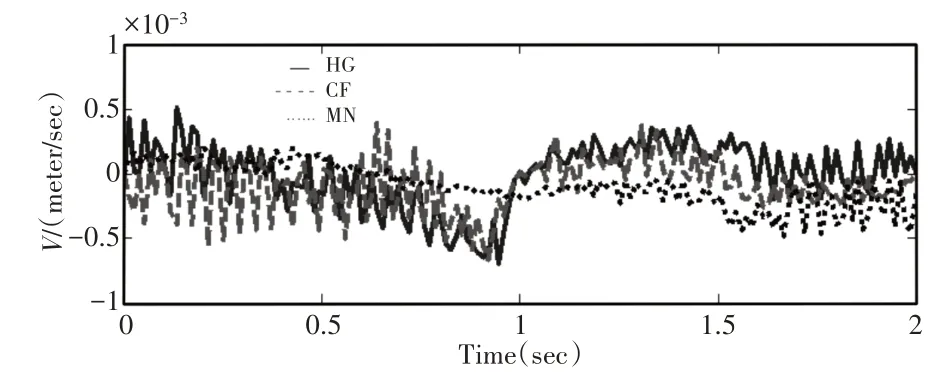
图9 驱动速度误差变化曲线Fig.9 Variation Curve of Driving Speed Error
5 结论
提出了一种适用于仿生四足机器人的新型串并混联腿部机构,建立了仿生四足机器人三维模型。在三维建模的基础上对机器人腿部进行了运动学分析,推到了串并混联结构的位置正反解,并求出了反映腿机构输入端与输出端速度线性关系的雅克比矩阵。在位置正解的基础上,使用蒙特卡洛法求解了机器人足端的工作空间,求解结果显示足端的运动空间较大,在前进和侧摆方向均能达到步长为0.5m、步高为0.3m的抬腿动作,满足机器人腿部的行走要求,为运动仿真提供了理论依据。在机器人腿部工作空间范围内,引入基于零冲击原则规划的足端轨迹,对机器人单腿模型进行了虚拟样机仿真,得到驱动速度变化的仿真曲线,并与理论计算曲线进行比较,得到了仿真值与理论计算值的误差曲线,误差曲线显示各驱动电缸的速度误差保持在±1×10-3m/s范围内,误差值较小,验证了腿机构运动学模型的正确性,为腿部机构的静力学分析和动力学分析及整机结构优化奠定了基础。

