改进RRT算法的无人驾驶车辆路径规划研究

樵永锋，王瀚鑫，周淑文，杨贵军

（1.东北大学机械工程与自动化学院，辽宁 沈阳 110819；2.丹东东方测控技术股份有限公司，辽宁 丹东 118002）

1 引言

随着人工智能领域的兴起，无人驾驶车辆已经成为未来汽车工业的发展趋势，无人驾驶技术［1］也随之成为当下最热门的研究方向。其中，路径规划［2-3］作为无人驾驶的关键技术之一，引起了行业的广泛关注。路径规划是无人驾驶车辆从行驶空间中获取一条满足自车约束条件的无碰撞可行路径，而安全性，平稳性，高效性则是衡量无人驾驶车辆已规划路径是否最优的重要指标。

在基于采样的规划算法中，快速扩展随机树（RRT）因其算法具有概率完备，适用性强等扩展特性而被广泛的研究和应用。然而基础RRT算法也存在一些明显的不足之处：路径搜索过程中节点盲目扩展，无指向性，再现性差，路径曲折波动性大，收敛速度不稳定，通过狭窄区域时，搜索效率降低。目前，已有一些国内外学者提出了针对性的衍生算法［4-5］来解决上述问题。文献［6］提出了RRT*算法，实现了采样空间的约束，解决了路径非概率最优的问题；文献［7］提出了B-RRT*算法，采用起始点和目标点的双向扩展的策略，进一步提高了算法的收敛速度；文献［8］提出了基于连续曲率的RRT算法，引入自车和环境约束，有效提高了路径质量；文献［9］提出了基于采样点高斯分布的RRT算法，建立期望路径模型，降低算法随机性；文献［10］提出了基于引导域的改进算法，使RRT算法的扩展过程在A*算法生成引导域中进行，减少RRT算法的盲目性；文献［11］提出了PI-RRT*算法利用人工势场法结合启发集合采样的最优路径收敛方法，提高了最优路径生成速度。

上述提及的算法在路径质量，搜索效率等方面实现了优化，但经上述优化后得到的路径并不适用于无人驾驶车辆追踪行驶。为使规划后的路径符合实际驾驶工况，满足车辆行驶要求，在传统RRT算法的基础上提出一种改进算法，以启发式采样替代随机采样策略，引导路径向目标点方向扩展，设置转角阈值约束转角范围，减少无效节点的生成，同时结合自适应权重分配的局部扩展方式，避免陷入局部最小值，然后以变步长的扩展方式，提高算法局部避障绕障能力，最后提出节点优化策略，并基于3次B样条曲线和Reeds-Shepp曲线进行路径后处理，实现路径长度优化并解决了路径平滑和终点航向问题。

2 车辆运动学模型

车辆运动学是从几何学的角度展开车辆运动的研究，包括行驶空间中的速度和位置等变量随着时间而产生的相应的变化。在路径规划算法中考虑车辆的运动学模型，可以使得规划得到的路径可行性更高，并且能够保证行驶过程中自车的运动学约束，这里采用的车辆运动学模型是单车模型，如图1所示。单车模型是基于阿克曼转向模型的简化，将左右两侧车轮简化合并为一个，只考虑车辆在惯性坐标系XOY下运动，可得简化的车辆运动学方程如下：

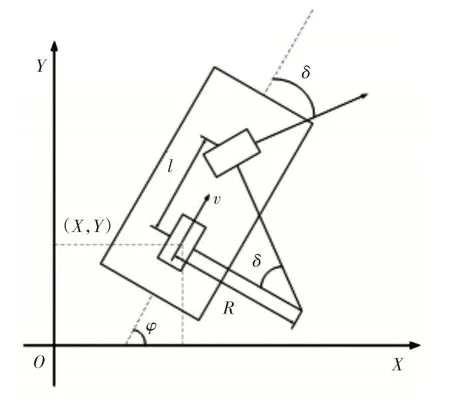
图1 运动学模型Fig.1 Kinematic Model

式中：(X，Y)—后轴轴心坐标为(X，Y)；v—后轴轴心速度；φ—车辆横摆角；δ—车辆前轮等效转角；l—轴距。

根据前轮等效转角与后轴遵循的曲率半径之间的几何关系，可得下式：

式中：R—后轴曲率半径。曲率的定义为：

实际上，车辆转向过程是曲率连续的弧线，且有最大曲率的约束。由式（3）可知，车辆的转角与路径曲率相关，这为下文改进算法提供优化思路：通过车辆相关参数，车辆的转角与路径曲率相关，引入转角约束优化路径曲率，实现路径曲率最优，达到将车辆运动学与规划算法结合的目的，让规划后的路径更易于车辆追踪，提高可行性。

3 RRT算法及其衍生算法介绍

3.1 RRT算法

基础RRT算法的原理，如图2所示。将起始点作为根节点，在所在环境区域内生成一个随机点，然后寻找随机树中与该随机点距离最近的树节点作为父节点，沿着父节点到随机点的方向扩展单位步长形成子节点，为搜索的新节点。扩展过程无障碍碰撞，则此次扩展成功，子节点加入随机树集合中；若发生碰撞，则扩展失败，重新生成新的随机点。扩展成功后，判断子节点是否进入目标点区域，若未达到重复上述搜索过程直至寻找到目标点。

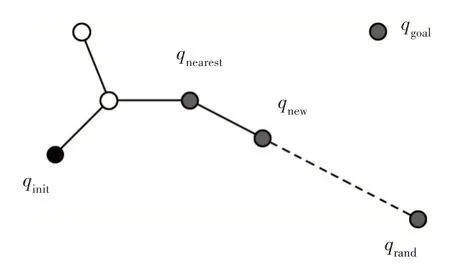
图2 基础RRT算法扩展示意图Fig.2 Extension of the Basic RRT

3.2 RRT＊算法

RRT*算法在RRT算法基础上，增加了父节点重选和随机树重新布线两个计算过程。每次迭代生成新节点后，在以新节点为中心，定义长度为半径的圆形范围内搜索的临界节点，作为潜在的父节点，计算起始点经过临近点到新节点的代价，若出现比当前路径代价更低的新路径，则进行父节点替换，删除原路径，完成父节点的重选过程。接着，进行随机树重新布线过程，检查临近点，若存在起始点经过新节点再到临近节点的代价小于其现存路径的代价，则该临近点将以新节点为父节点，进行路径更换。具体算法流程如下：

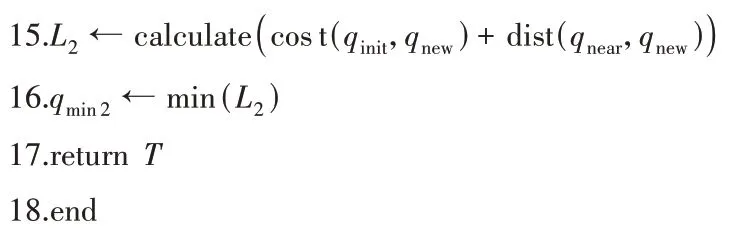
RRT*算法的核心思想是减少路径代价，相比于基础RRT算法，具备了渐进优化的特性，即随迭代次数的增加，路径质量逐步优化，达到最优收敛的目的。

3.3 Informed RRT＊算法

Informed RRT*算法［12］是对RRT*算法的采样策略进行改进。RRT*算法沿用RRT算法的随机采样策略，在环境空间内均匀采样，Informed RRT*算法则是先得到一个初始路径，根据初始路径将整个采样区域收缩成椭圆区域，并且随着节点不断地扩展，椭圆的区域不断缩小，以限制采样区域的方式提高随机树的扩展效率。椭圆采样区域C定义是在环境空间为Qfree下，以起始点qinit和目标点qgoal作为椭圆的两个焦点，初始路径为σbest，起始点与目标点距离为σmin：

在每次迭代优化路径后，都会出现一条新路径，若新路径的长度更短，则以该路径长度作为新的σbest，更新椭圆采样区域，过程如图3所示。

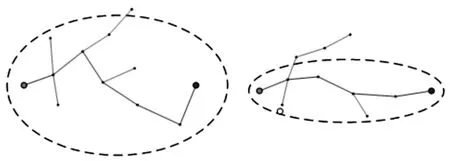
图3 椭圆采样区域更新Fig.3 Update of Ellipse Sampling Area

Informed RRT*算法是对已得路径的优化，将优化范围限制在椭圆区域内，从而减少随机树冗余的分支，提高路径质量，实现路径长度最优。

4 算法改进策略

4.1 障碍检测策略

由于实际驾驶环境中会存在各种特殊的场景如狭小空间，多障碍物场景等，随机采样点落在障碍物附近，会引领无人车向障碍物方向行驶，这是具有巨大危险隐患的，仅仅通过基础RRT算法的避障特性是远远不够的，因此需要更为严谨的障碍物检测策略，提高路径可行性。

基础算法将采样节点视为质点，并未考虑车辆本身的大小，但在实际驾驶过程中障碍物及车辆均为具有几何参数的形体，若不加以考虑，车辆在跟踪路径时有与障碍物碰撞的风险。因此为了满足避障要求，如图4所示。对节点进行膨胀处理，并构建障碍物检测圆。

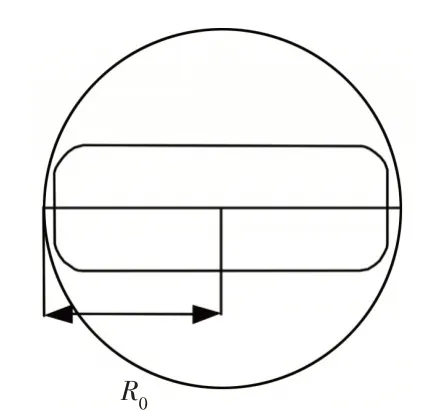
图4 节点膨胀处理Fig.4 Expansion of Node

节点膨胀定义为，以无人车中心(x0)，y0为圆心，R0为半径进行膨胀，得到方程为：

式中：R0—车身长度L的一半。

障碍物检测圆的定义是，将膨胀后的圆形区域进行以一定的比例系数λ进行检测区域放大：

改进算法分别以λ=4，λ=8构建两类障碍物检测圆，引入此策略能够实现大范围的障碍物检测，并保证车辆在足够充裕的空间内进行有效避障。

4.2 启发式采样策略

4.2.1 基于权重分配的目标指向性采样

基础RRT算法是以环境地图随机采样的方式，在随机点会出现盲目扩展的情况，会导致无效节点的生成，无法进行有目的性的搜索扩展，忽视局部路径细节变化，导致无效规划时间增加，这大大降低算法的搜索效率。引入目标指向性采样策略实现采样过程的优化，目标指向性采样策略定义为：

算法初始化的时候预设一个指向概率数P0，然后在每个迭代周期生成随机点之后，生成一个随机概率数Prand，然后进行概率数大小判别，若Prand>P0，目标点为此次扩展的随机点；若Prand≤P0，随机点保持不变。

虽然引入指向性的采样方式，给节点扩展提供一个指引方向，减少随机树向其他方向无效扩展，但由于改变的采样概率分布，无法保证避障特性和指向特性同时处于可控范围之内，易出现陷入局部最小值，无法收敛的情况。解决思路为借助上文障碍检测函数，进行障碍物检测，若障碍物检测圆中无障碍物执行原有指向性采样策略；若出现障碍物，则采用权重分配的目标指向性采样，如图5所示。

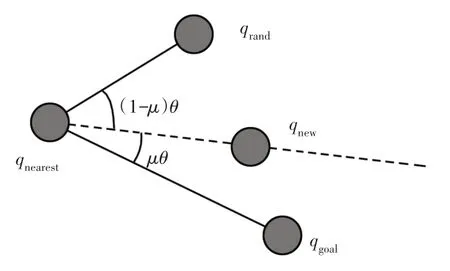
图5 权重分配策略Fig.5 Method for Weight Distribution

基于权重分配的目标指向性采样，当Prand≤P0时，qnew可表示为：

当Prand>P0时，qnew表示为：

式中：μ—权重分配系数；ρ—扩展步长。

4.2.2 变步长策略

基础RRT算法中采用固定步长进行新节点的扩展，当通过狭窄区域和多障碍物环境时，其避障绕障能力下降，搜索效率大幅度下降。这里通过变步长策略，结合障碍检测策略，获悉障碍物与路径相对位置，执行相应的步长进行节点扩展，充分利用地图信息，提高算法局部避障能力，变步长依据与障碍物相对位置将步长分为大，中，小三类步长，当一类障碍检测圆中无障碍物，无人车与障碍物距离较远，采用大步长进行扩展；当障碍物处于两类障碍圆之间时，采用中步长进行扩展；当父节点与障碍物距离小于二类障碍物检测圆半径时，采用小步长进行扩展：

式中：d—父节点与障碍物的最短距离；d1—第一类障碍物检测圆半径；d2—第二类障碍物检测圆半径。其中，扩展步长与障碍物始终保有一定的安全距离ds≥2R0。

4.2.3 节点转角阈值

正常情况下车辆在行驶过程中，由于车辆自身的非完整性约束，其转向角度在相对较小的范围内平稳变化，不会出现过大转角的情况，基础RRT算法在节点随机扩展的过程没有考虑无人车的自身非完整性约束，故设定节点转角阈值，限制转角范围，更适用于无人车辆行驶。具体选取策略，如图6所示。

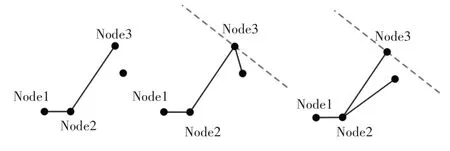
图6 节点转角阈值选取策略Fig.6 Node Corner Threshold Selection Strategy

由图6 可知，随机点Node1 距离Node3 距离最近，但其超过了节点转角阈值，这里并不将随机点舍弃，生成新节点，而是采用舍弃最近节点，重新进行最短距离判断，选择距离稍远一些，但在转角阈值范围的节点Node2 作为次近点，这样会避免由于节点转角阈值的约束舍弃节点，导致随机采样数的增加的情况，提高算法效率。

4.2.4 父节点重置

改进算法在RRT*算法父节点重选过程的基础上进一步改进，在增加新节点与目标点的距离代价值，并引入调节系数进行临近=节点总代价的计算。总代价的计算公式为：

式中：Ct—总代价；ω1，ω2，ω3—调节系数；Cin—起始点到临近节点的代价值；Lnn—各临近节点到新节点的欧氏距离；Cng—新节点到目标点的预估代价值。

将改进后总代价最低的临界节点作为替换的父节点，实现启发式的节点扩展过程，提高路径质量，减少收敛时间。

4.3 后处理

4.3.1 节点优化策略

改进算法引入启发式采样策略后，搜索效率得到了明显的提升，但搜索得到的路径仍会出现无效的分支路径，局部范围内出现路径波动，造成路线冗余，出现绕远的情况，使得路径长度并未实现最优，因此需要对路径进行节点优化，去除多余节点，优化路径长度。核心策略为：引用贪婪算法的思想，对原有路径的节点进行择优判定，首先将起始点qinit加入新路径节点集合中，并将qinit作为判定起点，判断与起始点qinit连线上是否存在障碍，若无障碍则进行下一节点的判定，直至出现节点qi与起始点qinit连线存在障碍，将qi加入新路径节点集合，并作为新的起点重复上述择优判定过程，直至遍历全部原有节点，最终得到新路径节点集合，即为节点优化后的新路径，将冗余节点去除，实现路径长度的优化。

4.3.2 路径平滑处理

经节点优化后的路径，实现路径长度最优的目标，但得到的路径仍为连续折线，不够平滑，曲率并不连续，车辆在跟踪该路径时，航向角会发生突变，严重影响车辆平顺性和安全性，故对路径进行平滑处理，才能得到真正满足车辆跟踪要求的最佳路径。这里采用三次B样条曲线对路径进行平滑性拟合处理，如图7所示。

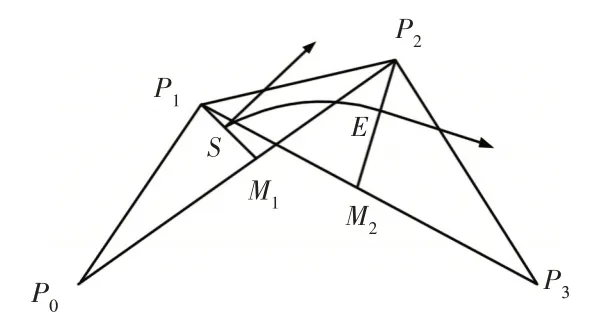
图7 三次B样条曲线Fig.7 Cubic B-Spline Fitting

三次B样条曲线的阶次决定了平滑后曲线具备三阶次连续性，三阶连续的平滑路径贴合真实驾驶场景，进一步满足车辆追踪。B样条的表达式为：

式中：Pi+k(i=0，1，...，m，k=0，1，...，n)—控制点；n—基函数的次数；Fk，n(t)—n次B 样条基函数，也称为样条分段混合函数，定义为：

应用上述公式，控制点由RRT算法中的路径节点代替，设定三次B样条曲线公式：

三次B样条的拟合曲线为：

4.3.3 目标点航向约束

对于无人驾驶车辆而言，目标点通常为工作区域，停车位等场景，存在倒车等工况，故对车辆在抵达目标点时的航向有一定的要求，为了使规划的路径能够结合实际停车位姿的航向信息，对目标点区域进行航向约束。改进算法采用Reeds-Shepp曲线进行路径末端的节点连接，解决目标点航向问题。

Reeds-Shepp 曲线同时满足起始位姿和终止位姿的最短路径。考虑车辆倒车的情况，可实现任意位姿抵达目标点，保证无人驾驶车辆抵达终点时最终的航向角度，并且曲线由半径固定的圆弧和直线组合的特性也能够满足车辆最小转弯半径的要求。Reeds-Shepp 曲线可以描述的路径类型分为9 种：C|C|C，CC|C，C|CC，CSC，CCβ|CβC，C|CβCβ|C，C|Cπ2SC，CSCπ2|C，C|Cπ2SCπ2|C。其中，C表示转向，S表示直行，“|”表示正反向的转换，下角标表示转向角度。

目标点航向约束是在目标点为圆心，ε为半径构建圆形区域，获得路径与区域交点qi的位姿信(xs，ys，φs)，根据实际情况给定目标位姿信息，利用Reeds-Shepp曲线进行交点与目标点的连接，实现车辆的最终位姿要求，并兼具曲率的连续性。

5 仿真分析

为了验证改进算法的优越性能，分别对基础RRT 算法，RRT*算法，Informed RRT*算法及改进算法四种算法分别在简单障碍场景，狭窄通道场景，复杂障碍场景等环境下进行仿真验证，对所得规划路径进行对比分析，三种场景目标点航向角分别设置为π/2，π，3π/4，以验证目标点航向约束的普遍适用性，不同算法中的主要参数与仿真场景均保持一致。改进算法仿真相关参数，如表1所示。仿真结果对比，如图8～图10所示。

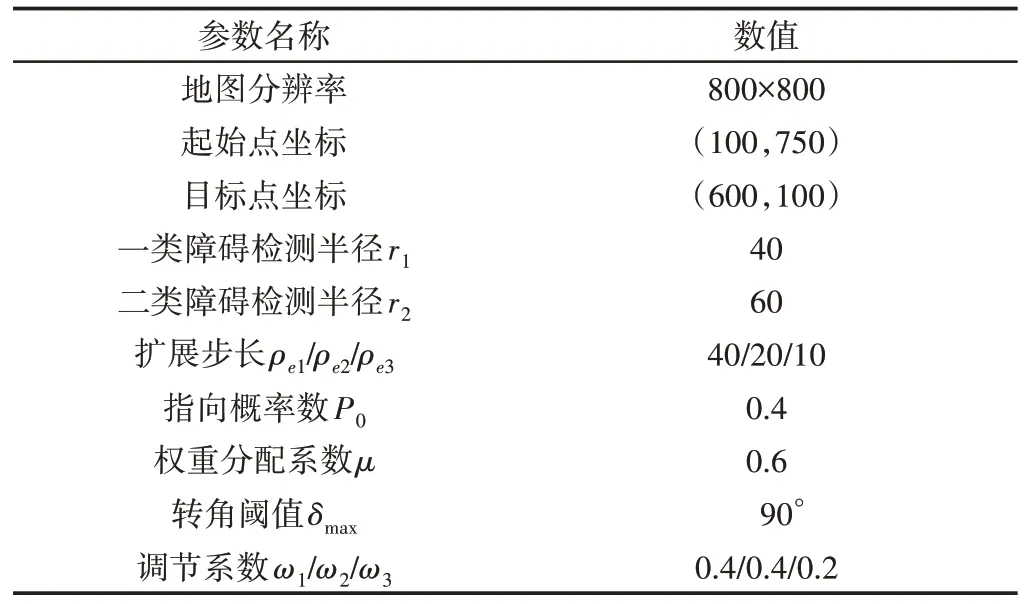
表1 仿真所用主要参数Tab.1 The Main Parameters of Simulation Used

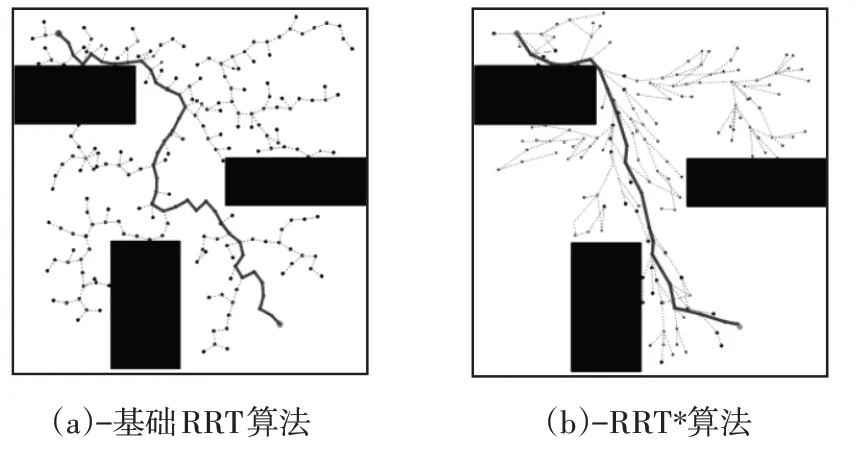
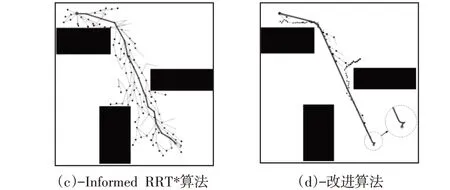
图8 简单障碍场景中仿真结果对比Fig.8 Comparison of Simulation Results in Simple Obstacle Scenario

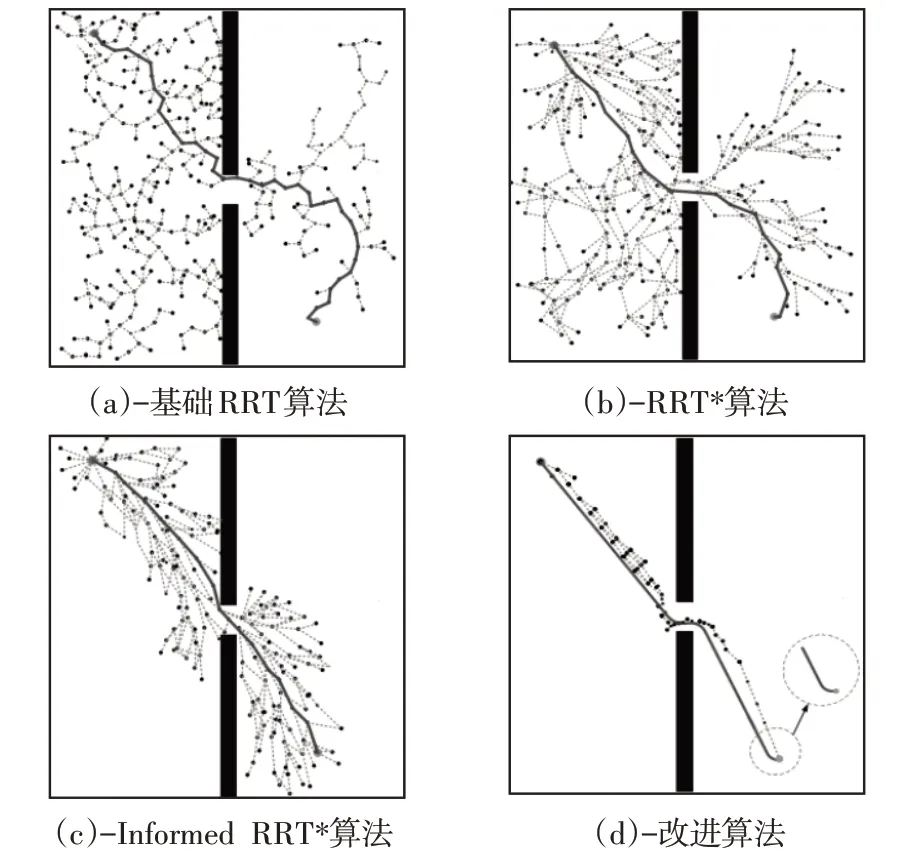
图9 狭窄通道场景中仿真结果对比Fig.9 Comparison of Simulation Results in Narrow Channel Scenario

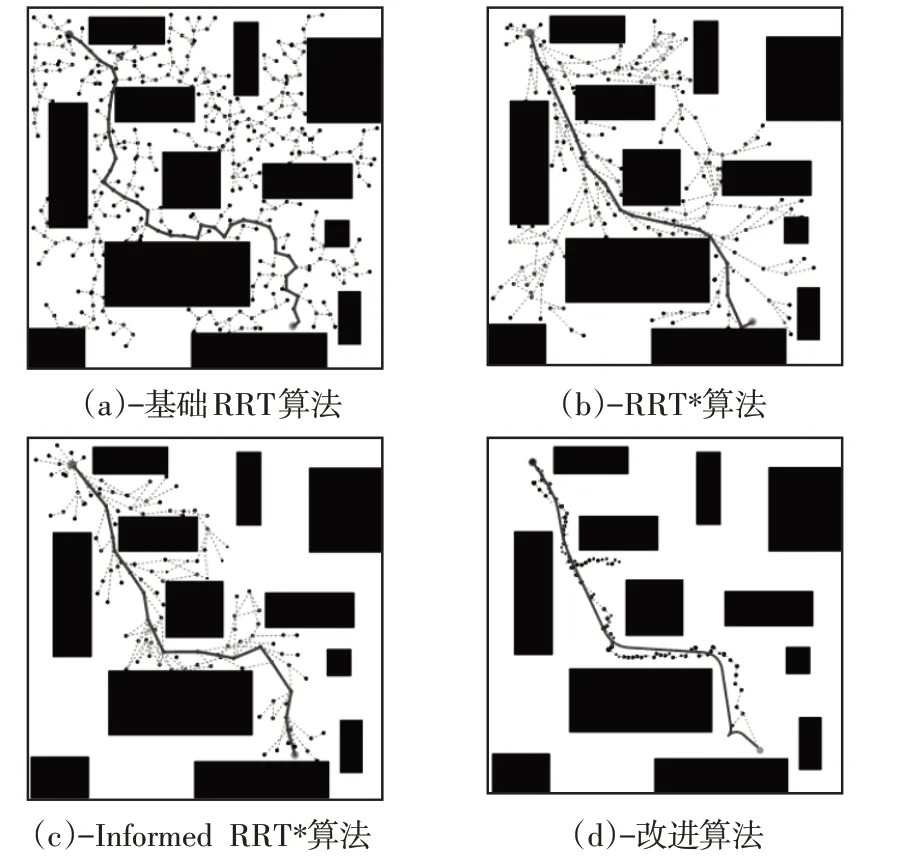
图10 复杂障碍场景中仿真结果对比Fig.10 Comparison of Simulation Results in Complex Obstacle Scenario

由图8～图10仿真结果进行对比可知算法的改进之处：冗余节点大量减少，避障绕障能力得到提升，通过狭窄区域能力提升，实现环境信息利用的最大化，大大提高了算法的规划效率，得到路径长度实现最优并兼具平滑性，符合车辆追踪要求，并能解决目标点的车辆航向问题，且具有普遍适用性。由于算法的随机性，每种场景进行100次路径规划仿真实例，对4种算法得到的仿真结果进行统计，其中，各个指标结果均为平均数值，仿真实例数据，如表2～表4所示。

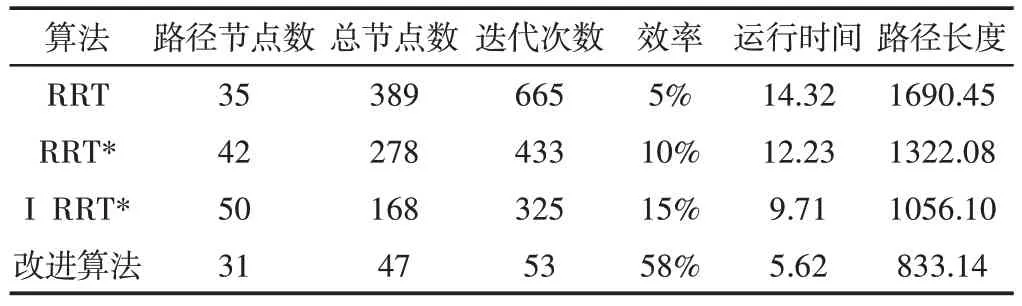
表2 简单障碍场景仿真数据Tab.2 Simulation Data in Simple Obstacle Scenario

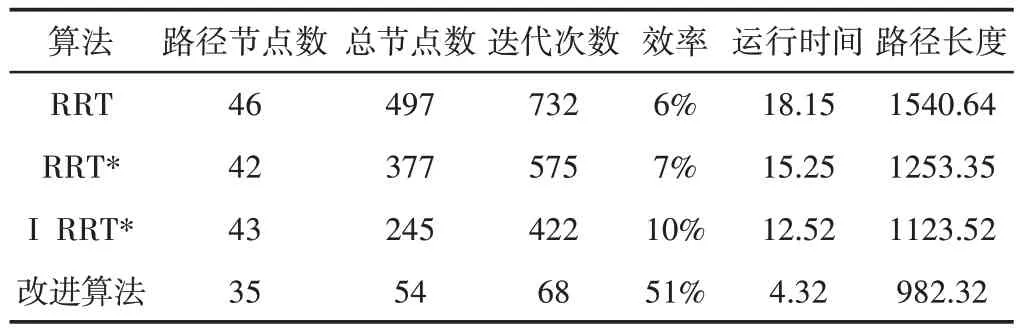
表3 狭窄通道场景仿真数据Tab.3 Simulation Data in Narrow Channel Scenario

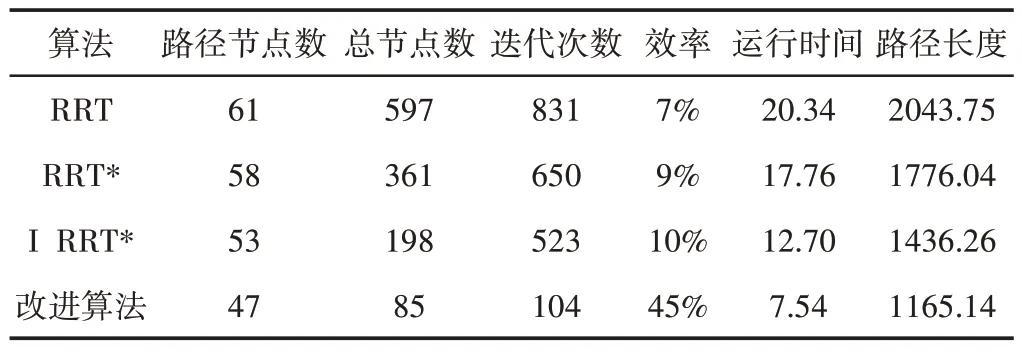
表4 复杂障碍场景仿真数据Tab.4 Simulation Data in Complex Obstacle Scenario

根据表2～表4，将简单障碍物场景，狭窄通道场景，复杂障碍物场景三种场景下仿真实例数据综合分析可知，改进算法平均扩展节点数为62个，相较于RRT及其衍生算法，平均扩展节点总数分别减少了87.45%，81.71%，69.61%；改进算法平均迭代次数为75，分别减少了89.91%，86.44%，82.67%；三种场景下改进算法节点利用效率均实现了提升，分别是58%，41%，45%；平均规划时间为5.83s，缩短了66.89%，61.34%，49.94%；平均路径长度为993.53mm，减少了43.49%，37.98%，31.81%。由此可知，改进算法在各项指标上都实现了明显的提升。以简单障碍场景为例，提取四种算法所得路径，其具体曲率变化情况，如图11所示。图中横轴表示路径当前位置占总路径的百分比（简称为路径百分比），纵轴为曲率的绝对值。通过对比可以发现，基础RRT算法及其衍生算法所得路径的曲率突变情况明显，改进后的算法所得路径曲率连续且平滑，且曲率最大值为0.047，满足车辆最大曲率要求，从而保证了车辆追踪规划路径过程时的平稳性和安全性，相比之下，验证了改进算法规划路径平滑程度的优越性。

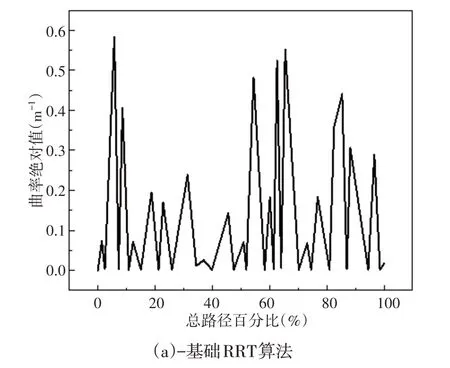
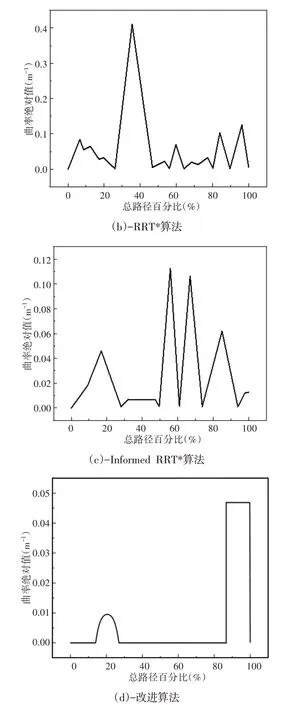
图11 曲率变化Fig.11 Change of Curvature

6 结论

（1）在RRT 算法的基础上，设计了启发式的采样策略，包括基于权重分配的指向性采样，变步长扩展，转角阈值约束等策略，并对规划路径进行后处理，分别采用节点优化策略，三次B样条曲线进行平滑处理，Reed-Shepp曲线进行目标点的连接，有效地解决了路径长度，平滑性及目标点航向问题。改进后的算法大幅度提高了搜索效率，总节点数减少了约80%，规划时间缩短了约60%，路径长度减少了约40%，满足平滑性要求及车辆最大曲率要求全方面提高了路径质量。（2）利用Matlab软件进行三种工况下的仿真实例验证，分析了仿真数据，验证了改进后算法的有效性和优越性，具备普遍性和准确性。