考虑时空特征的机器人VRP问题求解方法

张 炜，宾冬梅，梁俊斌

（1.广西电网有限责任公司电力科学研究院，广西 南宁 530023；2.广西大学广西多媒体通信与网络技术重点实验室，广西 南宁 530004）

1 引言

变电站巡检的项目、周期、方式及要求均有明确规范，是电力生产中的常规工作，也是占据运行人员精力的主要工作。近年来，变电站巡检机器人已在电力行业推广运用，并深刻改变了设备巡检模式［1-2］。变电站机器人巡检系统由变电站机器人、本地监控后台、远程集控后台、机器人室等组成，能够通过全自主或遥控模式开展变电站的红外热成像、可见光、噪声等检测作业，提高工作效率和质量，缓解结构性缺员等问题［3-4］。其中，变电站机器人由移动载体、通信设备和检测设备等组成的，采用遥控或全自主运行模式，用于变电站设备巡检作业的移动巡检装置。

变电站巡检机器人管理模式分为集控管理和分布管理。随着机器人铺开推广，电网企业纷纷建设了远程集控后台，并研究应用了可集中调配管理辖区内机器人的集控管理模式［5-6］。集控管理模式的优势在于可以在不同变电站之间调配机器人资源，充分应用数量有限的机器人。在此前提下，考虑多机器人、多起点、多时间窗等组合优化条件的转移运用车辆路径问题（Vehicle Routing Problem，VRP），成为提升机器人整体调配效率的关键。此类问题是基于单台机器人路径规划问题的延伸应用，但是问题求解难度随参与调配机器人的数量不同而呈指数级增长［7］。

VRP问题具备典型的时空分布特征，其应用研究不局限于交通运输方面，且已拓展至电网布局等方面［8］。变电站机器人VRP的优化目标是指在遍历巡检不同变电站过程中，给出一组总行程最短的调度方案集合［8］。当前变电站机器人路径规划方面的研究工作仅侧重于机器人在站内行走的路径长短、安全避障及动作难度［9-11］，缺少机器人在变电站之间转移运用的路径规划研究。同时，简单依靠人工经验决策、基于排队论的传统静态问题等物流算法，又容易陷入局部最优、过程复杂等局限［12-13］。论文针对机器人群体的互动时空特征，考虑以巡维中心、变电站为节点构成的点线网络，提出针对机器人群体调度分配过程中VRP问题的路径规划算法，得到开放式的路径方案。

2 VRP问题描述

2.1 设备巡检

变电站巡检包括日巡、夜巡，通常有人值班站日巡每日一次，夜巡每周一次；无人值班站日巡、夜巡每月一次。特殊情况时，将灵活调整巡检项目、周期、次数等。变电站机器人可针对14类设备，执行74项巡检任务。因为变电站的分布位置、设备数量、场地规模不同，所以机器人的巡检区域、任务点及耗时等也存在差异［14］。解决调配巡检机器人路径规划的VRP问题，需综合考虑巡检机器人电量、路途耗时、巡检周期、停留充电等因素。

2.2 路径规划

路径规划是指搜索空间网络中位置之间最小成本函数的路径［15］。路径规划技术在机器人自主运行、无人机避障飞行、城市道路网规划、物流交通管理等领域应用广泛，有助于分析解决拓扑为点线网络的规划问题［16］。调度分配变电站机器人是电网企业制定电力生产周期性巡检计划的内容，同样面临着机器人群体路径规划的VRP问题。

调配单台变电站机器人是指在已知变电站节点位置、路径参数等拓扑网络布局及巡检项目情况下，机器人个体以最短路径巡检全部变电站。调度分配多台变电站机器人，则可以理解为求解机器人群体的最优路径组合，但最优路径目标难以协调一致。

调度分配多台变电站机器人的VRP问题可以描述为：多台巡检机器人从属的不同巡维中心出发，赴不同变电站巡检，在不浪费工作时间（充电、巡视、途中及回传数据）的前提下，以最短路径遍历巡检既定的变电站。当前主要依靠人工经验决策、基于排队论的传统静态问题物流算法制定调配变电站机器人的路径策略［17-18］，未能基于时间及空间特性研究运行规则，故难以实现对机器人群体路径规划所需的全局最优。

3 机器人调度分配算法

3.1 基于时空三维坐标系的路径规划

在调配单台变电站机器人个体时，仅需基于遍历式寻优思路提出路径最短的巡检方案，属于“一对多”的路径规划。但在调度分配多台变电站机器人群体时，还需考虑机器人所在的不同位置，进而提出组合优化后的路径规划。机器人群体调度分配受到机器人当前部署位置、变电站分布位置及工作时间等时空限制条件。论文以变电站的横、纵坐标为第一维和第二维，以时间为第三维，建立“时间-空间”分析框架，并基于时空三维坐标系中提出机器人的“时空路径”，求解VRP问题。首先建立基于变电站位置构建平面二维坐标的宏观路网；其次梳理距离、能耗等约束条件，构建考虑时间窗的时空三维坐标系；最后遍历搜索各机器人的可选路径，并提出解决VRP的调配方案。考虑时间窗的时空三维坐标系有助于满足时空约束条件，得到最优路径规划［19-20］。

3.2 路径规划的约束条件

调度分配变电站机器人群体的VRP问题需面对路径规划过程中的时限和距离这两项约束条件。

一方面，时限约束是指机器人完成站内巡检任务所需的工作时间，但是由于变电站的设备数量、场地规模不同，导致机器人所需工作时间各不相同，即时间窗存在差异［14］，并成为与传统VRP问题解决方案的主要区别。另一方面，距离约束是指机器人全部巡检一轮变电站所需转运的路径最短。

为求解机器人群体路径规划的最优组合，透过基于时间窗的时空三维坐标系分别处理机器人个体的转运路径，即可避免陷入局部最优和繁复计算。

3.3 群体路径规划算法

调度分配机器人群体算法采用启发式原理，可在路径规划过程中逐步收敛至全局最优解，算法基本流程，如图1所示。

图1 路径规划算法Fig.1 The Algorithm of Path Planning

（1）输入待巡检变电站、机器人所属巡维中心的数量、坐标及巡检所需时间窗，构建基于时间窗的时空三维坐标系，并设置迭代次数为N以及迭代次数最大值Nmax；其中巡维中心的数量为A；

（2）将m台机器人随机均匀地部署在A个巡维中心，初始化机器人k已巡检的站点集Ck以及待巡检站点集；初始设置已完成巡检任务的机器人数量l=0；

同时，设置巡维中心数量的最大值Amax，设置机器人的总数量的最小值mmin，其中，每个巡维中心配置（1～3）台机器人，即mmin≥Amax。例如，Amax为100，即巡维中心实际最大值为100，可设置的mmin为100。

（3）当机器人k电量至少满足巡检一座目标站点时，则将机器人k转运至目标站点j，并更新机器人k已巡检的站点集Ck以及待巡检站点集；

同时，m台机器人随机选择一座变电站为始发站点，机器人k由站点i出发至下一目标站点j，并由转运概率遴选转运路径，转运概率的计算方式如下：

（4）如果待巡检站点集≠∅，至少有一个待巡检站点的任务量满足机器人k当前电量，则转（3）；否则转（5）；

（5）如果待巡检站点集≠∅，机器人k当前电量不满足完成剩余待巡检站点的任务量，则在当前站点充电，使其恢复充足的电量，并转（3）；否则，转（6）；

（6）如果待巡检站点集≠∅，并且机器人k当前最后剩余的巡检站点附近不是巡维中心班部所在站点，则令其返回至最近的巡维中心；如果已完成巡检任务的机器人数量小于机器人的总数量，即l＜m，转（3）；否则，转（7）；

（7）所有机器人完成既定巡检任务后，则更新其电量需求，具体如下：

当所有机器人完成一次重复转运计算迭代后，各边上的节点电量需求由以下公式更新：

式中：ρ—电量需求中的测算因子；

Δτij—边（i，j）上的电量需求变化量；

Δτijk—第k台机器人在边（i，j）上的电量需求量；

Q—机器人完成一次转运所释放的电量需求总量；

Lk—机器人所经过的路径距离。

（8）由已巡检的变电站节点集Ck得到m台机器人的路径集L=｛L1，L2…Lm｝，根据（3）～（6）计算并记录本次迭代得到的最优路径集，同时更新全局的最优解；

（9）迭代计算，如果同一最优解连续出现m次，则转（10），否则转（11）；

（10）分别向m台机器人输出方案；

赭曲霉毒素A（OTA）是由多种生长在粮食（小麦、玉米、大麦、燕麦、黑麦、大米等）、蔬菜等农作物上的曲霉和青霉产生的[1-3]。目前，小麦、大麦、玉米等谷类作物中OTA的测定方法有薄层色谱法（TLC）、酶联免疫吸附法（ELISA）[2-7]、高效液相色谱法（HPLC）[3]和胶体金免疫快速定量检测法（GICT）[4]。本研究对常用的三种检测方法即HPLC、ELISA和GICT进行了考察，从仪器、人员和时间等多方面论证了三种检测方法的优劣，从最低检出限、定量限、回收率、精密度和重复性等参数分析了三种检测方法的精确度，为日益复杂的检测需求提供了多种选择[8-11]。

（11）如果迭代次数达到Nmax，但仍未连续出现m次最优解，则停止迭代计算，并向运维决策人员提出手动配置建议。

4 算例分析

某供电局的3台机器人分布在3个巡维中心，需外出完成12座户外式无人变电站的日巡工作。机器人充电后工作时长不小于9h。给定待巡检站点的名称、相对坐标、数量、时间窗，如表1所示。

表1 时间窗约束条件Tab.1 The Constraints of Time Windows

根据表1所示内容，绘制机器人在巡维中心、各站点之间的群体互动时空分布图，如图2所示。

利用群体互动时空分布图，算法寻找潜在的下一时空节点，就简化为机器人在各站点相对坐标、时间圆柱的交集。图2中的X轴、Y轴构成平面二维坐标，表示巡维中心和变电站的空间位置；垂直坐标（T轴）上的时间圆柱表示完成巡检所需时间。

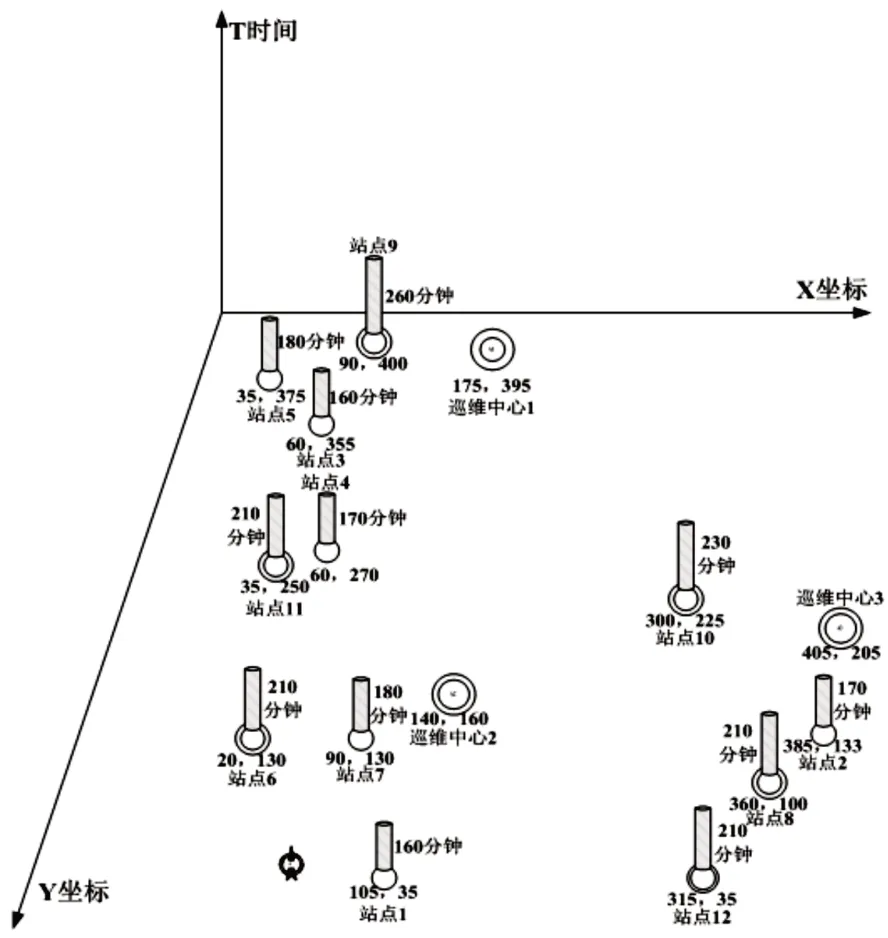
图2 群体互动时空分布图Fig.2 The Diagram of Group Interaction

通过机器人群体调度分配算法求解3 台机器人VRP 分别在12 个节点之间转移运用路径，通过远程集控后台输出满足距离最小等约束条件的调配方案，三台机器人的路径规划，如表2所示。

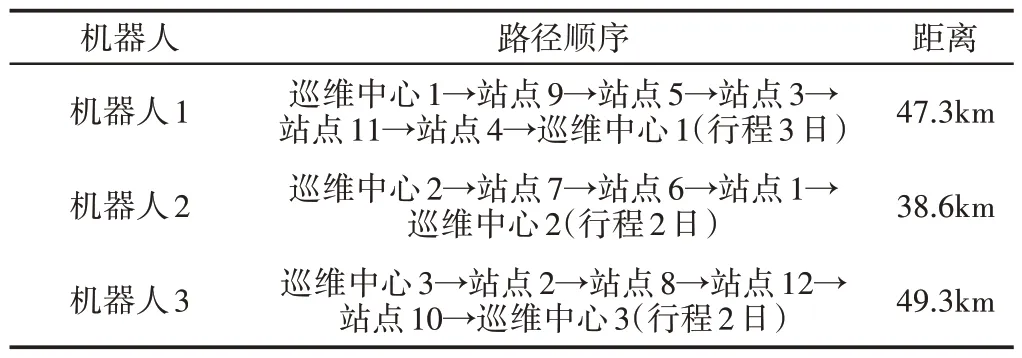
表2 路径规划方案Tab.2 The Scheme of Path Planning

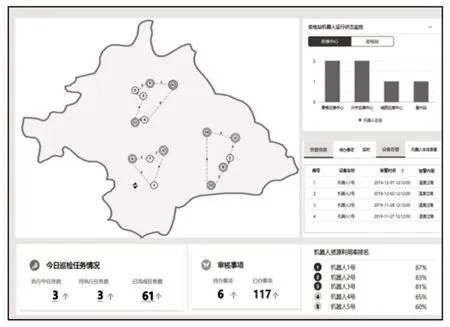
图3 输出的路径规划方案Fig.3 The Scheme of Path Planning

5 结论

基于时空特征的变电站机器人路径规划算法，针对机器人群体调度分配过程中的VRP问题，考虑时限和距离这两项约束条件，遍历式搜索最优路径，提出组合优化后的路径规划方案，实现充分应用机器人资源。其主要特点在于：

（1）在考虑多机器人、多起点的路径参数等拓扑网络布局情况下，针对多目标站点的路径规划逐步收敛至全局最优解，通过启发式遍历搜索可选路径的方式，避免陷入路径方案的局部最优。

（2）以变电站的横、纵坐标为第一维和第二维，以巡检所需时间为第三维，构建时空三维坐标系，用于分析满足时空约束条件，避免路径陷入复杂计算，有助于得到最优路径规划。