改进鲸鱼优化算法的机器人时间最优轨迹规划
刘 杰,卞新宇,王晓勇,栗 娟
(1.南京工业职业技术大学江苏省工业感知及智能制造装备工程研究中心,江苏 南京 210023;2.桂林电子科技大学海洋工程学院,广西 桂林 541004)
1 引言
有越来越多的工业机器人轨迹规划[1-4]应用实例表明,仅考虑连续性和平滑度的轨迹规划是不能满足大多数工业需求的。这就需要针对不同的任务要求对基础轨迹规划添加能耗、效率、冲击等约束条件,从而提升轨迹的性能。由于其计算过程复杂且繁琐,一般采用智能优化算法进行计算[5-6]。常用于轨迹规划研究的智能优化算法有遗传算法(Genetic Algorithm,GA)、粒子群优化算法(Particle Swarm Optimization,PSO)等[7-10]。常用的轨迹优化目标包含时间最优、能量最优、冲击最优等,一般选取以上一种或多种目标进行轨迹优化的研究。文献[11]将遗传算法与三次多项式插值相结合,以时间最优为目标,对多车型汽车生产流水线中的工业机器人做轨迹优化,实现了时间最短的优化目的,但此算法的优化结果受参数影响较大且全局搜索速度较慢。文献[12]以时间、加速度、跃度为优化目标,提出一种自适应罚函数的骨干粒子群优化算法,并结合NURBS曲线应用于机器人的零件加工,优化后各关节跃度与加工误差曲线表明优化后的加工时间、平稳性、加工精度均优于优化前的实验结果,此算法搜索能力虽快,但依旧受参数影响较大。文献[13]提出了一种改进的引力搜索算法,其借鉴人工蜂群算法的贪婪搜索策略,有效提高了收敛速度,并将其应用于六自由度重载机器人,结果表明该算法有效提高了解的质量和收敛性能,但计算过程较为复杂。
近两年,Seyedali Mirjalili和Andrew Lewis提出了一种新型元启发式算法—鲸鱼优化算法(Whale Optimization Algorithm,WOA)[14]。WOA 虽容易陷入局部最优解且收敛精度低,但相对于其他智能优化算法具有参数少、结构简单等优点。由于考虑到在智能制造生产单元中,6R 工业机器人负责上、下料的生产任务,降低生产节拍,提高上下料运送效率并减小冲击振动,这就需要将时间最优作为优化目标来提升机器人的作业效率。
为得到更准确的轨迹优化结果,针对WOA的缺点并结合工业机器人对轨迹规划的性能要求,这里提出一种非线性收敛因子并引入一种非线性惯性权重[15]以达到提高全局搜索能力、收敛精度和收敛速度的目的。将改进后的WOA(简称MWOA)与五次多项式相结合,基于实际应用场景对研究模型6R工业机器人做轨迹优化。
2 研究模型及轨迹规划
2.1 智能制造应用场景说明
2.1.1 研究模型概述
这里的研究模型为六自由度串联型工业机器人,如图1 所示。将其主要参数整理,如表1所示。
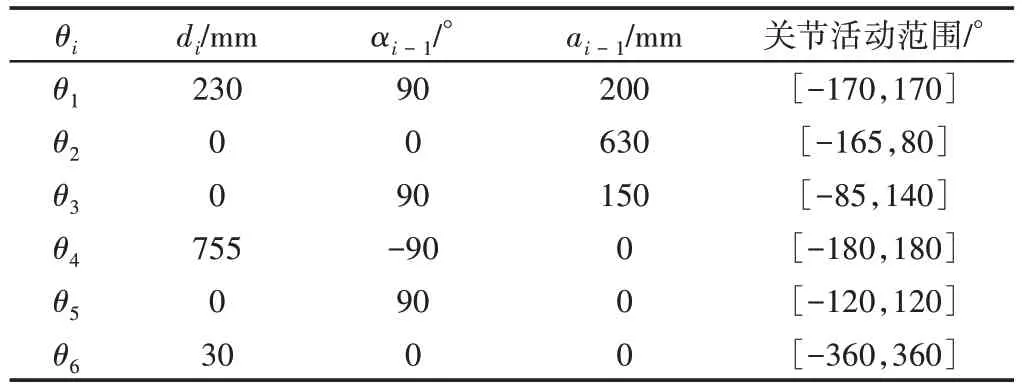
表1 研究模型主要参数Tab.1 The Main Parameters of the Research Model
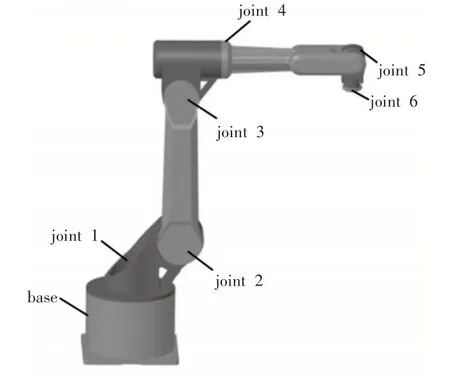
图1 研究模型Fig.1 Research Model
2.1.2 应用场景简述
该研究本体在智能制造生产线中,主要完成上、下料的任务,整个工艺流程大致为取生料、放置生料、生料加工、取出加工后的物料、将物料置于料仓,最终回归初始位置,主要涉及的主体包含6R工业机器人、加工中心和数字化立体料仓。通过Creo 4.0对以上三个单元建立简化的三维等效模型,并按照实际应用场景装配,如图2所示。
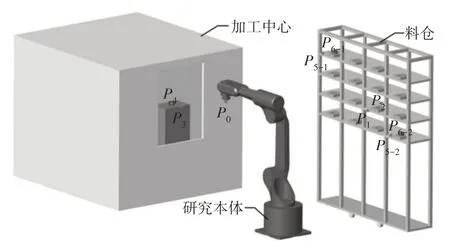
图2 应用场景及路径点分布Fig.2 Application Scenarios and Path Point Distribution
为避免仿真实验的偶然性,随机选取了两个物料点,并编号为A11和A44。同时,为了避免该研究本体在完成工作任务时发生不必要的机械碰撞,在需经过的路径点中添加了几个防撞点:P2、P3、P6-1以及P6-2。所有路径点均在图2 中用橙色点标出。由于将未加工的毛料放至加工中心进行加工需要一定的时间,故将整个工作任务分成两个阶段进行研究分析,且将其对应路径分别定义为路径一(依次经过P0、P1、P2、P1、P3、P4、P3、P0)和路径二(P0、P1、P2、P1、P3、P4、P3、P5-1/P5-2、P6-1/P6-2、P5-1/P5-2、P0)。
2.2 轨迹规划
为保证其整个运行过程的稳定性,各关节的位置、角速度、角加速度在整个运行时间内需保持连续性变化。
这就要求在进行插值计算时,插值函数需将各路径点平滑地连接。常用的轨迹插值计算方法有三次多项式插值[16]、五次多项式插值[17]和高阶多项式插值[18]。由于实际应用场景要求路径点需全部经过,且各关节角速度与角加速度均需约束,故采取五次多项式插值的方法对该模型进行轨迹规划。
其数学表达式为:
各路径点间的起止位置需满足以下约束条件:

3 鲸鱼优化算法
WOA是由Seyedali Mirjalili和Andrew Lewis[14]提出的一种新型元启发式算法,通过模拟座头鲸的螺旋式捕食模式寻找猎物。现将搜索空间近似为圆锥体(一色部分)、搜索路径近似为环绕于圆锥表面呈上升状的螺旋线(分别用一色实线与一色虚线表示两条随机搜索路线)、当前最优个体和目标位置近似为两个质点(一色部分),建立空间模型,如图3所示。
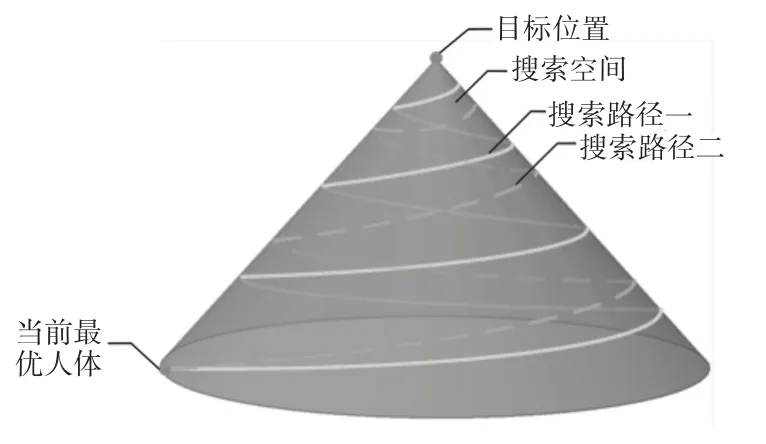
图3 螺旋式捕食模式Fig.3 Spiraling Patterns of Prey
座头鲸捕食猎物的过程分为包围猎物(即缩小搜索空间)、收缩包围(即螺旋更新位置)和猎物搜寻(即搜寻目标),针对上述三个捕食阶段分别建立数学模型。
3.1 缩小搜索空间
座头鲸种群在某一搜索空间中搜寻到猎物时,距离猎物最近的座头鲸(最优个体)会由当前位置通过随机路线逐渐地接近猎物,种群中其他的座头鲸会将最优个体作为接近目标间接接近猎物。建立数学模型时,种群中的最优个体对等于当前最优解。在WOA中假设座头鲸种群的数量为N,搜索空间是D维,描述此种捕食行为的数学形式为:

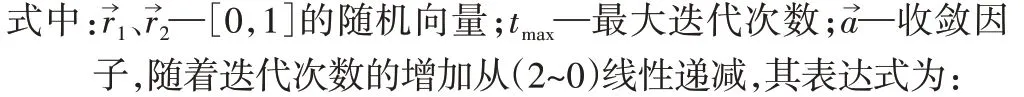
3.2 螺旋更新位置
座头鲸在捕食途中采取的是螺旋收缩包围的方式,即座头鲸的位置是呈螺旋更新的。将此行为应用到算法中,则螺旋捕食行为的数学模型建立如下:
由于座头鲸收缩包围猎物的行为和螺旋上升的行为是同时发生的,在位置更新时,需考虑到以哪一种迭代方式进行。此时将概率p作为判断阈值,根据不同的概率值选择对应的迭代方式,具体表达式如下:
式中:p—[0,1]的随机数;b—定义对数螺旋形状的常数;l—[-1,1]的随机数。
3.3 搜寻目标
以上两个阶段是以已知猎物位置为前提条件(即 |A|<1),若在尚未找到猎物相关信息的情况下(即 |A|≥1),座头鲸需通过不同的随机方式搜索猎物,该过程即为搜寻目标阶段,数学表达式对应如下:
4 改进的WOA
WOA虽具有参数少、结构简单、收敛速度快等优点,但是容易陷入局部最优解且收敛精度低[19]。针对上述缺点并结合工业机器人对轨迹规划的性能要求,提出一种非线性收敛因子并引入一种非线性惯性权重以达到提高全局搜索能力、收敛精度和收敛速度的目的。
4.1 引入惯性权重
为提高WOA的局部开发能力和收敛精度,通常在算法中引入惯性权重思想,但线性变化的惯性权重无法在实际迭代中得到良好的效果,故引入文献[9]中提出的一种非线性惯性权重ω,表达式如下:
式中:μ—常数系数,经多次实验取值0.01[9]。此时,惯性权重ω随着迭代数的增加非线性减少。
4.2 添加非线性收敛因子
在基本WOA的数学模型中,全局的探索能力主要受参数的影响,而影响的参数是收敛因子。若要提高WOA的全局搜索能力,就需要对收敛因子进行修改。由于基本的WOA中的参数是收敛因子。若要提高WOA的全局搜索能力,就需要对收敛因子为线性收敛,这就导致WOA在全局搜索中极易陷入局部最优,从而得到的计算结果不够准确。为保证实际寻优过程中迭代前期收敛速度快且后期收敛精度高,现提出一种非线性收敛因子,表达式如下:
当 |A|≥1时,位置更新公式应表示为:
4.3 MWOA算法步骤
算法基本步骤如下:
(1)将种群数量设置为N,随机产生初始种群的位置;初始化参数和最大迭代数为tmax。
(2)计算种群中每个鲸鱼个体(即搜索代理)的适应度值,选择适应度值最小的座头鲸个体,将其定义为当前最优个体,用X*表示其位置向量。
(4)将位置更新后的种群中的个体进行比较,确定出全局最优个体及当前位置。
(5)若迭代次数达到最大值,即达到了WOA中循环部分的终止条件,则输出结果;否则,需返回到步骤(2),继续计算,直至满足终止条件。
(6)输出结果,即全局最优解X*。
4.4 算法性能对比实验与分析
为验证MWOA 的有效性,基于标准测试函数进行仿真实验,如表2所示。其中,F1(x)、F2(x)、F3(x)为单峰测试函数,用来验证MWOA的收敛速度;F4(x)、F5(x)、F6(x)为多峰测试函数,用来验证收敛精度。
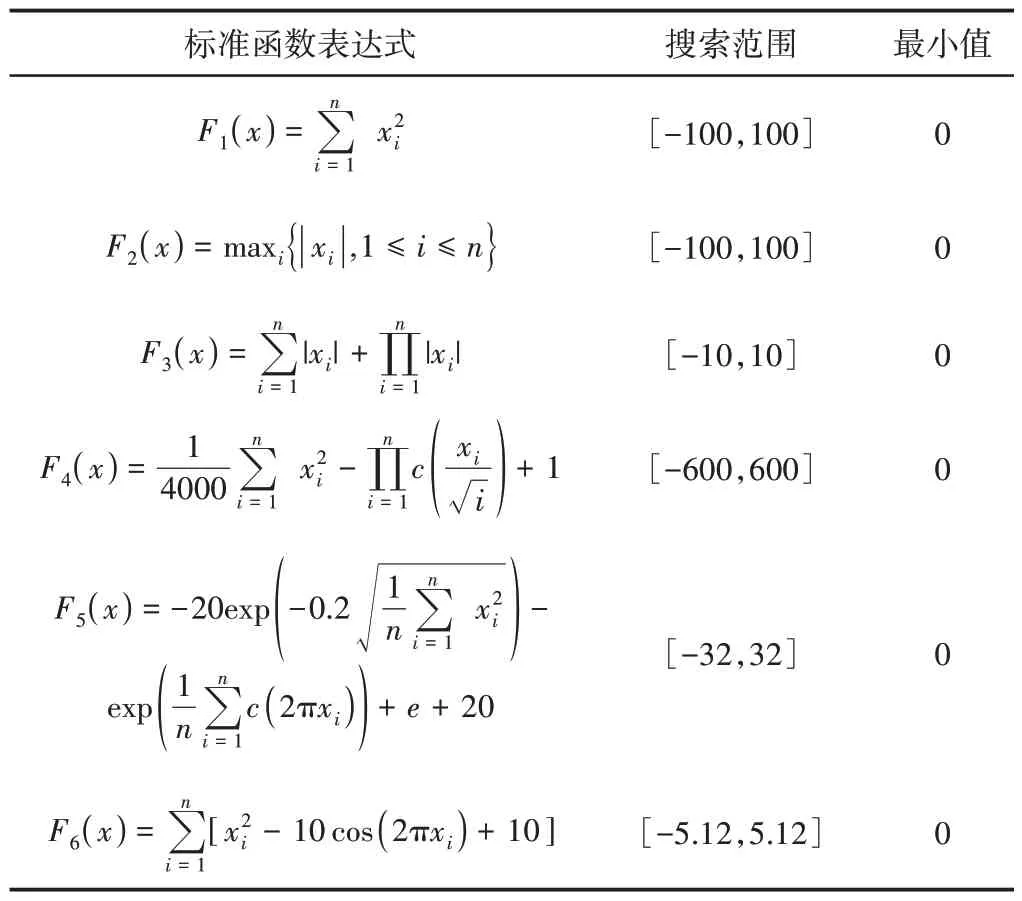
表2 标准测试函数Tab.2 Standard Test Function
在进行仿真实验时,添加基本WOA、PSO、GA 和MWOA 四种算法进行对比分析。将初始化种群的数量N设定为30,最大迭代数tmax为800,基于标准测试函数对选取的各算法分别进行40次运算,取多次运算结果的平均值和方差进行对比结果,如表3所示。
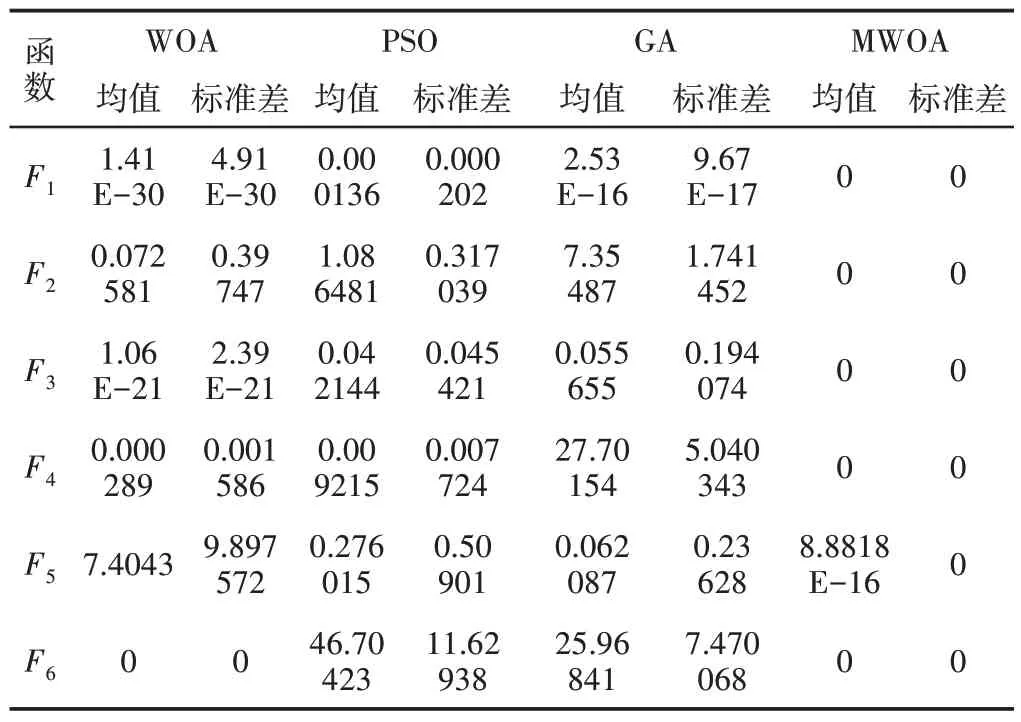
表3 测试函数的计算结果Tab.3 The Result of the Test Function
将表3中各算法的均值和标准差进行比较可知:测试函数F1至F6的计算结果中,MWOA的均值和标准差均为最优值,说明该算法的收敛精度、收敛速度和算法稳定性均优于算法WOA、PSO和GA。因此,MWOA 可用于后续轨迹优化的研究中。现基于MATLAB R2018b平台对算法WOA、PSO、GA以及MWOA进行仿真实验,实验结果,如图4所示。
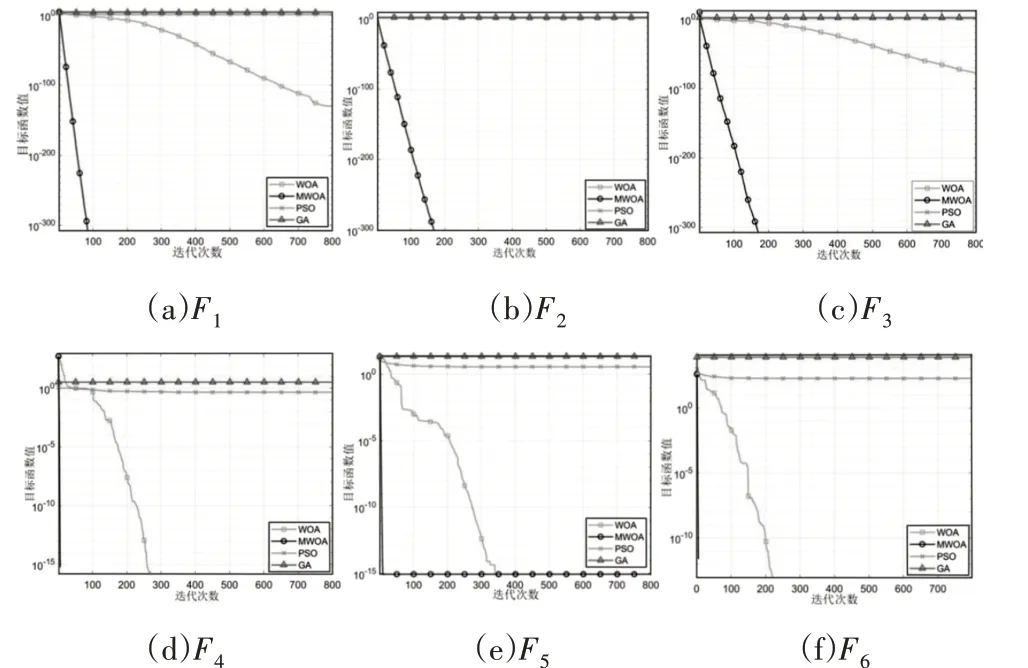
图4 测试函数的迭代收敛曲线图Fig.4 Iterative Convergence Graph of the Test Function
由图4可知:
(1)由图4(a)~图4(c)中各算法的收敛曲线可知:随着迭代次数的增加,GA 与PSO 对应的函数值近似为1,WOA 对应的函数值小于上述两种算法的函数值,而MWOA对应的目标值最小且无限接近于0,说明较于WOA、PSO和GA,MWOA具有更快的收敛速度;
(2)图4(d)~图4(f)结果显示:GA对应的三组函数值均大于1,PSO对应的函数值略小于GA,WOA对应的函数值虽比GA与PSO小,但仍大于MWOA,MWOA对应的函数值在迭代次数未达到20次之前均已收敛至全局最小值,说明MWOA较于其他三种算法具有更高的收敛精度。
5 时间最优轨迹规划
5.1 轨迹优化模型
由于该6R机器人完成一次上、下料任务消耗的时间主要与各关节的角速度和角加速度有关,若以时间为优化目标,需添加角速度、角加速度、角加加速度等运动学参数的最大值作为约束条件,则约束条件可表示为:

式中:T—整个加工过程的总时间;T1T1—路径一的运动时间;T2T2—路径二的运动时间。
现将轨迹优化模型的约束条件和各路径点对应的关节角度值分别整理,如表4、表5所示。
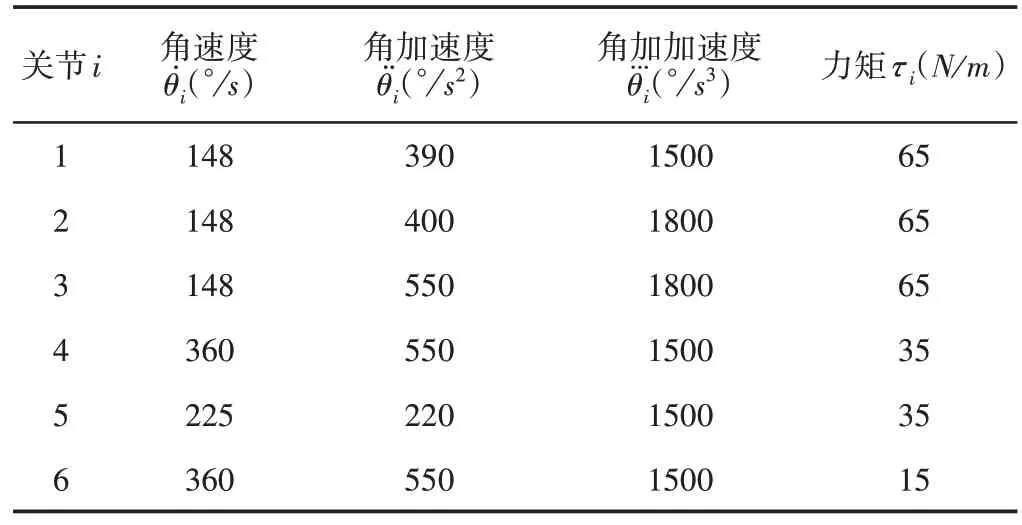
表4 关节约束条件Tab.4 Constraints on the Joint
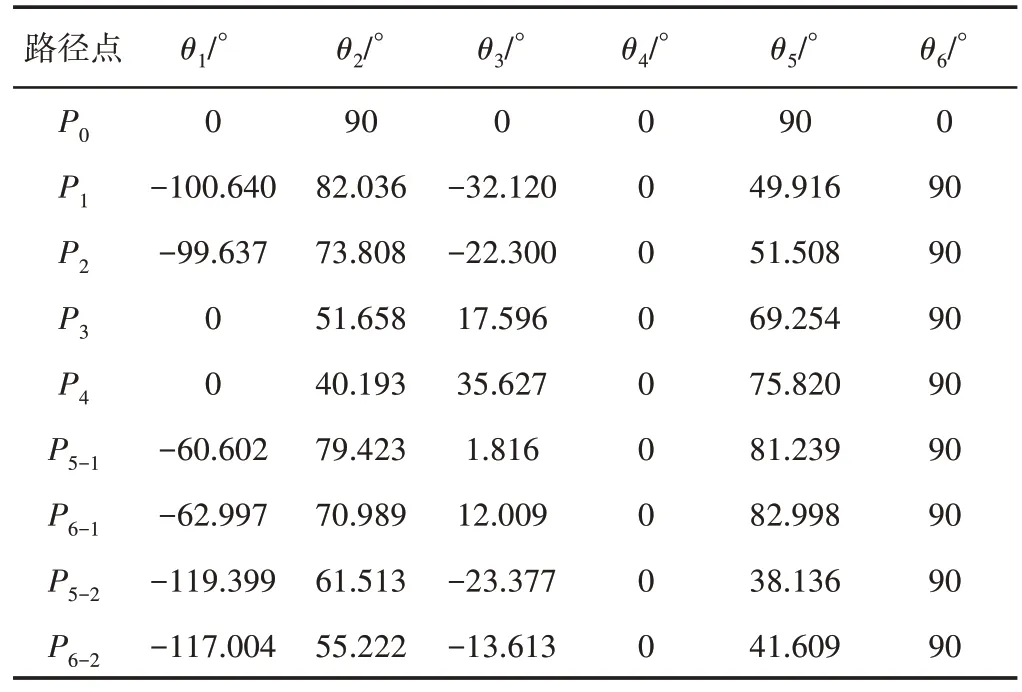
表5 关节角度值Tab.5 The Angle of the Joint
5.2 轨迹优化
现基于MWOA和五次多项式插值对研究本体做时间最优轨迹优化。该仿真实验的初始化种群数量N设定为30,最大迭代数tmax定义为500,优化前各路径的运行时间均设定为t=[0,2,3,4,6,7,8,10]。
为保证仿真实验结果的科学性,经过多次仿真优化,得到6R机器人两段路径的运行总时间,如图5所示。同时将每个路径点之间的时间优化结果整理,如表6所示。由于研究本体的第四个关节角度值在整个运行过程中并未发生变化,因此不对其时间间隔作相关整理。

表6 关节角度值Tab.6 The Angle of the Joint
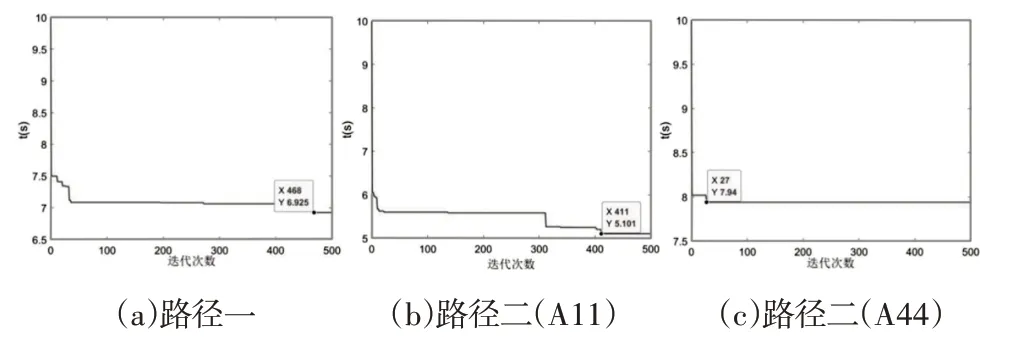
图5 时间优化的仿真结果Fig.5 Simulation Results of Time Optimization
由图5 可知:(1)图5(a)显示:当MWOA 迭代到约第470 次时,路径一对应的时间函数目标值几乎收敛至最小值,即minT1=6.925s,相对于计划时间缩短了3.075s;(2)由图5(b)可知,当MWOA迭代到约第411次时,路径二中到达取料点A11对应的时间函数的目标值收敛至最小值,即minT2_A11=5.101s,相对于计划完成时间缩短了4.899s;(3)从图5(c)可得到,当MWOA迭代到第27次时,路径二中到达取料点A44对应的时间函数的目标值收敛至最小值,即minT2_A44=7.94 s,相对于计划完成时间缩短了2.06s。
基于上述理论基础,经MATLAB仿真,得到各路径轨迹优化的运动参数曲线图,与优化前的轨迹规划结果进行对比,由于篇幅有限,只对路径一和到达放料点A11的路径二做轨迹规划,如图6、图7所示。由图6、图7的仿真结果可知:(1)优化前:路径一与路径二(A11)对应的各关节角度、角速度与角加速度曲线图均连续且光滑,整个过程无突变现象,说明轨迹优化前的工业机器人运动过程稳定性较好,且均按照规定的10s运动时间完成轨迹规划;(2)优化后:基于MWOA在原轨迹规划的基础上进行时间优化后,路径一与路径二(A11)的运行时间分别缩短了3.075s和4.899s,且得到的各关节角度、角速度与角加速度曲线图仍连续光滑无突变,说明该轨迹优化结果实现了时间最优的优化目标,且保证了原有的稳定性。
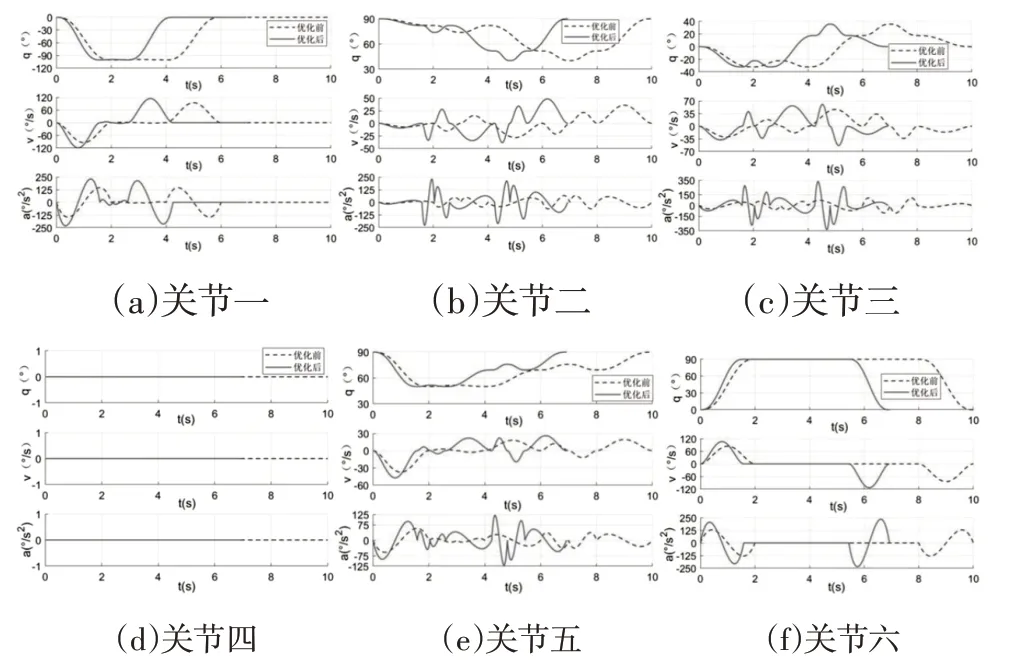
图6 路径一的时间优化仿真结果Fig.6 Time Optimization Simulation Results of Path 1
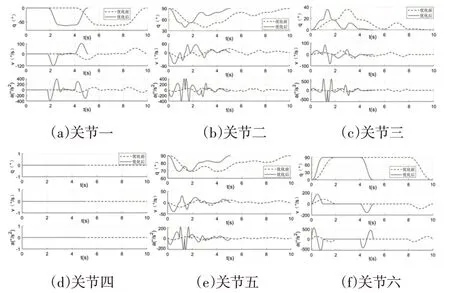
图7 路径二(A11)的时间优化仿真结果Fig.7 Time Optimization Simulation Results of Path 2(A11)
6 结论
(1)提出一种非线性变化的收敛因子,并引入非线性惯性权重对基本WOA进行改进后得到MWOA。将此算法与基本WOA、PSO和GA的均值与标准差进行对比分析,结果证明MWOA具有更高的收敛速度、收敛精度以及全局搜索能力。(2)将其应用于智能制造单元中的6R工业机器人的轨迹优化中,实验结果表明,基于MWOA的轨迹优化在保证研究本体运行平稳的同时,各路径的运行时间分别缩短了约30%、49%和20%,达到了时间优化的目的,可为相关领域的研究提供一定的参考价值和理论支撑。

