一种位置和图像相切换的视觉伺服仿真分析
徐冰辉,张 磊,姚兴田,苏波泳
(南通大学机械工程学院,江苏 南通 226019)
1 引言
智能化的时代,对机器人的需求也朝着智能化,多功能化的方向转变,将视觉伺服技术加入机器人系统中能有效的提高机器人的自动化程度,对扩大机器人的应用领域有着重要意义。
目前,机器人视觉伺服技术已广泛运用于产品分装、货物搬运与装配、机器人焊接[1]、喷漆[2]等领域。但实际应用中仍然有许多关键问题需要解决,比如特征信息采集的稳定性、机械手的位姿估计精度、机器人视觉伺服的局限性等。事实上,这些关键问题将直接影响机器人的伺服效果,因此,研究机器人视觉伺服技术对提高机器人抓取效果显得十分重要。
视觉伺服的概念由文献[3]在1979 年提出,首次将闭环系统引入视觉控制中,与传统视觉反馈方式不同的是将图像处理与反馈同时进行,提高了控制精度。1980 年,Weiss 将视觉伺服区分为基于位置和基于图像两大类,之后出现的视觉伺服大多基于这两大类。文献[4]通过当前图像与目标图像之间的对极几何关系获取两幅图像间的位置方向参数。文献[5]在此基础上结合了神经网络控制,驱动欠约束机器人运动到期望位置并完成抓取。而文献[6]通过分解当前图像与目标图像之间的本质矩阵计算得到旋转和平移信息,同样完成了伺服任务。文献[7]增加了相机视野以及机械臂关节的限制的约束,研究出了基于势场法的视觉伺服方法,有效的避免了图像局部最小化的问题。文献[8]将位置视觉伺服与PD 控制器结合,实现了对目标的运动跟踪。文献[9]将CAD模型映射到图像空间,使其收敛至目标边缘,实现了对物体的三维跟踪。文献[10]采用随机搜索树(RRT),提取出从初始位姿到目标位姿的路径,最终利用图像伺服进行跟踪。
经过多年的发展,大多数对视觉伺服的研究基本是基于位置视觉伺服或基于图像视觉伺服的延伸,一些视觉伺服的本质问题很难解决。如在位置视觉伺服中,伺服精度囿于机器人的运动学模型误差;又比如在图像视觉伺服中,只有当机械手在接近期望位姿的区域内才能保证伺服的稳定性[11]。这里以特征点作为输入信号,在Eye-to-Hand系统的基础上结合基于图像视觉伺服有着较好的鲁棒性、局部稳定性和收敛性[12]的优点,以及基于位置的视觉伺服控制算法简单、系统响应快的优点,设计了一种切换控制器将两者优势相结合,提高机器人综合视觉伺服效果。采用六自由度机器人,在伺服的前期选用位置伺服,使机械手能迅速到达目标物的邻域内,然后在伺服的后期选用图像伺服,不断纠正机械手与期望位姿的偏差,使其最终到达指定期望位置。
2 机器人视觉伺服控制研究
2.1 位置视觉伺服原理
基于位置的视觉伺服中,图像特征为目标物的三维位姿。坐标系模型,如图1所示。在该视觉伺服中{W}表示机器人坐标系同时也是世界坐标系;{E0}表示机械手即机器人末端执行器的初始坐标系;{E}表示末端执行器的当前坐标系;{E*}表示末端执行器需要到达的期望坐标系;{C}表示摄像机坐标系。
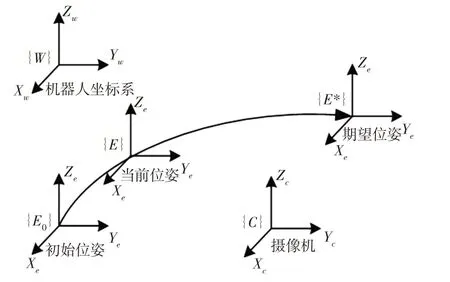
图1 坐标系模型Fig.1 Coordinate System Model
基于位置视觉伺服的主要目的是输出关节量Δθ=[q1q2q3q4q5q6]T控制六自由度机器人使末端执行器从初始位姿{E0}运动至期望位姿{E*}。采集到的特征点P通过PnP方法[13]可以计算出末端执行器相对于摄像机的实时位姿,而末端执行器期望位姿事先已给定为Tce*,根据位姿体系可以得出末端执行器当前位姿与期望位姿的偏差e为:
在末端执行器从初始位姿移动到期望位姿时,由于是Eyeto-Hand系统,即摄像机相对于机器人坐标系的位姿Twc是固定的,并且可以通过手眼标定获得,最终可以较容易地得到末端执行器相对于机器人坐标系的位姿Twe为:
将位姿矩阵Twe0与Twe*代入由D-H法建立的机器人逆运动学模型可分别求解出机器人初始关节变量θ0和期望关节变量θ*,则该六自由度机器人需要输出的关节量Δθ为:
在实际情况中,位姿的变换可能是相当大的,上述运动往往不能一步到位,因此需要在每个采集周期更新一次位姿,最终不断靠近期望位姿。由于上式(3)中用到的D-H 法建立在机器人各关节的机械尺寸上,涉及到的关节轴线交点、公垂线等参数都是难以确定的空间几何数据。虽然通过视觉反馈可以弥补D-H建模带来的定位误差,但是在精度上仍然不尽如人意。并且零件的加工误差、齿轮的啮合间隙等都会产生系统误差,因此最终的伺服结果很难等收敛。
2.2 图像视觉伺服原理
基于图像视觉伺服的图像特征定义在图像平面上,在伺服过程中摄像机实时采集机械手图像,得到机械手的特征和期望特征的偏差作为偏差信号,通过图像视觉伺服方法完成伺服任务。
这里定义的图像偏差信号为:
式中:p*—期望的像素坐标;p—当前像素坐标。
由像素平面特征点的速度可以计算出特征点在世界坐标系下的速度υ。这里采用一个简单的线性控制器:
式中:λ—增益系数。
得到在世界坐标系下特征点的速度为:
式中:Jp—特征点的图像雅克比矩阵。
由于图像伺服最终驱动的是机器人的关节,特征点在世界坐标系下的速度最终还需转为机器人的关节速度,而机器人雅克比矩阵就建立了关节速度与机器人末端手抓在世界坐标系下的速度之间的数字关系。最终我们可以得到机器人的关节速度为:
式中:Jq-1—机器人雅克比矩阵的伪逆矩阵。
在采样周期Tε的离散系统下可以得到机器人k时刻下关节变化量为:
由于基于图像的视觉伺服方法不涉及机械手机械尺寸的建模,因此系统误差较小,随着机械手的位置不断被伺服调整,最终伺服结果能达到收敛。
2.3 视觉伺服系统设计
这里将一个决策控制器和两个视觉伺服控制器组合,形成简单的切换系统。其中一个视觉控制器是基于位置视觉伺服,另一个是基于图像视觉伺服,切换系统结构,如图2所示。
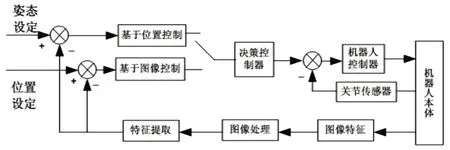
图2 控制系统结构图Fig.2 Control System Structure
按照这里提出的视觉伺服控制方法,可以将该伺服过程分为两个阶段,(1)机械手离期望抓取位置较远时为第一阶段,采用位置视觉伺服方法;(2)机械手靠近期望抓取位置时为第二阶段,采用图像视觉伺服方法。
切换示意图,如图3所示。图中:{E}—当前机械手坐标系;{E*}—机械手最终到达的期望位姿坐标系;d—机械手坐标系原点与期望位姿坐标系原点在世界坐标系下的距离;ε—期望位姿的邻域半径。选用d作为切换信号,当d大于给定的域值ε时选用基于位置的视觉控制器,当d小于给定的域值时选用基于图像的视觉控制器。切换控制伪代码如下:
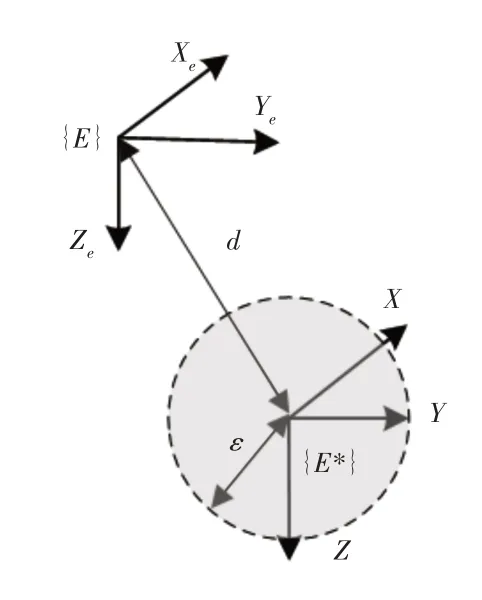
图3 切换示意图Fig.3 Switching Diagram
本研究使用Matlab/Simulink软件,根据上述切换规则建立的机器人视觉伺服结构图,如图4所示。
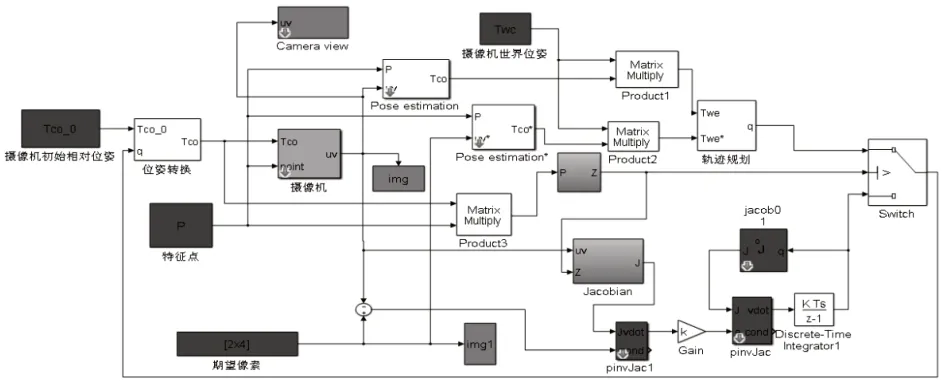
图4 切换伺服系统结构图Fig.4 Switching Servo System Structure
2.4 探机器人视觉伺服模型建立
这里使用Matlab 软件中的Robotics Toolbox 工具箱进行建模,以puma560机器人为实例对象,以目标物体上构造的4个角点为特征点,在机械手末端执行器坐标系中的坐标(单位:m)分别为(0.12,0.2,0)、(-0.12,0.2,0)、(0.12,-0.2,0)、(-0.12,-0.2,0)。摄像机焦距为10mm,帧率为25帧/秒,分辨率为512×512,像素的物理尺寸dx=dy=0.01mm,图像平面的主点坐标为(256,256),经成像变换后特征点的初始像素坐标为:(357,218)、(257,364)、(166,290)、(255,160),期望的像素坐标为:(423,89)、(423,423)、(89,423)、(89,89)。为了模拟一个更加真实的环境,在机械手和摄像机的参数上添加了10%的建模误差,所建立的机器人视觉伺服模型,如图5所示。其中,世界坐标系、摄像机坐标系、物体坐标系、机械手末端坐标系分别为{W}、{C}、{O}、{E},已知机械手末端的初始位姿Twe,摄像机相对于世界坐标系下的位姿Twc,摄像机、机械手以及目标特征点的初始位置如图所示,其中‘*’表示目标特征点。为了完成视觉伺服任务,机械手将带动目标特征点一起运动至期望位置。
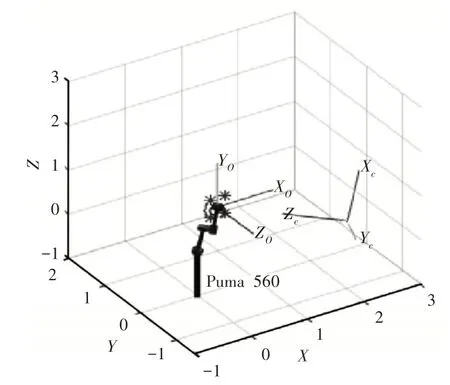
图5 机器人视觉伺服仿真模型Fig.5 Robot Visual Servo Simulation Model
2.5 视觉伺服系统的仿真分析
在初始条件相同的情况下分别采用基于位置、基于图像、和这里使用的视觉伺服方法对其仿真,其中对切换控制器仿真时,设置阈值ε为0.15。仿真结果,如图6所示。图中描述了机械手在移动过程中,摄像机采集的特征点在图像平面的运动轨迹,以及当前像素坐标与期望像素坐标的误差随时间的变化。其中‘×’表示特征点的初始位置,‘o’表示特征点的期望位置,‘•’表示特征点移动路径。
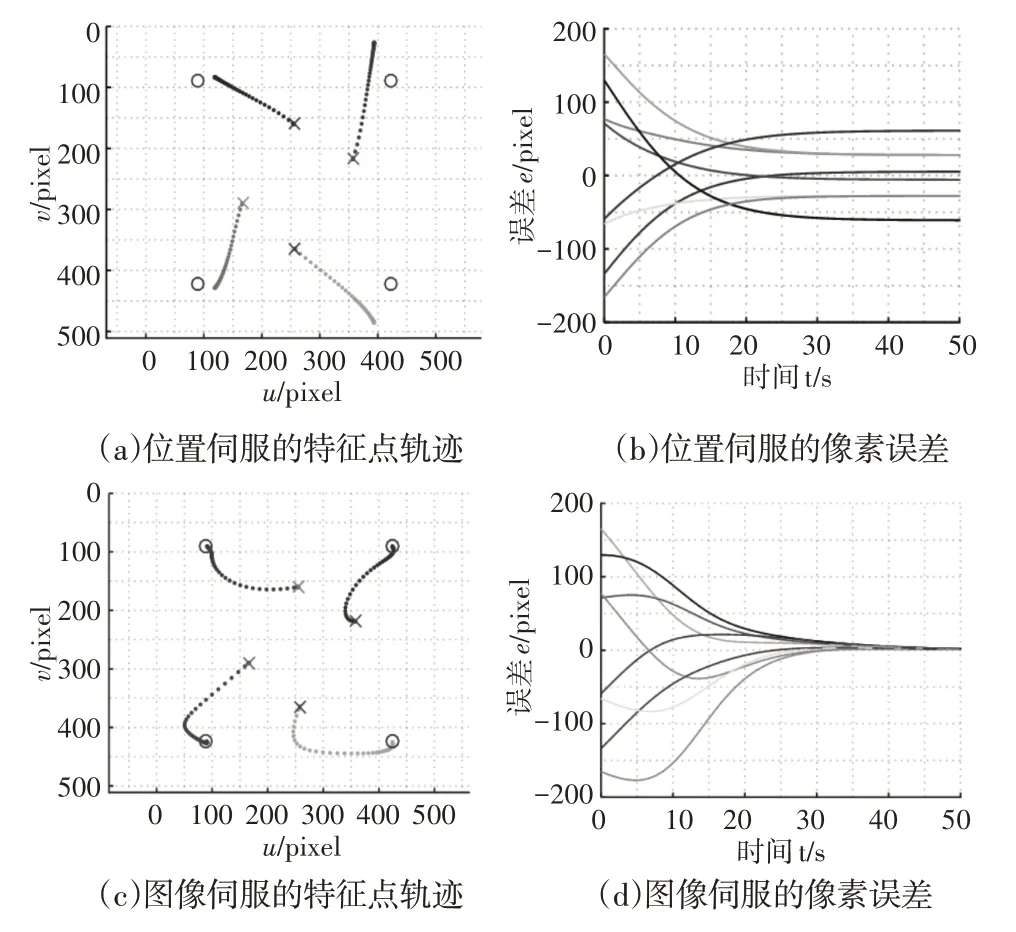
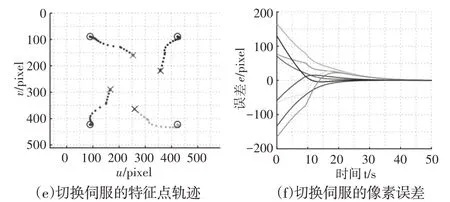
图6 三种视觉控制算法仿真结果Fig.6 Simulation Results of Three Visual Control Algorithms
由图6(a)可知,特征点可以逐渐靠近期望位置,20s后伺服接近停止,但是不能达到期望位置,并且从图6(b)可以发现图像像素点的误差最终并不能收敛于零,这与上述分析的位置视觉伺服方法最终的伺服结果很难收敛的结果相一致。由图6(c)可知,基于图像的视觉伺服可以使特征点移至期望位置。图6(d)表明特征点的像素误差随着伺服时间的增加逐步收敛于零,运行45s后伺服接近停止,说明该控制器对机械手运动学模型误差和摄像机模型误差并不敏感,能较高精度地完成视觉伺服任务,但相比位置伺服运行时间较长。结合基于位置和图像伺服的切换伺服策略后,由图6(e)可看出前半程伺服运动与图6(a)是相同的,这是因为在系统没有达到切换条件前选用的是基于位置视觉伺服,并且与位置视觉伺服相比可以发现特征点最终能够达到期望位置,完成伺服任务。由于在前半程选用的是位置视觉伺服,而且通过上述分析可以知道位置视觉伺服的伺服时间短,因此使用该方法与基于图像相比可以缩短一定的时间,从图6(f)可以发现,整个视觉伺服过程在35s 左右图像特征误差收敛于0。通过计算可得,在基于位置视觉伺服中,机械手最终伺服停止的位置与期望位置的距离值d1=0.1081m;在基于图像视觉伺服中,机械手最终伺服停止的位置与期望位置的距离值d2=0.002m。采用切换视觉伺服时,阈值ε选取不同值时,距离值d也不同,如图7所示。
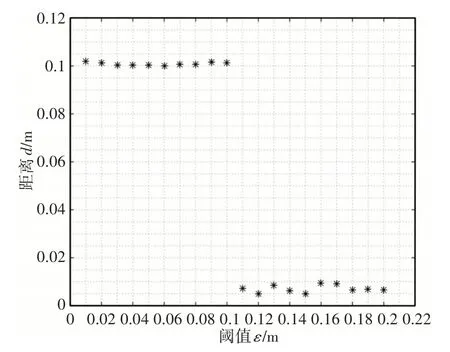
图7 视觉伺服中不同阈值ε对应的距离值dFig.7 Distance Value d Corresponding to Different Threshold ε in Visual Servo
由图7可知,当阈值ε<0.1时,机械手最终伺服停止的位置与期望位置的距离值d在0.1m左右,这是因为切换系统首先运行的是位置视觉伺服,并且自始至终切换信号d>ε,无法满足切换条件,最终如位置伺服一样特征点无法达到期望位置,伺服失败。
当阈值ε>0.1时,切换信号d将在位置视觉伺服中一直减小到ε,此时触发切换条件,然后在图像视觉伺服中距离值d将一直减小,特征点到达期望位置,伺服成功。当阈值ε分别取0.11以及0.09,其余条件与上述仿真初始条件相同,分别代入切换伺服控制器,当前像素坐标与期望像素坐标的误差随时间的变化,如图8所示。从图8(a)可以发现系统达到切换条件,伺服成功;从图8(b)可以发现当阈值ε<0.1时,像素误差变化如上图8(b)一样,说明系统一直采用基于位置的视觉伺服,没有触发切换条件,以上两种仿真结果与本节对阈值ε范围的分析完全相同。事实上,d1的值本质上反映的是位置视觉伺服中机械手运动学模型误差和摄像机模型误差,而采用切换视觉伺服目的就是当机械手即将到达位置视觉伺服最终的平衡位置时及时切换成图像视觉伺服,从而减少机械手运动学模型误差和摄像机模型误差对视觉伺服的影响,使机械手快速准确的到达指定位置。
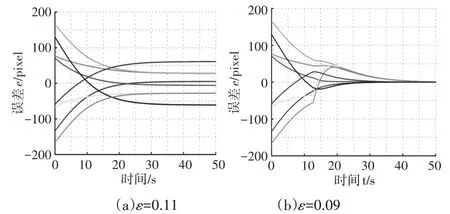
图8 基于切换伺服不同阈值下的特征像素误差Fig.8 Characteristic Pixel Errors Based on Different Threshold of Switching Servo
3 结论
这里结合基于图像伺服和基于位置伺服的优点在机器人伺服系统中设计一种切换控制器。在伺服的前期选用位置伺服,使机械手能迅速到达目标物的邻域内;在伺服的后期选用图像伺服,不断纠正机械手与期望位姿的偏差,使其最终到达指定期望位置,完成伺服任务。通过上述仿真实验可以发现,该切换视觉伺服充分的发挥了两个子控制器的优点,在前半程可以快速达到物体附近,后半程利用图像伺服可以使机械手精确到达期望位置,最终较快、较准地完成伺服任务。并且为了快速完成伺服任务,应使机械手在位置视觉伺服中距离期望位置越近越好,然而在切换系统中设定的阈值并不是越小越好,还要考虑到位置伺服子控制器中机械手最终与期望位置的距离,否则达不到切换条件。

