导数隐零点问题中虚设零点的方法

李发明

(山东省泰安第一中学 271000)

导数在高考解答题中始终扮演着压轴题的角色，主要考查的题型有导数与不等式的证明、恒成立与能成立问题、零点问题、洛必达法则、隐零点问题以及极值点偏移问题.本文将对隐零点问题中较难的虚设零点法的几个类型进行归纳总结，以期对学子及同行有所帮助.

1 可以消掉隐零点得到具体值的问题

例1 已知函数f(x)=xex-x-lnx，求f(x)的最小值.

解析定义域为x∈(0，+∞)，

所以f′(x) 在(0，+∞)上单调递增.

又因为f′(1)=2(e-1)>0，

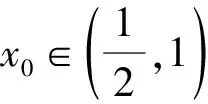
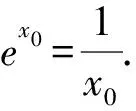
①

即x0=-lnx0.

②

所以f′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以f(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.

所以f(x)min=f(x0)=x0ex0-x0-lnx0.

将①②两式代入,得

练习1 已知函数f(x)=xe2x-2x-lnx，求f(x)的最小值.

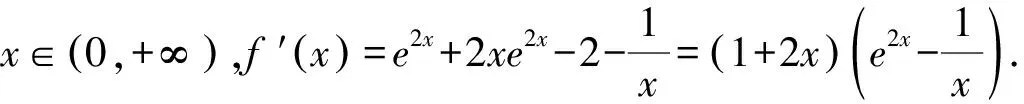
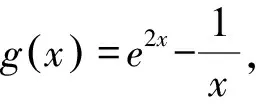
③

两边取自然对数得2x0=-lnx0.

④

所以g(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以f′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以f(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.所以f(x)min=f(x0)=x0e2x0-2x0-lnx0.

将③④两式代入,得

2 无法消掉隐零点的求范围问题

例2 已知函数f(x)=x+2xlnx，若对于任意x>1，f(x)>k(x-1)恒成立，求整数k的最大值.

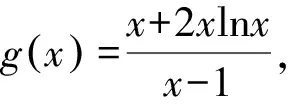
即2x0-2lnx0-3=0.

此时g′(x)在(1，x0)上为负，在(x0，+∞)上为正.

所以g(x)在(1，x0)上单调递减，在(x0，+∞)上单调递增.

所以kmax=4.

练习2 设函数f(x)=ex-x-2，当x>0时，(x-k)f′(x)+x+1>0恒成立，求整数k的最大值.

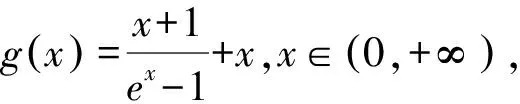
令h(x)=ex-x-2，易知h(x)在(0，+∞)上单调递增.

又因为h(1)=e-3<0，h(2)=e2-4>0，

所以存在x0∈(1，2)使得h(x0)=0，即ex0=x0+2.

所以h(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.

所以kmax=2.

3 无法消掉隐零点且需要放缩的求范围问题

例3已知函数f(x)=ex-ln(x+m)，当m≤2时，证明:f(x)>0.

解析当m≤2时，ln(x+2)≥ln(x+m)，所以-ln(x+2)≤-ln(x+m).

所以只需证明当m=2时，f(x)=ex-ln(x+2)>0,x∈(-2,+∞)即可.

⑦

两边取自然对数,得x0=-ln(x0+2).

⑧

所以f′(x)在(-2，x0)上为负，在(x0，+∞)上为正.所以f(x)在(-2，x0)上单调递减，在(x0，+∞)上单调递增.

所以f(x)min=f(x0)=ex0-ln(x0+2).

将⑦⑧两式代入,得

所以当m≤2时，f(x)>0.

点评对于含有参数m的不等式问题，通过分析当m≤2时函数f(x)的变化情况，找到f(x)取最小值的情况，将证明ex-ln(x+m)>0放缩为证明ex-ln(x+2)>0.此放缩有两个好处，一是将变化的参数m固定成了定值2；二是方便求导、方便计算.

练习3 已知函数f(x)=ex-t-lnx，当t≤2时，证明：f(x)>0.

解析当t≤2时，ex-t≥ex-2，所以只需证明当t=2时f(x)>0即可.

当t=2时，f(x)=ex-2-lnx，x∈(0，+∞)，

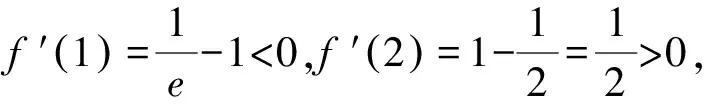
⑨

两边取自然对数得x0-2=-lnx0.

⑩

所以f′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以f(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.所以f(x)min=f(x0)=ex0-2-lnx0.

将⑨⑩两式代入,得

所以当t≤2时，f(x)>0.

4 需要对隐零点满足的方程进行二次化简的问题

例4设函数f(x)=xex-lnx-kx+x-1，若f(x)≥0恒成立，求实数k的取值范围.

(*)

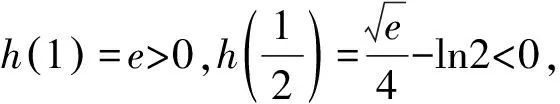
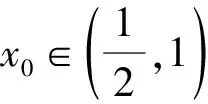
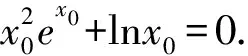
令F(x)=xlnx，所以F′(x)=lnx+1.

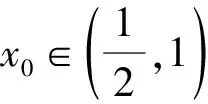
易知f′(x)>0在x∈(1，e)上恒成立.

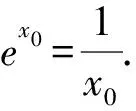
即x0=-lnx0.

所以h(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.

所以k≤2.

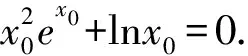
练习4设函数f(x)=xe2x-lnx-kx，若f(x)≥1恒成立，求实数k的取值范围.

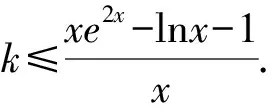
令h(x)=2x2e2x+lnx，x∈(0，+∞)，

所以h(x)在(0，+∞)上单调递增.

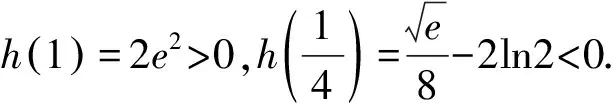
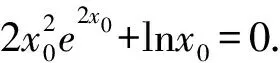
两边取自然对数,得

令F(x)=x+lnx，易知F(x)在(0，+∞)上单调递增.

即2x0=-lnx0.

所以h(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g′(x)在(0，x0)上为负，在(x0，+∞)上为正.

所以g(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增.

所以k≤2.

隐零点问题是高考导数压轴题最常考的类型之一，虚设零点法则是其中难度较大、出现较频繁的题型，它能综合考查学生对导数掌握的熟练程度，学生应在理解透“虚设零点”的基础上多加练习，以期熟能生巧.