函数零点问题中参数范围的解法探究
贺凤梅
(新疆伊犁巩留县高级中学 835400)
1 问题呈现
题目(新疆维吾尔自治区2022年普通高考第二次适应性检测理科卷第10题)若函数f(x)=x3-ax2+ex-lnx有两个零点,则a的取值范围为( ).


2 总体分析
本题题设简洁,将函数、导数、零点等知识有机结合起来,多层次、多角度地考查了学生的数学思维和核心素养,同时考查了学生利用导数解决问题的能力,对逻辑推理、数学运算等提出了较高的要求.本题解法多样,可以直接利用参变分离法求解;也可以利用分离函数法解答,利用导数的几何意义,即切线的斜率求解入手,再从相切逆推至函数图象相交的情况,进而求出参数的取值范围;可以根据零点个数,分类讨论细化解题,求出a的范围;作为选择题,还可以借助题设和选项的特点,利用排除法得出正确答案.但每种方法操作均不容易,在解题过程中会碰到一些障碍.下面具体分享一下,希望能帮助学生找到解决这类问题的突破口.
3 试题解答
视角1 分离参数,构造函数.
解法1 因为x>0,所以函数f(x)=x3-ax2+ex-lnx有两个零点等价于f(x)=0有两个正根.
分离参数,得

令h(x)=x3-ex+2lnx-1,则





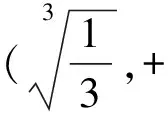


从而h(x)在(0,+∞)上单调递增,

①
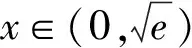




又当x→0时,
由洛必达法则知g(x)→+∞;
②
当x→+∞时,
则g(x)→+∞.
②

故选B.

下列关于函数f(x)=(2x-x2)ex的判断正确的是( ).
(1)f(x)>0的解集是{x|0 (3)f(x)没有最小值,也没有最大值. 为了降低①的风险,我们有新的处理方式如下: 解法2 结合解法1, 下同解法1. 评注此种处理方法需要较高的观察能力和配凑思维,值得我们思考和借鉴,提高解题能力.导数中有的零点是较难处理的,需要很多代数技巧作支撑,也要充分利用零点解题,尤其是隐零点,它可以帮助我们化超越函数为基本初等函数,还可能起到降次的作用,整体代换后还可能达到消元的目的. 视角2 分裂原函数,构造新函数. 解法3 令f(x)=x3-ax2+ex-lnx=0(x>0), “信息中心就‘选择哪些考评维度,数据如何分类’等核心问题广泛征询各部门意见,形成建设思路;几经例会讨论确定管理平台初步框架,多次深入各职能科室及临床一线征询意见,达成一致并上线运行。” 中心副主任赵前前回顾了平台“由思到行”、逐步完善的建设历程。试运行阶段,平台界面又经历了4~5次较大改版,最终形成了各方普遍认同的,覆盖全院、科室、医生的三级绩效评价体系。 令φ(x)=2x3-1+lnx, 所以φ(x)=2x3-1+lnx在(0,+∞)上单调递增, 当x∈(0,x0)时,g′(x)<0, 当x∈(x0,+∞)时,g′(x)>0, 所以g(x)在(x0,+∞)上单调递增. 整理,得切线斜率 整理,得t3+2lnt-et-1=0. ③ 代入直线y=ax-e中,得 故选B. 解法4 由x3-ax2+ex-lnx=0(x>0),得 同理可解. 评注解法4和解法3有异曲同工之妙,本质是两个函数图象整体平移,不再赘述,感兴趣的同仁可以自行试验一下.事实上,构造函数没有特殊的要求,关键在于新函数易于研究,直观形象就好.这一点对学生来说是一个挑战,形异质同解法会带来解题创新思路,对学生的能力提升大有裨益. 当然我们也可以直接转化为函数f(x)=x3-ax2+ex-lnx的图象与x轴交点的个数,分类讨论求出参数a的范围,此法求解原则上可行,但运算量较大.讨论中要保证分类的科学性,做到既不重复,又不遗漏,是求解此问题的关键,限于篇幅,不再赘述. 视角3 特值验证,小题速解. 解法5观察选项与lnx无关,不妨设f(et)=0,则e3t-ae2t+et+1-t=0. 而a=0时,f(x)=x3+ex-lnx, 又ex>lnx,此时f(x)>0,无零点,不符合题意,排除选项D. 故选B. 评注作为选择题,为了节约考试时间,我们期待小题能小做,速战速决,所以结合题设及选项的结构特征,巧妙换元,特征值可排除错误选项,进而快速找到正确选项.这也需要学生有扎实的功底,在较短时间内发现非正确项的破绽. 题1(2016年全国Ⅱ卷第21题第(1)问)已知函数f(x)=(x-2)ex+a(x-1)2有2个零点.求a的取值范围; 题2 (2017年全国Ⅱ卷第21题第(2)问)已知函数f(x)=ae2x+(a-2)ex-x.若函数f(x)有两个零点,求a的取值范围. 通过对此题多种解题方法的探究和比较,能很好地提升学生分析问题和解决问题的能力,逐步培养学生的核心素养,提升学习效率,让学生所学的知识系统化.另外,分离变量、分离函数借助于数形结合是突破此类题的关键,尤其是曲线与直线相切地恰当使用.可以说,题目从知识立意、能力立意向价值引领、素养导向的转变,很好地体现了试题的甄别功能.因此,我们的教学,绝不能够仅仅停留在刷题的层面,一定要在能力和素养上下功夫.
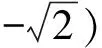

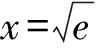













4 高考链接

