深度教研之学情的整体分析

林志辉　吴芳芳

［摘 要］学情的整体分析，是运用科学的方式全面、深刻地把握学生的知识起点及经验起点，进而以学定教，切实提高课堂教学实效。文章围绕核心问题“如何在单元视角下进行学情整体分析”开展研究，以SOLO分类理论助力分析，以“二·三”式学情整体分析模型精准把脉，以数据实证对话深度学习，进行学情整体分析的研究。通过此研究，教师可以更准确地了解学生的学情，调整教学策略，提高教学效率，为课堂教学研究提供新的研究范式参考。

［关键词］单元视角；学情整体分析；SOLO分类理论

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）35-0008-04

在小学数学教学中，学情分析是一项关键的研究工作。通过全面观察和分析学生的起点、难点和拐点等，从而教师能更好地了解学生的学习状况，从而制订个性化的教学策略，以提高教学效率。下面将介绍如何全面、精准和深入地对学生的学习情况进行分析，从而判断学生已有、能有和想有的情况。

一、思考：基于SOLO分类理论进行学情整体分析

教学的转型应从以教师的“教”为主向有效促进学生的“学”为主转变，而学情分析是这一转型过程中的关键因素之一。如果教师在进行学情分析时出现“拿来主义”和“经验主义”的趋势，缺乏对具体教学情境中学生个体学习状态的科学分析，缺乏对学情分析的思维水平层次性和深度性的认识，就会导致学情分析形同虚设，难以促进教学的有效实施。因此，应基于SOLO分类理论进行学情的整体分析。

1.SOLO分类理论

SOLO （ Structure of the Observed Learning Outcome） ，被译为“可观察的学习结果结构”，是指学生在回答某个问题或完成某项任务时所表现出来的思维结构。SOLO分类理论将学习过程分为五个结构层次，分别是前结构层次、单点结构层次、多点结构层次、关联结构层次和抽象扩展结构层次，这些层次反映了学生在问题解决和思维发展方面的不同水平和能力。

在前结构层次，学生无法解决问题，或仅能提供混乱的答案，缺乏系统性的思维和解决问题的能力。

在单点结构层次，学生能够找到解决问题的思路，但只依靠一点论据就得出了答案，缺乏整体性的思维和综合判断的能力。

在多点结构层次，学生能够从不同层面出发寻找问题的最佳解决方法，但在思路的整合与归纳方面仍有困难，获得的信息分散且支离破碎。

在关联结构层次，学生能够找到更多的解题思路，并能够将这些思路进行整理归纳，形成一个有机的整体，还能够将多个事件联系起来，解决较为复杂的问题并检查错误或矛盾之处。

在抽象扩展结构层次，学生能够将结构整体进行归纳，形成基本的理论体系。这个层次的学生具有较强的钻研和创造精神，能够进行高层次的思考和创新。

2.学情整体分析的内涵

学情的整体分析对理解学生、设计教学路径以及实施教学都至关重要。根据数据进行的学情分析可以从知识起点、经验起点和困惑迷思三个方面开展。知识起点指的是学生在学习某一内容之前已经掌握的知识，以及大多数学生学习该内容的一般逻辑顺序。经验起点指的是学生在学习某一内容之前所具备的观察、操作和思考经验。困惑迷思指的是学生在学习过程中普遍或个别表现出的学习难点。

通过这样的分析，教师便可以寻求跨越知识序和认知序之间的学习路径。这一学习路径，既要满足整个班级学生的整体需求，又要关注学生的个体差异，以确保每个学生在课堂中都能获得主动的发展。最后，课后评价若能与之前的学情分析形成呼应，教师就可以更加科学地追踪和量化学生的思维发展水平，从而提高教学的准确性。

二、建构：“二·三”式学情整体分析模型

依据上述分析发现，SOLO分类理论与学情的整体分析具有吻合之处，能够作为学生不同阶段学习情况的分析工具。因此，笔者借助SOLO分类理论，确定了二項三种分析模型，即“二·三”式学情整体分析模型：单项单类直接式分析、单项多类推进式分析、多项并进式分析。

1.单项单类直接式分析

单项单类直接式分析是指基于单项核心素养，借助SOLO分类理论对学生的思维水平进行划分。对思维水平进行划分后，分析学生的一次作答就能快速判断学生的现实基础、活动经验、思维水平，从而确定学生在学习中存在的模糊区与进阶区的断层处，并拟定相应的学习路径。

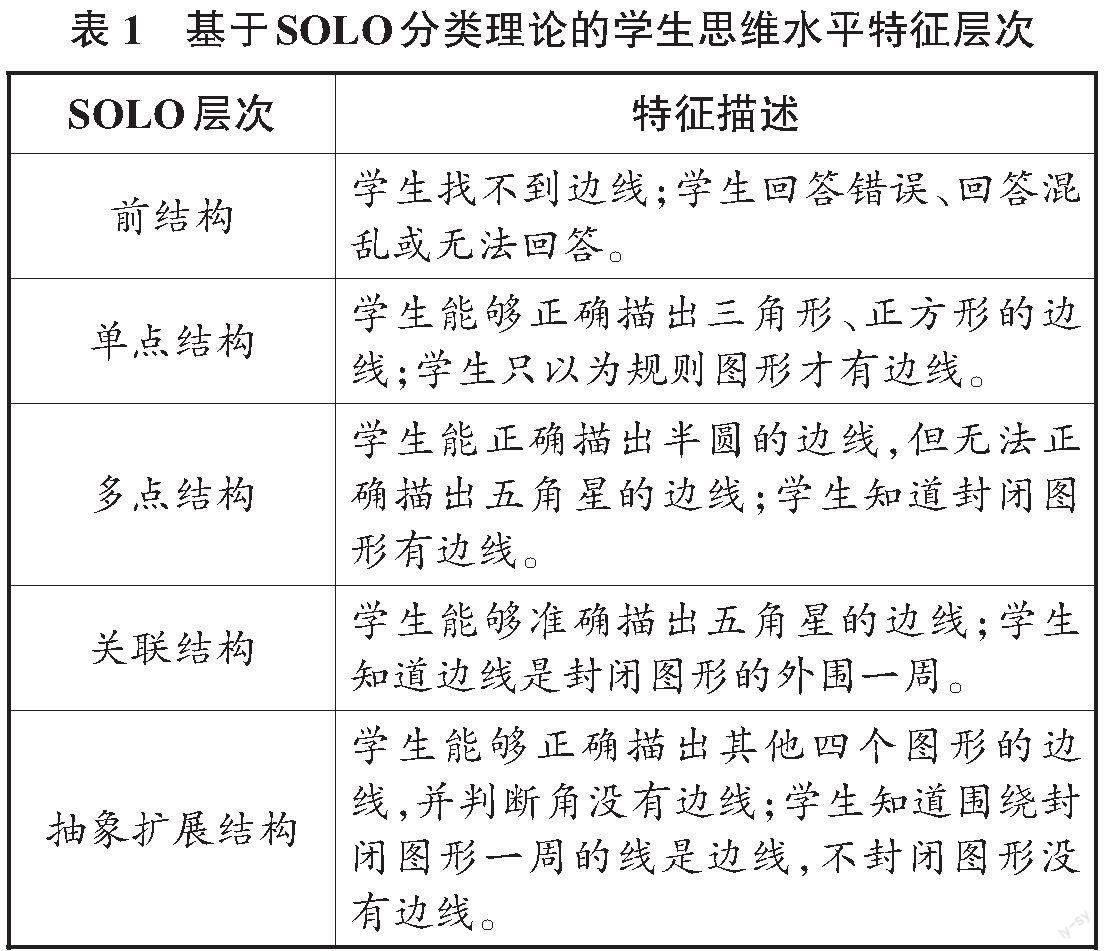
以三年级上册“周长的认识”一课为例。通过内容的整体解读，可确定“边线”为本节课的切入点，再依据SOLO分类理论将学生的思维水平进行划分（见表1），以期掌握学生学习周长概念前的认知理解水平。

基于上述思维层次的划分，笔者设计了“周长的认识”的前测单，并以某小学43名学生为研究对象进行前测。以学生思维水平特征层次划分为依据对前测结果进行分析，发现有53.3％的学生的思维水平仅停留在对基本规则图形的边线概念的认识上，36.7％的学生知道边线是围绕图形一周的线，而仅有10％的学生能够指出不封闭图形没有边线。这表明学生对面与线的概念的认识存在混淆。基于这些调查结果，可以确定学生对边线的理解非常模糊。因此，笔者将本节课的知识起点确定为学生对边线的理解存在模糊性，并设计相应的学习路径（如图1）。

2.单项多类推进式分析

之所以进行单项多类推进式分析，是因为在对单项核心素养进行分析时发现，学生在同一水平层次中呈现不同层级的抽象程度，所以需进行推进式分析以更精准地判断学生的真实水平。

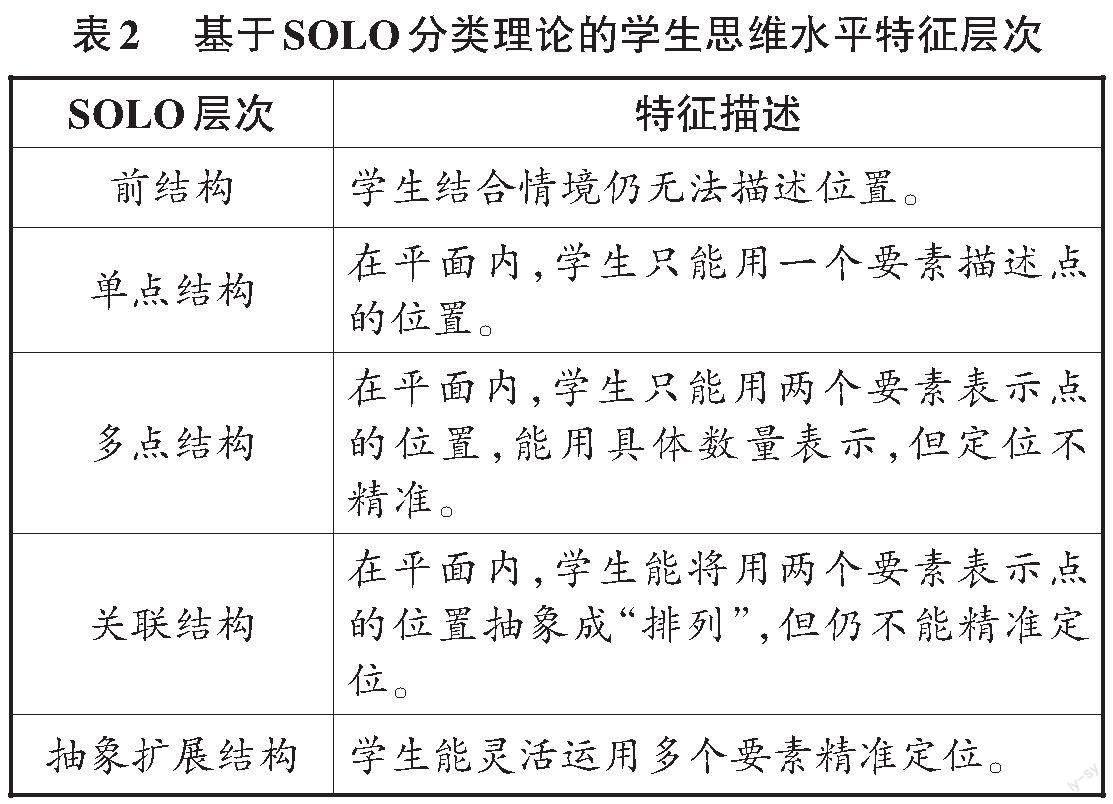
以人教版教材五年级上册“用数对确定位置”为例，本课主要围绕“空间观念”开展教学。以“用几个要素确定平面上的点”进行SOLO分类理论思维水平层次划分（见表2），以期掌握学生学习数对概念前的认知理解水平。

依据上述思维层次划分时，会有“处于同水平层次但其他类别能力处于不同程度”情况的存在，需要进一步划分以提取学生的真实水平。比如，在处于多点结构层次学生的作品中可以看到学生存在两个抽象程度：抽象程度1是把列抽象为数字4，行以具体量4.7 cm来表示；抽象程度2是行和列分别用4.7 cm、7.8 cm这样的具体量来表示确定位置。（见表3）

可见，这是两类不同水平的学生，但是在基于SOLO分类理论的思维水平特征层次划分中，都是“能从两个要素表示点的位置，用具体数量表示，但定位不精准”。

基于此，笔者把本节课学生的整体情况依据“已有、能有、想有的情况”进行分析，从而得出，学生已有的是“从两个方向用具体的量描述平面上点的位置”，想有的是“能灵活运用多个要素精准定位”，能有的是“在平面内，能将用两个要素表示点的位置，抽象成用数表示”。而在“能有的”中，因抽象程度的不同，易有的是能用具体量表示，而难有的是抽象成两个数表示。

如上，相较于单项单类直接式分析模型，单项多类推进式分析模型能更深入、更细致地定位学生在同一SOLO类型下的不同层次，更精准地助力课堂教学，进而让教师更关注学生多元化思维的培养。

3.多项并进式分析

多项并进式分析，是指知识链中涵盖多个重要核心素养的培养，需要多次借助SOLO分类理论对知识点对应学生不同素养的培养进行思维水平层次划分，依据不同素养水平层次设计相应的前测试题，从而找寻相应素养的模糊区。

以人教版教材五年级下册的“图形运动（三）解决问题”为例，这一内容旨在培养学生的推理能力和空间观念。为此，笔者设计了两份前测单，以检测学生在推理能力和空间观念上的水平，并两次对SOLO水平划分进行分析（见表4、表5）。

针对学生的实际情况反映出的知识起点与经验起点，笔者设计了两个核心环节，旨在提高学生的推理能力和发展学生的空间观念，让教学更有深度、广度、角度，让学生的学习更深刻、更清晰、更全面。

以上便是“二·三”式学情整体分析模型，而笔者主要提取以下三个学情整体分析要点：要点一，分析学生的知识起点，为教学设计提供依据；要点二，调查学生的经验水平，为学生的学习方法提供支撑；要点三，对比学生认知顺序和知识编排顺序之间的不同，更精准地设计路径。

三、反思：单元视角下学情整体分析的效能

《义务教育数学课程标准（2022年版）》特别强调了“教—学—评”的一致性。笔者借助SOLO分类理论，通过“把脉学情，追踪课堂，反馈课后”，实现从数据精准到教学精准，从实证分析到教学改进，从深度对话到深度学习的转变，促进小学数学课堂教学的发展。

1.从数据精准到教学精准

关注学生的立场，基于单元整体视角进行内容的整体解读，提炼核心要素，并基于SOLO分类理论对数据进行分析，从而准确把握学生的思维水平层次。在精准把握学生的思维水平层次后，再设计以“大问题、大环节、大活动”为模板的学习路径，力求让教师的教学更精准，学生的学习更全面、合理、清晰、深刻。

2.从实证分析到教学改进

SOLO分类理论强调了“可观察”的特点，即观察和评价学生在特定場合中展示的关于某一主题的学习结果。因此，学情的整体分析应该对应某个主题的思维水平层次分析。教师的教学认知，需要从一节课向一类课转变，从关键点向关联网转换，从量化向提质转变，从而让教学更具高度、广度和深度。

3.从深度对话到深度学习

学情的整体分析是与学生的多次深度对话相结合的。教师通过使用数据和工具进行科学的思维水平层次分析，将学情整体分析与评价整体反馈相结合，调整知识链的学习路径，能提出更加结构化的学习目标，帮助学生更科学、系统、有逻辑地学习。从深度对话到深度学习，能使学习具有“普惠”的效能，从而突出深度学习的重要性。

综上所述，笔者借助SOLO分类理论，形成“二·三”式学情整体分析模型，从数据分析到精准教学，把脉学生学习困难点及拐点，找寻模糊区，再通过实证分析，改进教学，助推学生到达学习区，进而将深度对话转变到深度学习中来。

［ 参 考 文 献 ］

[1] 张恩.SOLO分类评价理论在数学教学中的应用［J］.新课程，2021（28）：150.

［2］ 钱月萍，俞昕.由“量”向“质”的跃进：SOLO 理论指导下数学教学的实践尝试［J］.中学数学研究（华南师范大学版），2014（21）：4-7.

［3］ 罗晓燕，李佳，袁萍等.SOLO 分类理论与学习进阶比较研究［J］.课程教学研究，2021（1）：12-17.

［4］ 孔雪峰.学情分析：走进小学生数学学习的真实世界[J].小学数学教育.2023（10）：20-22.