基于SOLO分类理论的小学数学习题教学新探索
鲍善军 郑书娟
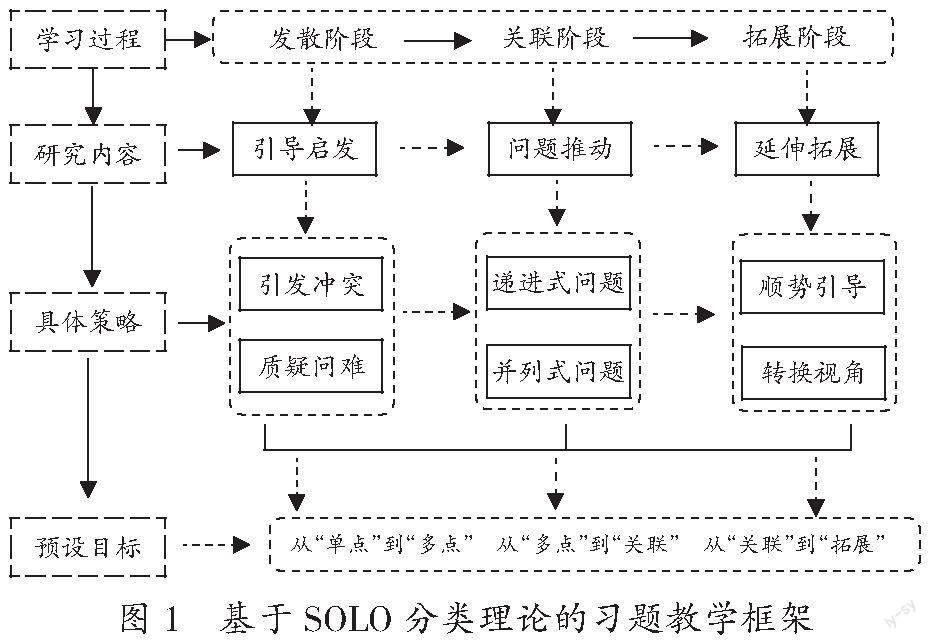
[摘 要]根据SOLO分类理论,学生的数学理解层次从低到高分为五个水平。小学数学习题教学分为发散、关联和拓展三个阶段,以促使学生思维水平按“单点结构—多点结构—关联结构—抽象拓展”逐步发展至高阶思维水平,真正提升学生的问题解决能力,促进学生数学核心素养的内化生长。
[关键词]SOLO分类理论;习题教学;高阶思维
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)35-0058-03
一、小学数学习题教学现状
习题教学不仅有助于学生巩固知识,而且能够促进他们形成系统的问题解决方法,并形成高阶思维,提高综合应用知识的能力。然而,笔者发现在实际的习题教学中存在教学内容零散、教学目标浮于表面、教学活动单一等问题。
首先,教学内容零散。习题之间缺少逻辑关系和系统性,教学时只有一连串的讲解和练习,忽略了习题间的内在关系。对于简单的习题学生完成后教师直接批改,而对于稍微复杂的习题教师则反复强调,处理得过于细致。
其次,教学目标浮于表面。在讲解习题时,教师往往只关注问题本身,没有充分利用素材进行深入讲解。教学只在解决问题的表面徘徊,忽视了高层次思维能力的提升。过分强调解题技巧,而未能深入探讨问题的本质,也忽视了学生分析、联想和抽象思维能力的培养。
最后,教学活动单一。未能发掘习题背后的深层价值,学习活动缺少探究和发现的环节。过分关注问题的结果,导致学生在解题和订正的过程中反反复复,没有数学思维和解题经验的提升。
二、基于SOLO分类理论的习题教学架构
依据曹培英老师的观点,基于SOLO分类理论及可观察的学习结果,学生数学理解层次从低到高可分为前结构水平、单点结构水平、多点结构水平、关联结构水平和抽象拓展结构水平。
基于SOLO分类理论,习题教学分为发散、关联和拓展三个阶段(如图1),通过梯度化呈现,促进学生对知识之间的关联性的理解,实现“学一题、透一点、通一类”的学习目标;通过进阶式教学,引领学生积累问题解决的经验,发展数学核心素养。
三、基于SOLO分类理论的习题教学策略
1.引导启发:思维水平从“单点结构”走向“多点结构”
学生的思维活动是带有明显主观倾向的情意认知过程,教师教学时需要给予学生熟悉且具有引导性的启发,来促进他们从不同角度思考问题,用不同路径解决问题。
(1)引发冲突,以劣构性问题激活思维因子
从学生的认知经验入手,以劣构性问题使学生处于“悱愤”状态。将原有题目进行改编,删减或增加条件,激发学生思考,从而促进学生在解题的过程中发展多样化的认知。
【案例1】改编问题“张老师花48元买6本同样的笔记本,每本笔记本多少元?”
给出条件不足的问题“张老师花48元买同样的笔记本,每本笔记本多少元?”,让学生在此基础上增加合适的条件,并解决问题。学生提出的问题有“张老师花48元买2本同样的笔记本,每本笔记本多少元?”“张老师花48元买2本同样的笔记本,还剩8元,每本笔记本多少元?”。
教师也可以增加条件,得到新问题 “在文具店,张老师花了48元,李老师买6盒铅笔所花的钱比张老师花的钱多12元,每盒铅笔多少元?”
通过补充条件并解决问题,激发学生思维,促使学生主动思考、分析,考虑多方位知识,将相关的知识进行整合,促进学生多元认知。
在補充条件的过程中,学生需要将知识有效地组合在一起。这样可以激发学生的思维潜能,促使他们积极地思考和分析,并将相关的知识联系起来进行整合,推动学生认知的多元化并深化思考。
(2)质疑问难,以开放性问题点燃思维火花
教师要给学生提供质疑问难的空间,引导学生自我提问并解决问题,使学生在反思中主动探究。探究的问题应具有开放性,促进学生思维不断发散,从不同路径去思考或解决问题,促进思维的多点提升。
【案例2】教学“多边形内角和”
教师提出问题“三角形内角和是180°,四边形内角和是多少度呢?”,让学生动手画四边形并求所画四边形的内角和。学生完成后,引导学生研究五边形、六边形、七边形等,从中发现规律。然后,用问题“有一个五边形,沿直线剪一刀剪去一个角,得到一个新多边形,可以怎么剪,新多边形的内角和可能是多少?”激发学生的创造性思维。
用“多边形的内角和怎么计算”“五边形剪去一个角,得到的多边形内角和可能是多少”等开放性问题,促使学生多角度思考,形成多元认知。
2.问题推动:思维水平从“多点结构”迈入“关联结构”
将若干个核心问题组成递进式问题链,能串联知识脉络,将学生的思维引向深处;组成并列式问题链,能拓展学生思维,促进学生思维的发散,驱动学生自主思考、探究和表达,使得学生对已有经验形成结构化认知,重新建立知识体系。
(1)递进式问题,将学生思维引向深处
以数学核心知识为统领,充分挖掘习题背后的数学思想,并通过递进式问题链关联知识脉络,促使学生经历知识串联、问题解决的过程,发展学生的数学思维。
【案例3】教学“长方形面积和周长的关系”
问题1:用24米长的线段围成一个长方形,能怎么围?
问题2:画出你想到的长方形,计算面积并观察,长方形面积有什么变化规律?
问题3:为什么会有这样的规律?
教学“长方形面积和周长的关系”时,教师需要创设具体情境,并挖掘涉及的知识点及其价值,以设计问题链引导学生探索周长相等情况下面积的变化规律。案例中的三个问题层层深入,引导学生串联长方形周长和面积知识,整体建构,使学生的思维向纵深发展。
(2)并列式问题,使学生思维更广阔
条理清晰的思维建立在结构化的知识之上。利用一系列问题唤起学生对知识的记忆,并通过比较、总结和抽象等思维活动将这些知识结合起来,有助于学生构建知识体系。这种方法不仅能促进学生在学习同一主题的不同内容或方法上对知识的理解与融合,而且还能拓宽学生的思维。
【案例4】习题“笼子里有若干只鸡和兔,一共 8 个头、22 条腿,鸡和兔各有几只?”
问题1:用表格能列出所有情况吗?
问题2:用画图的形式能将题意表示清楚吗?
问题3:你能根据所画的图列出算式吗?
问题4:这些方法有什么联系吗?
这几个问题能促使学生借助三种方法进行探究,促进深度思考和理解,从而融会贯通方法,还能拓宽思维。
3.延伸拓展:思维水平从“关联结构”跃至“抽象拓展”
具有创意性的联想和问题解决策略,对学生认识、理解和重构知识大有裨益。教师要指引学生沿着已有的知识脉络去类比和推广,且转变不同的思考视角,进一步提出衍生问题。这种方法能鼓励学生跳出常规的思维模式,从而延展思维的“长度”,使得他们的思维触角能够向更远处伸展。
(1)顺势引导,以拓展性问题拓宽视野
学生能否在探究、拓展与发现等学习活动中打破原有认知,重建知识体系,关键在于问题的设计及学生是否具有审辨式思维。因此,教师要设计拓展性问题,以引导学生发现新知,拓宽视野。
【案例5】教学“平均数的再认识”
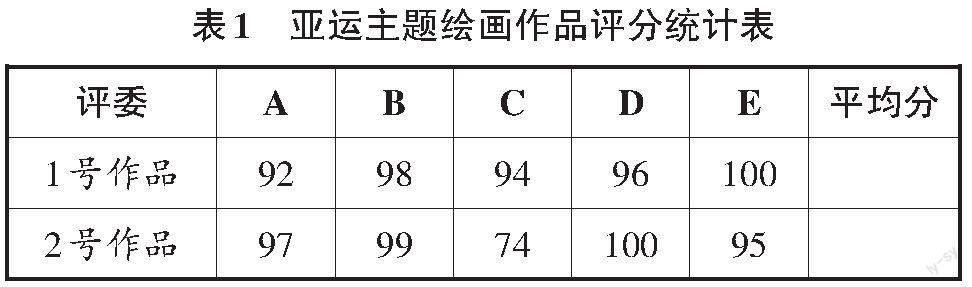
教师出示表1,并提问:“表中是五位评委对亚运主题绘画作品的评分。根据评分,哪幅作品胜出?”
若学生回答1号作品,教师可引导:“作品2的平均分被评委C的74分拉低了,直接算平均数的评价方法失之偏颇,去掉极端数据后再计算平均数似乎更合理。”接着以图说理,通过多媒体直观呈现平均数受到极端数据影响的变化,使学生体会平均数的敏感性,明白“计算平均分时去掉一个最高分和一个最低分”的原因,促进学生对平均数的合理选择与灵活应用。
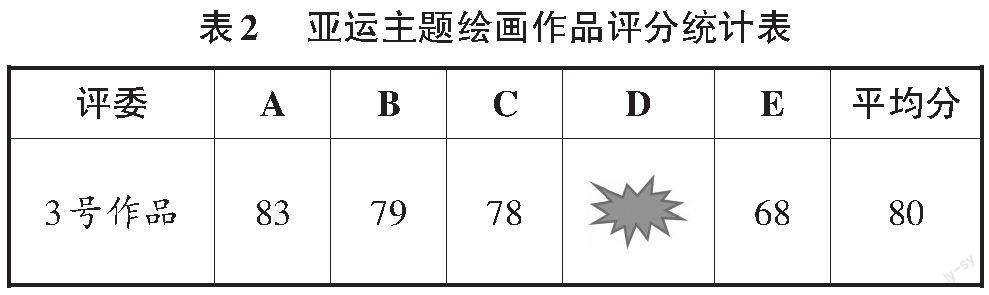
教师接着出示3号作品的评分统计表(见表2)并提问:“评委D的评分不小心被墨汁覆盖了。想一想,已知去掉一个最高分和去掉一个最低分后,平均分是80分,满分是100分,评委D可能打了多少分?①92;②83;③75;④100;⑤88。”
学生在探究与思辨中发现要分“D打的分既不是最高分,也不是最低分”“D打的分是最高分”“D打的分是最低分”三种情况来分析。
最后,教师呈现生活中的实际问题,引导学生思考“平均数是唯一的评判标准吗”“是否还存在其他统计量”等问题。
“平均数的再认识” 的教学目标是加深学生对平均数的认识,特别是在主观评分的场景中加深计算和原理的理解。通过思考“哪幅作品胜出”或“评委D可能打了多少分”等问题,学生不仅巩固了计算平均数的技能,而且学会了在逆向推理时考虑去除了极端值的情况。鼓励学生大胆提问和质疑,使他们打破对平均数的传统理解,认识到平均分并非衡量一组数据的唯一标准,扩展了他们对数据分析的认识。
(2)转换视角,以破势性问题打破思维定式
学生初步建立的知识结构常常是顺向的、固定的,缺乏灵活性、动态性。针对认知经验设计破势性问题,有助于学生转换思考视角,打破思维定式,另辟蹊径,创造性地解决问题,实现数学思维的再延伸。
【案例6】教学“长方形周长与长、宽的关系”
教师让学生探究问题“用16张边长为1分米的小正方形拼长方形,怎么拼才能使拼出的长方形周长最短?”,学生得到长方形长和宽的长度分别是1分米和16分米、2分米和8分米、4分米和4分米(正方形),对应的周长分别是34分米、20分米和16分米,其中,拼成正方形时周长最短。
教师接着利用问题“如果用36个小正方形去拼呢?”引导学生有序思考。学生用表格记录(见表3),发现还是拼成正方形周长最短,验证了规律,巩固了认知。
教师提问:“1个正方形可以平均分成3个周长都是8厘米的长方形,原来正方形的周长是多少?”学生按照正方形周长公式计算,教师追问是否有其他方法,并把条件转化成“用三个周长是8厘米的长方形拼成一个正方形”,引导学生从另一个角度去思考问题,有利于学生打破思维定式,实现思维的再生长。
这几个问题涉及周长的变化规律,让学生在解决问题的过程中巩固认知、提升能力。
实践证明,基于SOLO分类理论的习题教学能帮助学生学会用联系的观点思考问题,积累解决问题的思维经验,形成优良的认知结构。一线教师只有持续研究与实践,方能通过习题教学逐步发展学生的高阶思维水平,真正提升学生的问题解决能力。
[ 参 考 文 献 ]
[1] 彼格斯,科利斯.学习质量评价:SOLO分类理论(可观察的学习成果结构)[M].高凌飚,张洪岩主译.北京:人民教育出版社,2010.
[2] 鲍善军,朱曙光.“一题一课”的教学价值、设计与策略[J].教学月刊小学版(数学),2022(Z2):12-16.
[3] 鲍善军,朱曙光.基于SOLO分类理论的“一题一课”教学设计与实践[J].教学月刊小学版(数学),2021(11):35-39.
[4] 鄭书娟.放大过程,让思维向更深处漫溯:三年级“拼图与周长”教学实践与思考[J].小学教学参考,2021(23):55-56.

