顾及地表散射贡献与多基线参数线性相关性的PolInSAR植被高反演方法

林东方，朱建军，李志伟，付海强，梁 继，周访滨，张 兵

1. 湖南科技大学测绘遥感信息工程湖南省重点实验室，湖南 湘潭 411201；2. 武汉大学测绘学院，湖北 武汉 430079； 3. 中南大学地球科学与信息物理学院，湖南 长沙 410083； 4. 长沙理工大学湖南省公路先进建养技术国际科技创新合作基地，湖南 长沙 410114； 5. 辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000

植被高度是反映森林植被生长状态的重要物理参数，同时也是地上生物量、蓄积量、碳储量以及林下地形估算的重要输入参数，对于气候变化、生态林业、环境保护、灾害评估等科学研究具有重要意义[1-4]。此外，大范围、高精度地获取森林植被高度信息也是森林资源保护与管理的重要任务之一。

极化干涉合成孔径雷达(polarimetric interfero-metric synthetic aperture radar，PolInSAR)技术，继承了InSAR技术全天时、大范围对地观测的优点[5]，同时通过引入极化测量，丰富了观测信息，具备区分森林冠层及地表散射贡献能力，已被视为大范围植被高度信息获取的重要技术[6]。要从PolInSAR观测数据中反演植被高度，需建立合理的物理模型以关联观测数据与植被高参数。文献[7]提出的随机地体二层散射(random volume over ground，RVoG)模型是目前最为常用的物理模型，该模型假设植被散射场景为雷达波不可穿透的地表层以及垂直向均匀分布的植被层，有效建立了极化复相干性与植被参数之间的函数关系[8]。基于该模型，文献[9]提出了反演植被参数的六维非线性迭代方法，成功解算出了模型中的地表相位、植被高等参数。文献[10]考虑地形坡度影响，提出了顾及地形坡度的植被高反演迭代解算方法。然而，植被高反演函数模型被证实存在不适定(秩亏与病态)问题，迭代法依赖于参数初值的可靠性，容易陷入局部收敛[11]。鉴于此，文献[12]利用RVoG模型的几何特性，提出了三阶段反演算法，该算法将植被高反演分成地表相位估计、纯体相干性估计及植被高估计3个阶段，无须模型参数初值，是目前较为稳定且应用较为广泛的方法，在不同森林区域得到了验证[13-19]。然而，由于单基线观测信息的不足，三阶段算法在纯体相干性提取过程中需假设某一体散射占优极化状态无地表散射贡献，该假设导致植被高反演结果存在一定偏差，限制了植被高反演精度，尤其稀疏植被区以及长波SAR观测等地表散射贡献较大情形。引入多基线数据联合解算，理论上可有效降低先验假设引起的参数估计偏差。鉴于此，文献[20]提出利用PolInSAR相干统计特性建立判断指标，筛选最优基线反演植被高度。文献[21]提出引入少量LiDAR数据，采用智能学习算法筛选最优基线。通过引入判断指标或外部数据对多基线进行筛选，可实现植被高反演精度的提高，但该方式仅是将不同单基线的反演结果进行了比较综合，本质上仍采用单基线进行反演，未能充分利用多基线的观测信息。文献[22]提出了植被高反演复数平差法，综合利用多基线观测数据，弥补单基线观测信息的不足，在不同观测条件下成功反演出植被高度[23]。然而，由于多基线模型部分参数间存在近似的线性相关关系，导致多基线观测构建的函数模型存在病态问题[24-25]，因此模型参数估计方差较大，植被高反演精度依赖于病态问题影响程度，从而限制了该方法的植被高反演精度与稳定性。

引入多基线观测数据，有助于实现地体幅度比参数的反演，降低无地表散射贡献假设引起的植被高反演偏差。然而多基线反演模型的病态性严重限制了模型参数的反演精度。引起多基线模型病态问题的关键在于地体幅度比参数与植被高、消光系数等模型参数之间的近似线性相关性，若能准确反演地体幅度比参数，则有助于削弱病态问题影响。鉴于此，本文基于均方误差理论分析病态问题对地体幅度比参数估计影响，利用正则化方法处理病态问题，并基于均方误差最小准则联合多基线信息反演地体幅度比参数，获得地体幅度比参数有效可靠估值；而后，利用地体幅度比参数估值重估多基线纯体相干性，基于最小二范估计准则融合多基线纯体相干性信息反演植被高度，从而提高植被高反演精度与稳定性。

1 RVoG模型与植被高反演方法

1.1 RVoG模型

文献[7]提出的RVoG模型是目前应用最为广泛的相干散射物理模型，该模型将植被散射场景描述为雷达波不可穿透的地面层与垂直向均匀分布的植被层。模型有效建立了极化复相干性与植被参数之间的函数关系。具体表达为

(1)

式中，ω表示极化散射状态；γ(ω)为对应于极化状态ω的复相干系数，为已知观测值；φ0表示地表相位，为未知参数；μ(ω)表示地体幅度比，与极化状态有关，为未知参数；γv表示纯体相干性，与植被高参数相关联。γv具体表达为

(2)

式中，σ表示消光系数，为未知参数；θ表示主影像雷达入射角，为已知值；hv表示植被高参数，为未知参数；kz表示垂直向有效波数；kz可由式(3)计算得到

(3)

式中，Δθ为主副影像入射角差值；λ表示雷达波长。

1.2 植被高反演三阶段算法

受观测信息不足限制，利用单基线数据反演RVoG模型参数，常出现不适定问题，难以获得模型参数的可靠估值。鉴于此，文献[12]基于RVoG模型的几何特性，提出了三阶段反演算法，将模型参数反演分三阶段进行。

(1) 地表相位估计。在RVoG模型几何条件下，单基线不同极化状态的复相干系数在复平面内呈直线分布，利用两种以上极化状态复相干系数，即可在复平面内拟合相干直线，得到直线与复平面单位圆的两个交点。而距离体散射占优极化状态复相干系数(如HV或PDHigh)较远的交点即为地表相位所在点，由此反演出地表相位参数。

(2) 纯体相干性估计。三阶段算法假设某一体散射占优极化状态的复相干性(如PDHigh)仅有微弱的地表散射贡献，则认为该极化状态下地体幅度比为0，而后利用已确定的地表相位参数结合式(1)即可估计出纯体相干性。

(3) 植被高估计。纯体相干性中仅包含消光系数与植被高两个未知参数，利用先验信息设定消光系数与植被高参数上下界，采用二维查找表法基于最小范数准则解算出植被高参数与消光系数估值

(4)

1.3 植被高反演多基线分步解算方法

三阶段算法假设体散射占优极化数据地体幅度比为0，从而实现纯体相干性以及植被高参数的估计。然而，用于植被高反演的长波SAR信号具有强穿透能力，地表散射与体散射往往混合在所有极化状态中，难以找到无地表散射贡献的极化状态[24]。因此，通过假设地体幅度比为0解算的植被高参数存在一定偏差。

引入多基线观测数据，可有效补充观测信息，改善单基线模型参数反演不适定问题。但常规三阶段算法难以融合利用多基线观测信息，无法实现地体幅度比参数的估计。本文基于复数平差算法，构建多基线反演函数模型，实现地体幅度比参数的有效估计，而后重估多基线纯体相干性，并基于最小二范估计准则融合多基线纯体相干性信息实现植被高参数的估计。具体步骤如下：

(1) 地体幅度比参数估计。利用多基线地表相位参数相关性，融合多基线地表相位参数。由先验信息可知，地表相位φ0与地表高度hg及垂直向有效波数kz存在关联。在多基线条件下，各基线地表相位参数以及垂直向有效波数不同，但地表高度不随基线变化而变化。由此，可利用已知参数kz将各基线未知地表相位参数表达为同一地表高参数

(5)

据此，基于RVoG模型的多基线平差函数模型可表达为

γj(ω)=f(hg,σ,hv,μ(ω))j=1,2,…,m

(6)

式中，j表示基线数。由(6)式可知，同一极化状态ω下，不同基线观测数据具有相同的地表高度、消光系数、植被高度及地体幅度比。因此，模型中共包含4个未知参数，通过引入两条以上的多基线复数观测数据即可有效补充观测信息，实现地体幅度比参数反演。

依据复数最小二乘估计准则可得[22]

(7)

(8)

(9)

V=AX-L

(10)

式中，V表示残差向量；A为设计矩阵；X为模型参数改正数向量；L表示观测向量，即实部与虚部残余常数。由复数最小二乘估计准则可得模型参数估值

(11)

然而，受多基线观测几何与模型参数相关性影响，设计矩阵A往往存在病态性，严重影响了未知参数的估计精度及稳定性。由式(11)可得参数估值方差为

(12)

(13)

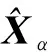
(14)

(15)

(16)

式中，Cα表示参数估值方差-协方差矩阵；偏差向量bα可计算为

(17)

式中，gi为设计矩阵奇异值对应的特征向量。

采用多基线观测数据反演植被参数，G-M模型是确定的，则系数矩阵及其特征向量可为已知值，由多余观测结合系数矩阵可计算正则化估计方差。而后，利用模型参数估值结合式(17)计算模型参数偏差向量，进而可得到各模型参数正则化估值均方误差。分析地体幅度比等模型参数估值均方误差，即可确定各参数估值的有效性与可靠性。由此可知，本文方法的有效性在于地体幅度比参数估值的可靠性。而均方误差大小决定了地体幅度比参数正则化估值的准确程度。常规算法假设地体幅度比为0，由此引起的均方误差为地体幅度比参数真值的二次方。因此，地体幅度比参数正则化估值均方误差小于地体幅度比参数真值二次方，则本文方法优于常规算法，否则无法改善常规算法的植被高反演精度。

(2) 植被高参数估计。植被高参数存在于纯体相干性中，要实现植被高参数的反演，需准确地提取纯体相干性。地体幅度比与地表相位是提取纯体相干性的必要参数，在地体幅度比采用多基线正则化算法估计后，为避免病态性影响，地表相位采用三阶段算法中直线拟合方法进行估计。

多基线同一极化状态下具有相同的地体幅度比参数，不同的地表相位参数，利用地体幅度比参数的正则化估值以及地表相位的直线拟合估值，可从各基线复相干观测中提取各基线纯体相干性

(18)

各基线纯体相干性包含相同的未知模型参数，即消光系数与植被高参数。基于最小二范数估计准则融合多基线纯体相干性信息，建立消光系数与植被高参数最优估计方法，即多基线二维查找表法，进而实现植被高参数的反演

(19)

多基线植被高分布解算方法的具体流程如图1所示。

图1 PolInSAR多基线植被高分步解算方法流程Fig.1 Processes of PolInSAR vegetation height step-by-step inversion method

2 试验分析

2.1 试验数据

为了验证本文方法的有效性，选取BioSAR2008项目数据进行植被高反演试验分析。BioSAR2008是由德国宇航中心实施的全极化SAR卫星应用支撑试验项目。试验区位于瑞典北部Krycklan地区，为典型的北方混交针叶林。森林平均树高18 m，平均生物量90 t/ha。项目采用德国宇航中心E-SAR系统，以重轨干涉方式获取了植被覆盖区多基线P波段全极化数据，用于验证全极化SAR卫星重轨干涉应用潜能。此外，项目实施过程中，瑞典国防研究机构在试验区开展了机载LiDAR测量，获得了试验区的高精度植被高数据，可用于对比分析PolInSAR植被高反演结果。

试验选取空间基线长度分别为16、24和32 m的多基线干涉数据联合反演植被高度，各基线参数信息见表1。

表1 多基线数据参数信息Tab.1 Information of multi-baseline observations

2.2 地体幅度比估计结果

利用3条基线的PDHigh极化数据构建多基线反演函数模型，由3条基线数据可建立6个观测方程，包含地表高、植被高、消光系数及地体幅度比4个未知模型参数。首先，采用三阶段算法解算模型，得到未知模型参数初值；其次，采用正则化方法解算方程，得到未知模型参数的正则化估值。利用模型参数估值估算正则化估计的方差与偏差，进而得到正则化估值均方误差见表2。

表2 模型参数估计误差Tab.2 Estimation errors of model parameters

由表2可知，受偏差影响，地表高与植被高估值均方误差较大，正则化方法难以有效提高两参数的估计精度。但消光系数与地体幅度比参数估值均方误差较小，估值较为可靠，整幅影像参数估值如图2所示。

图2(a)给出了消光系数的估值大小，结合消光系数先验信息可知，消光系数本身较小，尽管其估计均方误差较小，但该误差仍对消光系数估计造成了较大影响，导致参数估值不可靠，其正则化估值可作为参考。图2(b)反映了地体幅度比参数估值大小情况。由图2可知，植被覆盖区地体幅度比参数大小范围为0.4～0.6，而其估计均方根误差为0.046 8，约为估值的10%，估值可靠性较高。相比于三阶段算法将地体幅度比设为0(均方根误差则达到0.4～0.6)，精度得到了显著提升。因此，采用多基线数据结合正则化算法，可获得地体幅度比参数的可靠估值。

图2 消光系数与地体幅度比反演结果Fig.2 Inversion results of extinction coefficient and ground-to-volume ratio

2.3 植被高反演结果

LiDAR测量技术可获得较高精度的植被高度，可作为真值进行对比分析，由LiDAR获取的植被高结果如图3所示。

图3 样地选择Fig.3 Selection of standards

图3(a)为LiDAR植被高反演结果，图3(b)给出了用于对比分析的样地分布情况。由多基线函数模型正则化解法获得的地体幅度比参数以及三阶段法直线拟合获得的地表相位参数重估多基线纯体相干性，进而采用多基线查找表法反演植被高度。此外，为便于验证分析，分别采用三阶段算法、S-RVoG模型常规解法、多基线常规解法，以及多基线常规正则化解法反演植被高度，各方法的植被高反演结果如图4所示。

图4 各方法植被高反演结果Fig.4 Vegetation height inversion results of each method

由图4各方法植被高反演结果可知，植被高估值由左至右存在一定的趋势性，这主要由于SAR系统入射角沿距离向逐渐增大，SAR影像近距端与远距端入射角差异较大，导致垂直向有效波数沿距离向发生变化，干涉图近距端与远距端测高敏感度存在差异，最终导致植被高度反演存在趋势性误差[31-32]。趋势性误差因入射角跨度不同而表现不同，跨度越大则表现越明显。在BioSAR2008全极化SAR试验中，为验证不同入射角对植被高度反演的影响，入射角范围为25°～60°，跨度较大，趋势性误差较为明显。在实际生产应用中，可通过两端重复覆盖观测缓解两端趋势性误差。

由图4(a)可知，三阶段算法的植被高反演结果相比于LiDAR结果存在一定低估，这主要由于三阶段算法假设体散射占优极化状态地体幅度比为0，从而降低了纯体相干性估计精度，导致反演的植被高度偏低。图4(b)为S-RVoG模型下引入地形信息的植被高反演结果，可以看出，尽管反演过程中引入了先验地形信息，但反演结果未有明显改善。这主要因为引入地形信息后，地形先验数据的误差同样引入到模型中，从而影响植被高反演精度，通常情况下植被覆盖区的高精度的地形数据往往难以获得，导致植被高反演结果未得到明显改善。图4(c)为多基线未顾及病态性影响的植被高反演结果，可见在病态性影响下，常规解算方法已难以获得植被高的有效估值。图4(d)为采用常规正则化方法处理病态性影响的多基线植被高反演结果，尽管正则化解法可有效降低病态性影响，但反演的植被高结果相比于三阶段算法仍未见明显改善。主要原因在于常规正则化算法通过引入偏差降低均方误差以提高模型参数的整体估计精度，但正则化算法为降低病态性影响所引入的偏差主要附加在了植被高参数估值上，导致植被高估计精度未有明显提升。多基线分步解法的植被高反演结果(图4(e))较前4种方法有了显著改善，分步解法首先利用多基线数据解算地体幅度比参数，进而重估各基线纯体相干性，相比于三阶段算法设置地体幅度比为0，纯体相干性提取精度得到了明显提升；其次，基于最小二范数估计准则融合利用多基线纯体相干性反演植被高度，反演结果具有更高的稳定性与可靠性。

2.4 植被高反演误差分析

为了量化分析各方法的植被高反演结果，均匀选取了1200块样地进行误差统计，样地分布如图3(b)所示，统计结果如图5所示。

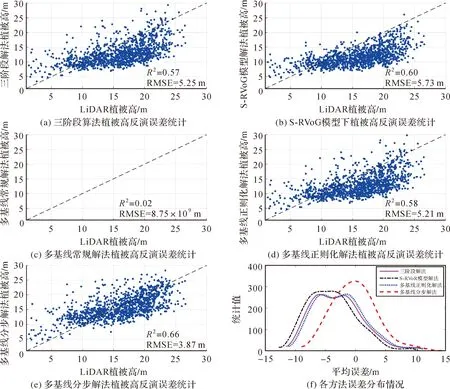
图5 各方法样地植被高反演误差Fig.5 Standards vegetation height inversion errors of each method

对比样地误差统计结果图5(a)、(b)可知，引入地形信息的植被高反演均方根误差未能得到改善，表明低精度的地形信息难以提高植被高反演精度。由图5(c)、(d)可知，引入多基线观测信息后，受多基线模型病态性影响，常规解算方法无法获得有效的植被高参数，常规正则化解法可改善病态性影响，但反演结果受病态问题改善程度影响与三阶段算法具有相近的均方根误差及相关系数，表明多基线常规正则化解法同样未能有效提高植被高反演精度。由图5(e)可知，多基线分步解法植被高反演均方根误差相较于三阶段算法降低了26%，相关系数R2也有明显提高，表明多基线分步解法可有效提高植被高反演精度。比较各方法的误差统计分布情况如图5(f)所示，三阶段算法、S-RVoG模型与多基线常规正则化解法误差分布期望值在-4 m左右，且误差分布范围较广，方差较大；而多基线分步解法误差分布期望值接近于0，分布范围相较于前二者也有所收缩。因此，多基线分步解法在提高反演精度的同时，具有更高的稳定性与可靠性。

3 结 论

受单基线观测信息不足限制，三阶段算法假设体散射占优极化状态无地表散射贡献，进而提取纯体相干性实现植被高参数反演。然而，该假设往往导致植被高反演结果存在一定偏差，限制了植被高反演精度。通过引入多基线观测数据，可有效补充观测信息，有助于实现地体幅度比参数的反演，降低植被高反演偏差。由于多基线模型引入过多的模型参数，受多基线观测几何影响，部分模型参数存在近似线性相关性，导致模型病态，降低了地体幅度比等模型参数反演精度。鉴于此，本文提出了植被高反演多基线分步解算方法。首先，基于多基线数据构建反演函数模型，针对模型中的病态问题，采用正则化解算方法解算模型，获得地体幅度比参数正则化估值，并通过分析模型参数估值均方误差变化，确定可靠的地体幅度比参数估值。然后，利用反演的地体幅度比参数重估多基线纯体相干性。最后，基于最小二范估计准则，融合利用多基线纯体相干性数据，实现植被高参数的反演。试验结果表明，本文方法相比于常规方法有效提高了植被高参数反演精度及稳定性，是一种行之有效的方法。