关联退极化量子信道中qutrit-qutrit系统的量子相干性演化*

董曜 纪爱玲 张国锋†

1) (北京航空航天大学物理学院,北京 100191)

2) (中国科学院大学物理学院,北京 100190)

为探索量子系统的退相干机制寻找延缓退相干的方法,本文研究了关联量子信道中的退相干过程,计算了关联退极化信道中两体qutrit 系统的3 种初态:一种特殊初态、最大相干初态和各向同性初态的范数相干性、相对熵相干性及基矢无关相干性.分析得出的解析结果、数值结果和演化图像可以发现:1)完全关联的信道能最大程度地抑制退相干;2)存在一个与关联度无关的最大退相干时间点,但其退相干的演化行为却依赖着关联度;3)信道的关联可以增强子系统间的相干性.基矢无关相干性遵循的不等式关系也在此系统中得以验证.

1 引言

量子相干性来源于量子力学五大基本原理之一的量子态叠加原理,是量子系统的关键的特征之一及二部和多部量子关联的本质[1].在密度矩阵中,量子相干性表现为矩阵非零的非对角项.量子相干性是经典体系所不具备的一个重要性质,不仅具有重要的理论意义,还可作为量子通信、量子计算和量子计量等新兴技术的物理资源.在过去一些年,特别是Baumgratz 等[2]基于资源学说理论提出量子相干性可以像量子纠缠、量子失协那样视作一种有用的量子资源,并提出了几种量子相干性的度量方法之后,针对体系中量子相干性的研究逐渐增多[3-11],量子相干性测量方法的提出使一些旨在揭示开放系统的退相干机制的研究得以实现,并且文献[12]提出相干性演化方程的因式分解关系.近年来,研究一直在努力寻找能更加灵活操控退相干动力学和产生稳态相干性的方法.此外量子相干性、量子关联和量子纠缠的研究为量子相变等领域提供了新思路[13],还在量子生物学中得以应用[14,15].

虽然量子相干性在许多技术中有非凡意义,但它是一种非常脆弱的物理属性.通常情况下,环境、测量等因素对量子系统产生的影响不可避免,这些影响会造成量子相干性的快速衰减[15],是一类限制量子技术发展的主要障碍.

量子信息处理、传递和衰减的基本方式对应3 种典型的量子信道:相位阻尼信道、退极化信道和振幅阻尼信道[16].在Macchiavello 等[17]提出关联信道的联合概率函数之前,以往的研究都集中在单边信道,或非关联信道的方面,即信道之间不存在记忆效应.但这都不是更普遍的量子信息衰减方式.对更一般的情况而言,信道之间会存在关联,这种关联表现在短时间间隔内连续通过噪声信道的量子比特,信道会对其演化保留一定的记忆效应.

此外,以往研究大多数局限于qubit 系统,但近年来更高维的量子系统逐渐得到更多重视[18].已有研究证明,相较于qubit 系统,维度更高的量子信息单位可以更大程度破坏定域实在论,噪声对其相干性与纠缠等量子资源的影响也更小[18].在量子信道中更高维系统能更加安全地应对窃听威胁,同时为通信提供更大的信道容量与更可靠的信息处理方式.从实验制备的角度看,更高维的纠缠态也能在线性光学系统中实现[19].况且,很多情况下量子信息任务必须要更高维的量子系统才能进行.

本文旨在研究关联量子信道中qutrit-qutrit系统的量子相干性演化,探索退相干机制,希望找到有效方法尽可能延缓退相干过程.

2 量子相干性的测量方法

量子相干性有多种测量方式,如范数相干性、相对熵相干性、基矢无关相干性[20]、相干的鲁棒性等[21],本文主要研究前两种计算较为简便的相干性,以及与体系基矢定义无关的相干性.

l1范数相干性:对于基矢{|i〉}下的密度矩阵ρ其定义为[2,3]

即为密度矩阵所有非对角元的绝对值之和.

相对熵相干性[1-3]:

上述两种量子相干性的度量方法与所选择的系统基矢相关.Radhakrishnan 等[20]借助量子系统下的Jensen-Shannon 离散函数定义了基矢无关的总量子相干性:

其中,I为单位矩阵,d为密度矩阵维度.

在单量子比特的Bloch 球中更容易理解和比较基矢相关的相干性和基矢无关的相干性,二者分别度量的是极化矢量到Z轴的最小距离与到球心的距离,如图1 所示[20].

图1 图中的球为Bloch 球,绿色线段标示的距离衡量的是基矢无关量子相干性,红色线段标示的距离衡量的是基矢相关的量子相干性Fig.1.This is a Bloch ball,the distance marked by the green line represents basis-independent quantum coherence and the distance marked by the red line represents basis-dependent quantum coherence.

Radhakrishnan 等[20]还提出,多部总基矢无关相干性能分解为联合与局域两部分.第一部分联合量子相干性衡量的是存在于子系统之间的相干性.联合量子相干性表示为

其中 πρρ1⊗···⊗ρn,ρi为第i个子系统的约化密度矩阵.

局域量子相干性衡量的是存在于各子系统内的相干性,表示为

三者之间存在不等式关系[20]:

3 关联信道

3.13 种典型的量子信道

信息处理过程中有3 种量子信息衰减典型方式:相位阻尼方式、退极化方式和振幅阻尼方式[16],它们是单量子比特系统超算符的3 种模式,称为量子信道.

相位阻尼此量子信道的作用可用一个作用在A和E直积空间HA ⊗HE的幺正算符表示:

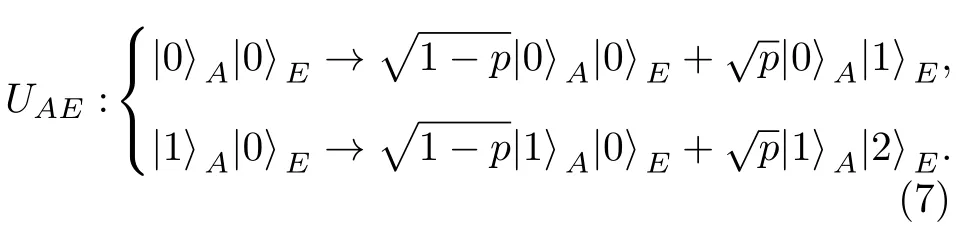
该信道下A态空间的两个基稳定不发生误翻转,但以概率p与环境态纠缠导致环境状态改变.

退极化退极化信道下单量子比特的两个基不绝对稳定,存在3 种基本的误翻转类型,假设这3 种误差发生概率相等,用一个作用在HA ⊗HE上的幺正算符表示[16]:

在该信道下极化矢量收缩为

振幅阻尼振幅阻尼信道可以看作双能级原子高能级发生衰变的简化模型[16],原子与环境的相互作用用如下算符表示:

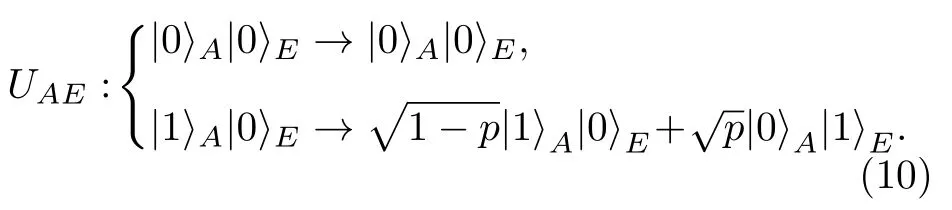
这3 种量子信道都会使密度矩阵非对角元衰减,导致量子体系的退相干.

3.2 关联退极化信道

由n个量子比特组成的系统,如果某噪声信道对通过的每一个量子比特的演化作用完全相同且独立,这种噪声信道完全没有关联性.系统一个初态ρ0在这种信道下线性映射为[17]

完全不关联的退极化信道下Kraus 算符的形式为

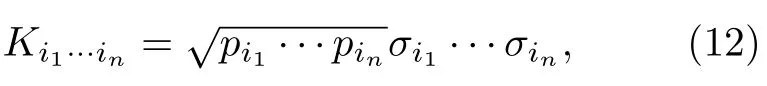
对于关联的量子信道,其联合密度函数为条件概率的形式:

参数μ满足 0≤μ≤1,描述的是信道的关联度,μ0为完全不关联,0＜μ＜1 为部分关联,μ1对应完全关联的信道[17,22].两qutrit 连续通过退极化噪声信道,其量子态演化模型为[20-22]

其中ρ0为初态,Pi,j为联合概率函数,3⊗3 维矩阵元Ei有以下形式[22-24]:

参数:

与信道关联度相关的概率分布函数为:

在退极化信道下Γ为任一量子态向其正交态的衰变率

4 相干性计算

4.1 贝尔态与可分离混态混合成的特殊初态

首先考虑初态是一种特殊混态的情况,此初态是最大纠缠态(贝尔态)与两个可分离混态按一定比例混合成的,表示为

范数相干性该初态下的l1范数相干性演化的解析表达式,如下:

分析这个解析表达式,很容易得到在时间趋近于无穷下的稳态解:

范数相干性随时间演化最终渐近于某定值,此定值与信道关联度有关.在μ1 的完全关联条件下稳态相干性最大,说明完全关联的信道能最大程度抑制退相干.而μ1/9 时稳态下相干性为零,表明该关联度的信道使系统发生了完全退相干.

在演化时间达到Γt2ln9 时(如图2),范数相干性Cl10,即此初态下量子体系的相干性会在固定时间点衰退到0(发生了最大退相干),这个时间与关联度完全无关.

图2 蓝色、红色、绿色、紫色、黑色曲线依次对应关联度μ为1,0.5,1/6,0.1,纵坐标表示范数相干性Fig.2.Blue,red,green,purple and black lines correspond to μ as 1,0.5,1/6,0.1,and Y-axis represents l1 norm coherence.

通过将相干性解析式对时间求偏导还能发现此初态存在3 种与关联度有关的不同演化方式,可分为图3—图5 中的情况讨论.

1)当 1/5 ≤μ≤1 或μ0 时,演化时间在达到范数相干性固定零点Γt2ln9 前相干性逐渐减小,在零点后递增渐近至稳态值,如图3 所示.

图3 关联度满足 1/5 ≤μ ≤1或 μ=0 时第一种演化方式(μ=1).Fig.3.The first caseof evolution when 1/5 ≤μ ≤1 or μ=0(μ=1).

2)当 1/9 ≤μ＜1/5 时,固定零点前与1)相同,相干性随时间递减到零,之后先递增后渐近递减到稳态值,极大值点位于处,极大值为μ2/[7(1-μ)],如图4 所示.

图4 关联度满足 1/9 ≤μ＜1/5时第二种演化方式(μ=1/7)Fig.4.The second case of evolution when1/9 ≤μ＜1/5(μ=1/7) .

3)当 0＜μ＜1/9 时,固定零点前相干性随时间递减到0,此后先递增,再衰减到第2 个零点,极大值点与第2 个零点分别位于:和,第2 个零点后相干性有所恢复,随时间递增到稳态值.如图5 所示.

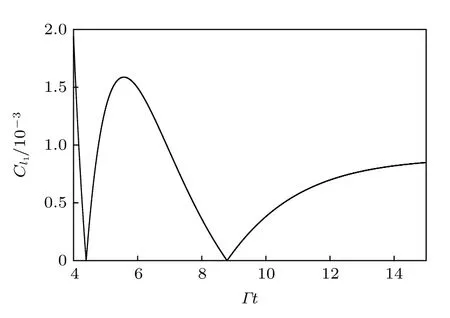
图5 关联度满足 0＜μ＜1/9时第3 种演化方式(μ=1/10)Fig.5.The third case of evolution when0＜μ＜1/9(μ=1/10).

相对熵相干性本文中相对熵相干性的解析求解涉及到九阶方阵的特征值计算,且含参数较多,因此仅研究时间趋近于无穷的稳态下的相对熵相干性和相对熵相干性演化的数值结果.在Γt→∞时:

图6 为稳态时相对熵相干性与关联度μ之间的关系,可得出结论:与范数相干性类似,稳态时仍是完全关联的情况下相对熵相干性有最大值,关联度μ1/9 时相对熵相干性最小为0.

图6 稳态的相对熵相干性随退极化信道关联度的变化Fig.6.The change of relative entropy coherence of the steady state with the correlation degree of depolarizing channels.

分析相对熵相干演化图7 可以发现,其演化规律与范数相干性十分相似,也存在一个固定的零点Γt2ln9.此外也存在3 种演化方式,且3 种演化方式与范数相干性相同,如图8 所示.

图7 相对熵相干性随时间的演化,纵坐标为相对熵相干性数值,蓝色、紫色、绿色、红色和黑色曲线分别对应关联度 μ=1,0.5,1/6,0.1,0 的情况,发现不同关联度下相对熵相干性在同一时间点衰减到0,零点满足 Γt=2 ln 9 .Fig.7.The relative entropy coherence evolving over time,Y-axis represents the value of relative entropy coherence.Blue,purple,green,red and black lines correspond to μ as 1,0.5,1/6, 0.1 and 0.It can be found that the relative entropy coherence decays to 0 at the same time under different correlation degrees,and the zero point is Γt=2 ln 9 .

图8 相对熵相干性在固定零点 Γt=2 ln 9后的3 种演化方式 (a) μ=0 或 1/2 ≤μ ≤1;(b) 1/9 ≤μ＜1/5;(c) 0＜μ＜1/9 (图中依次取 μ=1,1/7,0.1).Fig.8.Three ways of evolution of relative entropy coherence after fixed time point Γt=2 ln 9:(a) μ=0or 1/5 ≤μ ≤1,(b) 1/9 ≤μ＜1/5;(c) 0＜μ＜1/9 (μtakes to 1,1/7,0.1 respectively) .

4.2 最大相干初态

再选最大相干态作为初态,该初态ρ0满足[2]:

即密度矩阵所有元素都为 1/9 .此初态在关联退极化信道下的l1范数相干性解析式为

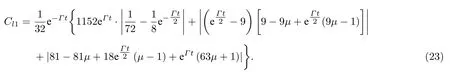
在Γt→∞的稳态条件下,表示为

可以发现对于这种初态,完全关联的退极化信道也能最大程度抑制退相干过程,可参看图9.

图9 最大相干初态的范数相干性随时间演化,纵坐标表示其l1 范数相干性,蓝色、红色、黄色、紫色、黑色曲线分别对应关联度 μ 为1,0.5,0.2,0.1,0 的情况.Fig.9.The l1 norm coherence evolution figure of maximum coherent initial tate,Y-axis represents l1 norm coherence.Blue,red,yellow,purple and black lines correspond to μ as 1,0.5,0.2,0.1,0.

可以看出此初态在演化过程中在相同时间点达到最小值,发生最大退相干,时间点Γt2ln9 与前初态相同,但不同的是在该点的相干性并不一定衰减到0,而是衰减到一个与信道关联度有关的值,即 2μ,只有在完全不关联的情况下才会发生完全退相干的现象.再分别计算此初态在关联度μ分别为1,0.5,0 时的基矢无关总相干性、联合量子相干性与局域量子相干性,如图10—图12 所示,其中C为基矢无关总相干性,Cl为局域量子相干性,CC为联合量子相干性.计算联合量子相干性与局域量子相干性代数和的目的是验证此系统下的相干性的不等式关系.

图10 基矢无关总相干性,联合量子相干性与局域量子相干性演化图像(μ=1,局域量子相干性)Fig.10.The basis-independent quantum coherence,collective quantum coherence and localized quantum coherence evolving over time(μ=1,l) .

图11 基矢无关总相干性,联合量子相干性与局域量子相干性演化图像(μ=0.5)Fig.11.The basis-independent quantum coherence,collective quantum coherence and localized quantum coherence evolving over time(μ=0.5).

图12 基矢无关总相干性,联合量子相干性与局域量子相干性演化图像(μ=0).Fig.12.The basis-independent quantum coherence,collective quantum coherence and localized quantum coherence evolving over time (μ=0).

分析图10—图12 中完全关联,部分关联(关联度为0.5)和完全不关联情况下的基矢无关相干性、联合量子相干性与局域量子相干性计算结果,可以得出的结论是:在完全关联和部分关联的情况下,子系统之间的相干性(联合量子相干性)逐渐增长,且在完全关联信道下其增长更为显著,但在完全不关联的情况下联合量子相干性始终为0,说明量子信道的关联性有助于加强子系统之间的相干性.且在不同关联度下,基矢无关相干性的不等式始终成立.

4.3 各向同性初态

最后选择各向同性态作为初态:

其中|Ψ+〉为前文提到的贝尔态,为最大混态.计算此初态的l1范数相干性得到:

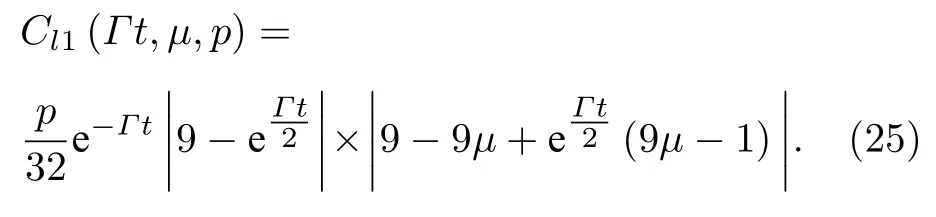
与4.1 节中的范数相干性比较,发现仅是在式中引入了一个比例参数p,说明此初态相干性的演化规律与4.1 节所得出结果完全一样,贝尔态的比例参数仅决定相干性的大小.

5 结论

本文中从双qutrit 量子态中依次选取贝尔态与可分离混态混合的特殊态、最大相干的量子态和各向同性量子态作为初态,研究它们在关联退极化量子信道下的相干性演化,发现完全关联的退极化信道总能最大程度地抑制系统的退相干,可以为实际的量子信息应用提供参考.对于本文中初态与关联信道构成的模型,在一个特殊的时间点Γt2ln9,相干性总会衰减到最小值.对于特殊态与各项同性态,该最小值与关联度μ无关为0,对于最大相干态最小值为与关联度μ有关的量2μ.在研究特殊态时,发现在系统完全退相干时间点后还存在着3 种取决于关联度μ的演化方式.

通过计算第二种初态下的基矢无关相干性,能够得出结论:信道的关联能够增强两体系统下存在于子系统之间的相干性,且相干性的不等式关系始终成立.

最后对比第一种特殊态与第3 种各向同性态,发现两者的相干性演化行为是一致的,比例参数p仅影响各向同性态相干性整体大小,而第一种特殊态的相干性演化与两可分离混态的比例参数α无关.