退相位环境下Werner 态在石墨烯基量子通道中的隐形传输*

张乐 袁训锋 谭小东

(商洛学院电子信息与电气工程学院,商洛 726000)

基于有效低能理论,研究了退相位环境下Werner 态在石墨烯基量子通道中的隐形传输.结果表明,输出态纠缠度总是随着输入态纠缠度的增大而增大,而相应的保真度却正好相反;对于给定的输入态,量子通道中的纠缠越大,输出态的品质就越高.对于石墨烯基量子通道,低温和弱库仑排斥势可以减缓其纠缠资源在退相位环境中的衰减,且温度低于40 K,电子间库仑排斥势小于6 eV 时,输出态的平均保真度可以达到80%以上.这就说明石墨烯材料在量子信息领域中具有潜在的应用价值.

1 引言

量子隐形传态(quantum teleportation,QT)是以量子纠缠作为资源,并结合经典通信将一未知量子态从一个地方传送到另外一个地方的全新通信技术[1].它不仅是一种重要的量子通信方式,而且是发展量子计算[1]和量子网络[2]的基础.自1993年Bennett 等[3]首次提出QT 以来,许多新的量子技术也随之发展起来,如量子中继[4,5]、测量为基础的量子计算[6,7]、量子门的远程传输[8,9]以及无需纠缠资源协助的量子态安全传输等[10].在过去的十几年里,QT 已经在各种各样的物理系统中实现,如光子系统[11-15]、囚禁原子系统[16,17]、原子系综[18,19]、固态系统[20-22]以及IBM Q Experience 在线量子平台等[23,24].2017 年,我国建成了全球首条量子通信“京沪干线”,结合“墨子号”量子卫星实现了天地一体化的广域量子通信体系,并完成了星地间的QT 实验[25].在这些量子系统中,固态量子系统易与现代微纳加工工艺接轨,且大规模可扩展性问题能自然得到解决,是未来发展固态量子计算的重要研究方向.进而固态量子系统中量子信息的传递与存储也引起了人们极大的研究兴趣[26].光子到固态物质的量子态传输已经在光子比特和固态量子存储为基础的实验中实现[20,27].固态物质间的量子态传输也已经在超导量子电路中实现[21].最近,Llewellyn等[28]还在硅基光子芯片间实现了量子隐形传态和多光子纠缠.这些对于发展固态量子计算与量子通信具有深远的意义.然而,由于外界环境的影响,量子退相干是所有量子系统所面临的共同难题.因此,要发展固态量子系统,就必须找到能够保持较长相干时间的材料.

石墨烯[29]中自旋-轨道耦合和精细作用非常微弱,电子自旋能够保持较长的相干时间,因此是非常理想的固态量子材料.为了获得更加优异的电磁学性能,经常把石墨烯裁剪成准一维的结构,即石墨烯纳米带(graphene nanoribbon,GNR).根据边缘结构的不同,常见的GNR 有呈金属性但无磁性的扶手椅型GNR和呈半导体性且有边缘磁性的锯齿型GNR[30-32].目前实验上已经能够制备出高品质的带有两个锯齿端的扶手椅型GNR[33,34].基于有效低能理论[35],Golor 等[36]研究了该GNR两个锯齿端间的磁性关联,结果发现纳米带两端的自旋是相互纠缠的.进一步,Gräfe和Szameit[37]发现石墨烯的边缘几何形状对边缘态中的量子关联演化有非常显著的影响.为了探索石墨烯材料在量子信息领域中的应用,相关学者提出在石墨烯量子点[38,39]、石墨烯纳米带量子点[40]和钒基酞菁/石墨烯/SiC(0001)杂化结构中[41]制备自旋量子比特的方案.基于自旋量子比特,Guo 等[42]在“Z”字形GNR 中设计了一种高效率和高保真度的可扩展量子计算方案.后来,Dragoman 等在理论上提出了在室温条件下实现量子逻辑门的方案和改进的Deutsch-Jozsa 算法[43],并在晶片尺寸的石墨烯基结构上进行了实验验证[44].以上结果均表明石墨烯材料在量子信息领域有潜在的应用价值.

考虑到石墨烯诸多优良的物理特性,且带有两个锯齿端的高品质扶手椅型GNR 已经可以在实验上制备,本文将研究该特殊结构的石墨烯纳米带(special graphene nanoribbon,SGNR)在量子通信方面的应用—在SGNR 构建的量子通道中实现Werner 态的隐形传输.考虑到真实的量子通道总是会受消相干环境的影响,简单起见,本文只考虑退相位环境对量子通道及输出态的影响.通过计算输出态的纠缠度和保真度分析输出态的品质,同时讨论温度和电子间的库仑排斥势对输出态的影响,进而说明该量子通道的鲁棒性,推动石墨烯材料在量子信息领域中的应用.

2 模 型

本文考虑的特殊结构的石墨烯纳米带SGNR如图1(a)所示.Golor 等[36]的工作已经证明,对于带宽W=3 且带长L≥8 的SGNR 来讲,两锯齿端上的自旋粒子间呈反铁磁耦合,有效相互作用的哈密顿量H0可以用海森伯模型描述[36]:

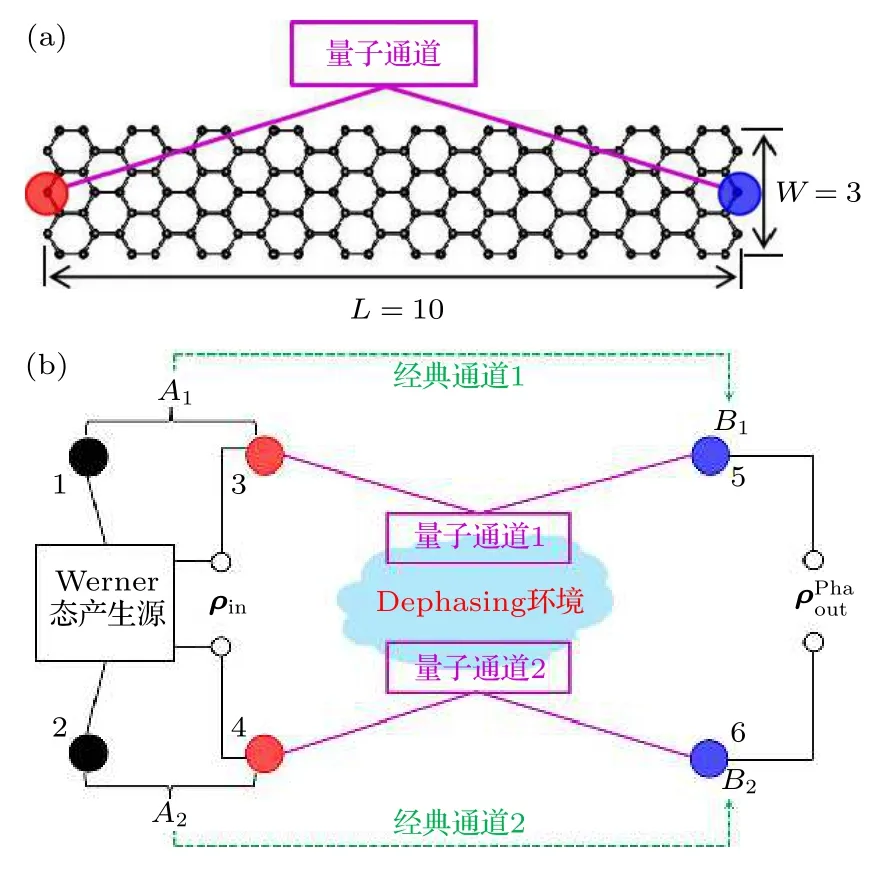
图1 退相位环境下Werner 态在石墨烯基量子通道中的隐形传输原理图 (a) 构建量子通道的特殊石墨烯纳米带(SGNR)几何结构.带长(L)和带宽(W)分别用沿着扶手椅形和锯齿形边缘的六方格子的数目表征.红色和蓝色小球表示一对呈反铁磁耦合的电子自旋,它们就是构建量子通道的物理比特.(b) Werner 态的隐形传输原理图.黑色小球(1,2)表示产生Werner 态的物理比特.量子通道的物理比特分别由两个尺寸完全相同的SGNR 锯齿端上的纠缠粒子对(3,5)和(4,6)承担Fig.1.Schematic illustration of teleporting the Werner state via the graphene-based quantum channels under the dephasing environment:(a) Lattice geometry of the special graphene nanoribbon (SGNR) used to form quantum channels.The ribbon length (L) and width (W) are characterized by the number of hexagons along the armchair and zigzag direction,respectively.The red and blue particles denote a pair of spins with the antiferromagnetic coupling,which serve as physical qubits to support quantum channels.(b) Schematic illustration of teleporting the Werner state.The black particles (1,2) are physical qubits used to prepare the Werner state.The physical qubits of quantum channels are supported by two pairs of the entangled spins(3,5) and (4,6) in two same SGNRs,respectively.

其中σL(R)表示作用在左(右)锯齿端有效自旋粒子上的泡利算符,它的3 个分量分别由表示,Jt*2/U*表示这两个自旋粒子间的反铁磁耦合系数.这里t*≈1.29 e-L/1.86eV表示电子从一个锯齿端跳跃到另外一个锯齿端所需的能量,U*≈0.1U表示电子之间有效库仑排斥势.当系统处于绝对温度为T的热平衡态时,密度算符ρT为

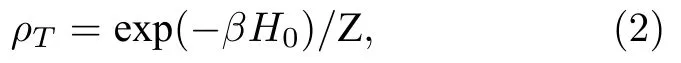
其中,β1/(kBT),kB为玻尔兹曼常数,ZTr[exp(-βH0)]为该系统的配分函数.在标准基组{|00〉,|01〉,|10〉,|11〉}下,(2)式可以表示为

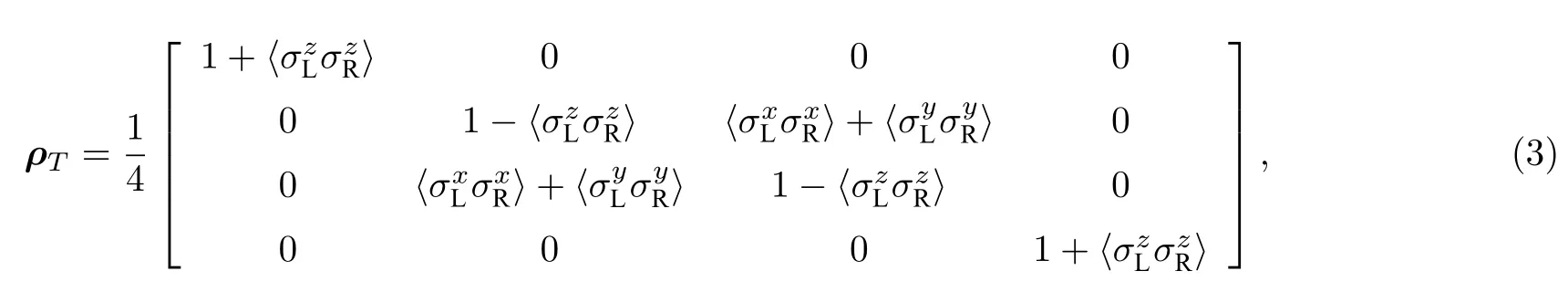
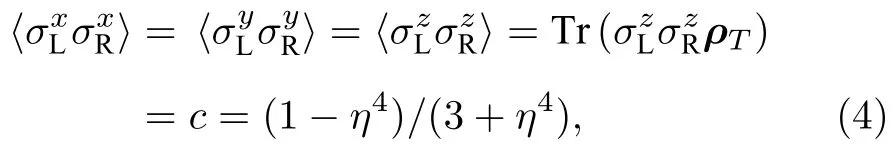
这里η是与自旋关联函数相关的参数,表达式为

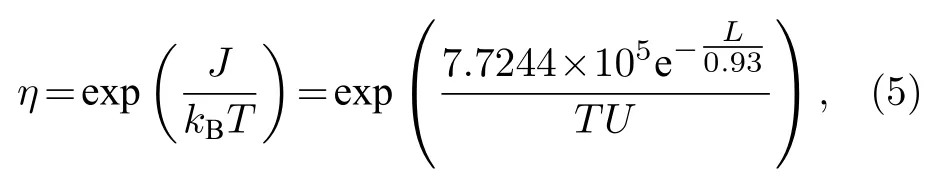
其中U表示电子间的库仑排斥势.于是,(3)式用自旋关联函数c可简化为

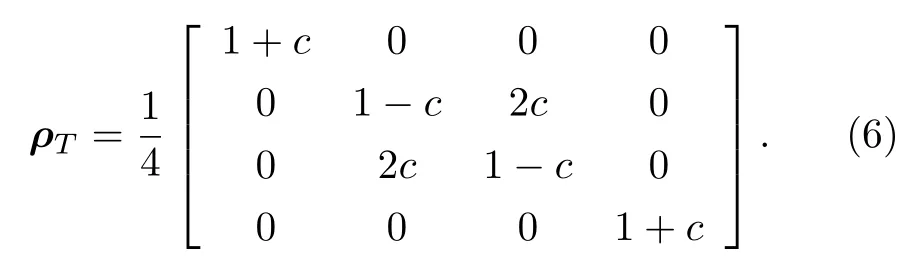
利用共生纠缠度Concurrence 可以对任意一个两体量子态ρ中的量子纠缠进行度量,其定义为[45]

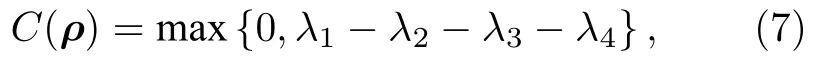
其中λk(k=1,2,3,4)是算符Rρ(σy ⊗σy)×ρ*(σy ⊗σy)本征值的方根,且满足λ1≥λ2≥λ3≥λ4,ρ*是ρ的复共轭.通过计算,得到热平衡态ρT的纠缠度为

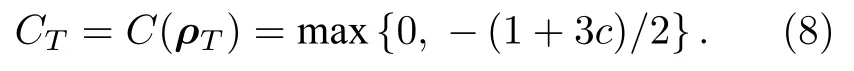
由于SGNR 两锯齿端上的自旋粒子间呈反铁磁耦合,所以自旋关联函数满足-1 ≤c≤0.根据(8)式可得,当-1 ≤c＜-1/3 时,一定有CT0 .因此,对于给定的排斥势U,只要外界温度不高于临界值

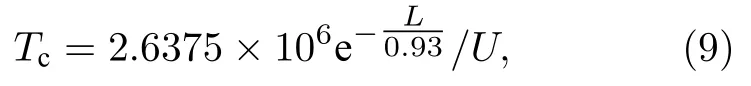
那么SGNR 两锯齿端上的自旋粒子间就一定存在量子纠缠CT.例如,对于宽度W=3 长度L=10 的SGNR,当温度T5 K,U3 eV 时,将(4)式和(5)式代入(8)式计算可得两自旋粒子间的纠缠度为CT≈0.9293 .因此可以利用该纠缠粒子对作为量子通道去实现量子态的隐形传输.在后续的讨论中固定选择宽度W=3 长度L=10 的两条SGNR 来构建量子通道.以Werner 态作为输入态来考察该量子通道的性能.Werner 态的一般形式为[46]ρin(1-b)I+b|Ψ-〉〈Ψ-|,其中|Ψ-〉(|01〉-|10〉)/b∈[0,1].在标准基组{|00〉,|01〉,|10〉,|11〉}下,Werner 态可以表示为

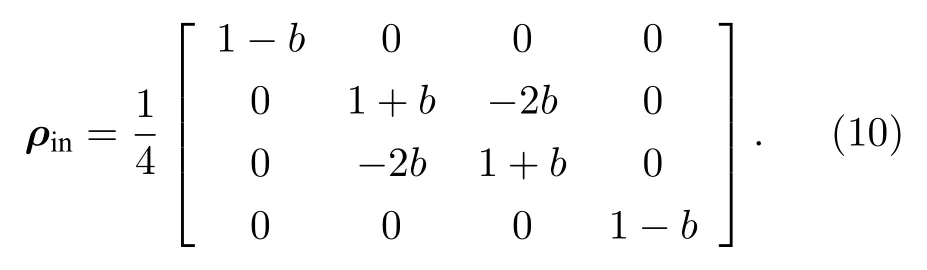
Werner 态的传输原理如图1(b)所示.假设Alice 要将一个未知的Werner 态发送给Bob,首先Alice 对A1和A2处的量子比特(1,3)和(2,4)进行联合贝尔基测量,结果将等概率地得到表1中16 个态中的一个.标准的贝尔基为E0|Ψ-〉〈Ψ-|,E1|Φ-〉〈Φ-|,E2|Φ+〉〈Φ+|,E3|Ψ+〉〈Ψ+|,其中,|Ψ±〉(|01〉±|10〉)/,|Φ±〉(|00〉±|11〉)/然后,Alice 将测量结果通过经典通道(如打电话、发邮件等方式)告诉Bob.最后,Bob根据Alice 的测量结果分别对B1和B2处的量子比特(5,6)进行相应的幺正操作(见表1),如I|0〉〈0|+|1〉〈1|,σx|0〉〈1|+|1〉〈0|,σyi|1〉〈0|-i|0〉〈1|,σz|0〉〈0|-|1〉〈1|,就能复原Werner 态.从整体效果来看,Werner 态会在量子比特1和2 上消失,最后在量子比特5和6 上出现.以上就是实现两体量子态隐形传输的基本方案,而在实际操作过程中由于环境的影响经常导致量子退相干现象的发生,这会对量子通道带来极大的影响.常见的退相干环境下的量子通道有振幅阻尼通道,退相位通道和退极化通道[47].本文主要考察退相位环境对SGNR 量子通道的影响.

表1 Alice 执行联合贝尔基测量所得的16 种可能结果与对应每种测量结果Bob 为复原Werner态所执行的幺正操作Table 1.Sixteen possible results of joint Bell-state measurements performed by Alice and the unitary operations performed by Bob according to each measurement result for restoring the Werner state.

3 结果与讨论

假设SGNR 锯齿端上的两自旋粒子各自分别与退相位环境作用.在这样的一个集体退相位环境下,量子态ρT将演化为

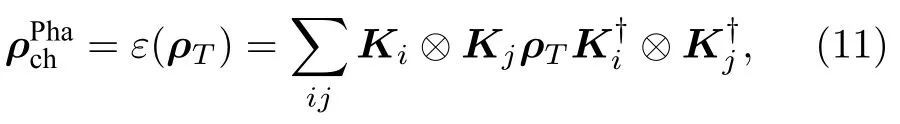
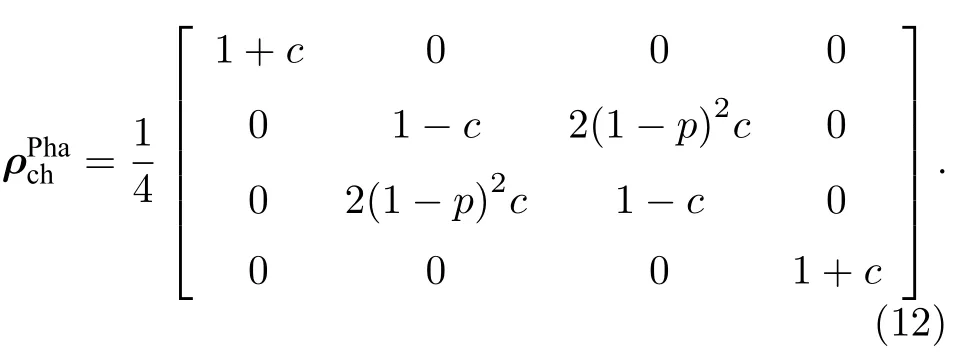
在退相位量子通道下,最终的输出态为[48]

其中,σ0I,σ1σx,σ2σy,σ3σz,E0|Ψ-〉〈Ψ-|,E1|Φ-〉〈Φ-|,E2|Φ+〉〈Φ+|,E3|Ψ+〉〈Ψ+|,|Ψ±〉(|01〉±|10〉)/,|Φ±〉(|00〉±|11〉)/在标准基组{|00〉,|01〉,|10〉,|11〉}下,(13)式可以进一步表示为

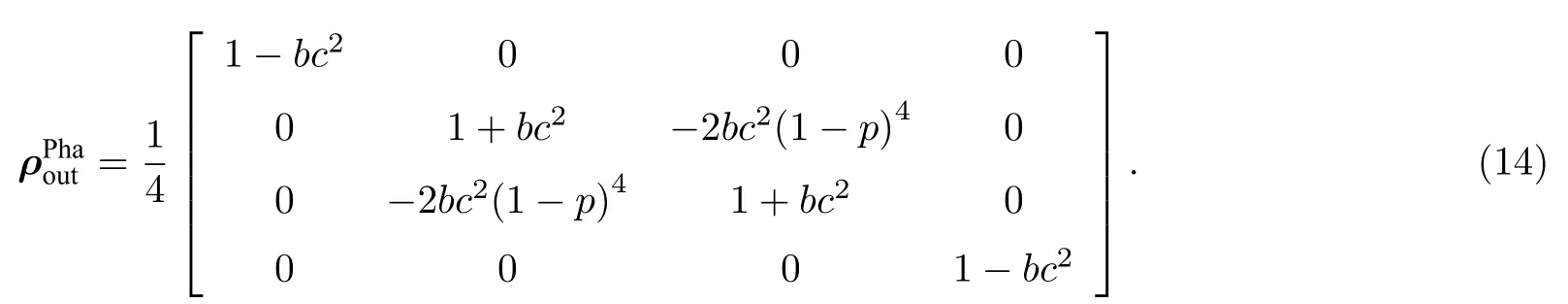
为了检验输出态的品质,需要计算保真度,其定义为[49]

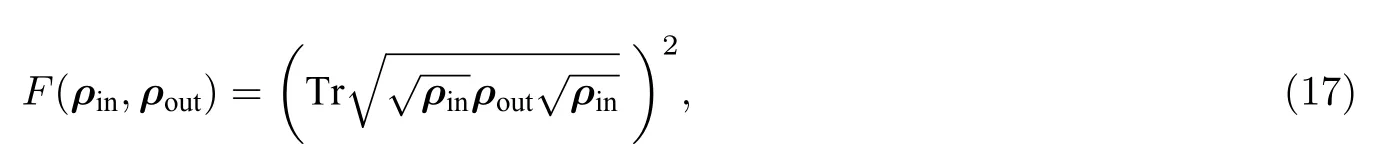
其中ρin和ρout分别表示输入态和输出态的密度矩阵.将(10)式和(14)式代入(17)式,最终计算得到下面通过数值计算来具体讨论退相位环境对SGNR 量子通道的影响.图2 给出的是退相位环境下通道态的纠缠度随温度T和出错概率p的变化.从可以看出,对于给定的库仑排斥势U,在低温且p比较小(即演化时间比较短)的条件下,通道态的纠缠度几乎趋近于最大值1;当温度T升高时,快速衰减,最终当温度达到某一确定值Tc时衰减为零;随着p的增大,不断衰减,最终在p=1 处衰减为零;通过比较图2(a)—图2(d)发现,对于给定的p,纠缠消失的临界温度Tc会随着U的增大而减小;当p=0 时,Tc的变化由(9)式决定.为了进一步考察U对量子通道的影响,计算了随U和p的变化,结果如图3 所示.当T=0 K 时,如图3(a)所示,随着p逐渐衰减,但其完全不受U的影响.通过计算绝对零度下的自旋关联函数,得到c-1,于是由(15)式可得(1-p)2,这就解释了图3(a)的结果.当T=5 K 时,从图3(b)可以看出,随着U的增大而减弱.当温度进一步升高时,通过与图3(c)和图3(d)的比较发现:温度越高,随U的衰减就越剧烈.这是因为当T和U增大时,由(5)式可知η在不断减小,于是由(4)式可知自旋关联函数c在不断增大.根据(15)式,对于给定的p,是关于c的单调递减函数,因此高温和强库仑排斥势对有着非常强的抑制作用.这也就意味着,在实际量子通信过程中,要尽量降低温度或者减弱库仑排斥势,这样才能使量子通道处在比较理想的状态.

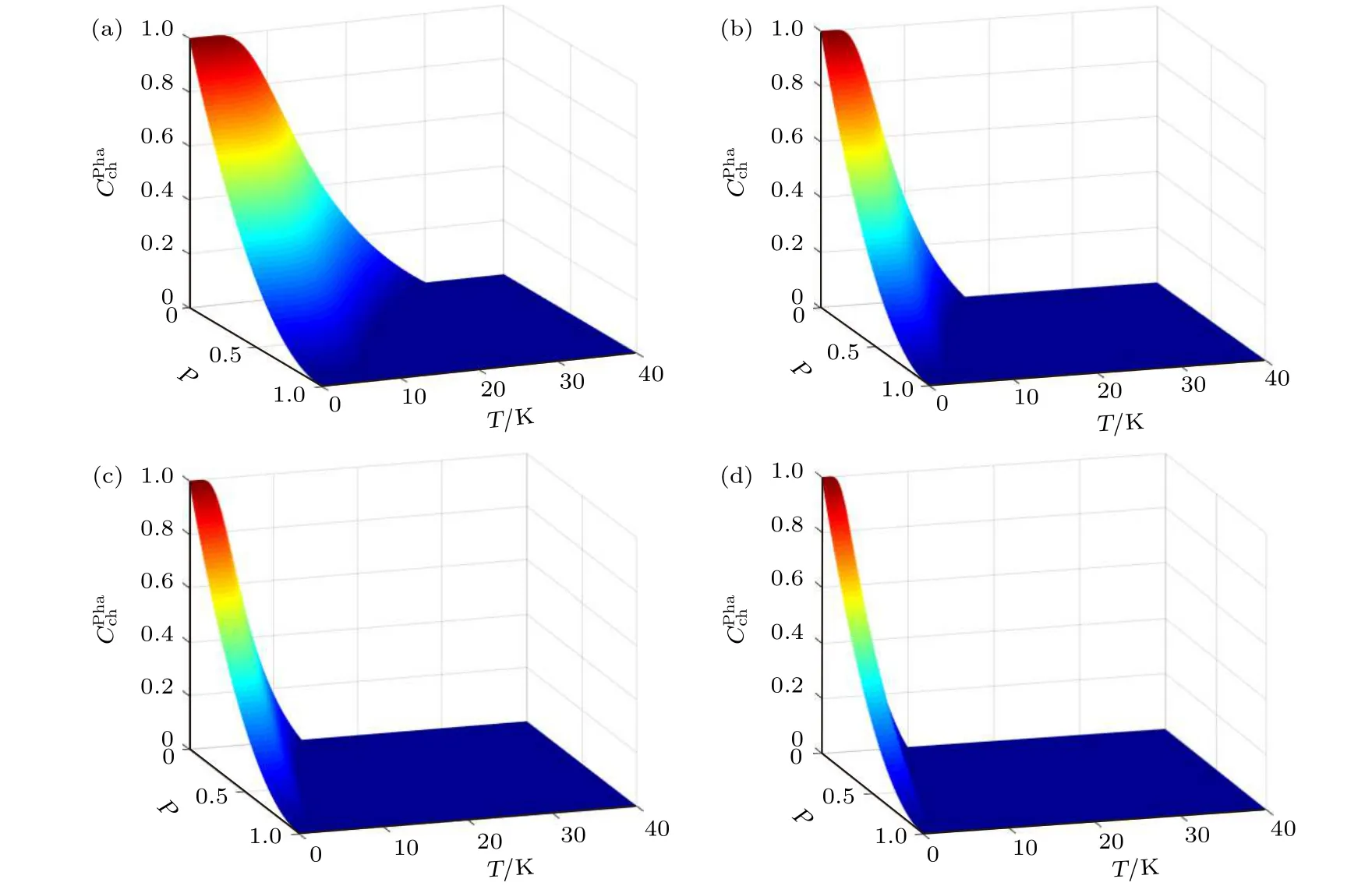
图2 退相位环境下通道态 的纠缠度 随温度T和出错概率p 的变化 (a) U=2.0 eV;(b) U=3.5 eV;(c) U=4.5 eV;(d) U=6.0 eVFig.2.Concurrence for the channel state in the dephasing environment as a function of temperature T and probability p:(a) U=2.0 eV;(b) U=3.5 eV;(c) U=4.5 eV;(d) U=6.0 eV.

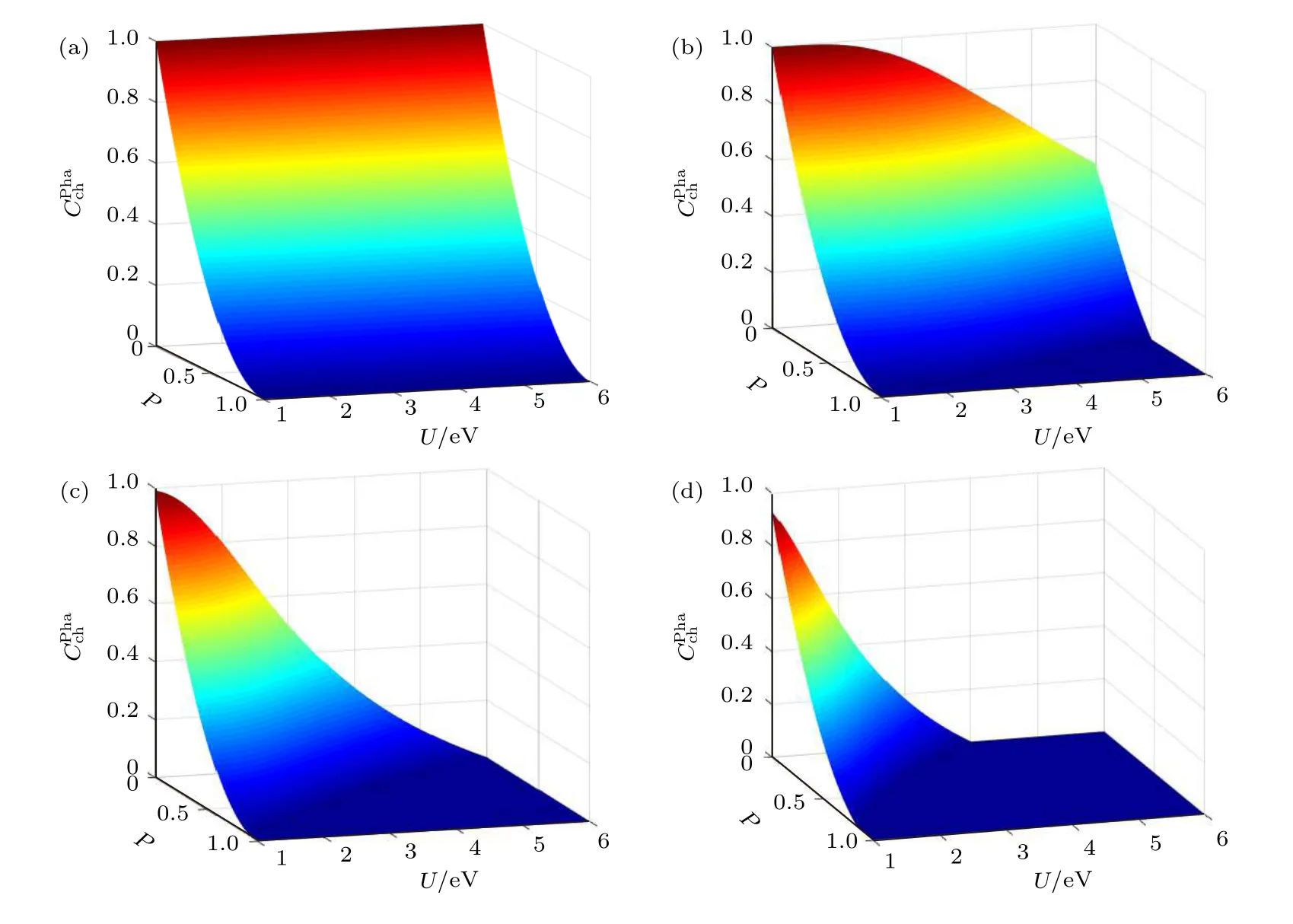
图3 退相位环境下通道态 的纠缠度 随库仑排斥势U和出错概率p 的变化 (a) T=0 K,(b) T=5 K,(c) T=10 K,(d) T=15 KFig.3.Concurrence for the channel state in the dephasing environment as a function of Coulomb repulsion U and probability p:(a) T=0 K;(b) T=5 K;(c) T=10 K;(d) T=15 K.

在退相位环境下Werner 态经量子和经典通道的传输,最终得到的输出态的纠缠度随参数b和出错概率p的变化如图4 所示.对于Werner态,当 0≤b≤1/3 时,结合(7)式与(10)式可得C(ρin)0,而当 1/3＜b≤1时,C(ρin)(3b-1)/2 .显然,输入态的纠缠度是关于b的单调递增函数.从图4(a)可以看出,当T=5 K,U=3.5 eV 时,随着b的增大而增大,随着p的增大而不断衰减;只有当输入态的纠缠比较鲁棒且演化时间比较短的情况下才有较为显著的纠缠输出.当T=5 K,U=6.0 eV 时,如图4(b)所示,被进一步削弱.当T=10 K,U=3.5 eV 时,只有在b=1 且p=0 附近才有微弱的纠缠输出,见图4(c).当T=10 K,U=6.0 eV 时,如图4(d)所示,输出纠缠0,即在此条件下无法完成纠缠态的传输,原因是此时量子通道中已经没了纠缠资源.

图4 退相位环境下输出态 的纠缠度 随参数b和出错概率p 的变化 (a) T=5 K,U=3.5 eV;(b) T=5 K,U=6.0 eV;(c) T=10 K,U=3.5 eV;(d) T=10 K,U=6.0 eVFig.4.Concurrence for the output state under the dephasing channel as a function of parameter b and probability p:(a) T=5 K and U=3.5 eV;(b) T=5 K and U=6.0 eV;(c) T=10 K and U=3.5 eV;(d) T=10 K and U=6.0 eV.

图5 退相位环境下输出态 的保真度 F(ρin,) 随参数b和出错概率p 的变化 (a) T=5 K,U=3.5 eV;(b) T=5 K,U=6.0 eV;(c) T=10 K,U=3.5 eV;(d) T=10 K,U=6.0 eV.Fig.5.Fidelity F(ρin,)for the output state under the dephasing channel as a function of parameter b and probability p:(a) T=5 K and U=3.5 eV;(b) T=5 K and U=6.0 eV;(c) T=10 K and U=3.5 eV;(d) T=10 K and U=6.0 eV.

为了更加客观地反映SGNR 量子通道的传输质量,计算了在此通道下传输一个任意Werner 态的平均保真度

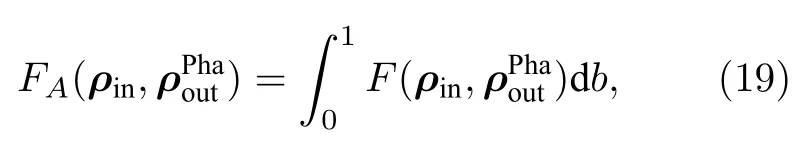
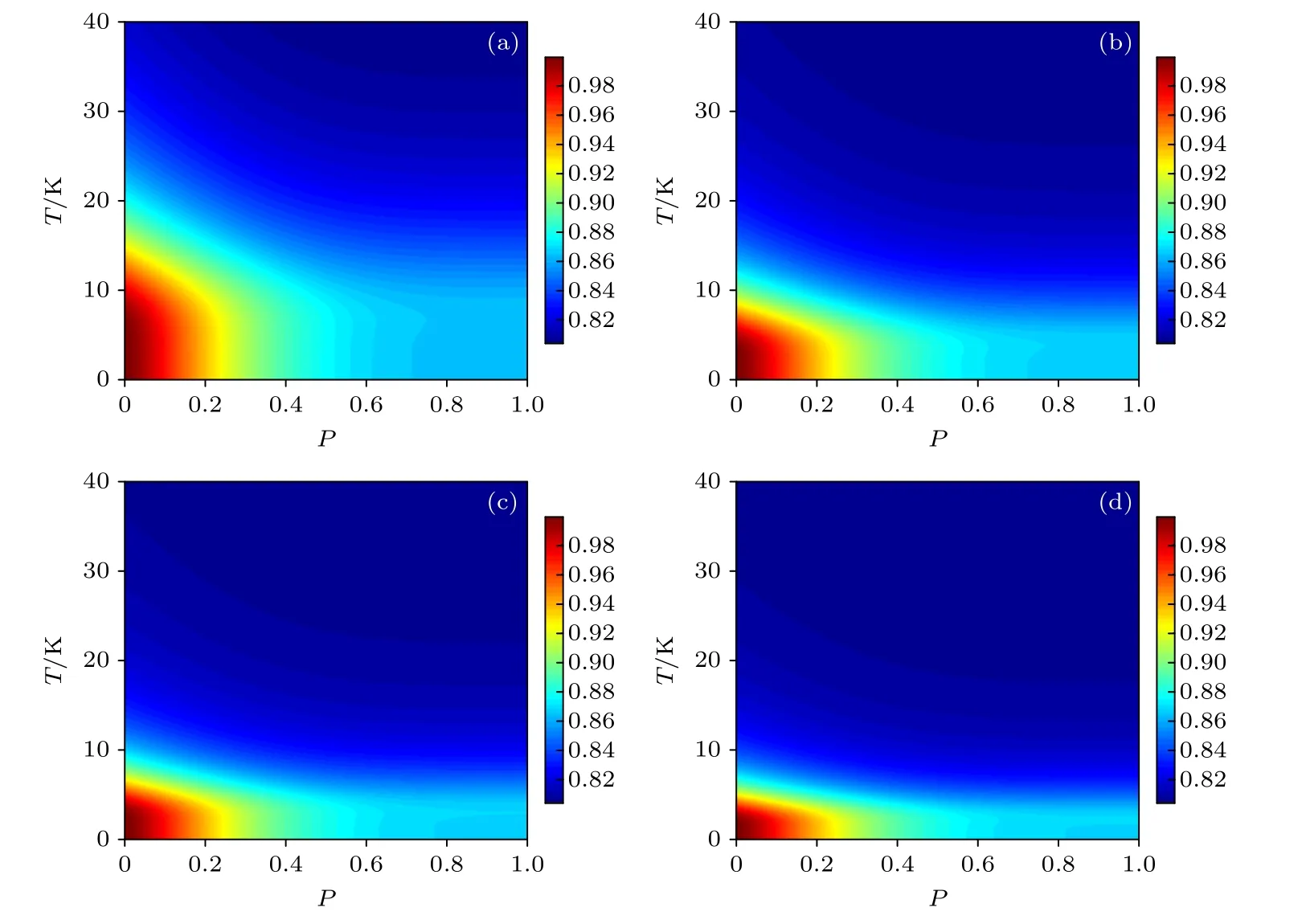
图6 退相位环境下输出态 的平均保真度 FA(ρin,) 随出错概率p和温度T 的变化 (a) U=2.0 eV;(b) U=3.5 eV;(c) U=4.5 eV;(d) U=6.0 eV.Fig.6.Average fidelity FA(ρin,) of the output state under the dephasing channel as a function of probability p and temperature T:(a) U=2.0 eV;(b) U=3.5 eV;(c) U=4.5 eV;(d) U=6.0 eV.

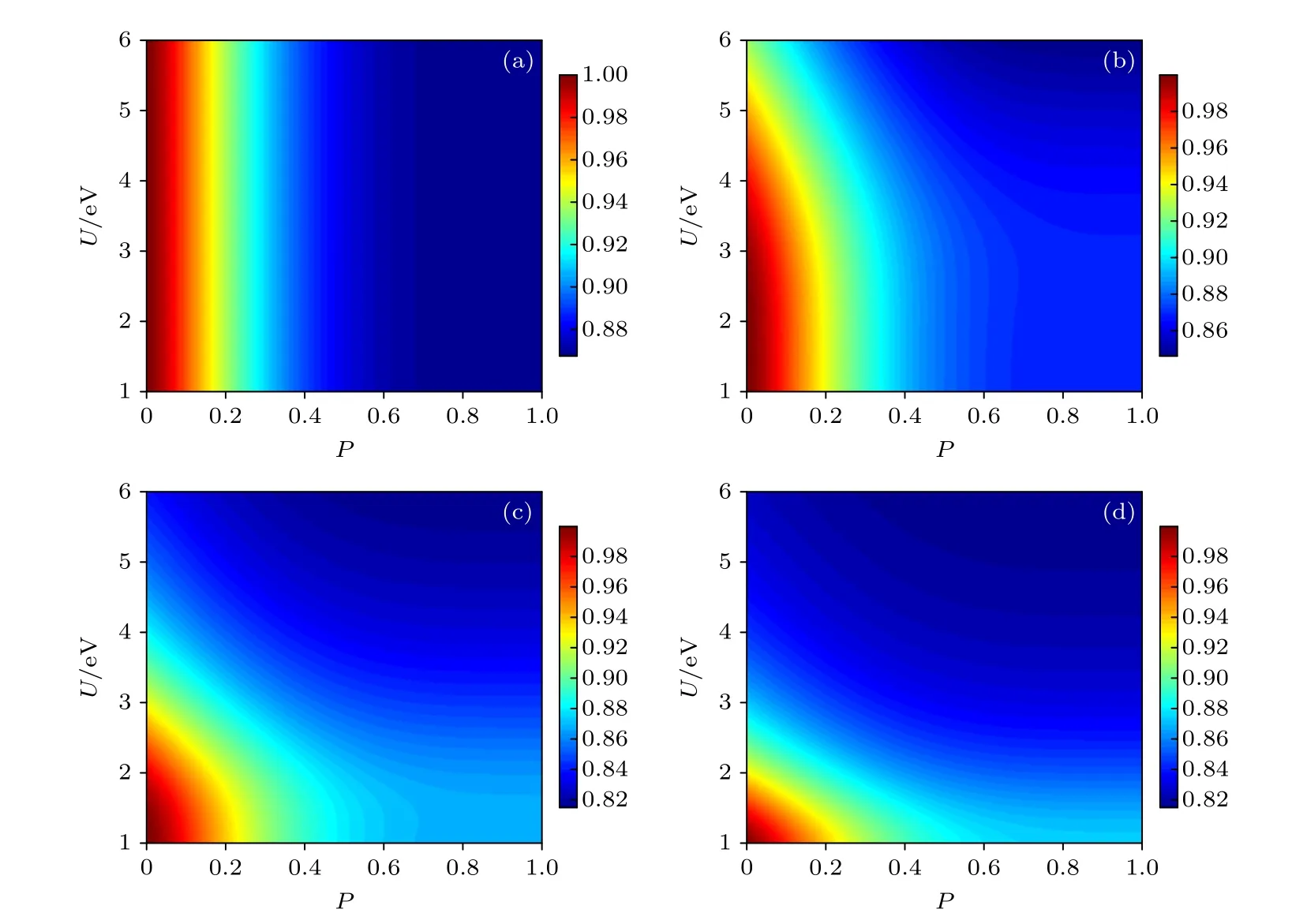
图7 退相位环境下输出态 的平均保真度 FA(ρin,) 随出错概率p和库仑排斥势U 的变化 (a) T=0 K;(b) T=5 K;(c) T=10 K;(d) T=15 KFig.7.Average fidelity FA(ρin,) of the output state under the dephasing channel as a function of probability p and Coulomb repulsion U:(a) T=0 K;(b) T=5 K;(c) T=10 K;(d) T=15 K,respectively.

4 结论

本文研究了退相位环境下Werner 态在SGNR量子通道中的隐形传输.结果表明,输出态的纠缠度和保真度对量子通道中的纠缠资源以及输入态的纠缠度有很强的依赖性.对于给定的输入态,量子通道中的纠缠越大,输出态的品质就越高;对于给定的量子通道,输出态的纠缠度总是随着输入态纠缠度的增大而增大,而相应的保真度却总是随着输入态纠缠度的增大而减小.由于受退相位环境的影响,量子通道中的纠缠资源会随着时间演化而不断损耗,高温和强库仑排斥势会加剧这种损耗,从而导致输出态的品质下降.但是当温度小于40 K,且电子间的库仑排斥势小于6 eV 时,输出态的平均保真度总可以达到80%以上,且平均保真度在退相位环境中的衰减并不明显.因此,SGNR 量子通道在退相位环境下有非常好的鲁棒性.特别是对于低温和微弱的排斥势,输出态的平均保真度几乎接近最大值1.以上结果充分说明石墨烯材料在量子信息领域中具有潜在的应用价值.