熵不确定度关系综述*

李丽娟 明飞 宋学科 叶柳 王栋†

1) (安徽大学物理与光电工程学院，合肥 230601)

不确定关系是量子力学的基本特征之一,随着量子信息理论的蓬勃发展,不确定关系更是在其中发挥着重要的作用.特别是将熵引入来描述不确定关系之后,不确定关系在量子信息技术中涌现出多种应用.众所周知,熵不确定度关系已成为几乎所有量子密码协议安全分析的核心要素.这篇综述主要回顾不确定关系的发展历史和最新研究进展,从Heisenberg 提出不相容测量其结果是不能被预测伊始,许多学者在该观点的启发下,做了进一步的相关扩展研究,将可观测物体与环境之间的量子关联结合起来,对不确定关系进行各种推广从而得到更普适的数学表达式.除此以外,本文还重点介绍了量子存储下的熵不确定度关系及其发展,也介绍了在某些物理系统中对应的动力学特性.最后讨论了熵不确定度关系在量子信息领域的各种应用,从随机数到波粒二象性再到量子密钥分发.

1 引言

量子力学颠覆了我们一直以来用经典力学的方式来研究世界运行规律的传统观念,许多无法用经典力学理论来解释的微观现象,量子力学都可以解释.在量子力学领域,不确定关系是一个极为重要的概念,也被称作测不准关系,它实质上反映的是微观粒子运动的基本规律,这也是量子力学区别于经典力学的判据之一.1927 年,Heisenberg[1]通过对假想实验的分析首次提出不确定关系(示意图参照图1),该不确定关系展示了人们无法同时准确预测一对非对易观测量的测量结果,也就是说,对粒子动量预测的结果准确性越高,那么对其位置预测的准确性就越低,反之亦然.随后,这个关系式由Kennard[2]给出了严格证明.随着深入研究,人们发现,不确定关系不仅适用于位置和动量这对非对易物理量,对于其他成对的非对易可观测量同样适用,比如谐振子的相位与激发数、粒子的角度与轨道角动量等.据此,关于任意两个可观测量,Robertson[3]提出了更为普适的不确定度不等式.值得注意的是,这个公式虽然普适,但也不是量化不确定性的最佳不等式,它亦有不足之处,这点本文将在第2 节中给出具体分析.

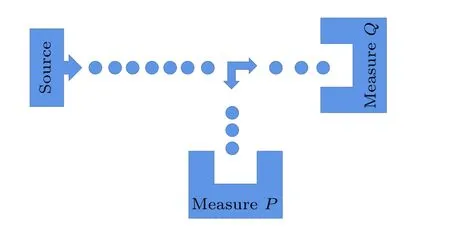
图1 每个从粒子源发出的粒子都是用P 或Q 来测量的,测量的选择是随机的.不确定关系指出我们不能预测P和Q 的测量结果Fig.1.Each particle emitted from the particle source is measured by P or Q,and the choice of measurement is random.The uncertainty relation indicates that we cannot predict the outcomes of both P and Q.

随着量子信息理论的不断发展,Deutsch[4]指出标准差用来量化不确定度有它自身的局限性,同时学者们发现标准差并不是量化不确定度的唯一方式,所以也逐渐衍生出许多其他方式来量化不确定度.其中,Everett[5]和Hirschman[6]首次提出关于位置和动量的熵不确定度关系,这也是第一个熵不确定度关系.随后,这个不确定关系被推广到任意两个非对易的可观测量.由于Robertson 提出的不等式下界是依赖于系统的态,为了克服这一弊端,Deutsch[4]利用信息熵构造了一个全新的熵不确定度不等式.之后在Kraus[7]推测的启发下,Maassen和Uffink[8]延续Deutsch 的结论进而提出了一个著名的熵不确定度关系式.除上述方式之外,本文第2 节将回顾多种形式的不确定关系.

通常情况下,人们可用猜测游戏来演示不确定关系的物理意义.在猜测游戏中(如图2 所示),假设有两位观察者Alice和Bob,现在Bob 准备了一个任意的态ρA并且将它发送给了Alice,Alice在收到这个态之后,随机在两个(或多个)测量选择中选定某一个作用在态ρA上,并记录下测量结果,随后Alice 告诉Bob 她的测量选择,Bob 的任务就是猜出Alice 的测量结果.不确定性原理告诉我们,如果Alice 做了两个不相容的测量,那么Bob 就无法准确地猜测出两次测量的结果,这也正好对应了制备不确定性的概念.而熵不确定度关系,比如Maassen-Uffink 关系式可以被认为是最佳猜测概率的基本约束.这个猜测游戏引发学者继续思考:在刚提及的游戏中,Bob 只能通过经典信息来获得关于被测粒子制备的相关信息,若让Bob 除经典信息外还能获取相关量子信息,那么能否提高Bob 对Alice 的测量结果的猜测概率呢？具体来说也就是如果Bob 准备的是一个双粒子系统,且这两个粒子之间是相互关联的,随后Bob 只发送了其中一个粒子给Alice,留下另一个粒子作为量子存储,那么在这种情况下,Bob 就可以通过两粒子之间的关联获取量子信息,考虑到这些,Berta 等[9]以及Renes和Boileau[10]顺着这个思路完成了相关研究,并提出了一种新的熵不确定度关系,被称为量子存储下的熵不确定度关系,随后也有许多工作在该主题下展开,比如三体系统的熵不确定度关系,还有各种模型下熵不确定度动力学等,这些工作进展都将在本文的第3 节中一一展示.

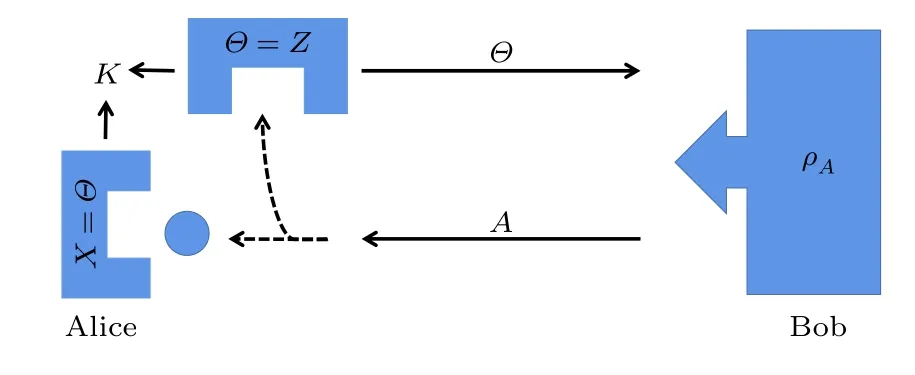
图2 玩家Alice和Bob 的猜测游戏.首先,Bob 准备ρA并把A 发送给Alice.然后,Alice 以相等的概率进行 Q或R测量,并将测量选项存储在Θ 中.第三,Alice 得出测量结果并将其存储在K,且向Bob 透露测量选择Θ.Bob 的任务是猜测K(给定Θ)Fig.2.A guessing game between players Alice and Bob.First,Bob prepares ρA and sends A to Alice.Then,Alice performs measurement Qor R with equal probability on A,and stores the measurement options in Θ.Third,Alice stores the measurement result in the K bit and tells Bob about her option Θ.Bob’s task is to guess K (given Θ).

除了在理论上对不确定关系进行不断地探索之外,量子信息理论的蓬勃发展也为不确定度关系打开了应用的大门.目前,不确定度关系广泛应用于包括纠缠目击、量子隐形传态、量子密码学、量子密钥分发、随机数等量子信息研究领域,相关应用将会在第4 节进行详细的讨论.

2 不同种类的不确定关系

不确定关系最开始是基于动量和位置提出的,随着量子信息理论的兴起和发展,众多学者在研究不确定关系的过程中引入标准差、熵等概念,逐渐形成了不同种类的不确定关系分支,本节主要考虑单个系统A的不确定关系,介绍几种不同形式的不确定关系.

2.1 基于标准差的不确定关系

首先,Heisenberg[1]提出了著名的不确定性关系,并由Kennard 进行了严格的证明,它可以表示为

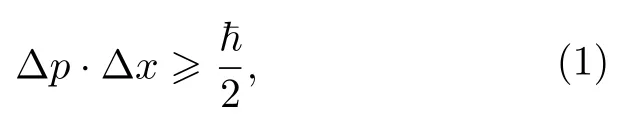
这里的 Δx和 Δp分别代表位置和动量的标准差ℏ 是普朗克常数.该不确定关系指出人们无法同时确定地获得某个粒子的位置和动量的精确测量结果.在此基础上,对于任意两个非对易的可观测量Q和R,Robertson[3]推广得到了一个新的不等式:

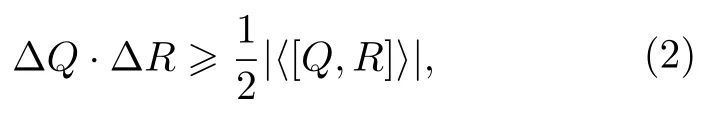
这里的[Q,R]QR-RQ,〈τ〉〈ψ|τ|ψ〉是可观测量τ在量子态|ψ〉下的期望值.正如引言所说,(2)式并不是完美的,它的缺点是当系统准备的态是选取的两个可观测量的本征态时,通过计算可知,Robertson 不等式所展现出的下界(不等式的右侧)就会变为零,此时结果显得过于平庸.也就是说这个不等式的下界依赖于系统的态.接着Schrödinger[11]通过附加一个反对易子项强化(2)式得出:

然而,(2)式和(3)式的下界是与状态相关的.如果系统由Q或R中的某一个本征态制备,很容易算出来,即(2)式和(3)式的下界为零,这意味着在这种情况下,用标准差来测量不确定性将变得没有意义.随后Maccone和Pati[12]为了消除了这个缺点提出了一个新的不确定关系:

这里的B1±i|〈[Q,R]〉|+|〈ψ|Q±iR|ψ⊥〉|2,B2态|ψ⊥〉正交于|ψ〉.(4)式表示的不确定关系已经在实验[13-15]上得到了验证.

2.2 基于熵的不确定关系

从技术上讲,除了上面提到的偏差以外还有另一种有效而直接的方法来描述不确定性关系,即熵.Everett[5]和Hirschman[6]首次引入熵来描述测不准原理.随后,Białynicki-Birula和Mycielski[16]严格证明了关于位置与动量的微分熵不确定度关系:

其中h表示的是微分熵,考虑一个由概率密度Γ(q)控制的随机变量Q,微分熵可以表示为

假设这个量属于高斯概率分布,则满足

将(7)式代入(6)式来计算高斯分布的熵更直观,代入得到:

又由于高斯概率分布使熵最大化,所以对于一个一般分布的随机变量,下面的不等式始终成立:

现在考虑粒子平移自由度的任意量子态,它分别产生位置和动量的随机变量Q和P,然后将得到的结果不等式代入到(5)式得出

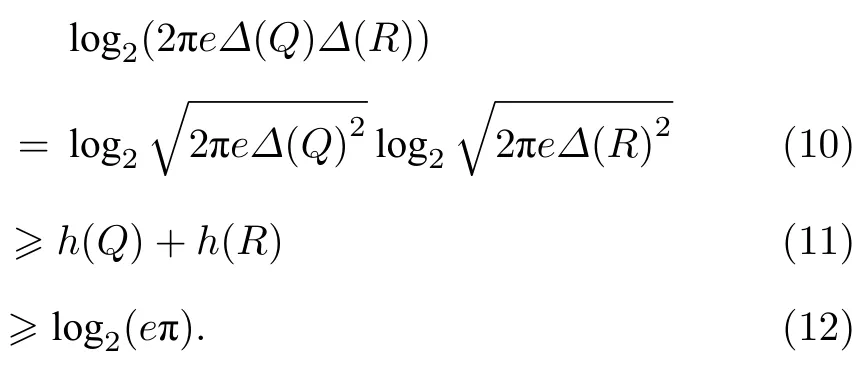
最后,结合(10)式和(11)式很容易推断出之前关于位置与动量的结果 Δx·Δp≥ℏ/2 .

众所周知,香农熵[17]在信息论中起着基础而又关键的作用,在经典物理学领域量化了给定系统状态下的信息量.通过引入香农熵,Deutsch[4]提出了一个不确定关系,写成

随后,基于Deutsch 的开创性工作,Maassen和Uffink[8]遵循Kraus 的猜想对(13)式进行了优化,对任意的态ρA,

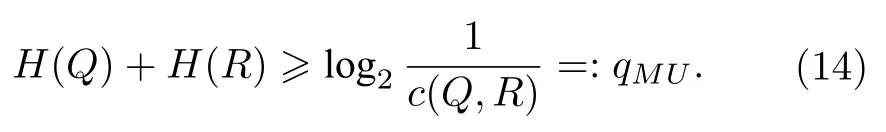
注意(13)式和(14)式中的下界都是和初态无关的,这一点和Robertson 提出的下界形成了对比.Korzekwa 及其团队[18]表示,通过考虑总的不确定性,单比特系统的Maassen-Uffink 不等式可以改进为

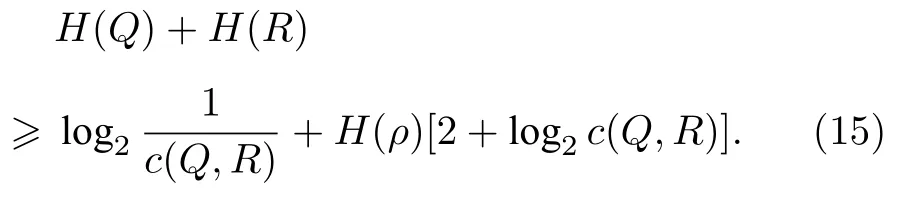
此外,从香农熵出发,Rényi[19]提出一个相对更普遍的熵版本,可以为具有高或低信息量的事件提供更大的权重.由于其固有的数学性质,这些不同类型的熵可以很好地应用于量子密码学和信息论.一般来说,x阶的Rényi 熵定义为

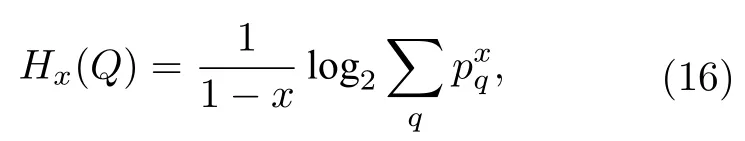
x的范围是[0,∞] .当x1 时,Rényi 熵就会恢复到Shannon 熵,Shannon 熵可以说是Rényi 熵的一种特殊形式.Maassen和Uffink[8]还指出,从Rényi 熵的角度出发(14)式会变得更普适,对任意的,有以下关系:

当xy1时,(17)式和(14)式一致,当x→∞,y→时,可以得到另一个关于(17)式用最小熵和最大熵来描述的特殊例子:

由于最小熵表征了正确猜测结果Q的概率,因此这种类型不确定关系在量子密码学和量子信息论中应用最为广泛.

除上面说的三种熵不确定度关系外,也有学者推导出了时间-能量熵不确定度关系[20],比如Rastegin[21]通过Pegg[22]的方法推导出了能量-时间的熵不确定度关系.

2.3 Majorization 不确定关系

另外一种获得与熵直接相关的不确定关系的方法就是Majorization 方法,代替之前的概率之和,该方法采用的是概率的乘积.这个想法是由Partovi[23]首次提出,然后由Friedland 小组[24]和Puchała 小组[25]进一步推广和发展.现有两个半正定算子值(positive operator-valued measures,POVM) X{Xx}x和 Z{Zz}z,用这两个测量对系统ρA进行测量,根据玻恩定则可以得到概率分布分别为PX(x)Tr(ρAXx)和PZ(z)Tr(ρAZz) .可以用和来表示相应的重新排序的向量,方便概率按从大到小的顺序排列.

对∀ρ∈S(H) 即希尔伯特空间都成立.这样的关系式给乘积分布如何展开设置了一个界,一个满足(19)式的概率分布µ可以这样来构造,考虑到(19)式中乘积分布的最大概率:

我们知道如果两个测量是不相容的,那么p1总是会远离1,因为不可能两个测量都有一个确定的结果.举例说明,回想一下Deutsch 的结果,可以得到

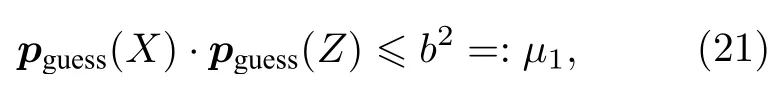
除此以外,Friedland 小组和Puchała 小组都提到了用一套有效的方法来构造一个向量序列形式为

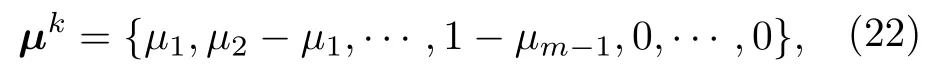
同时μk ≺μk-1满足(19)式并且带来了一个越来越紧致的不确定关系.μk的表达式是根据Majorization 问题给出的,并且会随着k的增加而变得越来越难.

这里要说明的是,Rényi 熵的熵不确定度关系是直接由Majorization 关系派生而来的,这是由于Rényi 熵是Schur 凹的,且具有可加性.这代表了

这里的V是一个根据µ规律分布的随机变量,与公式(7)中的Maassen-Uffink 关系相比,(23)式中的不确定关系具有不同性质,因为它给出了具有相同参数的Rényi的总和的下界.作为一个x→∞的特例,又恢复到了Deutsch 提出的熵不确定度关系:

第一行的不等式是通过以α为参数的Rényi 熵的单调性推出的,若α1,再根据(23)式,可以得到

这里的Hbin(Λ)-ΛlogΛ-(1-Λ)log(1-Λ) 指二元熵.

3 量子存储下的熵不确定度关系

3.1 背 景

在开始介绍量子存储下的熵不确定度关系之前,为了更好地理解接下来的内容,需要先引入几个概念及他们的数学表达式,首先von Neumann[26]为了描述量子体系将熵的概念推广到量子范畴,即冯诺依曼熵,它可以用来表征量子态的不确定度,计算方法如下:

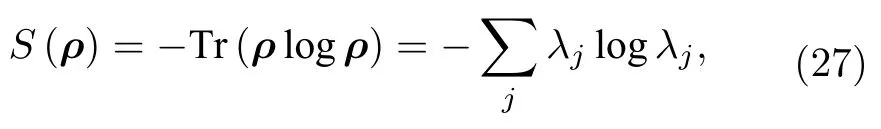
λj代表量子态ρ的本征值.对于一个双边量子态ρAB,量子联合熵、量子条件熵以及量子互信息可以表示为

接着可以利用下面的式子来计算经典关联C(B|A)和量子失谐D(B|A) :

目前为止,上面所展现出的不确定关系都是有限制的,他们都只允许观察者获得有限的经典信息,前面的猜测游戏中提出的问题,即如果Bob 除了经典信息之外还能根据两个关联的粒子获取相关的量子信息,是否可以提高Bob 对Alice 测量结果的概率呢？Renes和Boileau[10]在这个问题上做出了尝试并且得到了相关的结果,也为熵不确定度关系研究打开了一个新的局面,他们利用两个互补的测量基X和Z得到了如下的不等式:

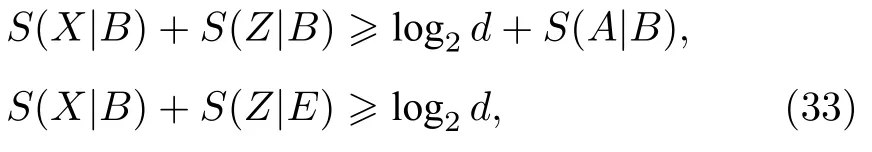
d代表A粒子维度,E代表窃听者Eve 的系统.

接着,Berta 等[9]在Renes和Boileau 的结论上做出了新的突破,将(33)式进一步推广到了任意两个可观测量,现在解释Berta 等提出的不确定游戏是如何实现的.与之前猜测游戏不同的是,这个游戏的规则是允许Bob 保留量子存储系统来帮助他猜测Alice 的测量结果,如图3 所示.两个游戏玩家必须事先知晓两个测量Q和R,Bob 先准备一个双粒子系统态ρAB,AB粒子相互纠缠,Bob将粒子B留下,将粒子A发送给Alice,Alice随机选择对粒子A进行测量,并且把自己的测量选择告诉Bob,Bob 的任务仍然是预测Alice 的测量结果,此时Bob 这里有和粒子A存在纠缠的量子存储粒子B,Bob 可以通过利用他所收到的经典信息来对粒子B进行测量.S(Q|B) 是用来衡量Bob 关于Alice 用可观测量Q的测量结果的不确定度,S(R|B)也是同样的意义.Berta 等[9]提出了量子存储支撑下的熵不确定度关系:

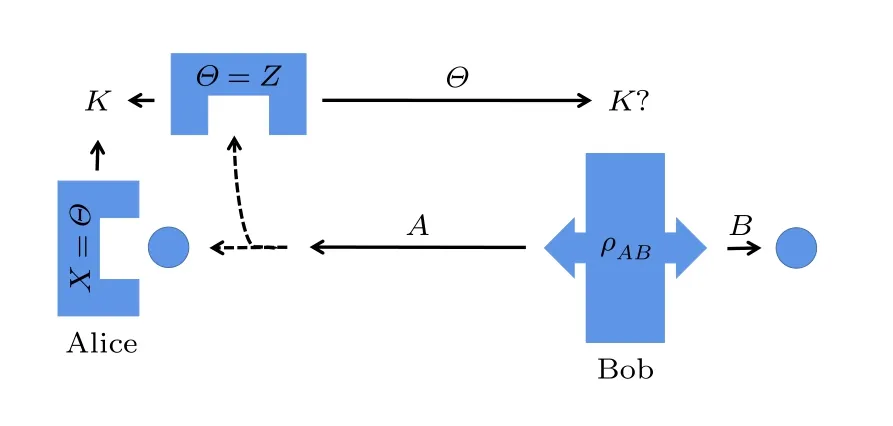
图3 量子存储下的不确定游戏.首先,Bob 准备态 ρAB,然后把子系统A 发送给Alice.第二,Alice 对A 进行 Q和R 测量,然后向Bob 告知测量选择Θ.Bob 的任务是正确猜测KFig.3.The guessing game with a quantum memory system.First,Bob prepares ρAB and sends A to Alice,Then,Alice performs measurement Qor R on A,and stores the measurement options in Θ.Third,Alice tells Bob about her option Θ.Bob’s task is to guess K correctly.

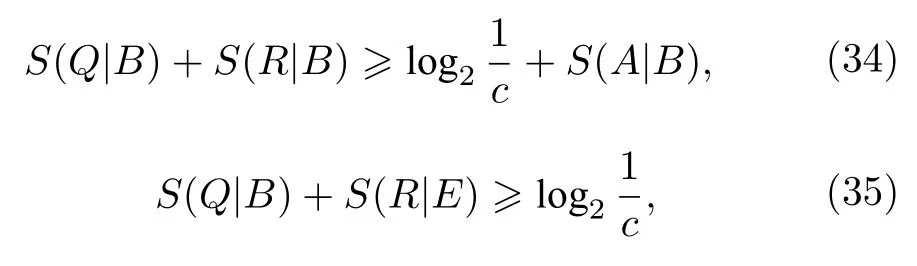
其中,S(A|B)S(ρAB)-S(ρB) 代表测量前的态ρAB的条件熵,S(Q|B)S(ρQB)-S(ρB) 代表的是经过Q测量过后的态ρQB的条件熵,可以通过如下的式子求出经过测量的态:

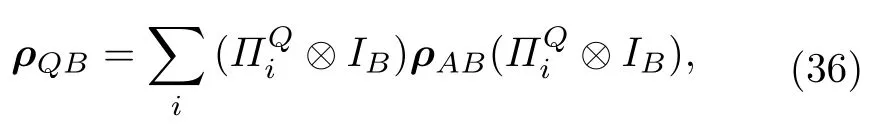
Berta 等的结果已在全光平台中得到验证[27-28],也有人提出了利用金刚石氮空位色心体系进行验证[29].除这些以外,量子存储下的熵不确定度关系在近些年也在不断发展、完善,这些进展都会在接下来的章节中介绍.

3.2 进 展

3.1 节主要介绍了量子存储下熵不确定度关系的背景起源,接下来展示的是近些年来量子存储下熵不确定度关系的发展方向及进程.

3.2.1 两粒子系统量子存储下的熵不确定度关系

首先在两粒子量子存储下熵不确定度关系方面,继Berta 之后,许多学者也在不断进行探索,他们发现考虑到粒子A,B间的量子关联,可以得到比(34)式更为优化的下界,Pati 等[30]证明了(34)式可以更加紧致:

其中δ1D(ρAB)-C(ρAB) ,C(ρAB) 是经典关联,D(ρAB) 是量子失谐[31],数学表达式如(31)式和(32)式.证明方程的关键是S(X|B)S(X)-I(ρXB)(X表示测量Q,R),I(ρXB)≤C(B|A)和H(Q)+H(R)≥qMU,这表明当量子失谐大于经典关联时,Pati 等提出的不确定度下界较(34)式的下界更为收紧.如果考虑到量子态ρAB的纯化|ψABC〉,量子失谐和经典关联之间的差异遵循单配性分配[32,33]:

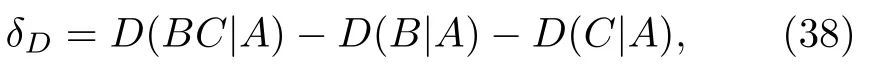
因此只有在量子态ρAB的纯化|ψABC〉违反单配性不等式D(BC|A)≥D(B|A)+D(C|A) 时,Berta 等的不确定度下界才会被提高.

同样的,(35)式下界也可以被优化为

其中,C(B|A)-D(BE′|A),D(BE′|A) 代表系统A和BE'之间的量子失谐,E'指代ABE的纯化系统,即ρABETrE′(|Ψ〉ABEE′〈Ψ|) .

回到(34)式的下界优化问题上,2014 年,Coles和Piani[34]在紧致界方面做出了突破,他们引入{cij}中第二大的参数c2先推导出了新的不确定度关系式:

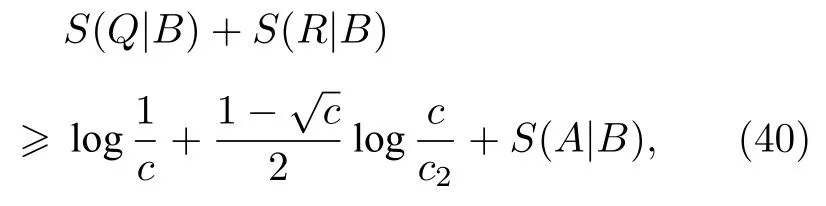
并进一步证明了下面紧致的不确定度关系下界:

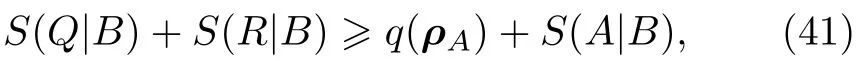
式中的q(ρA)max{q(ρA,Q,R),q(ρA,R,Q)},计算方式如下:

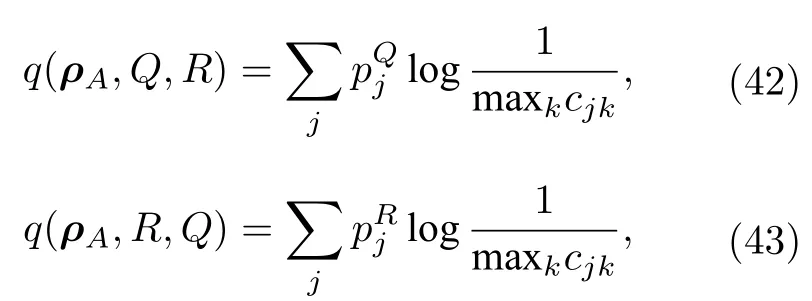
还可以在全套的ρA找出最小的q(ρA),也就是qminρAq(ρA),Coles和Piani 提出这种最小化可以通过以下步骤实现:

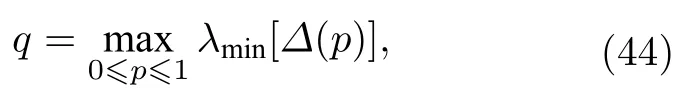
λmin[Δ(p)]表示矩阵varΔ(p)pΔQR+(1-p)ΔRQ的最小本征值,其中

同样,(40)式和(41)式的不确定下界可以通过在不等式右侧加上额外的一项 max{0,δ1}而变得更为紧致.

Adabi 等[35]以及Haseli和Ahmadi[36]从Holevo量和互信息方面出发,提出了如下表达式:

其中I(ρQB) 代表着Bob 对Alice 的测量Q可获取的信息量,I(ρRB)也是一样,因此当互信息I(ρAB)大于Bob 可获取的信息之和时,(46)式给出的下界将会比Berta 给出的下界更为优化,对于两粒子纯态,经计算可得δ1χ2,此时,(46)式给出的下界将会和(34)式和(37)式的下界保持一致,除此之外,Adabi 等[35]还讨论了对Werner 态,(46)式的下界将会和(37)式的下界重合,但是对于贝尔对角态和两量子比特X态,Adabi 的下界结果明显优于(34)式和(37)式的.

由Berta 等[9]提出的熵不确定度关系适用于两个可观测量的情况,实际上这个关系可以被推广到更一般情况,也就是多测量设置情况,沿着这个想法,不少学者也在这个方向上做出了突破[37],下面给大家展示一些代表性的相关工作,Berta 等提出的不确定游戏中是两测量(Q和R),那么多测量的情况会是怎么样？根据Liu 等[38]提出的新量子存储下熵不确定度关系,假设这两个测量被N个测量所代替,那么有:

此外,也可以利用其他方式来优化(49)式的下界,Dolatkhah 等[40]采用Adabi 等在这篇文章中一样的方法推导出

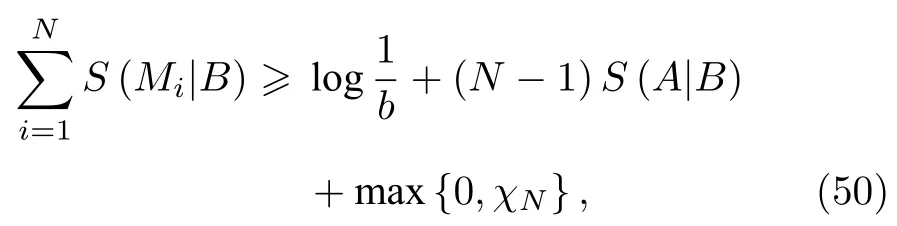
除此以外,利用Pati 等紧致下界的方法思路,也有学者推导出了在没有量子存储器的情况下多测量的熵不确定度关系[38]:

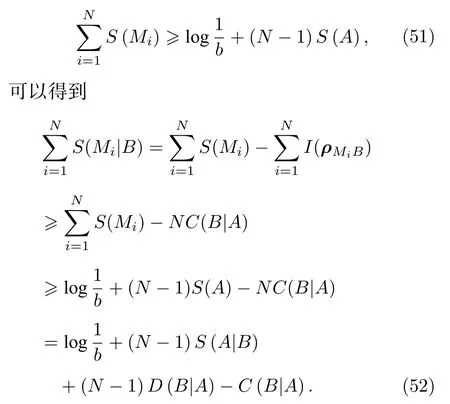
将(52)式进行整合简化,可以得到一个比Liu 等的下界((47)式)更为紧致的下界,表示如下:

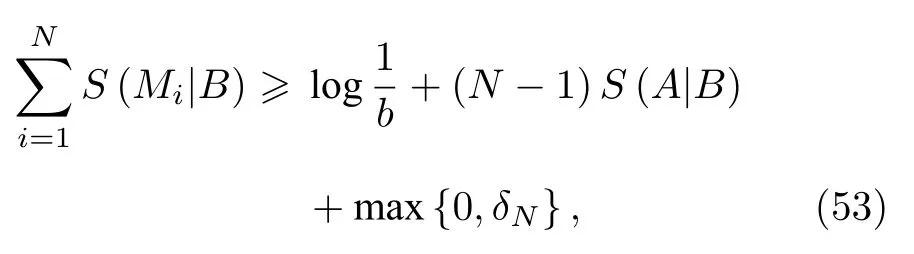
这里的δN(N -1)D(B|A)-C(B|A) .

Hu和Fan[41]从另外的角度来分析量子存储下的熵不确定度关系,他们从Berta 等提出的结论((34)式)出发,将不确定游戏推广到了这样情况,现有N个玩家共享量子态所有玩家都知道这个态的具体形式除了,玩家Alice,那么玩家B1B2···BN-1之间禁止交流,他们的任务就是预测出Alice 作用在粒子A上的测量结果,依赖于冯诺依曼熵的强次加性和条件熵的次加性[42],可以得到:

从(54)式联系到上面的游戏情况,可以这样理解,Alice 对粒子A的测量结果不能被其余玩家B1B2···BN-1同时准确预测,从这个角度分析得出的(54)式被认定为是不同种的不确定关系.

3.2.2 三粒子系统量子存储下的熵不确定度关系

2009 年Renes和Boileau[10]给出了三粒子系统中量子存储下熵不确定度关系的具体形式:

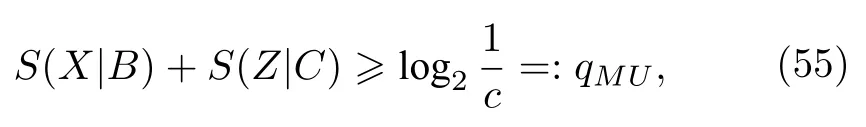
这里可以用单配性游戏来解释.如图4 所示,假设现在有一个输出三粒子系统态ρABC的发射源,现将子系统A,B和C分别发送给Alice,Bob和Charlie三人,接着,Alice 对系统A进行X或Z测量,如果选择X测量,将选择告诉Bob,Bob的任务就是以最小的不确定性猜出测量结果.同样,如果选择Z测量,将选择告诉Charlie,Charlie需要以最小的不确定性猜出对应的测量结果,在这个游戏里,玩家Bob和Charlie 与玩家Alice 是对手,在Alice得到测量结果K并将测量选择告知Bob和Charlie后,只有在这两个玩家同时猜出结果为K时,他们两个才算赢了玩家Alice.但是从(55)式可以看出,由于测量选择X和Z的互补性,Bob和Charlie 对猜测结果的不确定性是一种此起彼伏的关系,即如果在玩家Alice 测量选择为X时,Bob 准确地猜测出了结果为K,那么Charlie就无法在Alice 测量选择为Z时,正确猜测到结果为K,反之亦然.

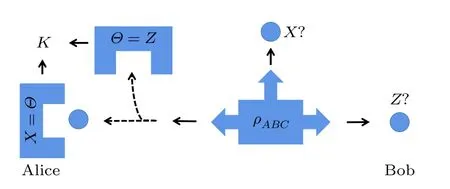
图4 三粒子量子存储器设置图.首先,粒子源准备 ρABC,并将A 发送给Alice,B 发送给Bob,C 给Charlie.接着,Alice 在A 上进行X 或Z 测量,然后在已经给Bob 粒子B 的情况下,询问Bob 关于Alice 的X 测量结果的不确定性,在已经给Charlie 粒子C 的情况下询问Charlie 有关Alice 的Z 测量结果的不确定性.只有他们两个同时猜出结果K 这个游戏才能算Bob和Charlie 胜利Fig.4.The tripartite quantum memory setup.First,the particle source prepares ρABC,and sends A to Alice,B to Bob,and C to Charlie.Next,Alice performs measurement X or Z on A,and asks Bob about the uncertainty of Alice’s X measurement outcome,ask Charlie about the uncertainty of Alice’s Z measurement outcome.Only both of them guessed that the output is K,the game can be considered a victory for Bob and Charlie.

对于Renes 的结论,会发现它的下界在两个可观测量确定下来后就是一个常量,这是有一定的局限性.于此,Ming 等[43]在Renes和Boileau 的结论基础上,得到了一个更为优化的下界,具体形式如下:

将两式结合便可得到一个新的不等式

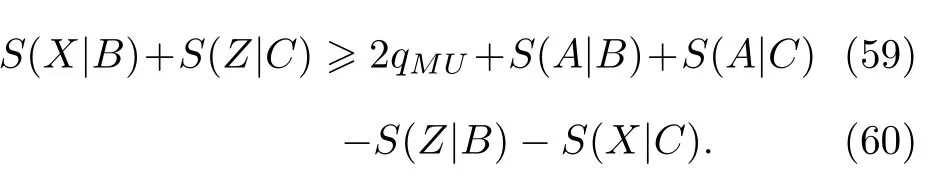
再将S(A)I(A:B)+S(A|B) ,S(A)I(A:C)+S(A|C),H(Z)I(Z;B)+S(Z|B) 和H(X)I(X;C)+S(X|C)整理,即可推出Ming 等的结果.值得注意的是,在几个特殊的情况下Δ可以被简化:1)当可观测量X和Z是完全互补且子系统A是最大混合态时,比如GHZ 态;2)当可观测量是泡利测量即σx,σz测量,子系统又是非相干态时,例如GHZ 类态、广义的W 态和Werner 类态;在这两种情况下都可以得到H(X)+H(Z)S(ρA)+qMU,那么Δ可以被简化为ΔS(ρA)-[I(A:B)+I(A:C)]+I(Z;B)+I(X;C).

随后,Dolatkhah 等[44]在Ming 等[43]的工作基础上提出了新的下界,形式如下:

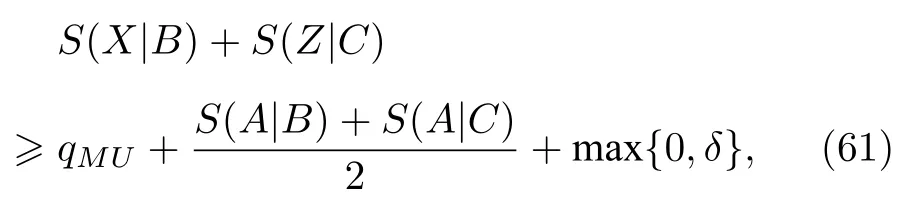
图5 这两张图引用自参考文献[44] 中的第三,四幅图,图片展示了Ming 等的结果(图上的Ref.[45]就是本文参考文献[43])和Dolatkhah 等结果的对比,这里选取的测量是泡利测量:X=σx,Z=σz .图中蓝线是式(61)左式,红线对应右式,重合表明对应的量子态、界与不确定度重合.(a) 广义W 态量子存储下的熵不确定度及下界的图像.(b)混合三比特态量子存储下的熵不确定度及下界的图像Fig.5.These two pictures are quoted in the third and fourth pictures in the reference[44].The picture shows the comparison of the results of Ming et al.(Ref.[45] on the picture is the reference[43] in this text) and Dolatkhah et al..The measurement selected here is the Pauli measurement:X=σx,Z=σz .The blue line in the figure is the left side of the formula (61),and the red line corresponds to the right side.Their overlap indicates the corresponding quantum state,and the bounds coincide with the uncertainty.(a) Different lower bounds of the tripartite quantum-memory-assisted entropic uncertainty relation(QMA-EUR) for the generalized W state;(b) Different lower bounds of the tripartite QMA-EUR for symmetric family of mixed three-qubit states.

3.3 熵不确定度关系动力学

仅仅分析熵不确定度关系本身是远远不够的,对于熵不确定度关系的研究应该落实到具体的量子系统中来,所以本节主要介绍熵不确定度关系在各类量子系统中的动力学演化.

3.3.1 马尔科夫和非马尔科夫噪声

从实际的角度出发,量子系统通常是开放系统,开放系统[45]退相干效应会或多或少地影响不确定度的大小.从这个意义上说,在量子测量中,了解环境如何影响不确定性的大小变得不可或缺和至关重要.到目前为止,在各种环境噪声下的量子存储下熵不确定度关系的研究方面已经做了大量的工作.一般来说,环境的类型可以分为马尔科夫和非马尔科夫环境.如果一个系统的信息以单向的方式从系统流向环境,没有信息回流,就说环境是马尔可夫的;相反,如果存储在中心系统中的信息是在系统和环境之间双向流动的,也就是存在信息回流的情况,则称该环境为非马尔可夫环境.

我们小组[46]在研究了在没有量子存储器的情况下,当一个量子比特经历马尔科夫和非马尔科夫的交叉时,熵不确定性的动力学.该系统由一个两能级原子与一个复合环境(一个单模腔和一个多层级热库)耦合而成.通过研究发现,腔体与热库相对较强的耦合强度可以减少不确定性.即原子与腔之间相对较强的耦合强度是产生非马尔科夫的原因,而弱耦合强度则会导致马尔可夫性.原子腔耦合强度越强,信息就会回流到原子中,具体表现为测量不确定度的振荡.值得注意的是,当原子腔的耦合强度较强于临界耦合强度时,不确定度在测得的不确定度的范围内振荡,当原子腔耦合强度小于临界耦合强度时,不确定性不断减小,并在长时间限制内达到下界.

随后,在马尔科夫和非马尔科夫交叉的情况下讨论了由两个独立耦合到结构玻色子储层的原子组成的中心系统中量子存储下的熵不确定度关系[47],该不确定关系由两个独立耦合到结构玻色子储层的原子组成.量子记忆辅助熵不确定性的动力学在马尔可夫和非马尔可夫制度中非常独特.强烈的非马尔可夫性会导致测量不确定度和下限的大幅度和长周期振荡.然而,对于马尔可夫制度,不确定性和下限会随着时间的推移先增加然后减少到一个固定值.此外,还有一些工作[48-50]来观察受非马尔可夫性影响的熵的不确定性的动力学特征.

3.3.2 几种特定的系统中的熵不确定度关系动力学

弯曲时空下系统,Feng 等[51]在2015 年首次观测到在Schwarzschild 黑洞框架中的量子存储下的熵不确定度关系,这个Schwarzschild 黑洞被认为是提供弯曲时空的一个.研究可以发现,霍金辐射可以对不确定性下界进行重要修正.对于自由落体的观察者与其拥有与待测量子子系统初始相关的量子存储器的静态合体之间的不确定性博弈,因此源于霍金辐射的信息丢失不可避免地导致不确定性量的增加.熵不确定性对黑洞的质量、量子存储器的模式频率以及观察者与黑洞表面的距离很敏感.此外,为了显示其结果的普遍性,将熵不确定度与其他不确定度测量,即Aharonov-Anandan时间-能量不确定度进行了比较.

考虑到两个静态玩家之间的不确定性博弈,Alice 持有的测量系统A和Bob 充当量子存储器的B通常可以通过一对两能级原子与黑洞外波动的无质量量子标量场相互作用来模拟.经过模拟可以注意到复合系统最终会达到平衡.事实上,子系统A的量子信息是通过它们之间产生的纠缠来传递并存储在量子存储器中的.值得注意的是,可以通过S(A|B)＜0 纠缠被目击到.

最近,Huang 等[52]研究了在Schwarzschild黑洞表面附近,有自旋和无自旋的Dirac 场方向的熵不确定度关系,证明了其边界可以用Holevo 量重写.结果表明,与互信息相比,Holevo 下界比更紧致.此外,当量子存储器离开黑洞时,不确定性和所提议的下界之间的差异不变,并且不依赖于黑洞的任何属性.此外,已经有学者[53-55]研究了在Garfinkle-Horowitz-Strominger 背景下用于Dirac粒子膨胀黑洞量子存储下的熵不确定度关系.

我们还关注了自旋链系统中的熵不确定度关系,Heisenberg 自旋链也有许多分类,一维Heisenberg 的XYZ链哈密顿量可以表示为

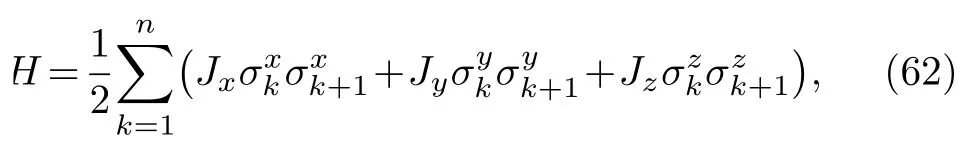
(γx,y,z)指代k位置的泡利算符,Jγ是关于自旋-自旋相互作用的实际耦合强度.如果Jz0,且JxJy,相应的Heisenberg 链称为XX模型.第一个将量子存储下熵不确定度关系应用到两比特XX自旋模型的是Huang 等[56].他们的结果表明,两个自旋量子位之间的耦合系数越大越会降低不确定度,对于相对较大的耦合系数,熵不确定度甚至会达到零.随后,在其他Heisenberg 自旋链模型和具有Dzyaloshinski-Moriya (DM)相互作用的Heisenberg 模型中,也有一些关于量子存储下熵不确定度关系的研究[57-59].

此外,团队还探讨了在非均匀磁场中一般海森伯XY Z模型中熵不确定度与量子关联之间的关系[13].值得注意的是,我们得到一个有趣的结果,(55)式中表示的下界可以改写为

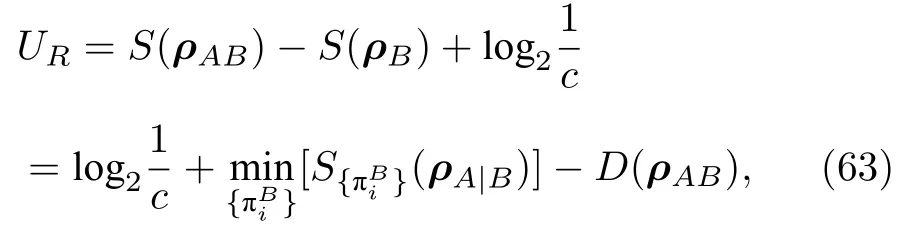
从(63)式中可以发现,下界与量子关联D(ρAB) 是成反关联的.此外,Zheng 等[60]和Huang 等[61]还研究了系统的纠缠与下界之间的关系,Heisenberg模型中具有DM 相互作用的熵不确定度的紧密性.Ming 等[62]比较了DM 相互作用的不同部分对降低熵不确定度的影响,并且发现不确定关系的下界与量子相干密切相关,但不完全依赖于量子相干.Yang 等[63]也研究了具有DM 相互作用的一般HeisenbergXYZ模型的熵不确定度的动力学特性.Zhang 等[64]和Shi 等[65]研究了高维Heisenberg模型量子存储下熵不确定度关系,最近Li 等[66]及Ju 等[67]研究了自旋混合链中的熵不确定度关系.除了上面说的两种系统,还有非惯性坐标系[68]、金刚石中的单氮空位中心[29]、中微子[69,70]等系统中熵不确定度关系的演化.

实际上在现实量子信息处理中,任何量子系统都不可避免地会与周围环境相互作用,从而导致退相干或耗散,这也会对不确定性产生影响[71],考虑到这一点,在执行量子任务时需要有效地抑制退相干.而为了获得更精确的测量结果,一些研究人员致力于追求利用各种操作如非坍缩操作[72-75]、过滤操作[76,77]、非厄米操作[78-81]等对熵不确定度进行调控.

4 不确定关系在实际中的应用

4.1 量子隐形传态

(34)式中量子存储下的熵不确定度关系也可以用来识别非经典隐形传态[82]的信道状态.基于平均隐形传态的保真度

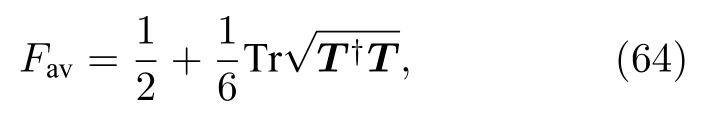
是局部酉不变的事实,同时任意两量子比特态是局部么正的,几何上表明,与没有量子记忆存储下的情况相比,任意对应于Berta 等提出的不确定下界改进的态ρAB对于量子隐形传态来说更有用.也就是说,当一个人观察到一个负的条件熵S(A|B)时,可以确定保真度能超越经典极限2/3.

4.2 导引不等式

在1935 由Schrödinger[83]首先强调,导引是一种与纠缠相关的双量子系统的现象(尽管不完全相同).考虑有两个参与者Alice和Bob 两方的远程实验室范例,他们俩各自掌握着子系统A或B.导引表示一个子系统A的测量选择可能导致另一个子系统B上的不同状态集合.并不是所有的量子态都是可导引的,举个例子,可分离态就是不可导引的.此外只要是违反贝尔不等式的态都是可导引的,贝尔不等式是根据局部隐变量模型推出的.Wiseman 等[84]将可导引的概念形式化为那些不允许局域隐态模型(LHS)的态ρAB,LHS 模型可以这样来解释,系统B有一个局部量子态,它与系统A上的任意可观测物经典地相关.这种形式化的描述使得研究人员推导出了导引不等式,与贝尔不等式类似.

Walborn 等[85]和Schneeloch 等[86]展示了如何利用熵不确定性关系来推导导引不等式.如果B有一个局部隐态,那么它的测量概率必须服从单系统的不确定性关系,即使它们是以A的测量结果为条件的.更准确地说,LHS 模型意味着A和B上的离散可观测量XA,XB的联合概率分布为

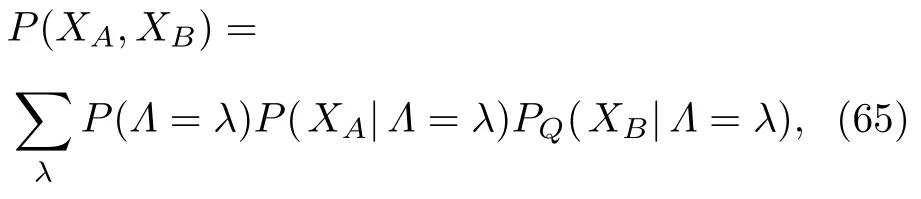
这里Λ是决定Bob 的局部状态的隐变量,λ是这个变量可以取的一个特定值,而PQ(XB|Λλ) 上的下标Q强调了概率分布来自于单个量子态.然后得到

这里的H(XB|XAΛλ)可以被解读为以XA为条件,以Λλ为条件的XB的熵.因此,对于两个在B上的可观测量XB和ZB和其他两个在A上的可观测量XA和ZA,可以得到

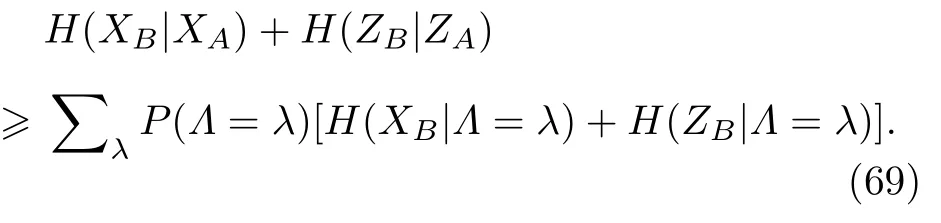
将其与Maassen-Uffink 的不确定度关系(31)式相结合,得到如下的导引不等式[86]:

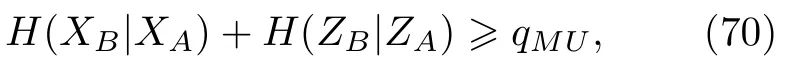
其中,qMU对应着Bob 的可观测量,任何允许LHS模型的状态ρAB必须满足(70)式.因此,(70)式的实验违反可以构成导引的演示.对于连续变量,也可以推导出类似的导引不等式[85].

Zhen 等[87]通过局域不确定原理证明了EPR(Einstein-Podolsky-Rosen) 导引.他们指出如果下面的不等式被违背,那么就说明两比特态ρAB是可导引的(A可以导引B),不等式如下:

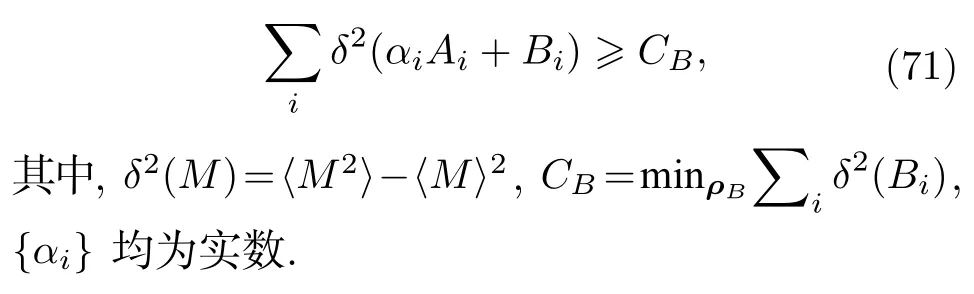
4.3 随机数

随机数是许多日常信息处理任务中的关键资源,应用范围之广可以从在线赌博到科学模拟和密码学,因为计算机被设定来执行确定性操作,所以随机数是一种稀缺资源.经典物理是确定性的,换句话来说,如果观察者对物理学系统的初始状态和在该系统上进行的操作有充分的了解,那么从原理上来说,实验的每一个结果都可以被准确地预测,而伪随机的研究试图规避这个问题[88].

量子力学固有的不确定性不允许人们去考虑随机性更强的概念,即在信息领域层面上来说,随机数是安全的.形式上,想生成一个随机变量L可以均匀分布在设定长度l上的所有位串{0,1}l上.此外,我们还希望这个随机变量独立于观察者可能拥有的任何边信息包括用于计算L的过程和任何用来准备L的随机种子.经典量子积态

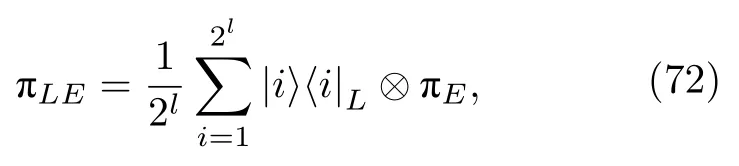
描述了独立于其环境或边信息E的l位均匀随机数.通常我们最期待的结果就是接近这个态,也就是说如果

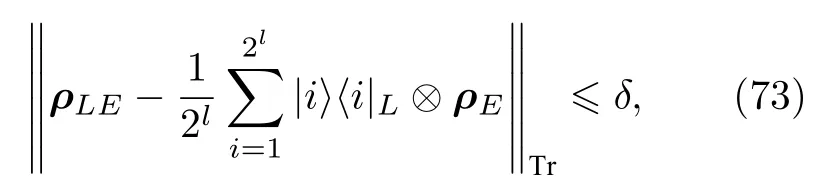
那么可以说ρLE描述了一个L是δ接近l位均匀随机数且独立于E的态,这里的‖·‖Tr代表迹范数.这个界意味着L有超过的概率不能够从一个均匀且独立的随机变量中被区分开来.这个观点是通用可组合安全框架的核心[89,90],也保证了满足此属性的密钥可以安全地用于任何需要秘钥的加密协议.

熵不确定度关系可以帮助我们实现真正的随机数.因为他们表明了量子测量产生的随机变量是不确定的.然而,为了提取近似均匀和独立的随机数,还需要一个额外的步骤,也是接下来要介绍的.

先讨论条件最小熵的现实意义.最小熵在密码学中的重要性部分归功于剩余哈希原理(leftover hashing lemma)[91-93],该原理指出,存在一个函数族{fs}s(fs:χ→[2l]),叫做哈希函数,这样,当初始的最小熵足够大时,通过应用含有均匀随机选择的种子S的函数fs得到的随机变量LfS(X) 接近均匀随机数,且与S无关.

更正式地来说,Renner[94]和König[95]展示了量子情况下的结果.对于任意Hmin(X|E)≥k的经典量子态

都存在一组哈希函数.经过应用函数fs之后的经典-量子-经典态ρLES为

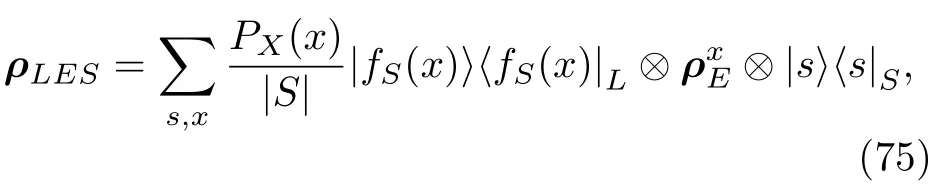
它描述的是一个态中的L是δ接近l位均匀随机数且独立于E和S,这里的.

在计算机科学中,对环境E是平凡的特殊例子进行了广泛的讨论.由于哈希是一个经典的进程,人可能认为边信息的物理性质是非相关的,且一个经典处理就足够了,事实上,这在一般情况下是不会成立的.举个例子,如果某些提取器的输入侧信息被存储在量子存储器中,那么它们的输出可能是部分已知的,同时,相同的输出几乎一致地限制了任意经典边信息,具体例子见Gavinsky 等[96]的文章.

通过考虑ε-smooth最小熵(记为其中ε ＞2) 的变化,可以对这一结果进行推广,这是通过最大化状态的最小熵来定义的,这些态处在围绕态ρ周围半径为ε的球中.推广后的剩余哈希引理[94,97,98]断言,存在一个函数族{fs}s,使得对任意≥k的 态ρXE,发 现LfS(x) 是δ+ε接近l位均匀随机数且独立于E和S,这里的δ和（75）式中定义的一样.推广后的结果在以下情况下是紧致的,即如果LfS(x) 对任意的函数族{fs}s都是ε接近均匀随机数且独立于E和S,那么就可以得到≥l,这里的由于这个紧密性结果,有理由说,平滑最小熵描述了(至少近似地)与其环境E相关的随机源X中可以提取多少均匀随机数.

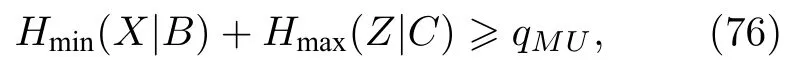
从而得出

这里的X和Z是d维希尔伯特空间中相互无偏基测量,E是被测系统的环境,最大熵Hmax(Z)H1/2(Z)可以通过统计学检验估算得出,导致了对Hmin(X|E)充满信心.正如讨论的那样,剩余哈希引理允许从X中提取均匀随机数.

Miller和Shi[100]推导出了基于熵差的下界,而不是条件熵,假设X和Z是在一个量子比特上互补的二元测量,那么下面的关系式始终成立:

这里的δ是由下面的等式得出的:

q是满足的函数.然后继续使用这个结果来限定smooth 最小熵,并继续应用到广义剩余哈希引理上.

4.4 波粒二象性

波粒二象性是指单个量子系统既可以表现出波的行为,也可以表现出粒子性行为的基本概念,无法设计出能够同时显示两种行为的干涉仪.这一观点先被Feynman 定性地讨论了,随后Wooter和Zurek[101]、Jaeger 等[102]、Englert[103]和Bergou[104]及其他学者[105]将其进行了定量的讨论,这些学者都是证明了广为人知的波粒二象性关系不等式的人.然后在Mach—Zehnder 干涉仪下,推导了单光子的一些相关关系.在所有的这些情况下,粒子性行为与已知的光子传输路径相关,当有人改变了一对干涉仪臂之间的相对相位时,波行为和在特定输出模式下探测光子的概率中看到的振荡有关,将which-path 可观测量表示为Z{|0〉〈0|,|1〉〈1|},粒子性行为可以通过路径可预测性P2pguess(Z)-1来量化,路径可预测性和精准猜测路径的概率pguess(Z)有关.波行为是由边缘可见度来量化的:

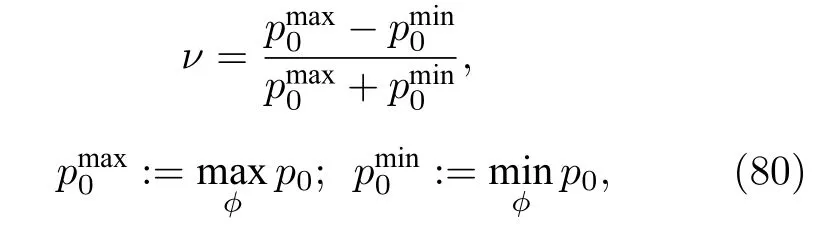
这里的p0是指光子被D0探测到的概率,可以在图6中看到.Wootter和Zurek[101]证明了

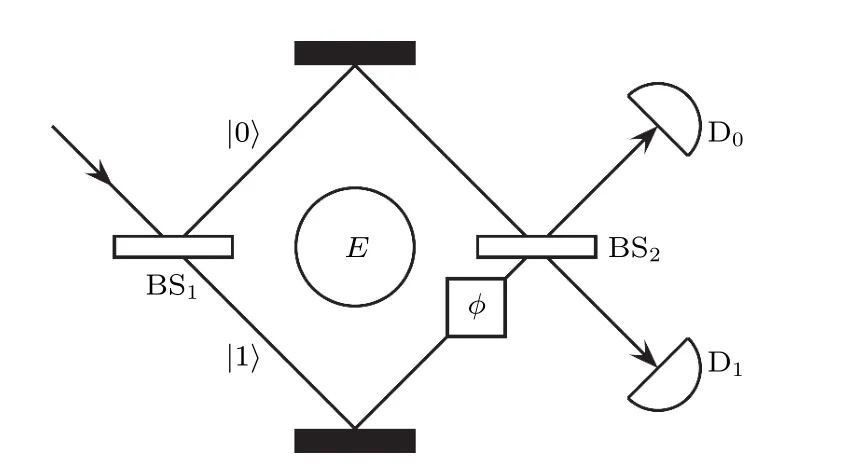
图6 这张图引用自参考文献[105]中的第18 幅图,展示的是一个Mach-Zehnder 单光子干涉仪.一个光子撞击分束器,然后通过 Z的基态|0〉,|1〉 标记这两个可能的路径,光子可能与干涉仪内部的某个环境E 相互作用.然后将一个相位φ 应用于下路径,再将这两个路径在第二个波束分束器上重新组合.最后在 D0或 D1 处检测到光子Fig.6.This picture is from the 18 th picture in the reference[105].The picture shows a Mach-Zehnder single photon interferometer.A photon hits the beam splitter,and then we pass the ground state of Z(|0〉,|1〉) to mark these two possible paths.The photon may be related to an environment in the interferometer E Interaction.Then apply a phase φ to the lower path,and then recombine the two paths on the second beam splitter.Finally,a photon is detected at D0or D1 .

即P1时,ν0 (也就是说,完全的粒子性行为就意味着没有波行为),反之亦然.

更一般地,假设光子与干涉仪内部的某个环境系统E相互作用.测量E可能揭示一些比如说关于光子路径的一些信息,所以很自然地考虑路径的可分辨性

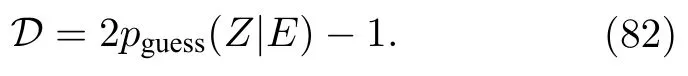
Jaeger 等[102]和Englert[103]证明了(81)式的加强版本,即:

像(81)式和(83)式的波粒二象性关系概念上经常被认为不同于不确定关系,尽管这点一直以来都存在争论.如Dürr和Rempe[106]以及Busch和Shilladay[107]发现某些波粒二象性关系与Robertson涉及标准差的不确定度关系之间存在联系.Coles 等[108]表示(81)式和(83)式以及其他一些波粒二象性关系实际上是伪装的熵不确定度关系.特别地,它们对应于(76)式中最小和最大熵不确定度关系,应用于互补量子位可观测量.即(81)式等价于不确定度关系

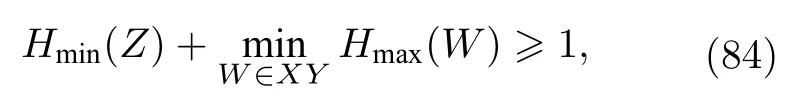
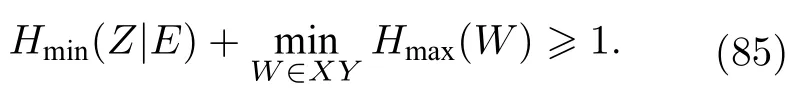
这将波粒二象性原理与熵测不准原理统一起来,说明前者是后者的一个特例.

自然地,其他熵可以用来代替最小和最大熵,虽然人们可能无法得到与波粒二象性关系的精确对等关系,但概念意义可能是相似的.Bosyk 等[109]采用了用其他熵来替代最大最小熵的方法，他利用的是包含了Rényi 熵的不确定关系.Vaccaro[110]根据互信息采用香农熵来表示波粒二象性关系.此外,还补充了一个概念,即波和粒子的行为分别与对称性和非对称性有关.Englert等[111]还考虑了具有两条以上路径的干涉仪的波和粒子行为的熵测量.

4.5 量子密钥分发

密钥分发方案的目标是让诚实的两方通过公共通道进行通信,以使密钥不被任何潜在的对手窃取,从而达成共享密钥的协议.传统上,试图共享密钥的两个诚实方被称为Alice和Bob,而窃听者被称为Eve.通过简单的对称论证,很明显,如果只考虑经典信息,密钥分配是不可能的,因为Eve会听到所有Alice 对Bob 的沟通,在协议的任意点上,她至少和Bob 拥有同样多的关于Alice 密钥的信息,如果Bob 知道Alice 的密钥,那么Eve 也知道.Bennett 等[112]首先提出量子密钥分配,随后由Ekert[113]提出了更优化方案[114].由于非复制和非克隆的量子信息特征[115],当Alice和Bob 共享密钥并通过量子信道进行通信时,对称性的论点就不再适用了.简单地说,不管窃听者什么时候与信道进行相互作用,对粒子进行测量,她的行为都会不可避免地在量子通信过程中产生噪声.因此,他们能够检测并立即终止协议.

这里先介绍一种简单的协议,采用的是删节版的Ekert[113]协议.首先准备工作:Alice和Bob 使用公共信道共享一个最大纠缠的双量子位态.Eve 可以与信道进行连续的相互作用.然后测量:他们随机同意(使用公共通道),在基Z{|0〉〈0|,|1〉〈1|}或X{|+〉〈+|,|-〉〈-|}进行,并在此基底上测量各自的量子比特(这两个步骤重复了很多次).参数评估:Alice 会公布她的测量结果.如果双方的测量结果在大多数回合中都是一致的,就可以得出结论,双方之间关联存在一些保密性,然后继续改正错误并提取一个密钥.如果没有,Alice,Bob 双方就中止协议.

针对一般性攻击的量子密钥分发安全性首先由Mayers[116],Biham 等[117],Lo和Chau[118]以 及Shor和Preskill[119]正式建立.在所有这些安全性讨论中,互补性或不确定原理以某种形式被调用来论证如果 Alice和Bob 在一个基础上测量的量子比特有很大的一致性,那么Eve 关于在互补基础上测量的比特的信息必然是低的.

熵不确定度关系首次被Cerf 等[120]和Grosshans 等[121]用于这方面.特别是Koashi 利用Maassen-Uffink 关系建立了安全性.然而,熵不确定性与量子存储器之间的关系提供了一个更直接的途径来QKD 的安全性参数进行形式化描述,如下所示.这里遵循Berta 等[9]提出的论点.首先要注意,在准备步骤中,窃听者可能会干扰,因此没有人知道在准备步骤完成后,Alice和Bob 是否确实共享最大纠缠态.然而,在不失一般性的前提下,可以假设Alice,Bob和Eve 在制备步骤后共享一个任意态ρABE,其中A和B是量子位,E是Eve持有的任意量子系统.设Θ是一个处于完全混合状态的二进制寄存器,它决定了量子位是在基X还是基Z中被测量,并用Y表示Alice 测量的输出.就可以得到和.因此,可以将具有量子存储器的三体熵不确定度原理写为

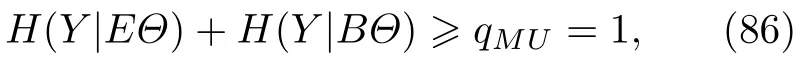
qMU1是基于测量基X和Z得出的.在对Alice量子位进行测量后,对态ρYΘBE进行熵的计算.接着再对B进行测量,这会产生一个Y中的估算,再根据数据处理不等式可以得出H(Y|BΘ)≤H(),因此总结得出H(Y|EΘ)≥1-H() .这就保证了只要条件熵H() 很小,Eve 对于Alice测量结果的不确定度(就von Neumann 熵而言)就会很大.这就是安全准则的量化表达.

除上述应用外,还有许多其他重要的应用,比如两方密码学[122-124]、纠缠目击[125,126]等,还有熵不确定度关系与量子相干[127-130]、量子纠缠[131]、失谐[30-32,132]等之间的联系.

5 结论与展望

本文从海森伯测不准原理出发,追溯了熵不确定度关系的历史,讨论了海森伯不确定原理和它的各类衍生关系式及其最新进展.首先从标准差、熵和优化方法的角度回顾了不确定关系,接着又着重介绍了量子存储下熵不确定度关系的发展,这些关系与许多量子信息处理任务直接相关.许多学者仍在探索不确定关系,各种新的工具不断被拿来并试图推出新的不确定关系.如Majorization 方法,用Majorization 方法来度量不确定度仍有很大的发展前景;关于量子存储下熵不确定度关系,Dupuis等[123]在2015 年建立了推导不确定关系的元定理.但据了解,并不是所有体系推出的不确定关系都很紧致,因此也需要进一步改善加强.

本文提到的各种技术应用如量子密钥分发等为获得更精细的熵不确定度关系提供了动力.例如,要证明涉及两次以上测量的量子密钥分发协议的安全性,就需要新的熵不确定度关系,即允许量子存储和多次测量的熵不确定度关系.这是一个需要更多研究的重要前沿领域.与设备无关的随机数,即证明从不可信的设备获得的随机数是另一种新兴应用,熵不确定度关系在这方面应该是很有潜力的.

对于熵的不确定度关系,除了对各种技术应用有着推进作用,它还让人们对基础物理学有了更深的了解.如熵的不确定度关系使不确定原理与波粒二象性原理统一起来.将熵不确定度关系应用于干涉仪,很可能成为量化波粒二象性的一个自然框架,同样,量子基础的一个热门话题是测量不确定性.也可以将制备不确定度的概念与可逆性测量相结合[133],相应的熵不确定度关系在IBM[134]量子实验上测试成功,不确定关系在实验研究方面也有着相当多的进展[135-137].除上述以外,熵不确定度关系可能在凝聚态物理的相变研究[138,139]中发挥作用,也在狭义和广义相对论的背景下[140,141]进行了研究.鉴于量子信息在宇宙学中[142]扮演着越来越重要的角色,希望在未来,熵不确定度关系在宇宙学等相关背景下有着进一步的发展.期待不确定度在未来得到更多的关注,在学者们的共同努力下取得一些新的成果.