二维各向异性SSH 模型的拓扑性质研究*
郭思嘉 李昱增 李天梓 范喜迎 邱春印
(武汉大学物理科学与技术学院,武汉 430072)
二维Su-Schrieffer-Heeger(SSH)模型是在拓扑物理领域受到广泛研究的一种模型,具有许多独特的物理性质.它属于高阶拓扑绝缘体,在第二条和第三条能带间会产生具有连续谱束缚态(bound states in the continuum,BICs)性质的角态.本文首先介绍了二维SSH 模型的拓扑性质,在此基础上论证了第二条和第三条能带何时会在整个布里渊区上产生能隙.随后,计算了模型的电荷极化分布和电荷密度分布,证明了当x 方向上胞内跃迁几率和胞间跃迁几率较大时,x 方向的边缘电荷极化激发了y 方向的边缘态,反之亦然.同时,边缘电荷极化激发了角上的异常填充,产生了具有良好局域性与鲁棒性的拓扑角态.最后,构建了一种声学谐振腔模型,并证明了该模型可以较好的模拟各向异性二维SSH 模型的拓扑性质.
1 引言
拓扑学是数学领域的一个重要分支,主要研究几何图形或空间在连续形变下的不变性质.拓扑学进入物理领域的标志是凝聚态物理中整数量子霍尔效应的发现:1980 年Klitzing 等[1]在强磁场中第一次发现了量子化的霍尔电导,紧接着在1982 年Thouless 等[2]指出霍尔电导来源于能带的非平庸拓扑性质.量子化霍尔电导的发现赋予了拓扑学全新的物理意义,由此拓扑物理学作为一个新兴领域得到了广泛关注.在拓扑学研究中一般用拓扑不变量描述拓扑物态的性质:当两种具有不同拓扑不变量的界面接触时,会产生空间局域化的边界态.除非带隙关闭,系统的拓扑不变量在扰动或变形下保持不变,因此拓扑保护的边界态具有抗边界无序的鲁棒性和单向传播的边缘态等新颖的物理性质[3-9].用于描述聚乙炔原子链的一维Su-Schrieffer-Heeger(SSH)模型是具有非平庸拓扑性质的最简单模型,它是一种具有交错跃迁几率的无自旋费米子模型,特点是当胞间跃迁几率v大于胞内跃迁几率w时,会产生一对局域在有限长SSH链两端点的态,即拓扑孤子态;当v小于w时,拓扑孤子态消失.这一现象可由拓扑不变量“缠绕数”(winding number)进行描述:当v >w时,缠绕数为1,体系对应拓扑非平庸;当v<w时,缠绕数为0,体系对应拓扑平庸.这两种不同的拓扑相不能在不关闭带隙的前提下绝热地相互转换.
近年来随着对拓扑物态的进一步研究,人们提出了高阶拓扑绝缘体(high order topological insulators,HOTIs)的概念[10,11].高阶拓扑绝缘体的“高阶”主要体现在其独特的体-边界对应关系上.对于d维的传统拓扑绝缘体,一般具有 (d-1) 维边界态;而d维的n阶拓扑绝缘体具有 (d-n) 维边界态,n满足 1≤n≤d.研究表明,作为一维SSH 模型的扩展,在二维方向具有跃迁几率交替变化的体系可拥有高阶拓扑特性.典型的代表包括电四极子模型、Kagome 晶格模型、方形晶格模型等[12-27],它们可支持零维的角态[28,29].对于这类模型,早期的研究集中于其第一、二条(或第三、四条)能带间的边缘态与角态[30-36];最近,随着研究的深入,人们发现了在第二条和第三条能带之间的角态.特别地,当模型具有手性和C4对称性时[37-41],这种角态是一类连续谱束缚态(bound states in the continuum,BICs)[42-51].因此,对于这种角态的拓扑性质的系统性研究显得尤为必要.
高阶拓扑绝缘体的拓扑相变已经有了一套标准化的描述方法,如通过威尔森循环(Willson loop)方法计算电四极矩(三维模型为电八极矩),从而得到其电荷极化与分数电荷.又如通过计算的Zak phase 来区分不同的拓扑态.但以上的方法都有其局限性,无法解释二维SSH 模型中角态是如何产生的.就此,本文主要做了以下工作:1) 打破二维SSH 模型的各向同性,并在各向异性体系中,找到了第二条和第三条能带间存在完全带隙的情形;2) 在带隙打开的前提下,通过求解半无限大条带模型的混合瓦尼尔函数问题计算系统的电荷极化空间分布,并进而计算电荷密度分布,寻找其与电荷极化分布的对应关系;3) 验证了边缘电荷极化与分数电荷(fractional charge)和二维SSH 模型中分布于能隙内部的边缘态与角态的对应关系,以此为依据解释了这类边缘态与角态的产生机理;4) 构建了一种声学谐振腔模型,并通过改变谐振腔之间导管的直径来控制格点之间的跃迁几率,从而使其可以模拟不同参数的SSH 模型.最后计算证明其确实可以模拟各向异性二维SSH 模型的拓扑性质.
2 二维方形晶格SSH 模型
2.1 二维SSH 模型简介
一般的二维SSH 模型示意图如图1(a),阴影区域代表单个原胞的范围,wx,wy代表各原子间x方向和y方向的胞间跃迁;vx,vy代表x方向和y方向的胞内跃迁.我们给出一般二维SSH 模型在坐标空间中的哈密顿量:

图1 (a) 二维SSH 模型原胞示意图;(b) 二维SSH 模型在倒空间的示意图;(c) 二维SSH 模型的相图.图中黑色,绿色,蓝色五角星标记了三种典型的拓扑相,其代表的参数(α,β)分别为 (1.5,3),(2,3),(2.5,3) ;(d)图1(c)中黑色五角星代表的模型的带结构图,红色圆形标记了高对称点X 上第二条和第三条能带的变化过程;(e) 绿色五角星代表的模型的带结构图;(f) 蓝色五角星代表的模型的带结构图Fig.1.(a) Schematic diagram of the original cell of the 2D SSH model;(b) schematic diagram of the 2D SSH model in inverse space;(c) phase diagram of the 2D SSH model.The black,green and blue pentagrams in the figure mark the three typical topological phases with the parameters (α,β)as (1.5,3),(2,3)and (2.5,3) respectively;(d) a diagram of the band structure of the model represented by the black pentagram in Fig.1(c),and the red circles mark the evolution process of the second and third energy bands at the high symmetry point X;(e) band structure for the model represented by the green pentagram;(f) band structure for the model represented by the blue pentagram.

其中a,b,c,di,j标定了x方向第i个原胞和y方向第j个原胞中的4 种不同原子.令h.c.为0,对其进行傅里叶变换,可以得到动量空间中的哈密顿量:

求解其本征值问题可得到色散关系:

二维SSH 模型的第一条能带与第二条能带间存在着拓扑边缘态,其拓扑性质由胞内跃迁与胞间跃迁的比值决定:1) 当vx/wx >1 且vy/wy >1时,存在沿x方向和y方向分布的边缘态;2) 当vx/wx >1且vy/wy<1或vx/wx<1且vy/wy >1时,存在沿y方向或沿x方向分布的边缘态;3) 当vx/wx<1且vy/wy<1,不出现边缘态[52].
2.2 二维各向异性SSH 模型中的拓扑相变
改变模型的参数,即控制wx与wy,vx与vy的比例,可以打开第二条能带和第三条能带间的带隙.在这一过程中存在着拓扑相变,当带隙完全打开时,会发现存在着国定在零能处的角态.
首先需要确定拓扑相变会在何时出现.我们构建了一组参数α和β,在保持wy1 的同时令

可以看出:若wx >wy,则α >1,α越大,代表各向异性越强;若wy >wx,则 0<α<1,α1 时模型为各向同性.同时β越大,代表模型的拓扑性质越强,β<1时模型为拓扑平庸态,β >1 时模型为拓扑非平庸态.
我们规定跃迁几率为正实数,以α和β为参数,画出的所有可能存在模型的相图,如图1(c).所有模型被分为三种相:相①中带隙打开且存在角态,相②中带隙关闭,相③代表模型处于拓扑平庸,角态不存在,在本文中不予以讨论.由(2)式可知:
若wx >wy第二条能带与第三条能带的色散关系式为

若wx >wy,第二条能带与第三条能带的色散关系式为
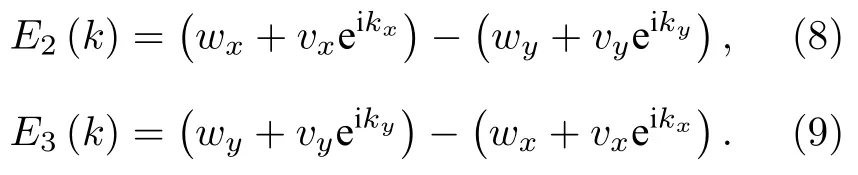
若wx >wy,若需要确保整个布里渊区内带隙打开,只需要满足在高对称点X处E3(k)>E2(k),将α,β带入,可得

若wx >wy,同理可得

这便是相①和相②右左两条边界曲线的表达式,两者与α1 相交于无穷远处.显然在相①和相②边界上存在拓扑相变的过程,在这一过程中第二条能带与第三条能带能带间的带隙逐渐打开.我们在相图中挑选3组具有代表性的参数来描绘这一过程:相②;相①和相②的相边界;相①,分别以黑色,绿色和蓝色五角星标记.其参数(α,β)分别为 (1.5,3),(2,3),(2.5,3) .由(2)式,作出它们在布里渊区内的色散关系图,如图1(d)、图1(e)和图1(f)所示.在图1(d)中,第二条能带和第三条能带有两个简并点,而在图1(e)中只剩下一个,在图1(f)中简并点完全消失,带隙完全打开,这与我们推导出的结论相符.
3 边缘电荷极化与分数电荷
3.1 电荷极化分布的计算方法
虽然对于二维高阶拓扑绝缘体的研究已有一套行之有效的方法,但它们在解释该角态产生机理时都存在着困难.例如,之前的研究中已经证明,通过威尔森循环法计算不同参数下二维SSH 模型的Zak phase,可以发现当占据能带数目为1 时,图1(c)中相②与相③(即拓扑非平庸态与平庸态)的Zak phase 不同,这一结果可以解释第一条能带与第二条能带间边缘态的成因.但当占据能带数目为2 时,如表1 所列,可以看到Zak phase 始终为0.由于该角态是电子占据的第一条能带和第二条能带共同作用的结果,因此相①和相②间的拓扑相变无法通过计算Zak phase 得到较好的解释.
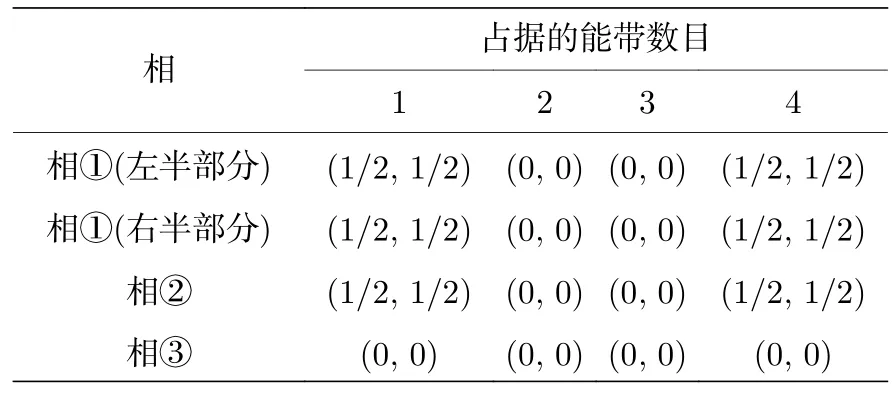
表1 运用威尔森循环法计算二维SSH 模型Zak phase 的结果Table 1.Results of the two-dimensional SSH model Zak phase using the Willson Loop method.
Benalcazar 等[53]也于2017 年提出了一种通过电四极矩计算电子极化与角分数电荷的方法,并成功解释了电四极子中的拓扑现象.但将模型量子化时,需要满足两个条件:1) 至少要有两条被占据能带;2) 保护体偶极矩的对称性需要消失.他们通过在紧束缚模型中引入负数跃迁几率从而解决了这一问题,但这也意味着该方法无法直接地被套用在二维SSH 模型上.
我们采用另一种方法来计算二维SSH 模型的电荷极化的空间分布[54,55].首先考虑一y方向上有Ny个格点的二维晶格,为了计算x方向的电荷极化分量(该分量是一以y坐标为参量的方程),让该模型具有沿x方向的周期性边界条件.由此可给出系统哈密顿量:

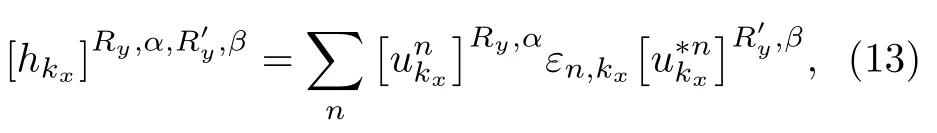
其中n∈1···Norb×Ny.假设该二维布洛赫哈密顿量具有沿y方向变为开放边界,并存在Nocc条被填充能带,其对应的赝一维哈密顿量hkx有Nocc×Ry条被填充能带.依此,(5)式中的哈密顿量可对角化:

其中

由此可以给出混合瓦尼尔方程:
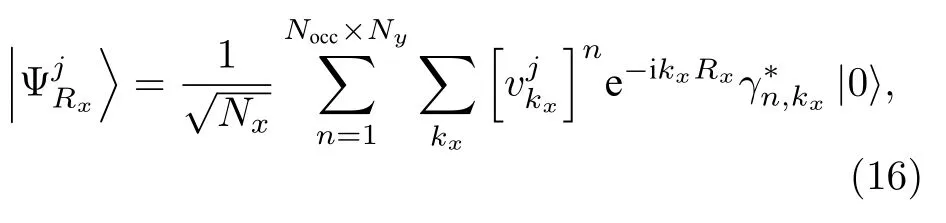

这可以让我们解决(9)式中的沿y方向的混合瓦尼尔函数问题.特别地,它让我们可以确定电荷极化是否局域在某一确定格点,即Ry处.电荷极化x方向分量为

对y方向分量,同理有
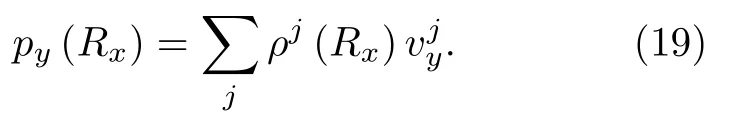
使用Matlab 软件对模型进行计算.在计算前,需要对模型哈密顿量进行修正:
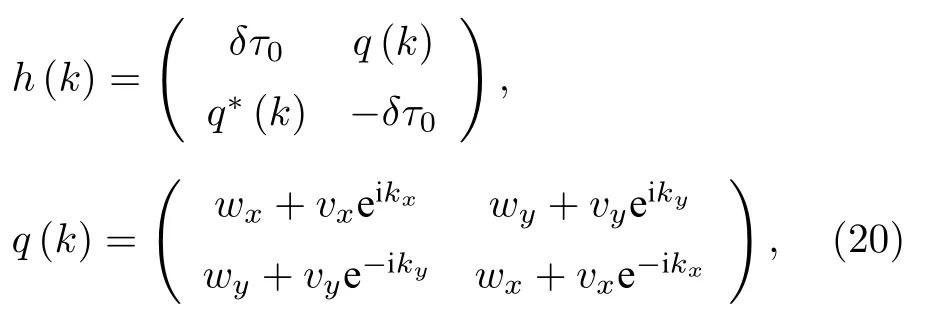
其中τ0为 2×2单位矩阵.与(1)式中的H(k) 不同,h(k)中存在着在位能±δτ0,因为在半填充状态下,体带的负能量部分和四个角态中的两个已被填充,需要一无限小的在位能±δτ0历经一系列绝热变化来打开角态处的简并.δτ0的符号决定了哪一条对角线上的角态被填充.以下统一取δ1×10-4.
为了保证边缘电荷极化和角分数电荷存在,选区的参数应位于相①中,同时α和β值应尽可能大以加宽能隙,便于观察态分布状况.选取参数(α,β)(5,4).作为对照,计算了一种拓扑平庸的情形,使用参数为 (α,β)(5,0.25) .实际计算结果如图2(a)和图2(b)所示:在y方向上,py始终为0;在x方向上,仅当Ry1 或Ry20时,px1/2(由于在位能δτ0的存在,计算时会有轻微误差),说明此时电荷极化大小为1/2 且仅分布在x方向两端,即模型的边缘上.以下记这类分布于边缘的电荷极化为.而在拓扑平庸的情形下,电荷极化无论在哪个方向上都为0.
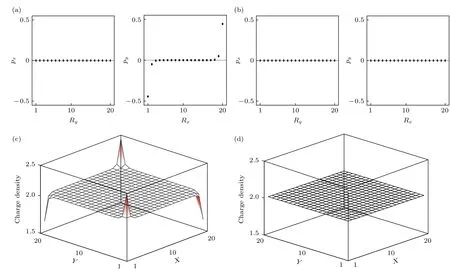
图2 电荷极化与电荷密度分布计算结果 (a) 电荷极化分布计算结果.使用的参数为 α=5,β=4,计算中使用了半无限大的条带模型,开放边界的一侧计算了有20 个原胞,从左至右分别为电荷极化的x 方向分量和y 方向分量;(b) 拓扑平庸态下的电荷极化分布.使用的参数为 α=5,β=0.25 ;(c) 电荷密度分布计算结果,计算中使用了20×20 个原胞;(d) 拓扑平庸态下的电荷极化分布Fig.2.Calculation result of polarization and charge density distribution:(a) Calculated results of the polarization intensity distribution.The parameters used are α=5,β=4,a semi-infinite strip model is used,and there are 20 primary cells on the side of the open boundary.From left to right,for the x-and y-directional components of the polarization;(b) calculated results of the polarization intensity distribution in topological trival phase.The parameters used are α=5,β=0.25 ;(c) calculated results of the charge density distribution,20×20 unit cells used in the calculation;(d) calculated results of the charge density distribution in topological trival phase.
由于模型本身的C2v对称性,vy >vx时有相似的结论:x方向上不存在边缘电荷极化;y方向上存在着1/2 的边缘电荷极化.事实上,只要模型处于图1(c)的相①中,就会存在大小为1/2 的边缘电荷极化.
3.2 电荷密度分布与分数角电荷
接下来将周期性边界条件替换为开放边界条件,假设此时存在Nx×Ny个格点.在开放边界条件下,边缘电荷极化会被另一方向的开放边界截断,从使电荷在各边界两端,即四角上累积.这一结论可以通过计算电荷的空间密度分布加以验证.定义第 (Rx,Ry)个原胞波函数为un(Rx,Ry,ς),其中ς标定了原胞中的一个格点.电荷密度分布定义式为

其中un(Rx,Ry,ς)是第n个本征态|un〉的分量.依据上式,计算模型的电荷密度分布,如图2(c)和图2(d)所示.通过计算结果可知,每个原胞内存在着作为背景的 2e电荷密度,这是由于二维SSH 模型是一类半填充模型,每个格点贡献了1/2 个电子.除此之外,在四角上电荷密度会发生大小为1/2 突变,将其记为Qcorner.而在拓扑平庸的情形下,电荷密度不会发生突变.
3.3 分数电荷与边缘电荷极化的关系
从图2(c)不难验证角电荷Qcorner与边缘电荷极化存在着对应关系:.这一点可以加以证明:电荷密度ρ定义为偶极矩密度p的负散度:

Qcorner是ρ在整个平面上的积分

化简过程中使用了斯托克斯定理(Stokes theorem).由以上计算结果可知,在二维各向异性SSH 模型中,电荷极化全部分布在边缘上,故存在:
这一结果说明在二维各向异性SSH 模型中,Qcorner完全由边缘电荷极化所产生.
4 边缘态与角态的生成机理
接下来我们希望验证当能隙打开时,边缘电荷极化与角电荷同拓扑边缘态与角态具有怎样的对应关系.使用Matlab 软件,运用紧束缚原理,计算一具有 20×20 个原胞的模型的态密度分布.计算结果如图3(a)所示,可以看到第二条和第三条能带的能隙中存在着角态和边缘态.我们也计算了x方向和y方向的投影能带,如图3(b)和图3(c)所示.图3(c)显示位于带隙内部边缘态的沿y方向分布,需要注意的是,图3(b)显示沿x方向也存在着边缘态,且位于第一条能带与第二条能带和第三条能带与第四条能带内部.由于模型满足手性对称,两类边缘态关于零能对称分布,且角态固定在零能处.最后分别计算了体态,y方向边缘态及角态的局域密度分布,结果如图3(d)、图3(e)和图3(f)所示.图中各格点上的强度是对所有存在的体态、边缘态或角态中同一格点上强度的归一平均.
由此可以总结:当边缘上存在着1/2 的电荷极化时,会观察到对应方向的边缘态;同时,存在分数角电荷时,会观察到固定在零能处的角态.对此我们给出一种解释:根据拓扑多极子绝缘体理论,存在边缘电荷极化时,电荷会在晶格的边界处聚集.对于所有被占据的能带,这种效应会等效于在电荷极化的分布方向上产生偶极矩,从而激发拓扑边缘态.值得注意的是,虽然,但如图3(b)所示,在第一条与第二条能带及第三条与第四条能带间仍存在着x方向边缘态.这是由于在计算边缘电荷极化时考虑了第一条能带和第二条能带的共同作用.而这类边缘态由于仅受第一条能带或前三条能带(由于手性对称,两者等同)产生的电荷极化影响,因此不适用该结论.
同时边缘电荷极化在全开放边界下会产生分数角电荷.在经典的无自旋且具有时间反演对称性体系中,具有Cn对称性的二维拓扑晶格绝缘体(topological crystalline insulators,TCIs)的分数角电荷与异常填充(filling anomaly)有关:这是TCIs 的一种固有拓扑属性,其产生机理源自满足电中性和晶体旋转对称性所需的电子数量间的不匹配.二维SSH 模型具有C4或C2对称性(各向异性模型为C2对称性),由于该体系处于半填充状态,每个原胞只提供两个电子,为了维持自身的晶体对称性在角上会自发地出现1/2 的分数电荷.这类分数电荷激发了如图3(f)所示的角态.由于晶格对称性的约束,该角态会被束缚在原位,因此这类角态具有很好的鲁棒性(robustness):一旦发生偏离,其强度会很快衰减为0.
5 声学模拟
尝试利用一组相互连接的声学共振腔来模拟二维SSH 模型.单个的方形共振腔代表了单一格点,胞内跃迁用共振腔间的水平方形中空导管代替.假设共振腔的外壁是极薄的,并满足刚性边界条件,则声波在共振腔内部会以驻波的形式传播并不产生耗散.在x,y,z方向上,都会产生无穷多组相互独立的本征模,大小为各方向基频的整数倍.
谐振腔长宽皆为r100 mm,高H340 mm .由于H ≫r,可以仅考虑z方向上的z1模,其频率为 500 Hz(声速c340 m/s).以最近邻方式连接的四个共振腔代表了二维SSH 模型的一个原胞,如图4(a)所示.单个原胞为一边长为a800 mm 的正方形,两谐振腔中心的距离为 1/2a.四种不同粗细的导管代表了四种不同的跃迁,分别为44 mm(代表wx),88 mm(代表vx),20 mm(代表wy),40 mm(代表vy).各方向跃迁几率大小大致与导管直径的平方成正比,这意味着该模型代表的原胞满足 (α,β)(5,4),与理论计算所用模型一致.
我们在x方向和y方向添加周期性边界条件,计算其带结构,如图4(b)所示.从图4(b)可以看到,此时第二条能带与第三条能带间的带隙打开,同时整体带结构关于500 Hz 呈镜面对称.还计算了该模型的态密度分布,如图4(c)所示,可以看到模拟计算结果与图3(a)基本一致.在态密度分布图中挑选有代表性的体态,边缘态与角态,作出它们的声压场分布图,如图4(d)—(f)所示,可以看到其与理论计算的强度分布吻合的很好.这说明该声学谐振腔模型不仅可以模拟二维SSH 模型,次级跃迁对计算结果的影响也比较微弱,能够较好的符合紧束缚近似.
6 结论
本文研究了各向异性二维SSH 模型的拓扑性质,并在此基础上探讨了一种打开第二条能带和第三条能带的简并,在整个布里渊区上生成完全带隙的可行方案.在此基础上,通过求解半无限大条带模型的混合瓦尼尔函数问题来计算电荷极化分布.计算结果显示,电荷极化仅分布在跃迁几率较大的方向的边界上,大小恒为1/2.同时还计算了电荷密度分布,观察到能隙打开时,电荷密度在四角上存在着大小为 1/2e的突变,进而发现电荷极化与偶极矩存在着对应关系:,这说明角电荷完全由边缘电荷极化产生.据此,我们给出了一种用于解释各向异性二维SSH 模型中拓扑边缘态与角态产生的理论:引入各向异性后,边缘偶极矩激发了拓扑边缘态;同时在开放边界下,边缘偶极矩会使电荷聚集在角上,从而诱导拓扑角态的产生.这类分数角电荷属于异常填充,是模型为了同时保持电中性和自身的晶格旋转对称性而自发形成的.异常填充产生的分数角电荷具有较好的局域性与鲁棒性,这类性质使得此类模型可能在定向传导以及精确信号传播等领域具备较好的应用前景.最后,构建了一种声学谐振腔模型,并运用Comsol 计算,证明了它可以在紧束缚近似下较好的模拟各向异性二维SSH 模型的拓扑性质,这为该模型在声学及声子晶体方面的应用找到了一种可能的途径.

