高分十四号卫星双线阵相机高精度在轨几何标定
卢学良,王建荣,杨秀策,吕 源,胡 燕,魏永强,曹彬才
1. 地理信息工程国家重点实验室,陕西 西安 710054; 2. 西安测绘研究所,陕西 西安 710054
高分十四号卫星于2020年12月6日成功发射,同高分七号一样均是用于1∶1万比例尺测图的亚米级高分辨率光学传输型立体测绘卫星[1]。通常,测绘卫星在发射之前,相机参数都要在实验室进行严格的几何标定,但受卫星发射振动和长时间在轨飞行中温度变化等因素的影响,各载荷之间的刚性结构和航天相机的几何参数会发生变化,影响卫星影像定位精度。因此测绘卫星需要在实验室标定参数的基础上通过在轨几何标定实现高精度定位[2-3]。
国外卫星在轨几何标定开展得比较早,美国的IKONOS、GeoEye、WorldView,法国的SPOT、Pleiades,日本的ALOS-1等卫星均采用地面几何检校场进行在轨几何标定。文献[4—6]采用FAM(field angle map)标定方法,对IKONOS、GeoEye-1、WorldView-3等卫星的相机进行了在轨标定,其中WorldView-3卫星还采用附加参数的自检校区域网平差对相机光学畸变参数进行了评估。文献[7]分别对SPOT-5卫星HRG、HRS相机进行了在轨几何标定,在垂轨和沿轨方向分别用多项式补偿后,相机内部畸变误差优于1个像素。文献[8]针对Pleiades卫星开展了几何标定试验,其影像内部畸变随着控制点使用数量的增多有一定的改善。文献[9]通过分析ALOS-1卫星系统成像特点,针对前、正、后3个线阵CCD相机设置了30个参数,采用附加参数的自检校区域网平差方法进行了标定。
2010年以来,随着天绘一号[10]、资源三号[11]等多颗光学传输型立体测绘卫星的成功发射,我国开始对测绘卫星在轨几何标定进行系统而深入的研究。关于相机参数在轨标定目前大致上有两种主流的方法,一种是天绘一号卫星工程中应用的整体标定方法,即采用三线阵相机重组的思路,将所有相机的参数作为未知参数在光束法平差中统一答解,通过该方法卫星的无控直接前方交会定位精度从200 m左右提升至9 m左右[12-14];另一种是资源三号卫星工程中应用的基于指向角的内标定和基于旋转矩阵的外标定方法,通过该方法卫星的无控直接前方交会定位精度从1000多m提升至15 m以内[15-20]。
总体来看,上述标定方法在卫星工程实践中都取得了比较好的效果。对于立体测绘卫星(双线阵或三线阵)而言,测绘相机之间的交会角是影响高程精度的重要因素,将测绘相机作为整体考虑,对相机标定参数进行整体解算,在高程定位精度上具备一定的优势[12]。
本文针对高分十四号卫星载荷特点,以双线阵立体影像为基础(不含激光测距数据),利用等效框幅思想[21-23]将双线阵前后视相机统一等效变换为垂直摄影的框幅相机,在卫星成像严密几何模型中顾及星地相机夹角系统常差和线阵不平行性,构建了在轨几何标定严密成像模型;基于宁夏1∶2000数字化定标场,采用前方交会与后方交会交替迭代的方式对双线阵相机标定参数进行整体解算,实现了高分十四号卫星双线阵相机高精度在轨几何标定,并利用全球多处检测场对标定结果进行了检测试验。试验结果表明,经双线阵相机在轨几何标定后,高分十四号卫星无地面控制条件下直接前方交会精度达到平面2.34 m(RMS),高程1.97 m(RMS)。
1 在轨几何标定流程
本文在轨几何标定流程如图1所示,主要分为如下4个步骤:
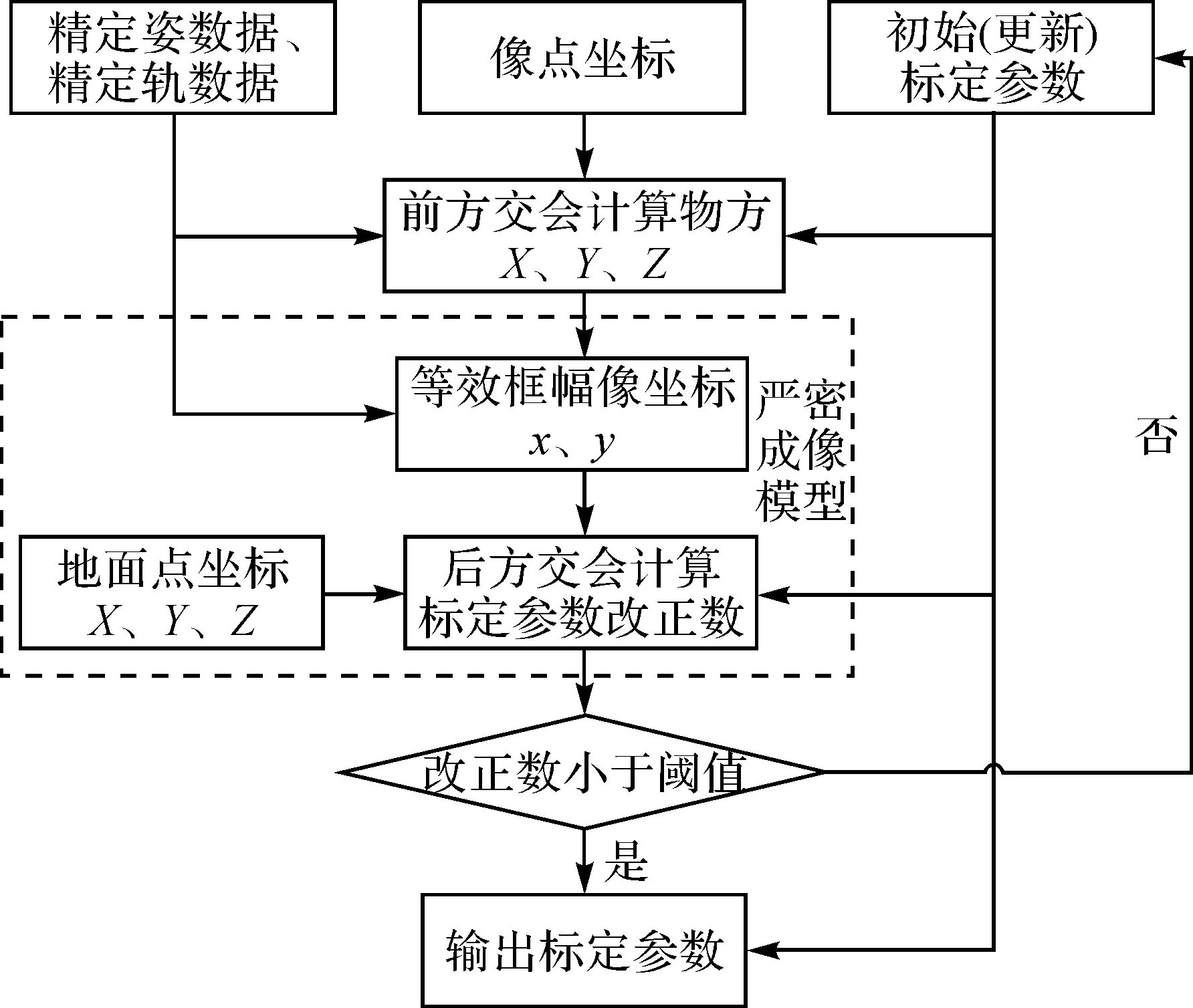
图1 在轨几何标定流程Fig.1 On-orbit geometry calibration process
(1) 利用精密定姿数据、精密定轨数据、初始标定参数和像点坐标,通过直接前方交会计算像点对应的物方坐标。
(2) 利用像点对应的物方坐标反算等效框幅像坐标。
(3) 基于在轨几何标定严密成像模型构建的误差方程,利用等效框幅像坐标、像点对应的地面点坐标通过后方交会的方式解算标定参数改正数。
(4) 如果改正数大于阈值则利用改正数更新标定参数,并重复步骤(1)—步骤(3),如果改正数小于阈值则输出标定参数。
在轨几何标定流程中的在轨几何标定严密成像模型是以共线条件方程为基础,描述地物点影像坐标(x,y)和地面坐标(X,Y,Z)之间数学关系的表达式[24],下面具体阐述在轨几何标定严密成像模型的构建过程。
2 在轨几何标定严密成像模型
2.1 双线阵相机等效变换
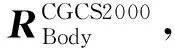
双线阵相机通过等效框幅思想进行等效变换,等效框幅思想的原理就是将线阵影像的像坐标转化为定向时刻的等效框幅像坐标,建立起等效框幅像坐标与地面点坐标之间的数学关系。根据等效框幅思想,将双线阵前后视相机统一等效变换为垂直摄影的框幅相机,等效框幅相机的相机坐标系与卫星本体坐标系的三轴指向基本一致,坐标原点为等效框幅相机的投影中心。据此构建高分十四号卫星成像严密几何模型为

(1)
式中,x=Ffsinθf、y=Fbsinθb,f=Ffcosθf、Fbcosθb,θf和θb分别为前视、后视相机倾角,Ff和Fb分别为前视、后视相机焦距;(XP,YP,ZP)和(XC,YC,ZC)分别为地面点P和卫星质心C在CGCS2000坐标系下的坐标;m为比例因子;(ΔX1,ΔY1,ΔZ1)和(ΔX2,ΔY2,ΔZ2)分别为卫星质心和相机投影中心在卫星本体坐标系下的坐标。
2.2 星地相机夹角系统常差修正
星地相机夹角变化是影响定位精度的重要因素,在相机参数标定过程中需对星地相机夹角进行标定,修正姿态系统的常差变化。对式(1)作变形,令
(2)
将式(2)代入式(1),变形有
(3)
星地相机夹角系统常差修正实际上就是引入一个正交旋转矩阵去消除由于姿态测量、载荷安置等综合因素导致的姿态系统误差。正交旋转矩阵由3个旋角φ、ω、κ按YXZ轴转序构成,记为R(φ,ω,κ)。引入星地相机夹角系统常差修正后,在轨几何标定严密成像模型如式(4)所示
(4)
2.3 顾及线阵不平行性的内方位元素建模
双线阵相机等效变换后,相机坐标系与卫星本体坐标系的三轴指向一致,即Z轴指向星下点,X轴指向飞行方向,Y轴与X轴、Z轴构成右手系。对于等效框幅相机而言,若前后视的线阵是平行的,可以将线阵的旋转误差等效到星地相机夹角系统常差修正中。高分十四号卫星双线阵影像分辨率0.6 m,幅宽40 km,线阵长度极长,虽然采用光学拼接,但受载荷安置、卫星发射振动等因素的影响,前后视的线阵难以保证相互平行,因此内方位元素建模除考虑常规的主点、主距外,还需要顾及线阵的不平行性。
在式(4)中,令
(5)
将式(5)代入式(4),则有
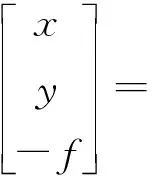
(6)
进一步,令
(7)
则有
(8)
通常线阵的不平行性只在二维空间中考虑,即只顾及焦平面中线阵的旋转[15,17],但这对1∶1万测绘卫星来讲会较大程度地影响其定位精度。因此除考虑线阵在焦平面,即绕Z轴的旋转外,还必须考虑线阵垂直于焦平面,即绕X轴的旋转,则在轨几何标定严密成像模型如式(9)所示
(9)
式中,x′、y′为修正后像点坐标;α为线阵绕Z轴的旋转角;γ为线阵绕X轴的旋转角;β为线阵绕X轴、Z轴旋转对像点坐标y的影响因子。将式(8)代入式(9)有
(10)
2.4 误差方程的构建
将式(10)线性化,得到双线阵相机标定参数整体解算的误差方程如式(11)所示
CΔ-L=V
(11)
式中,C为系数矩阵;Δ为标定参数的改正数;L为常数项;V为像点坐标余差。其中

(12)
在Δ中,dφ、dω、dκ为星地相机夹角系统常差修正参数,dff、dfb为相机主距改正数,dxf、dxb、dyf、dyb为相机主点改正数,dαf、dαb、dγf、dγb为线阵旋角,dβf、dβb为像点坐标的影响因子。综上,共需整体解算的双线阵相机标定参数的有15个,通过最小二乘迭代求解即可得到最优的标定参数。
3 试验与分析
3.1 试验数据与方法
本文基于宁夏数字化定标场进行相机参数标定试验,宁夏数字化定标场影像拍摄于2020年,范围大约为100 km×340 km,满足1∶2000比例尺精度要求。在宁夏定标场采集均匀分布的87个控制点作为参与在轨几何标定计算的控制数据,同时在其中某一景影像范围内选择均匀分布的40个控制点作为检查点,用于评估标定前后的定位精度。在数字化定标场影像基础上,通过同名点人工转刺的方式获取高分十四号影像(拍摄于2021年3月22日)像点坐标,像点坐标量测精度优于0.3像素。高分十四号影像覆盖及控制点、检查点分布情况如图2所示。通过87个控制点的像点坐标和地面坐标,采用在轨几何标定严密成像模型,实现双线阵相机参数整体解算,然后利用40个检查点验证标定结果的正确性。
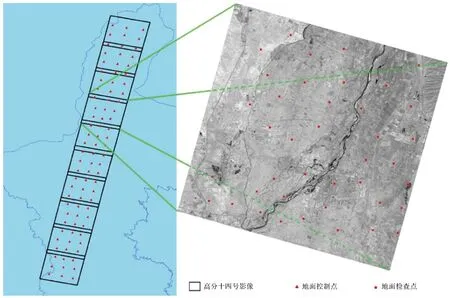
图2 高分十四号影像覆盖及控制点、检查点分布Fig.2 Image coverage of GF-14 and distribution of control points and check points
同时,为了验证远离标定场的卫星影像无控定位精度,选取2021年3月—2021年4月间拍摄的5景国外区域的高分十四号立体影像,利用影像覆盖范围内的检查点(平面高程均优于0.1 m),结合精密定姿、精密定轨和在轨几何标定参数,计算并统计无控条件下的立体影像直接前方交会定位精度,进一步分析验证几何标定结果的有效性和可靠性。
3.2 试验结果与分析
3.2.1 在轨标定试验与分析
在轨标定试验中,通过87个控制点进行了双线阵相机参数的整体解算,利用定标场内40个检查点进行了无控定位精度检测,在轨标定前后地面检查点的残差统计见表1,在轨标定后每个地面检查点的残差情况见表2,残差分布如图3所示。

表1 在轨标定前后地面检查点残差统计Tab.1 Residual statistics of ground check points before and after orbit calibration m

表2 在轨标定后每个地面检查点的残差情况Tab.2 Residual at each ground check point after orbit calibration m
由表1可以看出,在轨标定前检查点残差的均值和中误差均较大,在百米量级,标准差较小,在5 m以内,由此可知影响高分十四号卫星双线阵影像定位精度的误差主要为系统差。结合表2和图3可知,通过在轨标定,检查点残差的均值基本为零,中误差和标准差基本一致,在轨标定后检查点在平面、高程方向上的残差分布随机、无明显的系统性,表明通过双线阵相机参数的整体解算,较好地消除了影响双线阵影像定位精度的系统差。
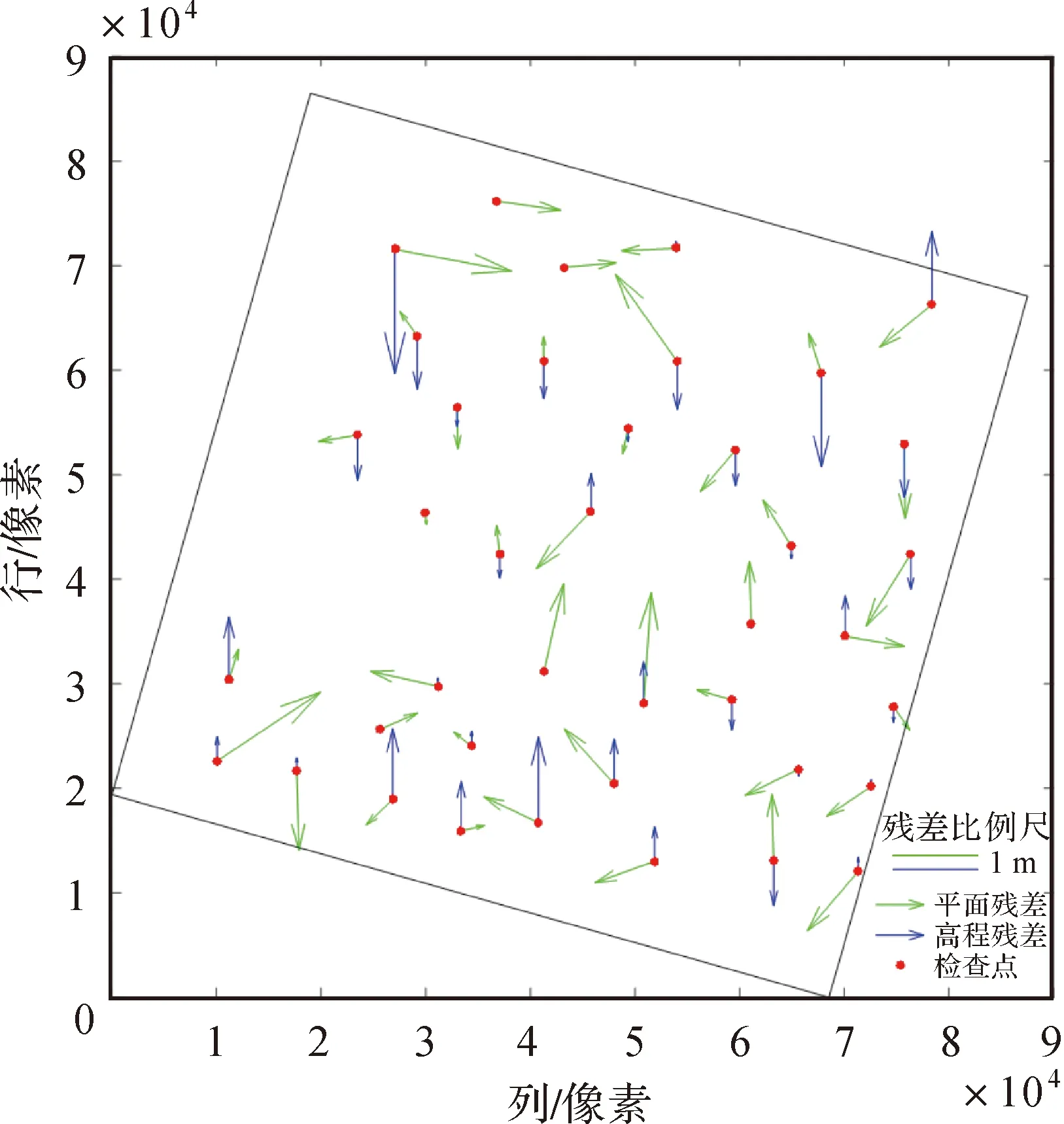
图3 在轨标定后检查点在平面、高程方向上的残差分布Fig.3 Residual distribution of check points in plane and elevation after orbit calibration
3.2.2 精度检测试验与分析
为进一步分析验证几何标定参数的有效性和可靠性,利用5个国外区域的检测场影像对上述标定结果进行无控定位精度检测,统计结果见表3。
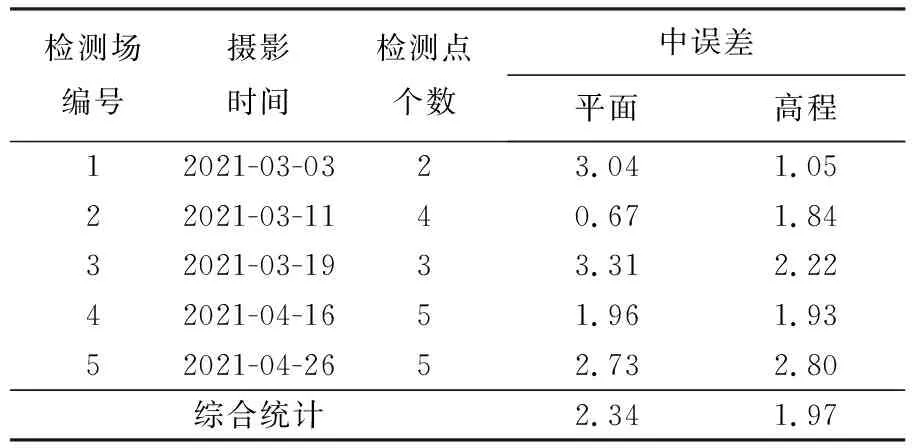
表3 国外区域无控定位精度统计Tab.3 Statistics of location accuracy without ground control points in foreign regions m
从精度统计结果来看,经过在轨几何标定后的高分十四号卫星双线阵影像直接前方交会无控定位精度达到平面2.34 m(RMS)、高程1.97 m(RMS)。该精度相较定标场平面0.76 m(RMS)、高程1.22 m(RMS)的定位精度略有下降,这主要因为在轨几何标定实际上解算的是预设模型在标定时刻的最优参数,而不同成像时刻卫星的成像系统误差会略有不同,这势必会导致在检测场使用定标场解算的标定系数时,存在一些精度损失;同时考虑到高分十四号卫星的姿态测定精度为0.3″(1σ),在500 km轨道高度上引起的平面随机误差最大为0.9 m左右,高程随机误差最大为1.8 m左右,因此该精度检测结果能够说明在轨几何标定参数的可靠性、适用性和稳定性。
4 结 语
本文在利用等效框幅思想对双线阵相机进行等效变换的基础上,构建了顾及星地相机夹角系统常差和线阵不平行性的在轨几何标定严密成像模型,利用国内定标场开展了在轨几何标定试验,利用国外检测场开展了精度检测试验。试验结果表明:双线阵相机参数整体解算较好地实现了高分十四号卫星双线阵相机高精度在轨几何标定,提升了卫星的无控定位精度。同时,在轨标定参数也具有可靠性好、稳定性强等特点。
经过在轨几何标定后的高分十四号卫星影像直接前方交会精度达到平面2.34 m(RMS)、高程1.97 m(RMS),较好地反映了在轨标定模型和算法的正确性,但这不是高分十四卫星影像最终的无控定位精度。在高分十四号卫星地面数据处理的工程实践中,为了实现更好的无控定位性能,还使用了光轴位置测量数据和激光测距数据,使得高分十四号卫星单航线无控定位精度达到国内平面1.80 m(RMS)、高程0.80 m(RMS),国外平面1.76 m(RMS)、高程0.82 m(RMS)[26]。

