顾及声速结构时域变化的海底基准站高精度定位方法

赵 爽，王振杰，聂志喜，贺凯飞，刘慧敏，孙 振

1. 中国测绘科学研究院，北京 100036； 2. 中国石油大学(华东)海洋空间与信息学院，山东 青岛 266580； 3. 中国地质调查局青岛海洋地质研究所，山东 青岛 266071

海洋空间位置信息是一切海洋活动的重要基础。作为国家重要的海洋空间信息基础设施，海底大地控制网的构建对海底基准站的定位提出了更高的要求[1-2]。目前广泛采用GNSS-Acoustic(GNSS-A)联合技术对海底基准站进行定位[3-4]。

由于海洋自然环境的广域性、复杂性和多变性，海洋信道是时变、空变、频变的复杂系统[5-6]。目前制约水下声学定位精度最为显著的要素之一是声速。国内外学者针对高精度GNSS-A定位中声速误差建模及声线跟踪改正方法做了较多研究。文献[7]顾及声速相关系统误差的相似性，采用单差、双差等组合观测值方法，削弱声速相关系统性误差影响。文献[8]基于声速垂直分层的假设，结合声线传播的层间圆弧路径，获得改进声线跟踪模型的平均声速。文献[9]顾及波束入射角，改进声线跟踪算法，实现波束角和目标坐标的迭代估计。文献[10]引入卡尔曼滤波方法对声速误差进行序贯估计。文献[11]将等效声速偏差参数化对传统交会定位平差系统扩维，采用最小二乘法将坐标参数和声速参数一并解算，但由于垂直方向的观测结构，会导致声速偏差参数与垂直方向坐标分量存在相关性，可能会降低估计的稳健性。文献[12—13]引入非参数分量表征声速系统误差，构建半参数模型进行海底点位置解算，但如果施加基于时间差分算子的强约束会引起解算结果失真。上述研究侧重考虑声速结构的空间变化，尤其是垂直方向的空间变化。此外，文献[14]提出了声速结构水平方向的梯度变化假设，在此基础上文献[15—16]从声信号传播时间天底总延迟(nadir total delay，NTD)角度进行了声速结构水平梯度建模，为海底形变监测及位移测量提供了重要思路。

除了空间变化，时域变化[17]也是声速结构的重要特点。对于声速结构时域变化的研究，通常需要大范围、高密度、高分辨率的声速剖面数据作为支撑。基于Argo浮标数据集，目前已开展了中国南海[18]、菲律宾海[19]等海域的声速结构的季节性或年际变化研究[20]，但水下定位的声呐观测时间区段远小于上述研究的时间尺度。因此，国内外学者开展了局部区域的声速场时域变化研究。文献[21]基于GNSS-A智能锚系浮标连续观测数据，对日本黑潮暖流过境区域进行了声速结构时空变化估计，从而改善海底基准站阵列平面定位精度。文献[22]基于可抛弃式温盐计数据，提出扰动声速场时域变化反演方法，提取声速结构梯度分布并分析其影响，有效提高了海底基准点的定位精度。文献[23]针对水下声学定位中声呐观测时间区间内的声速结构变化建模，提出用观测时间的二次多项式刻画扰动声速结构的时域变化，有效改善了海底点定位精度[24]。上述多项式建模方法，数学表达式简单但物理背景意义较弱，声速结构变化前后的连贯性较差。B样条函数优良的局部支撑性能够很好地适应观测数据，用样条函数的控制顶点表征非参数分量，其刻画系统误差的能力较为突出[25]，对于表达声速结构变化的光滑性有一定的优势。

本文顾及声速场时域变化以及声速结构垂直方向的变化特点，引入三次B样条函数表征扰动声速时域变化，基于声线跟踪理论，构建位置信息和声速信息迭代估计模型，进行海底基准站坐标和扰动声速的渐次修正，从而获得海底基准站的高精度位置信息。

1 声速结构时域变化影响分析

1.1 Harmonic平均声速模式

声波在海水中传播，会在介质常数不同的两个界面上产生折射，从而导致声线弯曲和传播速度发生改变，声速变化越大，弯曲越显著[4-5]。传统定位模型往往采用距离观测值[26-27]，其中距离观测值通常是由直达声信号传播时间和声速转换得到。在对定位精度要求不高的实际应用中，声速通常取调和(Harmonic)平均声速值[5]，即对垂直方向上的各处声速值进行加权平均，但平均声速通常基于深度加权计算，其值与设定的声源深度密切相关。

在高精度深海定位中若采用该平均声速模式，往往会导致定位“假点”。以典型圆走航为例，在平面方向具有良好的对称观测结构，基准站的平面定位精度较高，但垂直方向上声速误差无法被有效削弱或均衡抵消，基准站位置会因为等效平均声速的偏大或偏小而偏下或偏上(图1)，只以内符合精度作为评价指标的方法可能无法予以准确判断。制约平均声速模式下定位精度的重要原因是忽略了声速的空间变化，尤其是垂直方向的声速变化。

图1 声速变化与海底基准站垂直方向位置变化Fig.1 The variation of sound speed and the vertical locations of seafloor geodetic stations

1.2 基于离散声速剖面的声线跟踪模式

为了顾及声速结构的空间变化，在高精度水下定位测量中，通常在声呐观测的测量前、测量中、测量后采用声速剖面仪或温盐压计获取声速剖面(sound velocity profile,SVP)信息。此外，可在声呐观测的时间跨度内间歇释放多个可抛弃式温盐压计，以此加密声速结构观测。

为削弱声线弯曲误差影响，目前广泛采用基于声速剖面数据的等梯度声线跟踪方法[28-29]，即在一定的测量区域内，忽略声速结构水平空间异质性，假设海水介质垂直分层且层间声速等梯度变化，根据Snell定律，基于实测声速剖面信息进行逐层追加跟踪。但该方法的前提是认为整个或局部观测时间窗口内声速剖面结构不发生变化，但由于海洋环境的动态变化特性，显然声速剖面结构会随时间发生连续变化，在声呐观测区间采用离散声速剖面难以准确刻画声速结构时域变化特性，会导致声线跟踪所得的传播时间及据此反演得到的海底基准站坐标精度受限。

1.3 声速结构时域变化影响分析

海洋系统是由“多机理-互作用”的物理、声学、光学、化学及地质过程组成的复杂系统，其内部存在着形式多样的动力过程(如锋面、涡流与内波等)及其耦合作用，使得海洋环境产生时域与空域上的剧烈变化，因此会导致声学传播环境中，声速结构具有较为显著的空变与时变特性[30]。针对大尺度(数十甚至上百千米)研究区域，通过布设由多个矢量水听器组成的阵列接收多径声信号数据，采用海洋声学层析思想与技术[31-32]，构建时空演化四维(三维坐标加一维时间)声速场[33-34]。不同海域声速场具有不同的时空变化特性，以中国南海北部海域为例，采用经验正交函数[35]分析，声速场时域变化主要集中在水深较浅的混合层和季节性跃层，除了显著的高频特征外，具有明显的年周期变化；但深度较深的主跃层、深海等温层结构较为稳定，变化相对较小。此外，若海区内环流系统复杂多变，季风和黑潮等海洋环境影响显著，中尺度涡旋也会引起声速场发生明显的时空变化[36]。

就目前的海洋大地测量手段而言，利用直达声线对海底基准站进行定位的测量模式显然不具备上述获取多径声信号数据的条件，因而难以实现大范围声速场的时空反演。该测量模式对应的海面船走航范围一般在数千米内，小范围的声速场即声速结构，忽略中尺度(及以上尺度)物理海洋现象及其所引起的声速结构水平异质性，则主要考虑声速场时域变化引起的声速扰动。扰动声速结构主要受内波及次中尺度(空域范围是数百米到数十千米，时域范围是数天到数周)海洋动力过程影响，主要表现为持续几个小时的长周期变化和约20～60 min的短周期变化。因而，对于海底基准站高精度声学定位数据处理而言，需要关注以min及h为时域分辨率的声速结构变化特点及其影响[14,22]。

2 模型建立与解算方法

从射线声学理论出发，基于声源点与海底基准站本征直达声线模型，以声线传播时间为观测量，遵循Snell定律实施分层等梯度声线跟踪[37]，反演解算海底点坐标，其本质上依照的准则如下

|tobs-tr|=min

(1)

式中，tobs表示实际测量的声信号传播时间序列；tr表示根据射线声学原理进行声线跟踪获得的声信号传播时间序列，与声源点、海底基准站坐标及声速结构的关系如下

tr=f(Xtd,Xtp,V)

(2)

式中，f表示声线跟踪非线性映射关系；Xtd=(xtd,ytd,ztd)表示声源点三维坐标；Xtp=(xtp,ytp,ztp)表示海底基准站三维坐标；V表示声速结构。

构建基于稳健贝叶斯最小二乘的“分步迭代-渐次修正”反演模型，如图2所示，即“固定声速-求解位置”与“固定位置-估计声速”交替迭代进行，对海底站坐标和声速结构渐次修正，直至解算结果满足阈值要求，从而求得海底基准站位置和声速结构时域变化。

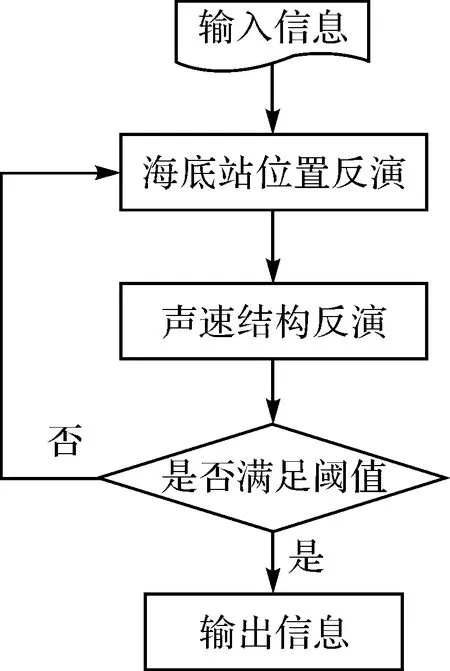
图2 “分步迭代-渐次修正”反演模型Fig.2 The inversion model of “stepwise iteration & progressive corrections”

具体模型建立与解算方法如下：

(1) 海底站位置反演。海底基准站位置反演主要是采用“固定声速-求解位置”进行。根据泰勒级数线性化原理，将声线跟踪非线性化系统在海底基准站概略坐标处进行线性化，可得式(3)

tr=f0+A1·dXtp

(3)

其中，关于平面位置的求导可按照式(4)基于射线声学基本原理求得，关于z方向的求导可由数值分析方法求得[38]

(4)

基于稳健贝叶斯最小二乘估计原理[40]，海底基准站位置改正数解算得

(5)

(2) 声速结构反演。声速结构反演主要是采用“固定位置-求解声速”。实际声速结构是参考(背景)声速结构与扰动声速结构的耦合。考虑声速场时域变化，可将声速结构表达如下

V(z,te)=Vr(z)+Vp(z,te)

(6)

Vp(z,te)=a0+a1(te-t0)+a2(te-t0)2

(7)

式中，te为观测时刻；ai(i=0,1,2)为模型参数；t0为参考时刻。该方法中离散观测时刻对应的声速结构之间没有关联性，故声速结构变化的光滑性降低。需要指出的是，考虑到水声定位作业时间、空间范围，声速剖面变化主要受内波和次中尺度海洋动力过程影响，因而窗口设置可分步进行，即先设置较大窗口，后设置较小窗口，依次对长、短周期扰动声速进行修正。

本文顾及广泛意义上的声速结构时域连续变化的特点，引入三次B样条函数[24]进行声速结构变化拟合。此外，本文顾及海水上下层声速结构变化差异，即考虑到在声呐观测时间窗口内深水层声速变化平稳且微弱的特点，将扰动声速根据经验深度设置为分段函数形式。将整个观测时刻序列按照一定时间间隔Δt划分为m段。若观测时刻te属于第i段，则其扰动声速结构如下

(8)

式中，a表示B样条函数系数；B表示B样条基函数；d表示B样条次数，本文取d=3；z0表示参考深度，对于深水海域一般经验取值为1000～1600 m；ui为单位化观测时刻，计算公式为ui=(te-ti)/Δt，Δt=ti+1-ti。ti、ti+1分别为第i段的始、末观测时刻，i=1,2,…,m。

与“固定声速-求解位置”同理，将声线跟踪非线性化系统基于参考声速剖面进行线性化，可得

tr=f0+A2·da

(9)

(10)

同理，基于稳健贝叶斯最小二乘估计原理，可实现声速结构时域变化反演。需要指出的是，有多个时间窗口进行解算时，可通过循环完成多窗口的声速结构反演。

反演得到的声速结构变化量被反馈应用到海底基准站坐标计算中，重新进行海底基准站位置反演，直至坐标增量及声速变化量均在预设的阈值范围内结束解算，至此完成了海底基准站坐标和扰动声速的渐次修正。

3 算例分析

算例采用2019年7月南海“海洋大地测量基准与海洋导航新技术深海综合试验”实测数据进行分析。试验区域平均水深约3000 m，测量船搭载GNSS接收机、高精度姿态传感器、声速剖面仪和海面长基线水声定位系统等设备。试验采用往返多折线走航策略，对海底基准站实施连续观测，采集声呐测时数据、声速剖面数据、GNSS数据、姿态数据及其他传感器数据。测量船航迹、海底基准站位置及声速剖面测量(后3次测量)概略位置如图3所示。

图3 测线航迹及海底应答器位置Fig.3 The surveying tracks and the seafloor transponder

自2019年7月13日至7月15日，在走航声呐观测期间采用声速剖面仪共进行4次声速剖面测量，自上而下与自下而上(以转折时刻划分)按照1 s采样率进行声速相关要素(温度、压力等)测量，共获得8个声速剖面记录，其观测时间区间及对应SVP编号见表1，其中记录时间为北京时间。声速剖面仪测量范围为1400～1550 m/s，声速测量分辨力为0.015 m/s，声速测量精度优于0.06 m/s。

表1 不同SVP观测时间区间统计Tab.1 The observation epochs for different SVPs

对上述8条SVP记录文件进行数据预处理，主要包括声速测量野值剔除、部分声速剖面数据延拓以及相邻同梯度声速层合并。计算平均声速剖面以及各声速剖面与平均声速剖面的差值，如图4所示，该深海典型声速剖面由温度垂直分布的混合层、跃变层和深海等温层的3层结构所构成。海洋表面受阳光照射及风雨搅拌等作用，海洋表面混合层的声速变化最为显著，最大变化幅度可达6.88 m/s，主跃变层的声速变化相对较为稳定，波动幅度不大于1.38 m/s，深海等温层的声速变化最为平缓，一般小于0.23 m/s。鉴于声速剖面仪的测量精度和实际测量声速剖面间变化幅值，暂不考虑声速结构异质性，声速结构时变特性是客观存在。

图4 平均声速剖面及声速变化值Fig.4 The average sound speed profile and the variation of sound speed

为了评价声速时变误差，固定海面声源点和海底基准站位置，分别采用不同SVP进行声线跟踪获得传播时间并进行对比。设置水深为3000 m，按照往返多折线走航观测策略，海底基准站坐标设置为(0,0,-3000)，海面声源点1和声源点2坐标分别设置为(-4500,0,-5)、(-3000,0,-5)，如图5所示。

图5 海面声源点与海底基准站相对位置Fig.5 The sea-surface sound sources and the seafloor geodetic station

采用系列SVP数据，固定海底基准站，分别固定声源点1和声源点2进行声线跟踪，所得声线入射角和声信号传播时间如图6所示。基于8个不同观测时刻获得的声速剖面进行声线跟踪，声源点1对应的声线入射角波动范围为57°9′14.916″～57°11′24.336″，幅值为2′9.420″，跟踪时间波动范围为3 616.41～3 619.74 ms，幅值为3.33 ms；声源点2对应的声线入射角波动范围为45°35′21.006″～45°38′11.088″，幅值为2′50.082″，跟踪时间波动范围为2 836.13～2 838.93 ms，幅值为2.80 ms，上述时间变化幅值远大于海试典型声呐设备测时精度(40 μs)。

由图6可知，在固定海面声源点和海底基准站的前提下进行声线跟踪时，采用不同观测时刻的声速剖面，跟踪所得的声线角和传播时间均有所不同，并且随航迹变化，远离海底基准站的声源点基于不同SVP所得的跟踪传播时间差异更大，这主要是由声速结构的时域变化引起的。因此，在水下声学定位中，尤其是基于声线跟踪算法进行的高精度水下定位，需要顾及声速结构的时域变化，即在海底基准站坐标反演的总过程中，声速结构变化的反演是不可或缺的一部分。

图6 基于不同SVP进行声线跟踪所得的声线入射角及传播时间Fig.6 The ray-tracing incident angles and travelling time based on different SVPs

区别于只进行海底基准站位置反演的传统方法，本文分别采用二次多项式法(quadratic polynomial,QP)和三次B样条函数法(cubic B spline,CBS)进行扰动声速结构反演。基于“分步迭代-渐次修正”反演模型，分别采用QP法进行首次修正和二次修正的声速变化值，如图7所示，其中声速修正1表示基于长周期窗口的声速改正，声速修正2表示基于短周期窗口的声速改正。由于多项式拟合方法主要是表达声速结构变化与观测时间的函数关系，因此窗口间的声速变化存在明显不连续性，即间跃点，这与实际声速变化规律不相符，因而可能会导致扰动声速结构反演结果可能与真实情况存在不可忽略的差异。此外，如果声速结构在涡流等特殊区域发生突变，QP法在预设的声呐观测时间窗口内进行声速修正值反演，窗口内出现的异常值会导致该区间所有修正值受到影响。但CBS法基于长短周期耦合效果进行修正，由于B样条良好的局部支撑性，声速突变异常值会作用在节点控制范围内，即对某段函数的改动不会产生全局性的系数调整。

图7 基于二次多项式法的声速修正Fig.7 The corrections of sound speed based on the quadratic polynomial method

采用CBS法进行首次修正和二次修正的声速变化值，如图8所示。顾及三次B样条函数进行拟合的分辨率在于节点区间，因而CBS法基于长短周期的耦合结果进行声速结构变化的反演。同QP法，由于初始声速设置存在较大偏差，首次声速修正值较大，最大值可达1.59 m/s；二次修正值小于0.2 m/s。三次B样条函数具有较好的局部支撑性，在表征声速结构连续、缓慢变化的特点方面具有优势，因而其细节刻画能力更强，反演的声速结构变化的连续性和稳定性较QP法更好。

图8 基于三次B样条函数法的声速修正Fig.8 The corrections of sound speed based on the cubic B spline method

经过海底基准站位置和扰动声速结构迭代反演，实现了海底基准站坐标和声速结构的渐次修正，最终的定位计算结果见表2。是否施加声速修正，海底基准站垂直方向坐标变化较为明显；且只有施加准确合适的声速修正，才能不引起平面方向定位精度恶化。因为声速修正不合理，会使得径向测时误差在平面方向的分量或投影不能均衡或抵偿。不加修正地只反演海底基准站坐标的方法，海底基准站三维坐标内符合精度优于10 cm，声呐测时观测值所对应的单位权中误差为1.42 ms，基于QP法和CBS法进行声速修正方法对声速结构变化进行反演，其对应的单位权中误差分别为0.38、0.18 ms，海底站三维坐标的内符合精度优于5 cm。

表2 不施加/施加声速修正的海底站位置解算结果Tab.2 The positioning results of the seafloor station without/with the sound speed corrections

统计传统方法(不施加声速修正)、QP声速修正法、CBS声速修正法的观测值残差值，如图9所示。不施加声速修正时，残差中包含了由于声速场时域、空域变化等综合因素耦合的系统性偏差，呈现出明显的“锯齿”状，残差值波动范围为-3.50～3.50 ms。经QP声速修正后，较为显著的系统性误差被消除，残差值起伏明显缓和，其波动范围为-1.50～1.50 ms。采用CBS声速修正后，残余误差中系统性误差显著消除，呈现出随机特点，残差值变化范围为-0.60～0.60 ms。

图9 3种方法的声呐测时观测值残差Fig.9 The residuals of acoustic timing observations based on three methods

采用3种方法(传统法、QP声速修正法、CBS声速修正法)进行海底基准站定位解算，声呐测时观测值残差的统计特征(最大值(Max)、均值(Mean)、标准差(Std)、均方根误差(RMS))见表3。从残差绝对值的均值来看，传统法为1.22 ms，QP法为0.36 ms，CBS法为0.17 ms；从残差的均方根误差角度看，传统法、QP法、CBS法分别为1.43、0.44和0.21 ms。不施加声速修正的反演模型，即没有顾及声速剖面的时域变化性质，而将声速误差作为制约水下声学定位最重要的要素，对其时变特性的忽略势必会弱化定位结果的精度及可靠性。反之，施加了声速修正的反演模型下，残差的均方根误差值明显变小；QP方法作为插值或拟合中最简单的工具或方法，但基于不同窗口划分进行长、短周期的声速修正，在各窗口节点处不可导，不具有光滑性，与广义上的声速时域变化的连续性有所分歧。较QP声速修正法而言，CBS方法是基于离散声速剖面，由已知的观测数据为未知声速信息建立一个简单、连续的解析模型，并据此模型进行非观测声速信息特性的推测。CBS声速修正法采用的样条函数具有更好的光滑性和连续性，更符合声速结构变化的平稳、连续的实际特点，因而获得了更好的定位效果。

表3 不施加/施加声速修正的观测值残差统计结果Tab.3 The observation residuals without/with the sound speed corrections ms

4 结 论

本文在对声速结构时域变化影响分析的基础上，给出了一种顾及声速结构时域变化的海底基准站高精度定位方法，即“分步迭代-渐次修正”的位置信息和声速信息迭代反演方法，进行海底基准站坐标和扰动声速的渐次修正，通过实测数据验证得到以下结论：

(1) 通过基于8个不同采样时间的声速剖面进行同点跟踪，所获得的声线传播时间具有毫秒量级的差异，这表明在高精度海底基准站定位中采用声线跟踪方法时声速结构时域变化不可忽略。

(2) 施加声速修正的反演模型，有效消除了声速结构变化引起的声速相关系统性误差，传统不施加声速修正的观测值残差均方根误差大于1 ms，施加声速修正的反演模型对应的观测值残差均方根误差小于0.50 ms。

(3) 三次B样条函数具有良好的局部支撑性，较多项式方法具有更强的扰动声速细节刻画能力，两者修正方法对应的观测值残差均方根误差分别为0.44和0.21 ms，定位解算验后单位权中误差分别为0.38和0.18 ms，有效提高了海底基准站定位精度。

需要指出的是，本文忽略了声速场的水平异质性，后期需要结合地区洋流等物理海洋数据进行深入分析，构建更为完备的顾及声速场时-空变化的海底基准站高精度定位方法。

致谢：特别感谢国家重点研发计划“海洋大地测量基准与海洋导航新技术”项目组及深海试验全体科研人员的合作与支持。