两体系统量子相干性的动力学和守恒
高德营,李宁
(聊城大学东昌学院,山东 聊城 252000)
0 引言
量子关联(量子纠缠和量子失协)和量子相干性是量子理论中的两个基本概念[1]。量子关联表示两体或多体系统的量子特性,量子相干性刻画了叠加态呈现的量子干涉能力。它们是不同的物理概念,但有着密切的联系,量子相干性是量子关联、量子相变[2,3]、量子干涉[4,5]等非经典效应存在的前提条件。自从把量子相干性作为一种资源,并建立它满足的理论框架,度量量子相干性的方法相继被提出,例如l1-norm相干性度量[6]、相对熵相干性度量[6]、几何相干性度量[7]、coherence of formation[8]等,对量子相干性的研究成为一个热点,研究人员从各个方面对它进行了研究[9],其中一个方面是开放系统中量子相干性的动力学演化[10-13]。考虑到系统与环境不可避免的非平衡耗散的退相干过程,研究开放系统量子相干性的动力学特征变得尤为重要。
对于一个复合量子系统,例如一个双Jaynes-Cumming型系统,在各子系统的量子纠缠和量子失协的动力学演化中,它们满足一定的守恒关系式。文献[14]考虑空间独立的两个系统组成的一个无耗散复合系统,给出了子系统的量子纠缠满足的守恒关系式;文献[15]讨论了一个无耗散系统中偶极相互作用对量子失协和量子纠缠满足的守恒关系式的影响,发现量子纠缠和量子失协满足的守恒关系式并不相同。与量子纠缠和量子失协一样可以作为量子信息资源的量子相干性,在一个有耗散的复合系统中所满足的守恒关系式还未见研究报道。
本文主要研究了两个空间独立的原子-零温真空库组成的复合系统,以及各子系统的量子纠缠和量子相干性动力学演化特性。给出了各子系统的量子纠缠和量子相干性满足的守恒式,并讨论了影响守恒式的因素。发现初始类贝尔态和初始态的纯度决定了各子系统的量子纠缠和量子相干性满足不同的守恒式。对于同一类贝尔态,子系统量子纠缠和量子相干性的守恒式不受马尔科夫环境或者非马尔科夫环境的影响。
1 物理模型
考虑两个二能级原子分别与两个独立零温真空库的相互耦合,由于两个单原子-库之间没有相互作用,所以先考虑单原子-库的耦合,然后把结果推广到两个原子-库的情形[16,17]。



2 量子相干性和量子纠缠的计算


3 结果与讨论
根据前面的分析,考虑非马尔科夫和马尔科夫环境两种情况,分别讨论复合系统各个子系统的量子纠缠和量子相干性的动力学演化,并就各子系统量子纠缠和量子相干性满足的守恒关系进行研究。
图1、图2分别表示非马尔科夫环境下两原子的量子纠缠和量子相干性随时间Rt和参数θ的变化。由图可见,两原子的量子纠缠出现了纠缠死亡和恢复现象,而两原子的量子相干性没有出现。进一步,两原子的量子相干性随着两原子初始状态的不同而演化的动力学不同,在实际应用时,可以选择合适的两原子的初始状态,以获得相应的相干性。出现这种现象的物理机制为:这里所考虑的洛伦兹谱密度相当于有衰减的Jaynes-Cumming模型[19],量子纠缠不会长时间保留,出现了衰减,针对某些初始纠缠态,系统纠缠在动力学过程中甚至会出现突然死亡,但停一段时间纠缠又恢复,是非马尔科夫效应的记忆效应,流向环境的能量或者信息部分地反馈到量子系统。而量子相干性是系统密度矩阵非对角项的绝对值和,量子系统与环境相互作用中,非对角项在演化过程中不会在一定时间内消失,仅在某时刻上衰减为0,受环境非马尔科夫效应的影响,表现为随着时间振荡的现象。
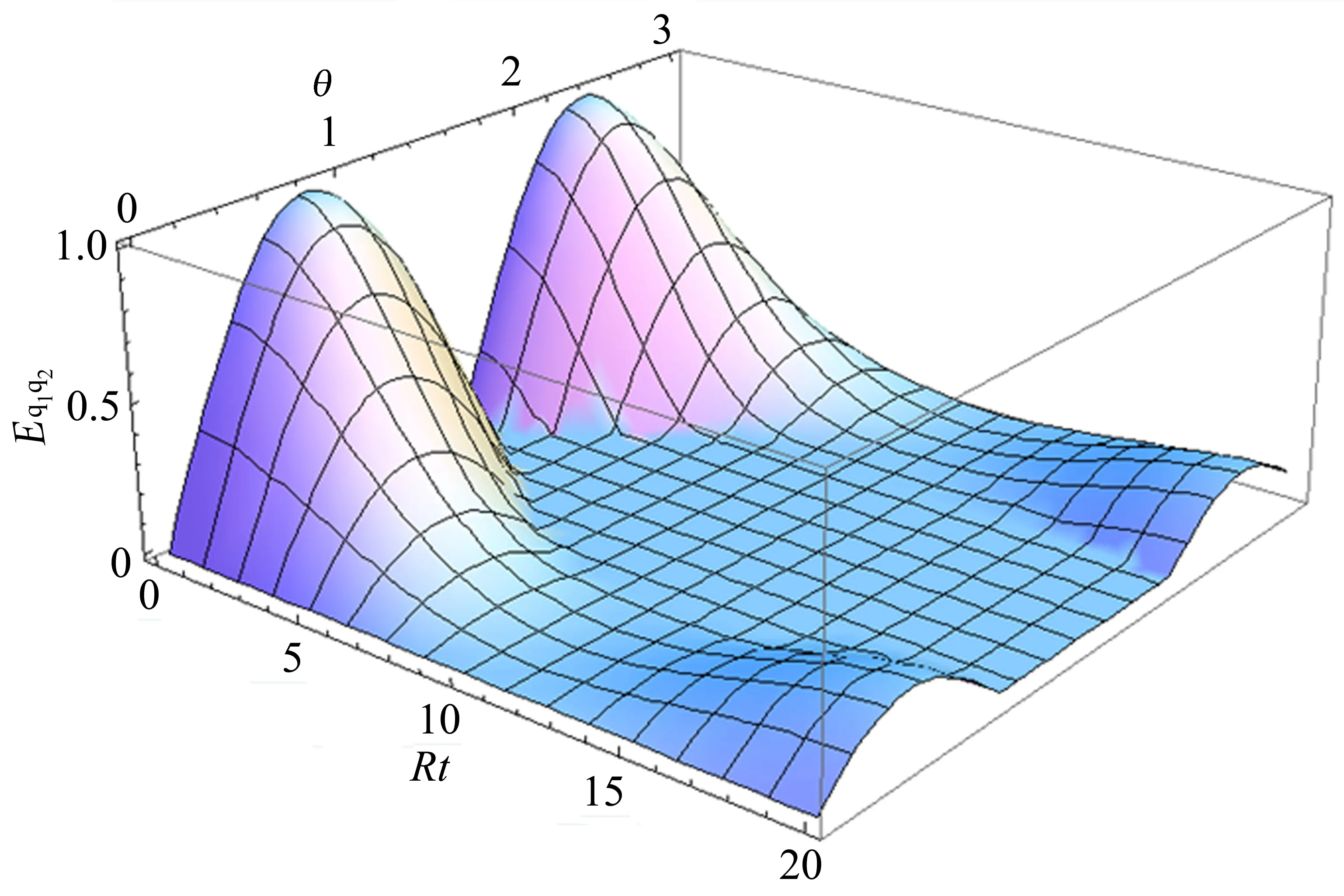
图1 两原子的量子纠缠Eq1q2随着无量纲时间Rt、参数θ的变化,r=1,λ=0.05 RFig.1 Dimensionless time evolution of quantum entanglement Eq1q2between the two atom for the parameter θ with pure Bell-like states as initial states(r=1)in the non-Markovian regime(λ=0.05R)

图2 两原子的量子相干Cq1q2随着无量纲时间Rt、参数θ的变化,r=1,λ=0.05RFig.2 Dimensionless time evolution of quantum coherence Cq1q2between the two atom for the parameter θ with pure Bell-like states as initial states(r=1)in the non-Markovian regime(λ=0.05R)
图3、图4分别表示非马尔科夫环境下两原子的量子纠缠和量子相干性随时间Rt和初始态纯度r的变化。当r较小时两原子没有纠缠,而量子相干性总是存在的;随着r的增加,两原子的量子纠缠出现了纠缠死亡和恢复现象,而两原子的量子相干性没有出现类似的现象。对此现象的解释是:改变态的纯度r,也就是改变两原子的初始态,当纯度取值较小时两原子没有初始纠缠,自然不会出现纠缠的动力学演化。随着纯度的增大,两原子有了初始纠缠,由于耗散环境以及非马尔科夫效应的作用,出现了纠缠死亡和恢复现象,而量子相干性因相互作用过程中非对角项不会消失而始终存在。

图3 两原子的量子纠缠Eq1q2随着无量纲时间Rt、参数r的变化,θ=π/8,λ=0.05RFig.3 Dimensionless time evolution of quantum entanglement Eq1q2as a function of paramete r with θ= π/8 and λ =0.05R
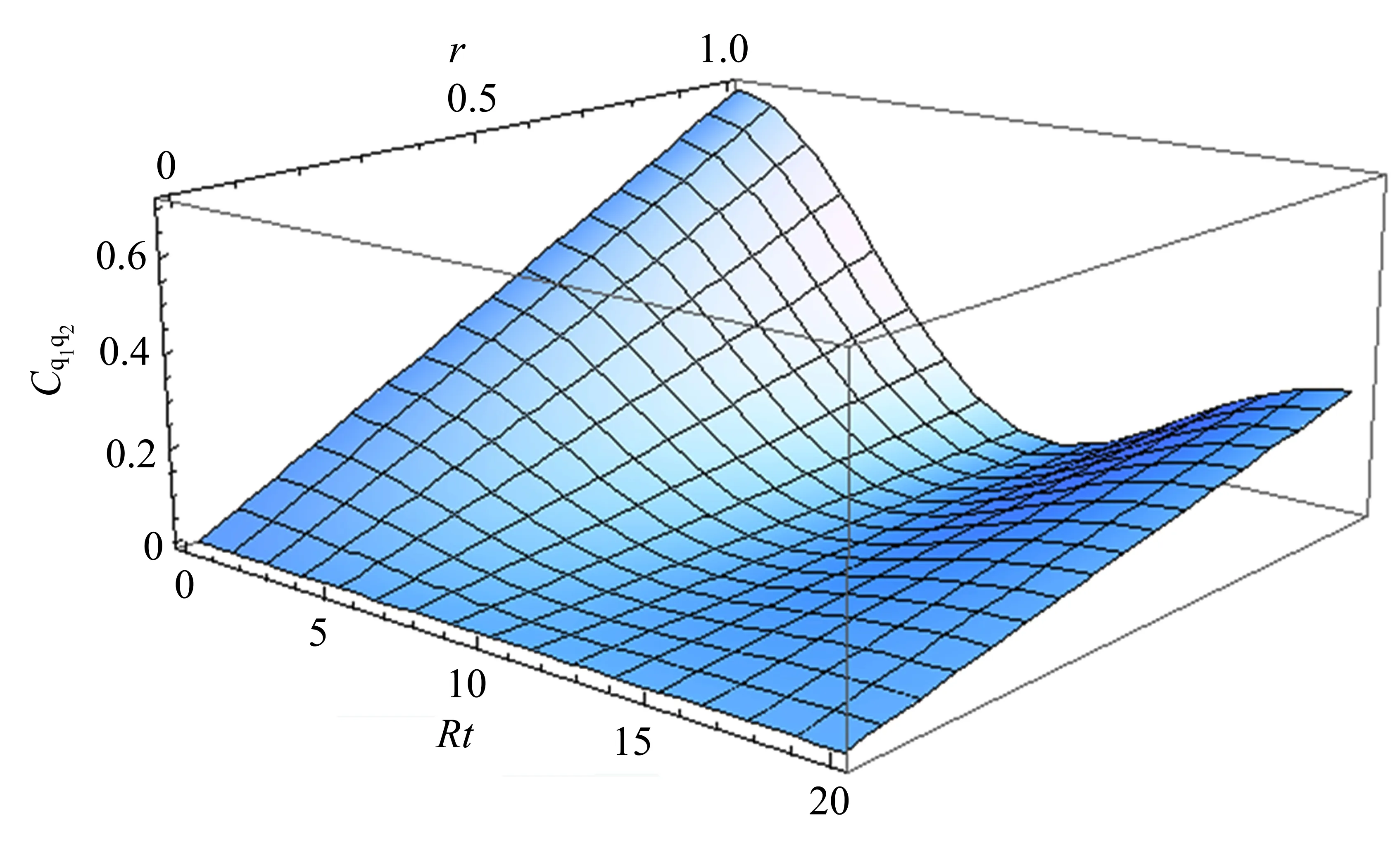
图4 两原子的量子相干性Cq1q2随着无量纲时间Rt、参数r的变化,θ=π/8,λ=0.05RFig.4 Dimensionless time evolution of quantum coherence Cq1q2as a function of paramete r with θ= π/8 and λ =0.05R
图5、图6表示非马尔科夫环境下,纯度r=1、r=0.8两种情况下的两原子q1⊗q2、两库r1⊗r2,及其他子系统q1⊗r2、q2⊗r1、q1⊗r1、q2⊗r2量子相干性的动力学演化。可以看到两原子量子相干性Cq1q2的演化表现为典型的非马科夫性特征,随着时间的增加其数值逐渐减小为0。与两原子的量子相干性相反,两库的量子相干性Cr1r2从0开始增加,最终为一定值,通过计算发现两原子量子相干性和两库量子相干性的代数和保持不变,满足关系式Cq1q2+Cr1r2=|sin2θ|,表明两原子的量子相干性并没有消失,而是转移到了两库,它们互为补充,其代数和为初始两原子的相干性|sin2θ|。对于复合系统中各子系统量子相干性的演化进行进一步研究,发现它们满足守恒关系式和Cq1q2+Cr1r2+2Cq1r1|cotθ|-2Cq1r2=|sin2θ|,表明在复合系统中,各子系统量子相干性并没有消失,而是发生了转移,并且满足某一守恒关系式。对于此复合系统各子系统量子纠缠的动力学演化,通过计算发现仅当 |sinθ|< |cosθ|时,量子纠缠满足守恒式 Eq1q2+Er1r2+2Eq1r1|cotθ|-2Eq1r2=|sin2θ|。需要指出的是,文献[25]研究了量子纠缠满足的守恒式,指出在两个耗散量子系统组成的复合系统中,量子纠缠可以在各个子系统中稳定地分布,并满足一个没有约束条件且并不依赖于库场具体形式的守恒式Qq1q2+Qr1r2+2Qq1r1|cotθ|-2Qq1r2=|sin2θ|,守恒式中Q为共生纠缠E=max{0,Q}中的一个变量,它可能是一个正数,也可能为一个负数。计算表明此处所得的纠缠守恒式虽有约束条件|sinθ|<|cosθ|,而文献[25]中没有约束条件,但结论是一样的,表示了复合系统中子系统的纠缠具有稳定分布的特征。通过上面的讨论发现各子系统之间的量子相干性满足更多的守恒式,相对于量子纠缠,量子相干性是一种更为基本的量子资源。
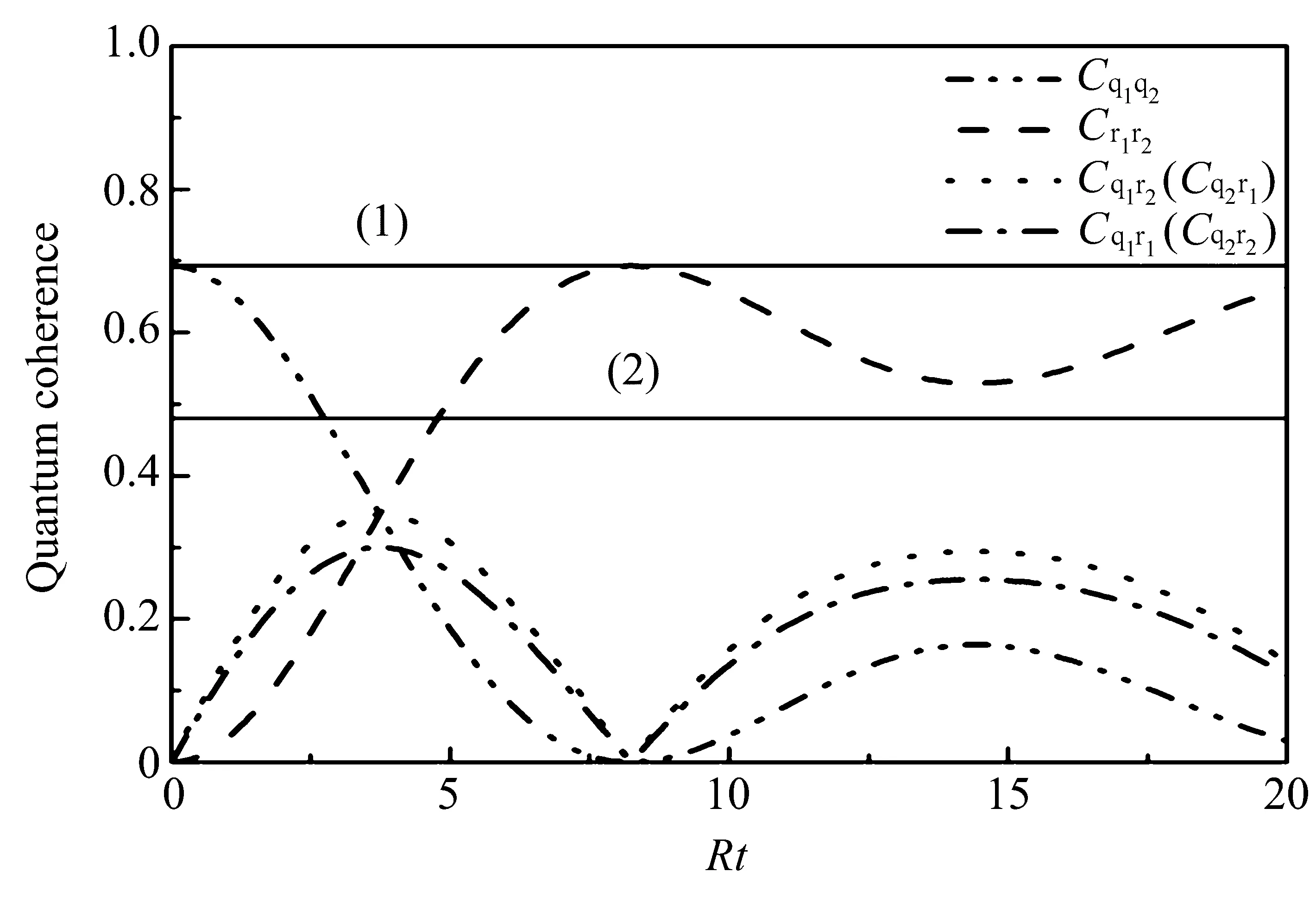
图6 子系统的量子相干性随无量纲时间Rt的变化,实线(1)和(2)表示量子相干不变量Cq1q2+Cr1r2,+++,r=0.8,θ= π/6,λ=0.1RFig.6 Quantum coherence for different partitions as a function of Rt with r=0.8,θ= π/6 in the non-Markovian regime(λ=0.1R).The solid line(1)and(2)denote the coherence invariants of Cq1q2+Cr1r2,+++
以上复合系统中各子系统的量子相干性和量子纠缠满足守恒式的讨论基于两原子的初态为类贝尔态,即r=1时。若改变两原子的纯度,即改变r的取值,守恒关系式会发生变化吗?通过计算表明当0<r<1时,子系统的量子纠缠不满足类似的守恒式。但子系统的量子相干性满足两个类似的守恒式,分别为,图6中的实线(1)和(2)表示这两个守恒式。相对于量子纠缠,各子系统的量子相干性满足更多的守恒关系式,是因为量子纠缠出现了突然死亡和突然恢复现象,而量子相干性没有这样的特性。
图7表示马尔科夫环境下各子系统量子相干性的动力学演化。由图可见,两原子量子相干性Cq1q2从最初的最大值减小到0,表现为马尔科夫特性。两库之间的量子相干性从0增加到最大值。计算表明,对于马尔科夫环境下,虽然各子系统量子相干性的动力学演化不同于非马尔科夫环境,但量子相干性守恒式是一样的。这表明子系统量子相干性守恒式与所处的环境没有关系。计算表明马尔科夫环境下量子纠缠满足的守恒关系与非马尔科夫环境下满足的关系也相同。对此现象的理论解释为:当原子与库相互作用,洛伦兹谱宽度λ与原子激发态的衰减系数R相对取值不同时,系统会出现非马尔科夫过程和马尔科夫过程,各子系统动力学演化的机理不同,进而具体的演化过程不同,但无论哪一个过程量子纠缠都不会消失,而是在各子系统之间转移。
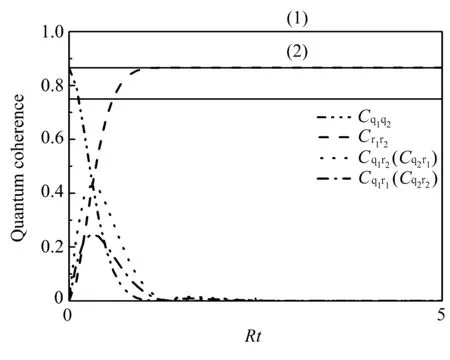
图7 子系统的量子相干性随无量纲时间Rt的变化,实线(1)和(2)表示量子相干不变量+Cr1r2,+++,r=1,θ= π/6,λ=5RFig.7 Quantum coherence for different partitions as a function of Rt with r=1,θ= π/6 in the Markovian regime(λ =5R).The solid line(1)and(2)denotes the coherence invariants of Cq1q2+Cr1r2,+++
4 结论
从单个原子与零温真空库的耦合,推广到两个相互独立的原子-库的相互作用。研究了此复合系统中各子系统量子纠缠和量子相干性的动力学,并讨论了各子系统的量子相干性和量子纠缠的守恒关系式。结果表明:各子系统的量子相干性不会像量子纠缠那样出现突然死亡和恢复现象,其动力学演化受初始态和纯度的影响。通过对子系统量子相干性的研究,发现量子相干性并没有消失,而是在子系统之间相互转移,满足相干守恒式。满足的相干守恒式不受两原子初始态ρΦ(0)、ρΨ(0)的影响,也不受非马尔科夫环境或者马尔科夫环境的影响,但受初始态纯度的影响。子系统的量子纠缠因为出现突然死亡、过了一段时间又恢复这一现象,满足的守恒式不同于相干性的。这一点表明量子相干性是一种比量子纠缠更为基本的量子资源。所进行研究可以加深对量子相干性和量子纠缠的认识,对于量子信息处理具有一定意义。

