两模机械系统中振动模式参量耦合强度调控的实验研究
袁泉,龚志成, 毛添华,谌成渝, 付号,3*
(1中国科学院精密测量科学与技术创新研究院波谱与原子分子物理国家重点实验室,湖北 武汉 430071;2中国科学院大学,北京 100049;3中国工程物理研究院研究生院,北京 100193)
0 引言
机械振子可以与多种物理场作用,将其转换为振子上的振动[1-4]。利用机械振子耦合多个物理系统,通过相干操控振动在机械振子上的传递,可以构造出用于实现不同物理系统之间信息处理的器件[5-7]。人们在机械振子的相干操控方面已经开展了大量的实验研究,借鉴量子系统中操控量子态的方法,目前已经提出了许多机械振子上的相干操控方案[7-9]。例如,在两模机械系统中,已经通过类拉比振荡、类朗道齐纳隧穿的操控方法,在两模机械系统中实现了振动在振子上的非绝热传递[10,11]。此外,人们还演示了拓扑操控[12]、几何相位操控[13]等具有高鲁棒性的操控方案。
振动在机械振子上的相干传递需要实现振动模式间的可控耦合。其中,在耦合机械振子系统中,通过对模式的振动频率进行周期性调制来施加参量驱动场,当驱动频率等于模式间的频率差时,两模式被共振耦合起来,并且可以通过控制驱动场强度实现对振子间的耦合强度有效调控,因此这种通过施加参量驱动耦合两模式的方法在各种微纳机械振子器件中都有着广泛的应用[8,14,15]。例如,通过将不同振动模式与光场、电磁场等作用,已经在诸如石墨烯鼓、微悬臂阵列、薄膜等不同结构的机械振子中利用参量驱动的方法实现了振动模式间的可控耦合[15-19],并实现了逻辑门[20]、路由器[21,22]、非互易性器件[23]等具有不同功能的信号处理器件。但是,研究表明模式间的参量耦合强度不仅与驱动的强度有关,同时还受到模式间频率差等因素的影响。由于受微纳加工工艺和材料力学性能等诸多因素的影响,机械振子频率上的差异在实验上普遍存在,因此研究模式频率差与模式耦合强度之间的关系对于微纳机械振子器件的相干控制具有重要意义。
本文在基于两根耦合悬臂梁的两模机械系统中研究了模式频率差对模式耦合强度的影响。利用激光囚禁其中一根悬臂梁,通过调制囚禁光功率施加参量驱动,实现了振动模式间的参量耦合,进一步开展了不同模式频率差下模式参量耦合的实验,研究了模式频率差与模式耦合强度之间的关系,并利用这一关系演示了一种测量振子间相互作用强度的方法。
1 实验装置
实验中所使用的机械振子是两根连接在同一基底上的悬臂梁。两根梁的厚度和宽度相同,分别为10 μm和200 nm,但是长度有所差异,其中一根(梁1)为200 μm,另一根(梁2)为180 μm。悬臂梁的基底连接着一个三维压电陶瓷位移器(PZT),用来调节悬臂梁的空间位置,使梁1位于由两个光纤端面所构成的法布里-珀罗腔中。整个装置放置在一个真空度高于10-6Pa的真空腔内,以减少空气阻尼对振子振动的影响。用一束1550 nm的激光实现对梁1的光学囚禁,激光功率由电光调制器(EOM)进行含时调制,调制信号由任意波形发生器(AWG)产生。调制后的1550 nm激光通过一个10 dB的分束器(BS1)进行分束,其中10%的光由光电探测器(PD)收集,用于对1550 nm激光功率进行实时监视。其余的光和另外一束1533 nm探测光通过一个3 dB的分束器(BS2)混合后一并输入到光腔中。为了减小探测光对悬臂梁振动的影响,输入到光腔中的1533 nm激光功率仅为10 μW。反射光经过一个光学循环器(OC)后,利用带通滤波器(BF)使得只有1533 nm的激光能够被光电探测器收集,用于测量悬臂梁的振动,并利用电子频谱仪(ESA)在频域上对悬臂梁振动进行分析。
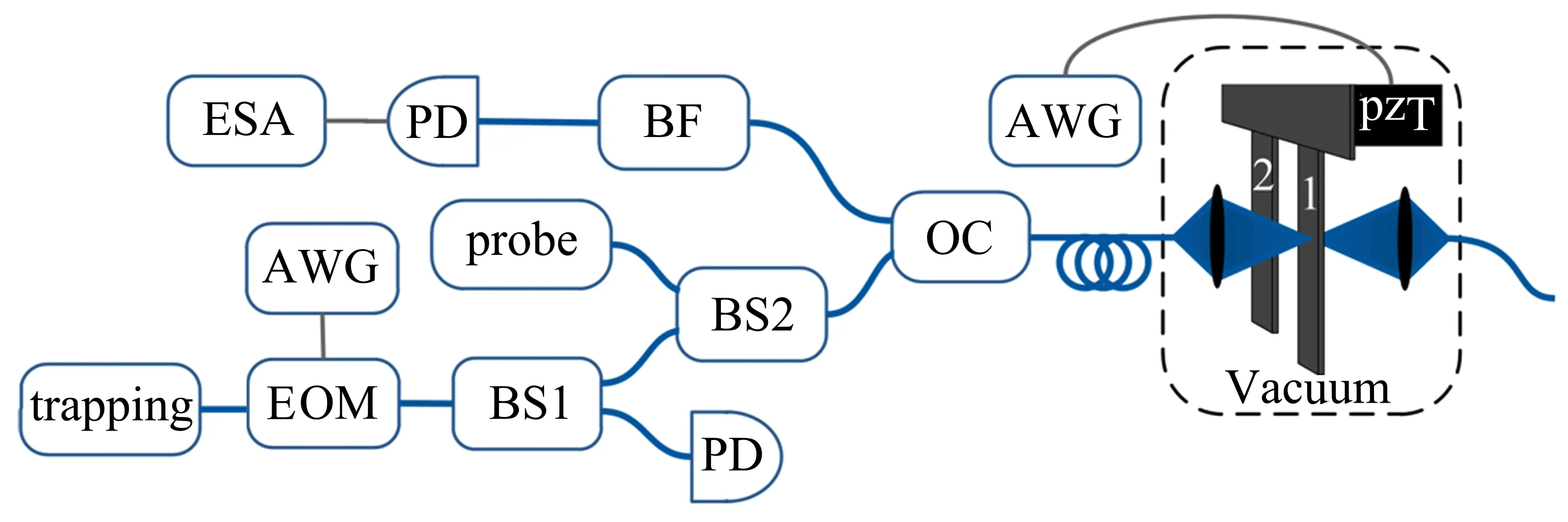
图1 实验装置示意图Fig.1 Schematic diagram of the experimental setup
2 实验结果与讨论
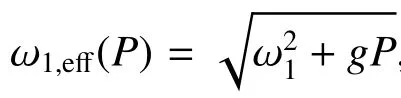
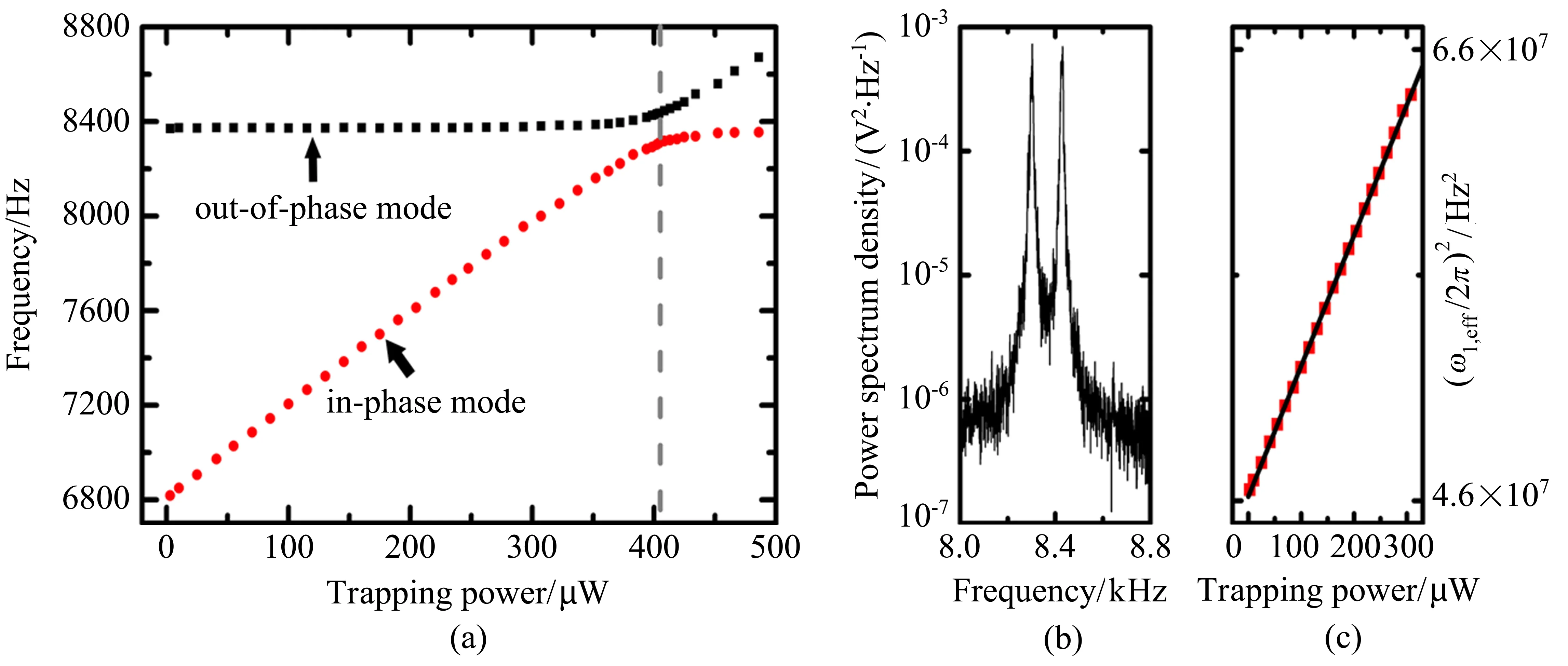
图2 (a)不同囚禁光功率下同相模和反相模的振动频率;(b)囚禁光功率P=404 μW处振子的热振动功率谱;(c)囚禁光功率在0~308 μW范围内及其线性拟合结果Fig.2 (a)Frequencies of out-of-phase mode and in-phase mode for different trapping laser power;(b)The thermal oscillation power spectral at trapping power of P=404 μW;(c) for different trapping laser power from 0 to 308 μW with the linear fitting result
通过对囚禁光功率的周期性调制来施加参量驱动,可以实现两振动模式间的共振参量耦合。实验中对囚禁光功率进行周期性调制P(t)=P0+Pdcos(ωdt)施加参量驱动,当驱动频率ωd与模式频率差δω相同时,两个模式被共振耦合起来。在囚禁光功率P0=308 μW时,通过施加频率为ωd/2π=δω/2π=381 Hz的参量驱动,研究了驱动强度Pd与模式耦合强度的关系,如图3(a)所示。可以看到,随着Pd的增大,同相振动模式的共振峰在逐渐展宽。进一步增大Pd,当Pd=28 μW时,在同相振动模式上观察到正交模式劈裂,此时两模式被有效地耦合起来,正交模式劈裂即为模式间的参量耦合强度,这一现象类似量子系统中的拉比劈裂现象[26]。实验得到不同驱动强度下的耦合强度,如图3(b)所示,可以看到模式耦合强度与驱动强度之间成线性关系。
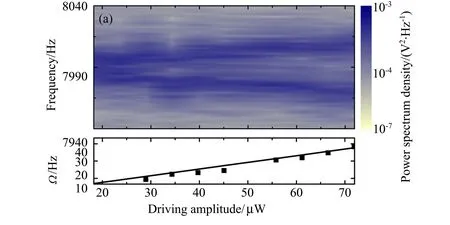
图3 (a)驱动频率ωd/2π=δω/2π=381 Hz时,不同驱动强度下振子的热振动功率谱;(b)不同驱动强度下两模式的耦合强度及其线性拟合结果Fig.3 (a)Thermal oscillation power spectral density of the in-phase mode for different drive amplitude with ωd/2π = δω/2π =381 Hz;(b)Coupling strength of two modes for different drive amplitude with the linear fitting result
为了进一步研究模式频率差对模式间耦合强度的影响,开展了不同模式频率差下模式参量耦合的实验。在免交叉点处,当驱动强度Pd=16 μW时实验测量得到的模式耦合强度达到Ω/2π=30 Hz。随后减小囚禁光功率,使模式间的频率差逐渐增大。当模式间频率差增大至δω/2π=890 Hz时,使模式耦合强度达到Ω/2π=30 Hz所需参量驱动强度Pd=126 μW。在不同模式频率差下,调节驱动强度使模式耦合强度均达到Ω/2π=30 Hz,得到模式频率差与驱动强度的关系,如图4所示。可以看到,随着模式频率差的逐渐增大,达到相同耦合强度时所需要的驱动强度也随之线性增大,表明在相同驱动强度下模式耦合强度与模式频率差成反比,有效耦合强度与驱动强度和模式频率差之间的关系符合Ω=gPdΔ/(4ω2δω)[27]。进一步地,可以利用这一关系在系统远离免交叉点处实现对振子间相互作用强度的测量。作为演示,将对图3(b)线性拟合得到的模式耦合强度与驱动强度之间的系数Ω/2π/Pd=0.55 Hz/μW代入耦合强度的表达式中,得到悬臂梁间相互作用强度为Δ/2π=121 Hz。

图4 不同δω条件下耦合强度Ω/2π=30 Hz时所需驱动强度及其线性拟合结果Fig.4 Drive amplitude for different δω when Ω/2π =30 Hz with the linear fitting result
3 结论
在两模机械系统中,通过对不同模式频率差下模式参量耦合的研究,得到了模式耦合强度与模式频率差之间的关系。实验表明:通过周期性调制囚禁光功率施加参量驱动,当驱动频率等于模式间频率差时可以实现模式间的共振耦合,模式耦合强度可以通过调节驱动强度进行线性调节。当模式频率差改变时,达到相同模式耦合强度时所需的驱动强度也会随之线性改变,表明模式耦合强度与模式频率差之间存在反比关系。利用这一关系,可以在系统远离免交叉点处实现振子间相互作用强度的测量。确定模式频率差与模式耦合强度的关系,有助于基于模式参量耦合的相干操控的设计,实现不同模式频率差下模式间耦合强度的精确控制。此外,在多模机械系统的模式参量耦合的操控方案中,也可以利用该关系设计多模耦合时的相干操控方案,实现对各模式间参量耦合强度的调控。

