Volterra积分-微分方程的高精度数值算法研究
陈 炎, 张新东
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
20世纪初,生物学家Ancona和数学家Volterra提出了经典的“地中海-鲨鱼模型”.1931年,Volterra在“地中海-鲨鱼模型”基础上提出了经典的单种群增长积分-微分模型[1]
Volterra在研究种群动力学增长模型时将遗传性影响因素引入, 得到著名的Volterra积分-微分方程[2]
其中,K(x,t)为积分核函数,f(x)为自由项.Volterra型积分-微分方程在工程和应用科学问题的研究中都有广泛的应用,如纳米流体力学、扩散过程、中子扩散化学和电化学过程、热质传递、弹性力学与动态接触、黏弹性和反应器动力学、流行病建模等[3].正是由于Volterra型积分-微分方程在各个领域的广泛应用,所以关于Volterra积分-微分方程的数值研究也数不胜数,比如谱方法[4-5]、有限差分法[6]、隐式Runge-Kutta方法[7-8]、欧拉法[9]、线性多步法[10]、多项式样条配置法[11]和有限元方法[12]等,以上方法具有各自特点的同时也存在一些不足,例如有限元方法要求计算时划分稠密的计算网格,有限差分法要求很小的差分步长,这将极大地降低分析问题的效率,而本文采用的重心插值配点法不用划分计算网格,并且计算程序编写非常简便,是一种高精度、高效率的数值计算方法.
重心插值配点法已经获得了广泛应用,王兆清等[13]运用重心插值配点法分析了圆环变形及屈曲问题; 邓杨芳等[14]运用重心插值配点法对Cahn-Hilliard方程进行了离散求解.过去一段时间,关于Volterra积分-微分方程的重心插值配点法研究层出不穷,但是目前很多数值研究都没有改变积分项中的未知函数的形式,本文将未知函数变为一阶导数、二阶导数和三阶导数,采用重心插值配点法进行数值模拟,并观察其误差变化.本文首先介绍了重心插值配点法,然后构造了n阶Volterra积分-微分方程的离散格式,最后使用Matlab对四个不同阶数的数值算例进行了数值实现,并验证了方法的有效性.
1 重心插值配点法求解Volterra积分-微分方程
1.1 重心Lagrange插值
重心Lagrange插值是Lagrange插值的改进,2004年,Berrut和Trefethen提出了重心Lagrange插值,重心Lagrange 插值在一些特殊节点下具有很好的数值稳定性[15].
设有n+1个不同的插值节点xj(j=0,1,…,n)和相对应的一组实数fj, 则插值多项式就可以写成Lagrange插值公式
(1)
其中,Lj(x)为Lagrange插值基函数,
令l(x)=(x-x0)(x-x1)…(x-xn), 定义重心权
(2)
也就是wj=1/l′(xj), 则
(3)
将式(3)代入(1), 得到另一种Lagrange插值形式
(4)
利用插值常数1,可得下面恒等式
(5)
将式(5)两边分别除去式(4)的两边, 得到重心Lagrange插值公式
1.2 重心有理插值
重心有理插值就是利用有理函数进行插值, 在2007年,Floater和Hormann提出了一种重心有理插值形式, 该形式无论是在等距节点下, 还是在第二类Chebyshev这种特殊分布的节点下都具有很高的计算精度[16].
将(2)重新定义为
(6)
式中的d是选定的一个正整数, 指标集Jk={i∈O:k-d≤i≤k},O={0,1,…,n}, 则重心有理插值公式就可以写为
重心Lagrange插值公式与重心有理插值具有相同的形式,但插值权重的选择不同,重心Lagrange插值和重心有理插值的插值权分别由(2)和(6)确定.
1.3 Volterra积分-微分方程离散格式构造
针对如下形式的α阶Volterra积分-微分方程, 我们用重心插值配点法对其进行离散

(7)
其中,y(α)和y(β)分别为y的α阶导数和β阶导数,α和β均为自然数.将区间[a,b]离散为n+1个点x0,x1,…,xn,令y0,y1,…,yn为未知函数y(x)在节点x0,x1,…,xn处的函数值. 利用重心插值近似未知函数
(8)
将(8)代入(7), 并将离散节点xi(i=0,1,…,n)代入, 得到
(9)

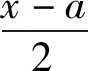
将(9)写成矩阵的形式
(D(α)-Ψ-ΦK)y=f,
(10)

2 数值算例
在数值算例模拟中, 表格中的绝对误差和相对误差与图中的绝对误差分别定义为
err=‖yn-ya‖2,rerr=‖yn-ya‖2/‖ya‖2,err′=yn-ya,
其中, ‖·‖为向量的欧式范数;yn和ya分别为未知函数的数值解和解析解. 为了方便比较, 以下四个算例的解析解和核函数K(x,t)均保持不变, 改变积分项中的未知函数的形式和方程的阶数. 以下算例中的I为单位矩阵, 实现以下算例所使用的软件是MATLAB R2021a, 电脑型号是联想拯救者R7000P.
例1考虑一般形式的一阶Volterra积分-微分方程
在21个等距节点, 21个Chebyshev节点, 8个高斯积分点, 有理插值参数d=10的条件下, 使用重心插值配点法的误差见表1, 从表中数据我们可以看出,在等距节点下, 重心有理插值配点法的计算精度远高于重心Lagrange 插值配点法,在Chebyshev节点下, 重心有理插值配点法的计算精度略高于重心Lagrange插值配点法; 但总体来说Chebyshev节点的计算精度要高于等距节点. 从图1我们可以看到, 在等距节点下, 重心有理插值的计算误差要比重心Lagrange插值小很多, 从图2我们可以发现, 在第二类Chebyshev节点下, 两种配点法的误差变化趋势有着很大的不同, 重心Lagrange插值配点法的计算误差较为稳定, 而重心有理插值配点法的计算误差波动较大. 本算例使用的8个高斯积分点的节点和权重如表2.

表1 例1的计算误差

表2 8个高斯积分点和高斯积分权重

图1 等距节点下例1的计算误差

图2 Chebyshev节点下例1的计算误差
例2考虑如下形式的二阶Volterra积分-微分方程
在21个等距节点,21个Chebyshev节点,8个高斯积分点,有理插值参数d=10的条件下,使用重心插值配点法的误差见表3,从表中数据我们可以看出,在等距节点下, 重心有理插值配点法的计算精度远高于重心Lagrange插值配点法,在Chebyshev节点下,重心有理插值配点法的计算精度略高于重心Lagrange插值配点法; 但总体来说Chebyshev节点的计算精度要高于等距节点.从图3我们可以看到,重心有理插值的计算误差要比重心Lagrange插值小很多;从图4我们可以发现,在第二类Chebyshev节点下,重心有理插值配点法的计算误差较为稳定,而重心Lagrange插值配点法的计算误差变化趋势较大.本算例使用的8个高斯积分点的节点和权重同表2.

表3 例2的计算误差

图3 等距节点下例2的计算误差
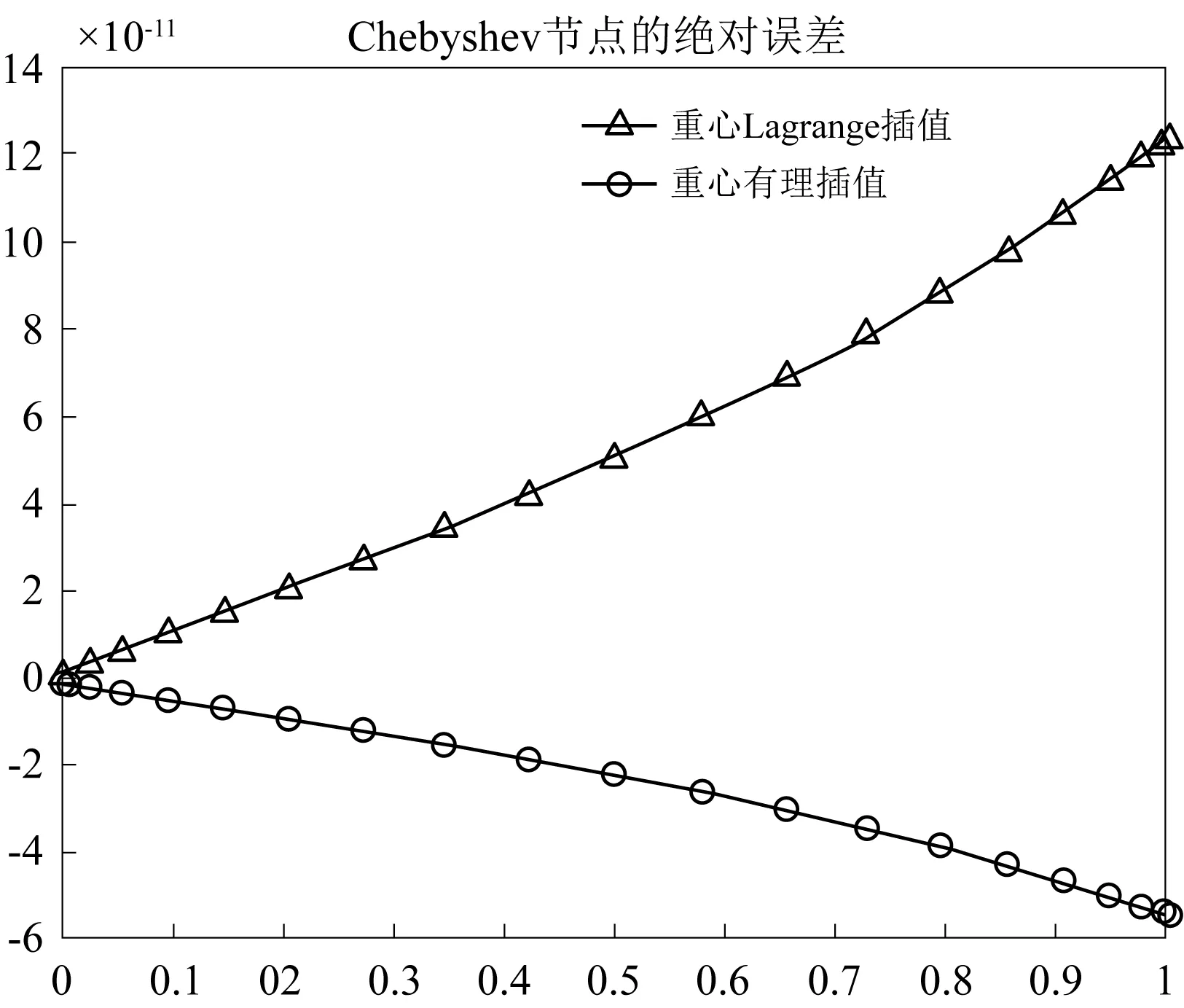
图4 Chebyshev节点下例2的计算误差
例3考虑如下形式的三阶Volterra积分-微分方程
在21个等距节点,21个Chebyshev节点,8个高斯积分点,有理插值参数d=10的条件下,使用重心插值配点法的误差见表4,从表中数据我们可以看出,在等距节点下,重心有理插值配点法的计算精度远高于重心Lagrange插值配点法,在Chebyshev节点下,重心有理插值配点法的计算精度略高于重心Lagrange插值配点法; 但总体来说Chebyshev节点的计算精度要高于等距节点.从图5我们可以看到,在等距节点下,重心有理插值的计算误差要比重心Lagrange插值小很多,从图6我们可以发现,在第二类Chebyshev节点下,重心有理插值配点法的误差较为稳定.本算例使用的8个高斯积分点的节点和权重同表2.

表4 例3的计算误差

图5 等距节点下例3的计算误差
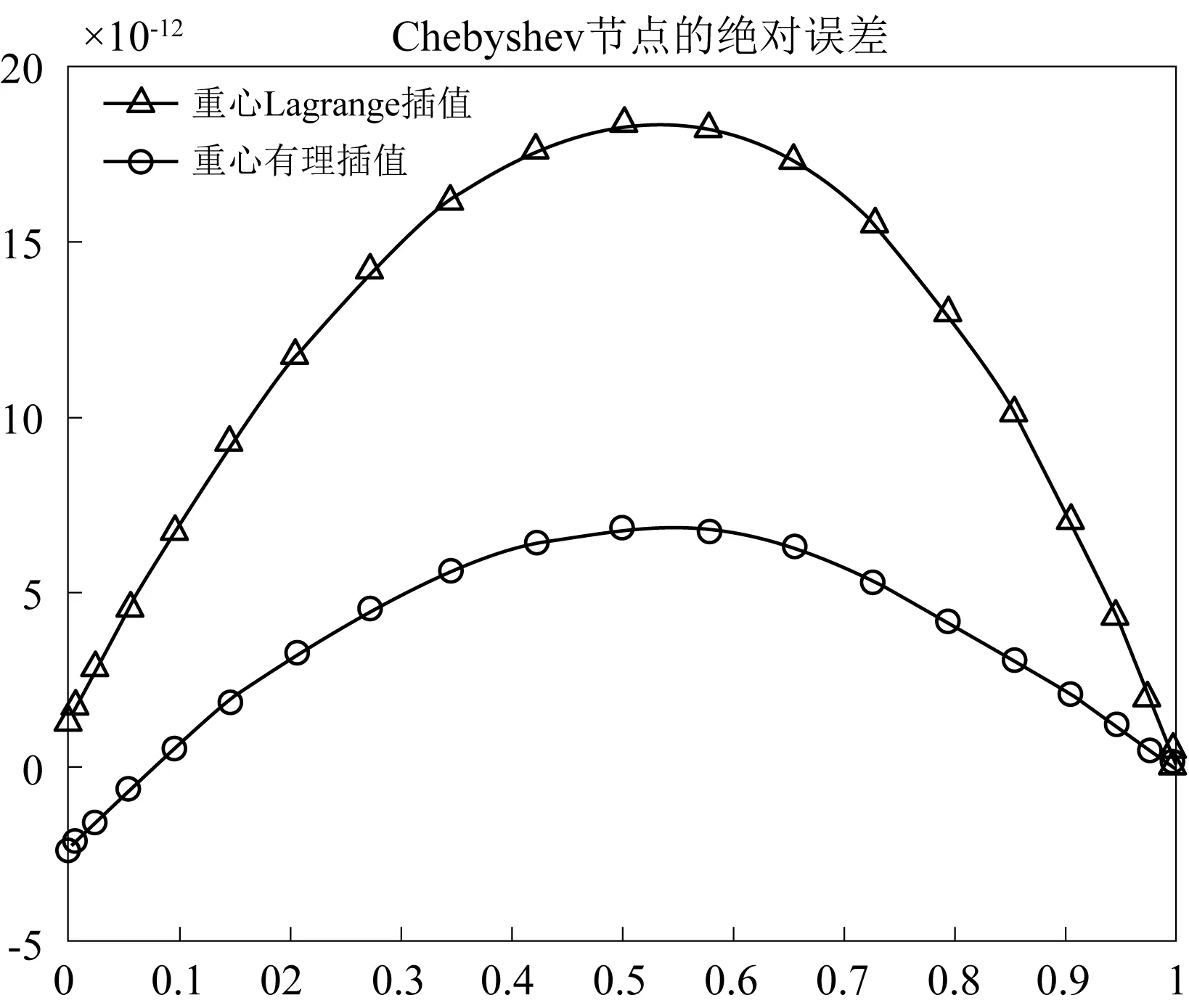
图6 Chebyshev节点下例3的计算误差
例4考虑如下形式的四阶Volterra积分-微分方程
在21个等距节点, 21个Chebyshev节点, 8个高斯积分点, 有理插值参数d=10的条件下, 使用重心插值配点法的误差见表5, 从表中数据我们可以看出, 在等距节点下, 重心有理插值配点法的计算精度远高于重心Lagrange插值配点法, 在Chebyshev节点下, 重心有理插值配点法的计算精度略高于重心Lagrange插值配点法,但总体来说Chebyshev节点的计算精度要高于等距节点. 从图7我们可以看到, 在等距节点下, 重心有理插值的计算误差要比重心Lagrange插值小很多, 从图8我们可以发现, 在第二类Chebyshev节点下, 重心有理插值配点法的计算误差较为稳定, 而重心Lagrange插值配点法的计算误差波动较大. 本算例使用8个高斯积分点的节点和权重同表2.

表5 例4的计算误差
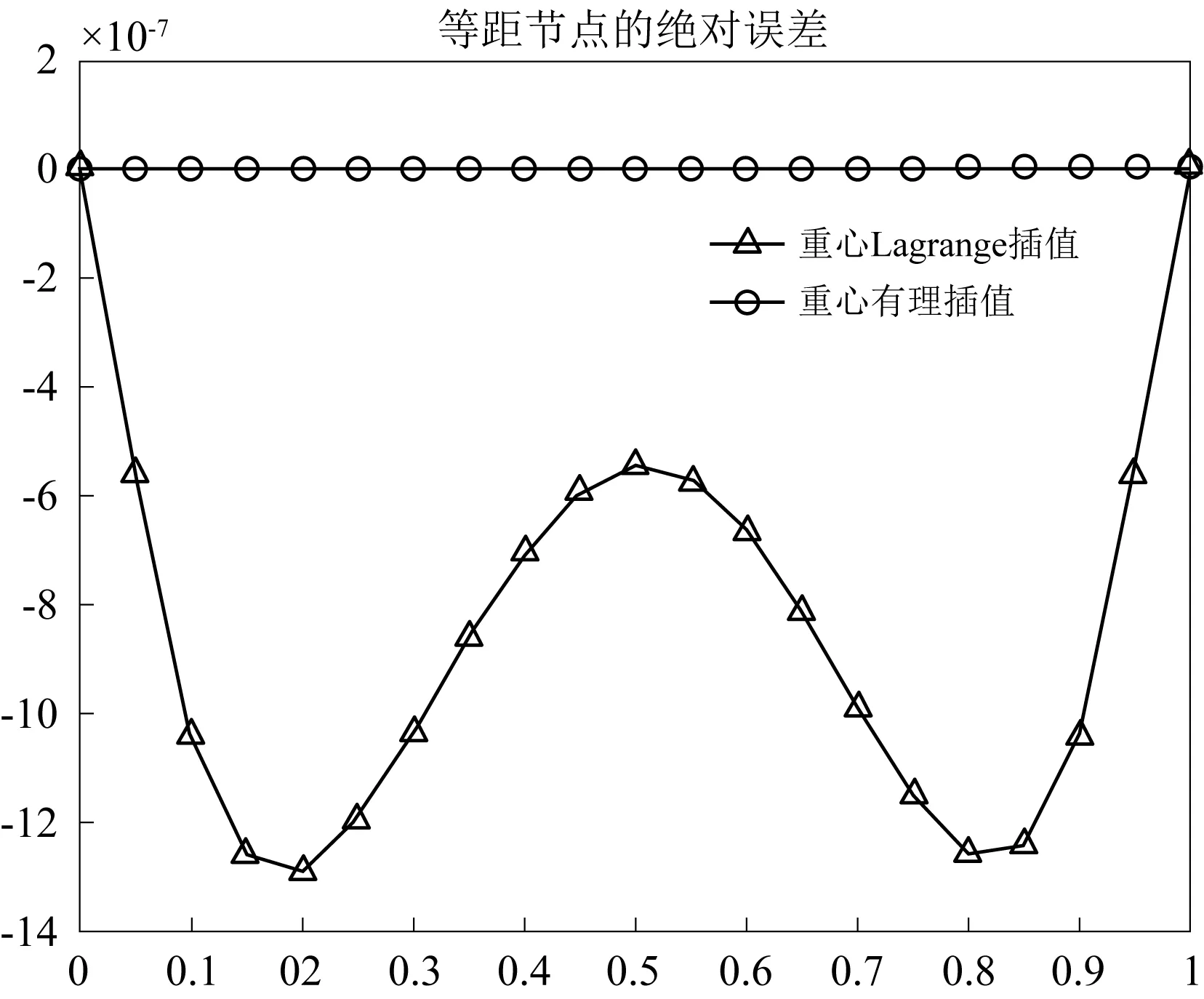
图7 等距节点下例4的计算误差

图8 Chebyshev节点下例4的计算误差
3 结论
本文运用重心插值配点法对Volterra积分-微分方程进行离散求解,并给出四个不同阶数的数值算例的实验结果.通过以上四个算例的误差分析可知,当Volterra积分-微分方程的积分项中含有未知函数的导数时,重心插值配点法依然能保持计算稳定性和较高的计算精度.通过比较以上四个不同阶数算例的误差结果可知,随着方程阶数和积分项中未知函数的导数阶数越来越大,误差也越来越大,其原因是阶数越高,计算程序中的循环次数就越多,计算机完成数值模拟所需要进行的运算就越多,从而导致误差积累变大.

