基于超网络的局部区域新冠肺炎传播仿真研究
刘 泉, 李 贺, 贾媚媚, 于 凯, 张新刚
(1.南阳师范学院 计算机科学与技术学院; 河南省数字图像大数据智能处理工程研究中心,河南 南阳 473061;2.新疆财经大学 公共管理学院,新疆 乌鲁木齐 830012)
0 引言
新型冠状病毒肺炎(COVID-19)的暴发和蔓延给人类社会造成了极大危害,对人民的生命财产和社会经济发展造成了重大损失.世界卫生组织公布,截至2022年11月6日,全球新冠肺炎确诊病例超过6.29亿例[1].对于新冠肺炎的传播和演化机理的研究具有非常重要的意义,引起了学界的极大关注.
目前,针对新冠肺炎的传播不少研究者进行了深入研究.ZHOU等[2]使用SEIR模型对新型冠状病毒肺炎的基本再生数进行了预测研究.YANG等[3]根据优化的SEIR模型,使用深度学习的方法,预测中国新冠肺炎疫情将在二月下旬达到高峰,四月底趋于缓和.SUN等[4]构建了SEIQR模型,用来研究COVID-19在武汉的传播,并考虑了封锁和医疗资源对COVID-19传播的影响.LIN等[5]考虑个人行为反应和政府行为,基于SEIR模型提出了一个新冠肺炎传播的概念模型.GUO等[6]构建了一个具有非局部时滞和逻辑增长的流行病模型,其研究结果表明非局地时滞项在传染病传播过程中起着非常重要的作用.尹楠[7]对有限区域内新型冠状病毒肺炎疫情仿真模拟,并提出了相关建议.汪婧等[8]把感染人群进行细分,通过构建的SEIiRD模型,仿真分析了不同感染人群的传播率对疫情发展的影响.JIA等[9]使用扩展的SIR模型,考虑干预措施的影响,用马尔科夫链蒙特卡罗方法估计意大利的新冠肺炎基本再生数.许小可等[10]根据学生和老师的接触网络数据,模拟了新冠肺炎在校园内的传播.ZHAO等[11]利用MH参数估计方法和优化的SEIR模型,对疫情严重的南非、埃及和阿尔及利亚三种干预情景(抑制、缓解、温和)下的疫情传播进行了模拟和预测.LIU等[12]考虑异质接触网络,模拟了2019冠状病毒病在“钻石公主”游轮上的两阶段爆发.这些研究,大多使用微分方程进行建模,假定个体之间的交互是等概率的,忽略了其所处的接触环境等的差异,而使用元胞自动机和复杂网络等方法可以弥补这些缺陷[13-14].目前,一些研究使用元胞自动机和复杂网络方法对传染病的传播进行了研究,主要集中在网络拓扑结构对传染病传播的影响[15]、接种等免疫措施的影响[16]以及基于信息或行为构建多重网络对传染病传播的研究[17-19].
传统的复杂网络结构中,每条边只能连接两个节点,对多个节点之间的交互作用表达能力较弱.基于此,不少学者使用超网络来描述更为复杂的节点关系.超网络包括基于超图的超网络[20]和基于网络的超网络[21].在本文描述中,超网络主要是指基于超图的超网络.例如,在科研合作网络中,一篇论文对应于网络中的一条超边,论文中的一个作者对应于超边中的一个节点.通常一篇论文中包含多个作者,对应于一条超边包含多个节点.基于超图的超网络目前已经得到不少学者的关注,在信息传播[22-24]、舆论演化[25]、知识传播[26]等多个领域都得到了广泛研究,但是超网络结构下针对密切接触传染病传播的研究还较为少见.
现实世界中人们往往存在于多个密切接触的联系之中,这些密切接触将会导致传染病的传播.例如,工作在同一个办公室、生活在同一套房屋之中、乘坐同一趟航班或参加同一个聚会,这些都会形成密切接触关系.一旦某个个体患上传染病,那这些密切接触的人员都有很大可能被传染.超网络中的一条超边可以包含任意多个节点,一条超边可以对应于一次亲密接触的联系,超边内的节点有更大的概率被相互感染.相较于传统的复杂网络,超网络的这种特性更加适合用来描述密切接触关系,也更适用于密切接触传染病的聚集传播研究之中.
基于上述分析,本文使用超网络来表示社会接触网络.基于SCEIR模型,并考虑潜伏期的持续时间,构建了超网络的新冠肺炎传播模型.使用超网络中的超边来表示有一次密切接触的人群,使模型能够较好地模拟密切接触的范围,由此来研究新冠肺炎的演化过程和传播规律,以期为传染病的防控提供可行性建议.
1 局部区域传染病聚集传播特征分析
在本文中,局部区域是指某一特定的封闭区域,如一个城市、乡镇、社区或校园.在传染病暴发的特定时间段,为阻止传染病的跨区域传播,政府部门采取远距离交通出行限制,实行封城措施.例如中国武汉和意大利米兰为应对新冠疫情采取的封城措施、某些高校在开学之后采取的封闭式管理措施,这些措施将使城市和校园成为一个相对封闭的区域.
新冠肺炎具有典型的聚集传播特征.新冠肺炎感染者以家庭、同事或朋友关系圈集聚的现象被多次报道,这些都说明新冠肺炎传播有很强的聚集特点.2020年2月2日,山东省报告发生多起典型家庭聚集性疫情,截至当日,全省已发现聚集性疫情60起,其中49起为家庭聚集性、6起同事间聚集性、5起集体暴露[27].天津动车客车段聚集性发病是一起非常典型的同事、亲属和密切接触者之间聚集传播的案例.天津动车客车段首位确诊病例杨某某(该市第2例患者),出现在1月21日.该市确诊的第5例患者、6例患者与第2例患者系同事;第8例病例,系天津动车客车段职工;第11例患者为第6例病例家属;第12例和13例患者为第5例病例家属;第16例病例为第5例病例亲属;第17例病例为第5例病例同事;第20例病例为天津动车客车段职工,曾与第6例病例有密切接触史[28].
根据上述传播过程,可以抽象出传播超网络如图1所示.为方便理解,图1中节点编号采用天津市卫健委公布的患者病例编号.e1、e2、e3、e4、e5、e6、e7为超边编号.超边e1包含节点2、5、6、22、28、47,即e1={2、5、6、22、28、47}.
通过对上述的案例传播过程的归纳,可以发现密切接触传染病传播过程具有如下特征:(1)患病个体能够同时将疾病传播给某次密切接触的整个人群;(2)个体存在多个密切联系的关系中,有可能进行多次的密切接触.
传统复杂网络中的边仅可以联系两个节点,只能描述节点之间的二维关系,因而很难将传染病传播中的群体接触描述清楚.然而,超网络中的一条超边可以包含任意一个节点,适合描述多个节点之间的关系,可以更直接地反映密切接触所导致的传染病在人群中的传播过程.超边还可以用于判断节点的密切接触范围,适宜进行传播追踪溯源工作.因此,本文选择超网络来描述个体之间复杂的接触关系,进而构建模型来描述传染病在超网络中的传播过程.

图1 超网络结构下的天津动车客车段职工新冠肺炎传播过程示意图
2 超网络中的新冠肺炎传播模型构建
2.1 超网络的构造
现实中每条超边包含的节点数量(超边基数)往往不是一个固定值[20],如一个家庭关系超网络中,每个家庭的成员数量可能是不相同的.因此,超边基数服从某一分布,更具有现实意义[20].故本文构建的超网络模型为随机超网络,而非均匀超网络.一条超边可以对应于现实社会中的一户家庭,可能是一次同学聚会,也可能是乘坐同一趟航班或同一趟拼车,那么,这趟同乘中的所有乘客就构成了一条超边.
借鉴文献[29]中的构建方法,本文的超网络构造步骤如下:
(1) 初始时,网络中有m0个节点和包含这些节点的一条超边.

2.2 传播模型描述
根据新冠肺炎传播和防治过程,可以将人群分为五种:易感者、密切接触者、潜伏者、感染者、免疫者.易感者为可以被感染的健康人群;密切接触者为同染病者(包含潜伏者和感染者)有过密切接触的人群;潜伏者为已经染病但是尚未表现出症状的人群;感染者为已经染病并且表现出症状的人群;免疫者为表示已经因为治愈并获得免疫、被有效隔离、因病死亡等原因已经不对流行病传播产生影响的人群.将人群抽取为网络中的节点,根据上述五类人群,节点具有对应的五种状态:易感态(S态)、密切接触态(C态)、潜伏态(E态)、感染态(I态)、免疫态(R态).人们之间的关系就构成了节点的连边,网络结构采用2.1小节方法生成.
节点状态的演化过程具体如下:
(1) 初始时,存在N0个处于I态的节点,N1个处于E态的节点,作为初始传播节点,其余节点处于S态.
(2) 在每一个时间步t,对于所有E态节点,当Ti≥1时,选择g条包含该节点的超边,所选择超边包含的所有S态节点将转变为C态,其中有α的概率转变为E态.E态节点随着染病时间Ti的增加,有μ的概率发病,转化为I态;否则,继续处在E态.其中,Ti表示节点i在E态的持续时间,即当节点i从S态转变为E态时,设置Ti=1;在下一个时间步,设置Ti=2,以此类推;当节点从E态变为I态时,将置Ti=0.
(3)I态节点有β的概率被隔离或治疗,转化为R态;否则继续处于I态,随机选择一条包含该节点的超边,所选择超边包含的所有S态节点将转变为C态,其中有α的概率转变为E态.当I态节点被隔离或治疗时,其之前的密切接触者有γ的概率将被隔离,进入R态.
(4)R态节点在以后的时间步中一直处于免疫态,不再对其余节点有影响,退出演化过程.
(5) 当系统中不再存在E态和I态节点时,整个传播过程结束.
由此,可以得到动力学模型如下:
(1)
Sk(t),Ck(t),Ek(t),Ik(t),Rk(t)分别表示t时步超度为k的易感态节点、密切接触态节点、潜伏态节点、感染态节点、免疫态节点的相对密度,满足归一化条件Sk(t)+Ck(t)+Ek(t)+Ik(t)+Rk(t) = 1;ΘI(t)表示一个超度为k的易感节点通过一条超边与一个感染态节点相连的概率;ΘE(t)表示一个超度为k的易感节点通过一条超边与一个潜伏态节点相连的概率.对于度不相关网络,ΘI(t)的表达式[24]为
(2)
通过类似的计算方法,可得ΘE(t)的表达式为
(3)

图2 SCEIR模型传播机理图
3 仿真分析
使用2.1小节中的构造方法生成超网络进行仿真实验.为了去除仿真过程中的随机性影响各参数下的仿真实验均独立重复运行500次.在某地区新冠肺炎暴发的初始时刻,假设网络中有1个I态节点和4个E态节点,其余为S态节点.参数μ取值参照文献[30]中潜伏期分布数据.
3.1 网络结构分析
根据《中国家庭发展报告》,2012年居民家庭户的平均规模为3.02人,1人户数量和2人户数量占全部家庭户的40%[31].借鉴上述的统计信息,本文设置q1=0.34,q2=0.25,q3=0.15,q4=0.1,q5=0.08,q6=0.05,q7=0.02,q8=0.01.构建超网络的初始节点为8,包含在一条超边中.生成网络的节点规模为N= 10000,参数设置为h=2,m=1,计算得到节点超度的均值为7.34.所构建的网络双对数坐标下的节点超度分布如图3所示.所生成的网络中,大部分节点的接触次数较少,仅仅少部分的节点具有较多的接触次数.真实世界中人类接触网络具有小世界和无标度特性[32],从图3中可以看出本文构建超网络的节点超度符合幂律分布,本文构建的超网络可以较好地描述人类的接触模式.
3.2 传染率α对传播范围的影响
传染率α对终态时累计感染人数的影响作用,如图4所示.从图4中可以发现,随着传染率的增大,最终感染的总人数也逐渐增大.网络中节点超度的均值为7.34,代表着每个节点平均可能有7.34次的接触次数.参数d对应含义为实际产生的密切接触次数,当d的取值越大时,说明出行管控越松散,反之则出行管控越严格.从图4中可以发现,终态感染总人数随着d值的增大而增多,说明出行管控力度对最终的感染人数具有重要的影响作用,出行管控越严格,最终的感染人数越少.这与文献[33]的结果相吻合,文献[33]的研究表明暂停城市内公共交通,关闭娱乐场所和禁止公共聚会与总体控制该流行病有关.在其他参数相同的情况下,对比γ= 0.5和0.8,随着γ的增加,终态感染总人数逐渐减少,即加大密切接触者的隔离力度时,累计感染总人数逐渐减少.

图3 节点超度分布图
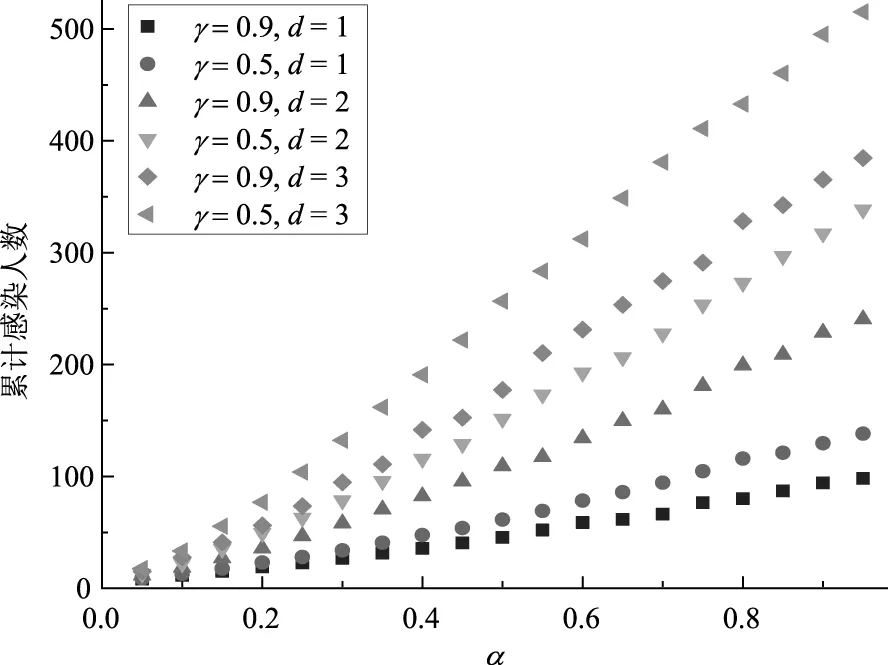
图4 传播率α对累计感染人数的影响(β=0.5)
3.3 参数β对传播范围的影响
参数β表示传染态节点被治疗或隔离的概率,其对累计感染人数的影响作用,如图5所示.为简化起见,在本文中传染态节点一旦被治疗或隔离,将其设置为免疫态,其将不能再传染其他人.从图5可以发现,随着参数β的增大,累计感染人数逐渐减少.当β值较小时,累计感染人数下降幅度较大.特别值得注意的是,随着β值增大到一定程度,即当β> 0.7时,终态的累计感染人数下降幅度不再显著.这说明在医疗资源有限的情况下,可以选择将部分轻症患者居家隔离.当参数取值β= 0.95,α= 0.8,γ= 0.9时,最终累计感染人数值为57,占总人数的比例为5.7‰,说明即使病毒有很强的传染能力,对感染病人和其密切接触者的隔离控制力度较强时,最终的传播范围也是较小的.
3.4 密切接触者被隔离概率γ对传播范围的影响
密切接触者被隔离概率γ表示密切接触者被隔离力度,其值越大,表示隔离力度越强.密切接触者被隔离概率γ对累计感染人数的影响曲线,如图6所示.随着密切接触者被隔离概率γ的增大,累计感染人数逐渐减少.当参数α,β有不同的取值时,曲线展现出相同的变化趋势.对比参数α= 0.5,β= 0.2和α= 0.8,β= 0.6取值时的曲线可以发现,两条曲线几乎重合,说明当病毒的传染性较弱时,对密切接触者采取的隔离力度可以相应地降低.图6的结果表明,感染态节点的密切接触者更有可能被感染态节点传染,其进而传染给其他节点,故密切接触者的追溯和隔离对传染病的传播具有重要的影响.

图5 参数β对累计感染人数的影响(d=1)

图6 隔离概率γ对累计感染人数的影响(d=1)
3.5 隔离措施对传播时间的影响

图7 参数传播β和γ对持续时间的影响(α=0.8,d=1)
传染态节点被治疗或隔离的概率β和密切接触者被隔离概率γ对传播持续时间的影响,如图7所示(传播时间的单位为2.2小节模型中的时步).随着β和γ的不断增大,传播持续时间逐渐减小.说明对感染者和其密切接触者的隔离措施,可以减小疾病的最终传播持续时间.当参数取值为α=0.5,β=0.1,γ=0.05时,传播持续时间有最大值,为56个时步.说明对于传播性极强的传染病,如果隔离管控措施极弱时,预计将有两个月的传播期(这里假设每个时步为一天).当参数取值为β=0.9,γ=0.05时,传播持续时间为17.67个时步;当参数取值为β= 0.9,γ= 0.95时,传播持续时间有最小值,为7.43个时步.值得注意的是,传播持续时间最小值取值情况,对应于传染病在某地暴发的初期即采取最高等级的防疫措施,这种情况一般出现在某地尚未暴发,而其他地方已经暴发一段时间,已经得到人们的广泛重视.
4 结论
针对新冠肺炎传播和控制问题,本文使用超网络来构建社会接触网络,采用SCEIR模型并考虑潜伏期的持续时间和密切接触者的隔离,构建了一种基于超网络的新冠肺炎传播模型,研究影响传染病传播的主要因素.仿真结果表明:出行管控措施越严格,最终的感染人数越少;随着传染态节点被治疗或隔离的概率增大,累计感染人数逐渐减少,但当其增大到一定程度时,累计感染人数下降幅度不再显著,说明医疗资源有限的情况下,可以选择将部分轻症患者居家隔离;对感染者和其密切接触者的隔离措施,可以减少疾病的最终传播持续时间.
本文模型可以较好地模拟局部地区的新冠肺炎传播情形.当病毒的传染性较强时,对密切接触者的隔离力度需要较大;当病毒的传染性较弱时,对密切接触者采取的隔离力度可以相应地降低.本文的工作有助于深入理解新冠肺炎的传播规律,构建的超网络结构是静态结构,相对于实际情况还有一定的局限性,在未来的研究中将构建更加符合实际情况的社会接触网络结构来模拟传染病的传播情况.同时,在传染病实际救治过程中,可能会由于病人过多,存在医疗资源严重匮乏等问题,这也需要在未来研究中优化.
说明:本文研究针对2022年11月之前的数据,故在文字描述上仍采用新型冠状病毒肺炎(新冠肺炎),未采用国家卫健委2022年12月26日的更名——新型冠状病毒感染.

