整体性思维下数学单元教学重构的思与行

王平　任建波

摘 要 “解决问题的策略（选择策略）”是小学阶段最后一次策略教学，是综合运用策略，形成问题解决能力的关键。从策略选择需求不足的现实困境出发，立足教材编排体系、前后内容关联和策略选择逻辑三个方面探寻破解路径，并基于整体性教学思维对整个单元的教学目标、内容架构、流程范式和教学过程进行重构，进而激活策略認知体验多样性，激发选择需要聚焦独特性，升华策略领悟理解共通性，优化策略选择提升灵活性。

关  键  词 整体性思维 学习节律 选择逻辑 单元教学重构

引用格式 王平，任建波.整体性思维下数学单元教学重构的思与行[J].教学与管理，2023（05）：47-49.

最近一次教学研讨，听课内容是苏教版《数学》六年级下册第三单元“解决问题的策略”第一课时“选择策略解决实际问题”。整节课中，教师通过例题和变式练习引导学生使用多种策略解决问题，之后呈现一组“快速反应”练习题启发学生灵活地选择策略，教学环节流畅、目标清晰。然而，在“快速反应”环节时，教师核对结果后追问“你运用了什么策略？”一位同学的回答是“我可以不用策略吗？”教师很快以“他还没有想好，坐下来再想想”做了回应。接下来又是两道变式练习，课堂的推进让人感觉非常“顺畅”。

学生疑惑的神情一直印在我的脑海里，他是真的如上课教师所言“没有想好”？还是他已经想好了，给出的就是自己的疑问呢？笔者又回看了教学视频，在上述教学片段中，笔者逐帧进行课堂观察后发现，当教师问出“你运用了什么策略？”这个问题时，全班大多数同学表情严肃、眼神迷茫，进而逃避与教师眼神的相遇。为什么一定要使用策略？很显然，在例题教学中，学生面对已经可以熟练解决的实际问题时，并没有“选择”策略的真实需要。教学研讨中，教师没有进行策略的独特性、多样性和共通性讨论；也没有将策略与实际问题进行契合度分析，似乎哪种策略都行。但是，策略学习的最终目标是在现实生活中面对真实的问题灵活地做出选择并自觉使用，而不仅仅是套用模式。这恰恰是“选择策略解决实际问题”单元教学的困境所在。

一、整体性思维下“策略”的学习节律

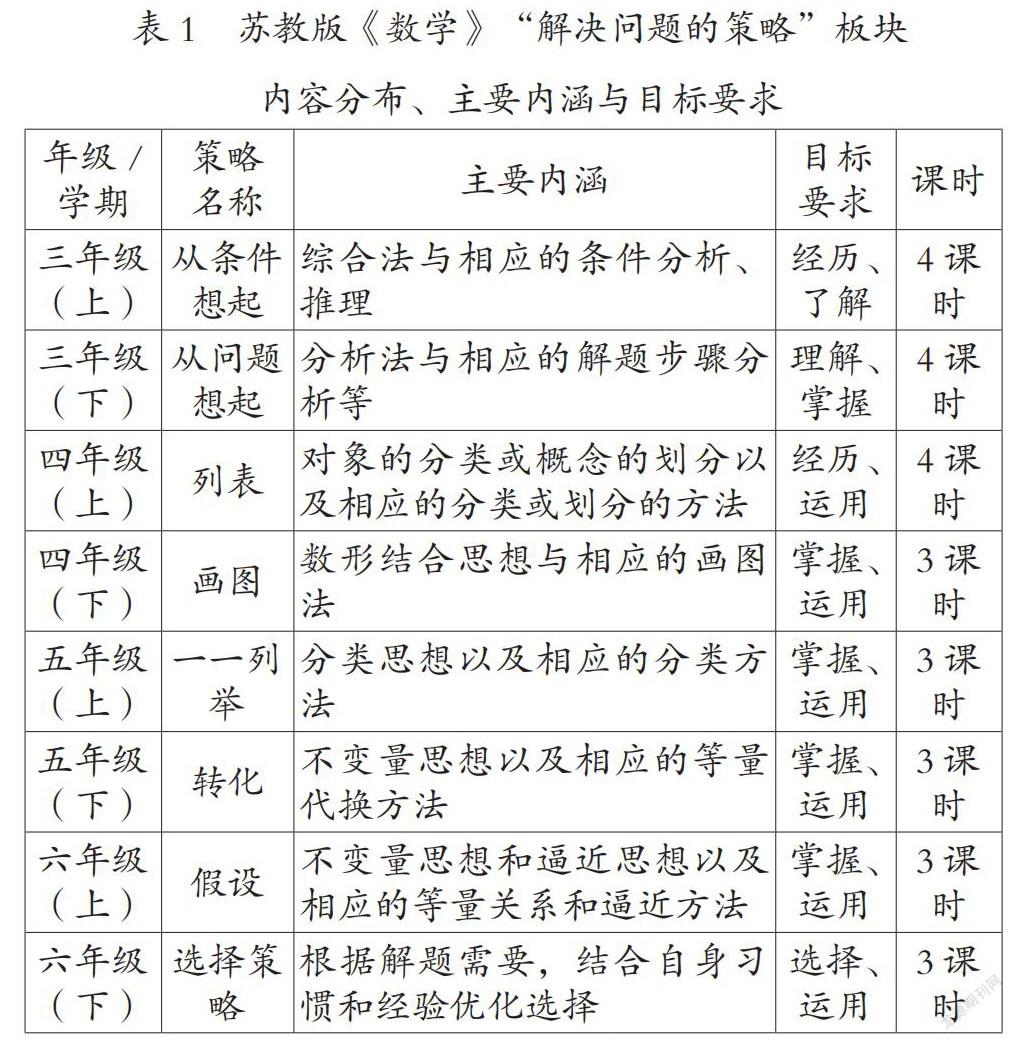
解决问题的策略旨在促进学生“形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力与创新精神”。苏教版《数学》从三年级上学期起，每学期安排了一个专门单元进行教学。具体内容包含：从条件想起、从问题想起、列表、画图、枚举、转化及假设等，此外，六年级下学期最后一次策略教学安排的是“选择策略解决实际问题”。具体编排见表1。

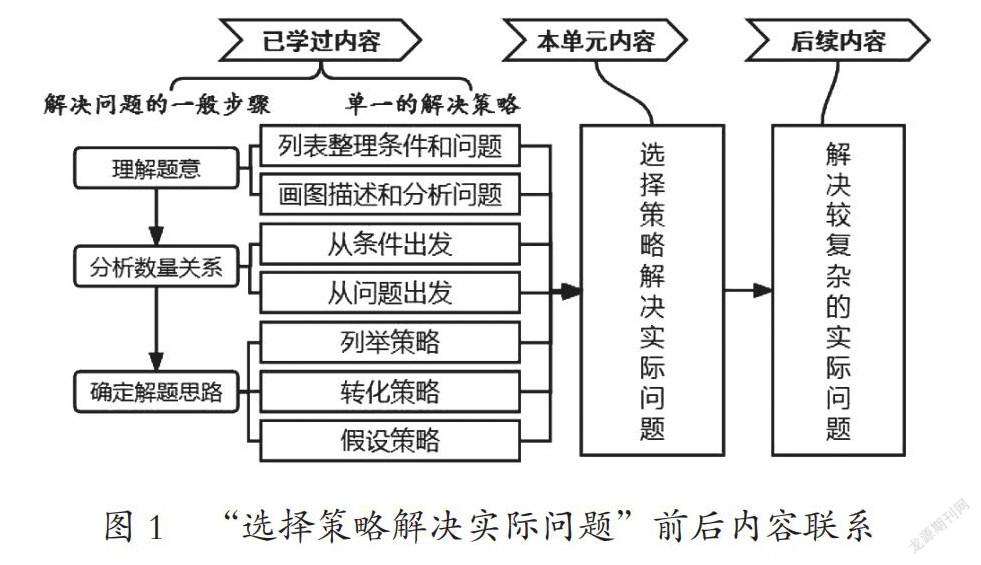
六年级下册“选择策略解决实际问题”这部分内容前后内容的关联如图1。

不难看出，本单元的教学是对前面7次策略教学的横向融通和综合运用，是多种策略配合，形成问题解决能力的关键。目标上呈现出螺旋上升的三个层次：一是能用多种策略分析和解决问题；二是理解不同策略之间的关系，体会其在解决实际问题不同阶段的独特优势；三是能根据实际问题的特点和自身思维习惯等选择适合的策略。

二、整体性思维下“策略”的选择逻辑

1.多样性是策略选择的前提

策略选择是建立在学生具有丰富的解决问题的经验，对常用解题策略有较深的感悟的基础上的。譬如，教学中学生在面对“学校篮球社团男生人数占总人数的。已知女生有21人，男生有多少人？”这样的问题时，能够运用画图策略描述和分析问题，运用从条件或问题出发的策略分析数量关系，运用转化、假设等策略解决问题。

2.独特性是策略选择的依据

策略的独特性体现为策略与实际问题的契合度、对问题解决的贡献度。教学中对学情的分析以及对策略适用情况、优缺点的分析都是策略独特性的必然要求。例如，画图和列表的策略能帮助学生描述条件和问题，便于做出分析，列举、转化、假设，常用于解题思路的确定和解题过程的表述。

3.共通性是策略选择的必然

策略淬炼于具体的解决方法，升华于上位的数学思想，策略的教学最终都是基本思想方法的有意渗透与具体运用。策略在数学思想上具有相通性，如四年级的“列表”和五年级的“一一列举”蕴含的都是分类思想以及相应的分类方法，五年级的“转化”和六年级的“假设”都有不变量思想和相应的等量代换方法。此外，不同的策略在解决问题的过程中也有相通性，如在解决“鸡兔同笼”问题时，学生使用画图的策略和假设的策略，其方法实质是相同的。

4.灵活性是策略选择的追求

策略的选择受到学生自身因素和问题特点的影响。学生已有的解决问题的经验、对策略的认识、自身的思维习惯等都会影响学生对策略的选择，此外实际问题的特点也是重要影响因素。在解决实际问题的过程中学生要根据对问题的表征，判断面临的困难，并从已有的策略中快速做出选择。这种选择有自身的个性特征，也有对策略的深刻理解，是根据不同问题做出的多变选择。

三、以单元教学重构实现“策略”自觉与“策略”灵活

1.单元教学目标的重构是逻辑起点

单元教学目标是在对单元教学内容进行整体分析的基础上制定的，可以避免对教学内容的肢解，避免单课时教学的随意性与盲目性[1]。基于对教材编排意图和策略教学逻辑的认识，为真正激发学生策略选择的需要，促进策略自觉，培养学生的问题解决能力，笔者对苏教版《数学》六年级下册“解决问题的策略”单元教学目标进了整体性重构，确定了单元进阶目标：一是能选择合适的策略分析数量关系，确定解题思路，并能有效地解决实际问题；二是了解策略的多样性、独特性和共通性，理解不同策略在解决实际问题中的作用，能灵活地选择策略，增强策略意识；三是获得分析问题和解决问题的基本方法，体验方法的多样性，培养创新意识；四是进一步感受策略在数学学习和日常生活中的广泛应用，积累策略的运用经验，从中获得成功的体验。

2.单元教学内容的重构是资源再生

学习内容的单元整体分析，主要基于两个方面的考虑：一是这个单元内容所涉及的学科本质；二是分析学生学习这一单元内容的基础条件、主要挑战，以及该内容对学生发展的价值，在此基础上明确单元学习的挑战性主题和指向学生发展的特别是指向核心素养的目标[2]。依循以上教学目标，基于前面7次策略教学的纵向关联，充分尊重学生的选择需要，我们对单元教学内容做了整合重构，框架变化见表2。重构后的单元框架更加突出对多种策略的理解、比较和认识升华，通过纵向提供方法支撑，横向呼应思想方法进而展开教学。

3.单元教学过程的重构是目标达成

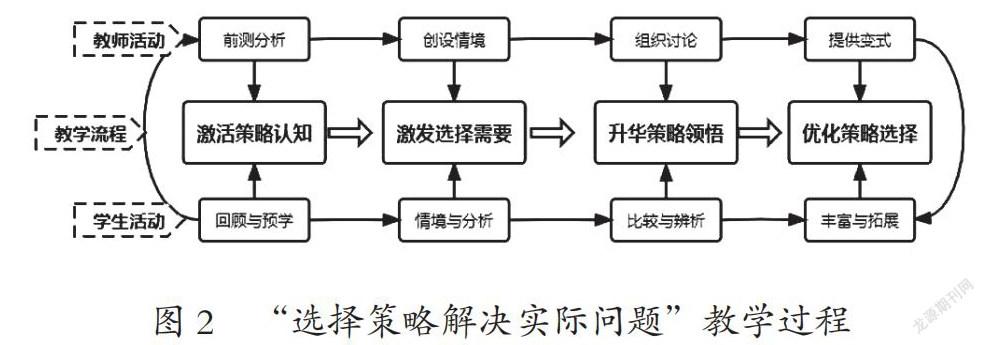
“选择策略解决实际问题”单元的教学，是对单一策略的比较、选择和融通，教学目标和教学内容都与前面的策略教學不同，教学过程也要顺应学生需要，做出调整和建构。单一策略的教学一般注重策略的理解和拓展，教学流程常体现为三个核心环节：激发策略需要—引导策略探索—深化策略运用。活动设计上一般有情境与追问、操作与讨论、变式与拓展等。本单元的教学以丰富的策略知识作为基础，属于已有“前在状态”，可于课前完成，所以环节上增加为四个，活动上也有所不同（如图2）。结合策略选择的逻辑，四个环节分别提升策略的多样性、独特性、共通性和灵活性。

激活策略认知环节先对已有的解决问题的策略进行主动回顾和系统梳理，它是运用多种策略解决问题以及进行比较、选择的基础。为了更好地了解学生已有的学习基础和可能的生长点，使课堂更加聚焦本单元学习的核心任务，可以设置以下三个前置学习任务：任务一，用思维导图整理已经学过的解决问题的策略；任务二，比较这些策略在解决问题中的作用，有什么相同和不同；任务三，根据整理和比较的结果，对这些策略进行分类，并说明理由。在激活已有策略认知后，要通过真实情境下的实际问题激发策略选择的内驱力。教学中，我们将教材例题进行了整合，采取“教师引学例题1→学生自学例题2”的方式推进，围绕核心问题“你为什么采用了这种策略，它有什么作用？”展开讨论交流，促使学生由策略的多样表达快速进入策略独特和问题适切的选择中。在升华策略领悟中先求异，在不同中认识方法的独特性；再求同，在相同中发现策略的共通性。课堂最后呈现一组问题情境，请学生快速地选择策略，深化学生对策略的理解，促进学生将解决问题的策略经验迁移到新的问题中，实现策略选择从“一道题”到“一类题”再到“多类题”的拓展，提升策略选择的灵活性。

最好的学习就是整体学习[3]。除了情感的参与，还需要有整体的知识网络，不能碎片化。单元整体学习的重构，即是从整体性思维出发，立足策略学习的自身节律，遵循策略选择的自在逻辑，激发学生选择的自然需要，促进学生策略选择的自觉性与灵活性。基于此，把单元整体学习的实践落实在单元学习目标的重构、单元学习资源的再生、单元学习过程（评价）的重构三个板块，是“选择策略解决实际问题”教学的一次有益尝试。

参考文献

[1] 胡久华，张银屏.促进学生认识发展的单元整体教学：以化学教学为例[J].教育科学研究，2014（08）：63-68+76.

[2] 马云鹏.“深度学习”视域下的小学“数的运算”教学[J].福建教育，2020（36）：26-31.

[3] 冯嘉慧.深度学习的内涵与策略：访俄亥俄州立大学包雷教授[J].全球教育展望，2017，46（09）：3-12.

［责任编辑：陈国庆］