2022年全国数学高考乙卷理科第21题的解答与思考
郑 良
(合肥市第四中学,安徽 合肥 230000)
2022年全国数学高考乙卷理科(下文简称为全国乙卷)第21题考查函数与导数的综合.第1)小题求具体函数在某点处的切线方程,难度不大.第2)小题难度中等偏上计算量大,相比判断函数零点的个数或已知函数零点个数求参数的取值范围,本题稳中求变、变中有新,创新点为两个零点在给定的区间上,考查了数形结合、分类讨论等思想方法.
1 试题呈现
例1已知函数f(x)=ln(1+x)+axe-x.
1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
(2022年全国数学高考乙卷理科试题第21题)
下面仅对第2)小题进行分析.
2 解法探析
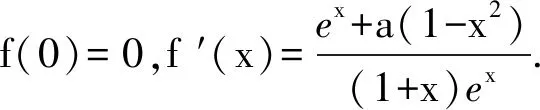
设g(x)=ex+a(1-x2),则g′(x)=ex-2ax.
当a≥0时,若x∈(-1,0),则
g(x)=ex+a(1-x2)>0,
即
f ′(x)>0,
从而f(x)在(-1,0)上单调递增,于是
f(x) 因此f(x)在(-1,0)上没有零点,不合题意. 当-1≤a<0时,若x∈(0,+∞),则 g′(x)=ex-2ax>0, 从而g(x)在(0,+∞)上单调递增,于是 g(x)>g(0)=1+a≥0, 即 f ′(x)>0, 因此f(x)在(0,+∞)上单调递增,即 f(x)>f(0)=0, 故f(x)在(0,+∞)上没有零点,不合题意. 当a<-1时, ①若x∈(0,+∞),则 g′(x)=ex-2ax>0, 从而g(x)在(0,+∞)上单调递增,于是 g(0)=1+a<0, g(1)=e>0, 因此存在x1∈(0,1),使得g(x1)=0,即 f ′(x1)=0. 当x∈(0,x1)时,f ′(x)<0,从而f(x)在(0,x1)上单调递减;当x∈(x1,+∞)时,f ′(x)>0,从而f(x)在(x1,+∞)上单调递增. 根据常用不等式et≥t+1(当且仅当t=0时,等号成立),得 ee-a-e-a>1, 从而 于是f(x)在(x1,+∞)上有唯一零点.又f(x)在(0,x1)上没有零点,即f(x)在(0,+∞)上有唯一零点. ②若x∈(-1,0),设h(x)=g′(x),得 h′(x)=ex-2a>0, 从而g′(x)在(-1,0)上单调递增,又 因此存在x2∈(-1,0),使得 g′(x2)=0. 当x∈(-1,x2)时,g′(x)<0,从而g(x)在(-1,x2)上单调递减;当x∈(x2,0)时,g′(x)>0,从而g(x)在(x2,0)上单调递增,因此 g(x2) g(x3)=0, 即 f ′(x3)=0, 于是f(x)在(-1,x3)上单调递增,在(x3,0)上单调递减. f(-1+e3a)<0, f(0)=0. 因此当x∈(x3,0)时,f(x)>0,即f(x)在(-1,x3)上有唯一零点,在(x3,0)上无零点,亦即f(x)在(-1,0)上有唯一零点.故a<-1,符合题意. 综上所述,所求实数a的取值范围为(-∞,-1). 解法2函数y=f(x)的定义域为(-1,+∞),f(0)=0. 当a≥0时,若x>0,则 从而 f(x)>0, 于是f(x)在(0,+∞)上无零点,不合题意. 当a<0时, 设φ(x)=1+ae-x(1-x2),则 当-1≤a<0时,若x∈[0,1],则φ′(0)>0,φ(x)在[0,1]上单调递增,从而 φ(x)≥φ(0)=1+a≥0. 若x∈(1,+∞),由于e-x>0,a(1-x2)>0,从而 φ(x)=1+ae-x(1-x2)>1. 故当x>0时,都有φ(x)>0,则f ′(x)>0,即f(x)在(0,+∞)上单调递增,因此对任意x>0,f(x)>f(0)=0.故f(x)在(0,+∞)内不存在零点,不合题意. 当a<-1时, ①若x∈(0,+∞),由 φ(0)=1+a<0, φ(1)=1>0, e-x>0, a(1-x2)≥0, 从而 φ(x)=1+ae-x(1-x2)>1, 即 f ′(x)>0, 于是f(x)在(0,x4)上单调递减,在(x4,+∞)上单调递增.由f(0)=0知对任意x∈(0,x4),都有f(x)<0,故f(x4)<0.又因为当x→+∞时, ln(x+1)→+∞, axe-x→0, 所以f(x)→+∞,故f(x)在区间(x4,+∞)上存在零点,有且仅有一个,即函数f(x)在(0,+∞)内恰有一个零点. ②当x∈(-1,0)时, 又φ(-1)=1>0,从而存在x5∈(-1,0)满足φ(x5)=0,且对任意x∈(-1,x5),都有 φ(x)>φ(x5)=0, 即 f ′(x)>0; 对任意x∈(x5,0),都有 φ(x)<0, 即 f ′(x)<0, 因此f(x)在(-1,x5)上单调递增,在(x5,0)上单调递减. 又f(0)=0,则 f(x5)>0, 当x→-1时,f(x)→-∞,因此f(x)在区间(-∞,0)上恰有一个零点. 综上所述,所求实数a的取值范围为(-∞,-1). 解法3f(0)=0,当x≠0时,令f(x)=0,得 故f(x)在区间(-1,0),(0,+∞)内各恰有一个零点,实数a的取值范围是(-∞,-1). 解法4f(x)在(-1,0),(0,+∞)内各恰有一个零点问题等价于直线y=ax与函数m(x)=-exln(x+1)在(-1,0),(0,+∞)内各恰有一个公共点. 从而n(x)在(-1,+∞)上单调递增,又 r(x)≥r(0)=1, 即m′(x)<0.因此,函数m(x)在(-1,+∞)上单调递减.且当x→-1时,m(x)→+∞,m′(0)=-1. 结合图像可知所求实数a的取值范围为(-∞,-1). 评注否定一个命题只需举出一个反例,而肯定一个命题必须要证明.解法1与解法2均为函数最值法,一般是求含参数不等式恒成立、存在性、恰成立中参数取值范围的通性通法,关键是对参数a合理地分类讨论. 由于函数的零点、含参数不等式恒成立等问题是高考的重点与热点内容,因此教师在课堂教学中讲授较多,解法大同小异.限于篇幅,下面仅呈现一个例题. 例2已知函数f(x)=ex+ax2-x. 1)当a=1时,讨论f(x)的单调性; (2020年全国数学高考课标卷Ⅰ理科试题第21题) 下面仅对第2)小题进行分析: 且g(0)=1.下略. 令m(x)=x2+2x+2-2ex(其中x≥0),则 m′(x)=2(x+1-ex), 令n(x)=x+1-ex,则 n′(x)=1-ex, 令n′(x)=0,解得x=0,故函数n(x)在[0,+∞)上单调递减,从而 n(x)≤n(0)=0, 即 m′(x)≤0, 故函数m(x)在[0,+∞)上单调递减,从而 m(x)≤m(0)=0. 令h′(x)>0,得0 分析3由题意,当x≥0时, 当x=0时,a∈R. 当x>0时, 记q(x)=x3-(x2-2x+2)ex+2(其中x≥0),则 q′(x)=x2(3-ex), 从而q(x)在(0,ln 3)上单调递增,在(ln 3,+∞)上单调递减. 记r(x)=ex-x2-x-1(其中x≥0),则 r′(x)=ex-2x-1, r″(x)=ex-2. 令r″(x)=0,得x=ln 2,从而r′(x)在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增,且 r′(0)=0,r′(ln 3)=2(1-ln 3)<0, 代入(0,0),整理得 分析4由题意,当x≥0时, t″(x)=ex-3x+2a. 由t(0)=0,t(x)≥0恒成立,知存在x1>0,使得函数t(x)在x2∈[0,x1]上为不减函数,则t′(x)≥0在[0,x1]上恒成立. 又t′(0)=0,因此存在x2∈[0,x1]使得函数t(x)在[0,x2]上为不减函数,则 t″(0)=1+2a≥0, 评注分析1(命题组提供的参考答案)将原不等式等价变形为g(x)≤1,g′(x)的零点易求.分析2为分离参数法,需要分类讨论,转化为求h(x)在(0,+∞)上的最大值.分析3为图像法,需要分类讨论,转化为y=ax与y=p(x)的图像问题,需要探究p(x)的单调性与凹凸性.分析4为必要性策略,注意到端点值t(0)=0,先探求结论成立的必要条件,然后在必要条件中筛选.若寻找的必要条件与最终的结果相同,直接验证即可. 以含参数不等式恒成立求参数取值范围为例,参数的取值范围是恰成立问题. 1)函数最值法就是判断函数的单调性得到函数的图像.难点在于分类讨论标准的确定,往往因为情况较多甚至出现多级分类而繁杂,体现了“化整为零,各个击破,再聚零为整”.因此,我们要明确目标方向,找准定点、定值,确定合适的分类讨论标准,不宜分类过细. 2)分离参数法的前提是方程或不等式能分离参数,是化归与转化思想的体现.问题转化为研究分离参数后得到的新函数的图像与性质,由于y=a为水平直线,故不涉及函数的凹凸性.难点在于分离参数时可能需要分类讨论,没有体现出分离参数法的优势;还可能已经判断出函数的单调性,但函数在端点处没有意义,需要用到洛比达法则等. (当f(x)=0时,单独讨论),则 显然h′(x)与φ′(x)符号相反,若h′(x)有零点,则φ′(x)与h′(x)的零点相同. 3)图像法是将问题转化为两个函数的大小关系(图像的上下位置关系).若两个函数的凹凸性相反,则它们图像的位置相对精确;若两个函数的凹凸性相同,则它们图像的相对关系不易辨识.一般将问题转化为一次函数与新函数的关系,需要涉及函数的凹凸性. 我们一定要关注解题过程中的逻辑,常见3种求法:①直接求充要条件,如无需讨论的分离参数法;②先利用特殊与一般的关系探寻结论的必要条件,压缩参数的范围,再核验其充分性,如对自变量的区间进行划分,分别求出参数的范围(均为结论的必要条件),(交集)整合后得到结论;③先充分后必要,先发现满足条件的参数的范围,再说明不在此范围内的数不满足条件来验证必要性,如函数最值法先找出满足条件的各个充分条件,(并集)整合后得到结论. 当前教与学中有教师与学生对导数(和解析几何)解答题最后一小题直接放弃的现象.由于最后一小题可能难度不大但过程烦琐,也可能具有深刻而难以挖掘的背景等特点,使得学生即使通过努力也很难得到理想的分数.久而久之,学生遇到该类问题甚至不(认真)审题而选择直接放弃.数学是思维的科学,数学教学是数学思维活动的教学.学习即生活,即如果说生活就是人的茁壮成长和健康发展,那么学习和接受教育的过程其实就是人的生活的重建过程,未战先怯、不战而逃绝不是生活的态度与方式. 无论哪种解法都离不开大量的运算.那么,如何提高学生的运算能力呢?①厚实的积累.一些常见的数据计算、公式的变形等都需要我们平时的理解与识记.②创新之路源自准确的重复.启功先生说过:什么是功夫?功夫就是准确的重复.学生经常运算(不同于单纯地计算)往往能沉下心来,增加耐性,更会减少解题中的卡顿现象,提高变通能力.解法1中确定各零点所在的有穷区间(指区间的端点不含有-∞和+∞的区间)[1],需要学生对零点所在区间端点明方向(比某参照数大还是小,零点用常数还是用参数表示)、定大小(通过函数值的符号确定端点的值).对学生分析问题、解决问题的能力要求更高,突出考查学生的理性思维与综合素养. 很多教师教学内容充斥课堂、讲解照本宣科,多数学生应接不暇、理解浅尝辄止.首先教师要对问题进行深刻的理解,才能够做好必要的铺垫和及时的应对.其次教师还要以合适的方式进行教学.教师理解不代表学生理解;教师讲授不代表学生就能接受;教师不是传话筒,也不是复印机,学生不是知识的容器,更不是一张白纸.因此,教师要设置合适的情境,让学生在情境中感知、感悟、理解,最后师生在持续理解中提升.学习与理解是循序渐进的过程,只有持续地跟进,理解才会逐步得到深化与提升. 那么,如何促进学生领悟、提高学生的思辨能力?首先教师的理解要准确.教师要审慎面对自己的理解,要辨别每个细节.若教师犯(隐藏的)错而不自知,将其传授给学生,则会影响一批学生.其次教师要示范更要注重纠错.解答题主要考查学生思维的严谨性和表达的规范性.当前课堂教学中教师示范居多,夸赞的多;纠错偏少且不够彻底,几乎没有批评.教师不指出学生的错误,学生可能将其逐渐传播.最后教师要让学生及时纠正错误.除了课堂教学,教师发现学生错误最多的是在检测卷中体现.当前阅卷基本上采用踩点给分,其实质是注重结果而忽视过程,导致学生大量的错误未被发现,即使教师发现错误往往也只是象征性的扣分.阅卷应该严格要求,及时记录学生的错误,然后梳理总结,在课堂上及时反馈并查缺补漏,让学生知道每个细节都不能马虎.分数偏高让学生误以为解答正确,错误若没有得到及时反馈则不利于学生改正,力争实现“教、学、评”的一致性.
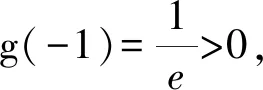
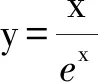
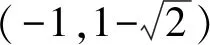
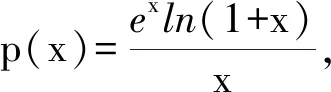
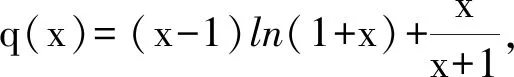
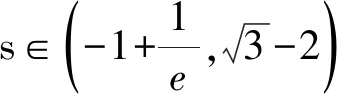
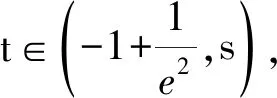
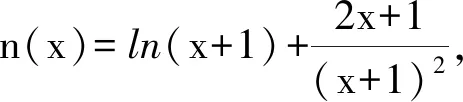

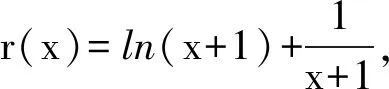
3 试题链接
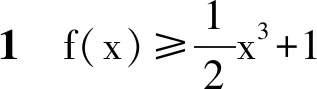
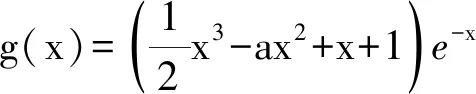
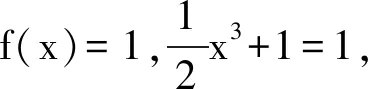
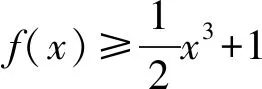
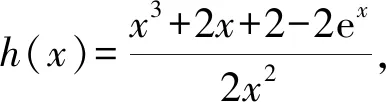
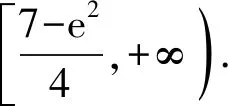
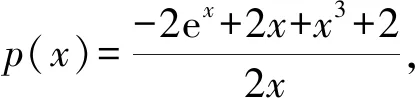
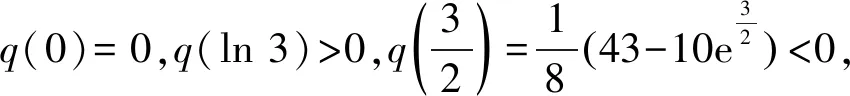
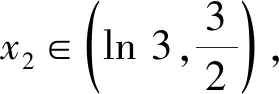
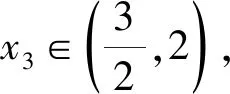
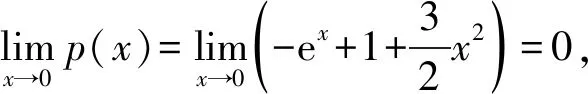
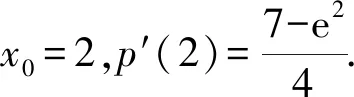
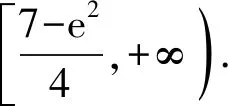
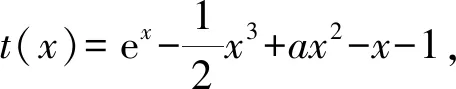
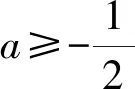
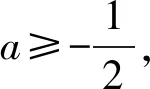
4 几点思考
4.1 理解解法本质,明晰困境突破

4.2 强化理性思维,提高运算能力
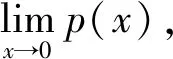
4.3 促进学生领悟,提高思辨能力

