在转化中优化数学运算 在思辨中培育数学素养
——以一道解析几何试题教学为例
肖罗保, 邓 丹
(1.余杭第二高级中学,浙江 杭州 311100;2.临平职业高级中学,浙江 杭州 311100)
高三数学复习时,学生都觉得平面解析几何大题第二问计算烦琐,运算难度大,教师在课堂教学时也深感头痛.然而,平面解析几何又是高中数学教学的重点和难点,在全国各地的高考试题中,通常作为拉开分差的大题出现,在全国卷或新高考卷中分值一般为12分,在浙江卷中占15分,具有较好的区分度.究其原因,平面解析几何难点在于对运算目标对象进行“转化”,难点在于数学运算量大而且烦琐.本文试图通过一道平面解析几何的模拟试题,阐述在解析几何问题的求解中如何进行转化,从而优化数学运算,在思考和辨析中培育学生的数学核心素养.
1 试题呈现

图1
例1如图1,点A为椭圆C1:x2+2y2=1的左顶点,过点A的直线l1交抛物线C2:y2=2px(其中p>0)于点B,C,点C是AB的中点.
1)若点A在抛物线C2的准线上,求抛物线C2的标准方程.
2)若直线l2过点C,且倾斜角和直线l1的倾斜角互补,交椭圆C1于点M,N.
①证明:点C的横坐标是定值,并求出该定值;
②当△BMN的面积最大时,求p的值.
(2020年浙江省周边重点学校数学模拟试题第21题)
2 试题分析
本题考查的知识点是抛物线的标准方程、准线方程、焦点坐标、中点坐标、直线的倾斜角、直线的斜率、直线与抛物线以及直线与椭圆的位置关系问题.在问题的解决过程中,考查学生对基础知识的理解、对基本技能的掌握、对基本思想方法的运用,同时积累基本的解题活动经验.从数学课程的核心素养来看,本题考查逻辑推理、数学运算、直观想象等数学核心素养.
3 教学过程
3.1 第1)小题
3.1.1 问题引导
师:在本题中,点A的坐标是什么?抛物线的准线方程是什么?
设计意图回顾椭圆的顶点坐标、抛物线的标准方程和准线方程等基础知识.
3.1.2 及时追问
师:过点A的直线l1方程该如何假设?
生2:我假设l1的直线方程是y=k(x+1).
生3:我假设l1的直线方程是x=my-1.
3.1.3 比较解法
师:比较这两种直线方程的假设方式,你认为哪种假设更加方便展开计算?为什么?
生4:假设直线l1的方程为x=my-1更加方便,因为直线l1与抛物线C2:y2=2px(其中p>0)联立更简单.
设计意图根据不同的抛物线方程形式,假设相对应的直线方程,联立方程组,减少运算量.
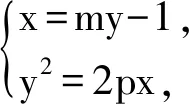
y2-2pmy+2p=0,
从而
在此,如何求点C的横坐标?
3.1.4 耐心启发
生5:我是通过直线方程来求的.因为点C是AB的中点,所以
2yC=yB, yB+yC=3yC=2pm,
但是到这里算不下去了.
师:其他同学能帮助他吗?


于是
师:你是如何想到的?
生6:根据题目需要证明点C的横坐标是定值,我由生5的解法猜想pm2是定值.
师:很好!根据目标,大胆猜想,小心验证结果.还有不同的解法吗?
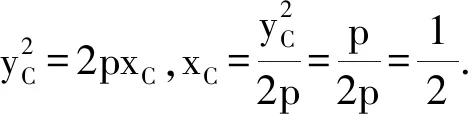

3.2 第2)小题
3.2.1 问题引导
师:接下来,我们看第2)小题.当△BMM的面积最大时,求p的值.请同学们思考:△BMN的面积该如何表达更方便?
生8:计算MN的弦长,再算点B到直线MN的距离h,因此面积公式是
3.2.2 及时追问
师:那弦长MN该如何求呢?点B到直线MN的距离h,该如何求解呢?

整理得
x+my-2=0.
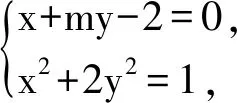
(m2+2)y2-4my+3=0,
从而

师:生9的解题思路非常清晰,也直截了当,需要求什么直接表达出来.可见生9的运算功底很扎实,运算也很仔细.其他同学有没有不同的想法?

图2
生10:我通过生9的解题过程发现直线l2:x+my-2=0过定点(2,0),即直线l2与x轴的交点为定点D(如图2).因此,我再观察发现,由于直线l2的倾斜角和直线l1的倾斜角互补,因此△ACD是等腰三角形,由第1)小题可知
解得xD=2,因此直线MN的方程可设为
x=-my+2,
整理后即为生9所得直线MN的方程.
3.2.3 比较解法
师:生10的解答给我们一个启示,解析几何问题首先是几何问题,应先利用几何图形(△ACD是等腰三角形)建立直观,然后通过转化进而优化代数运算,使得求直线MN的方程更加简洁.还有其他想法吗?
生11:我发现求点B到直线MN的距离可以优化,也就是求△BMN的面积过程可以优化.
师:如何优化求△BMN的面积?
生11:在这个题目中,点B的坐标不用求,因为点C是AB的中点,所以点B到MN的距离可转化为点A到MN的距离.而点A(-1,0)是定点,从而
于是
这样的转化简化了很多运算.
师:同学们很善于动脑筋思考问题,把复杂的问题一步步转化为更加简单的计算问题,在转化中优化了数学运算.接下来我们把结果计算出来.

又
因此

3.2.4 耐心启发
师:通过这道典型的平面解析几何题的解决,给了我们什么解题启示?
生12:解析几何问题,首先是几何问题,应该先利用几何图形建立直观,在转化中优化代数运算,而不是直接去求直线方程,联立求解.应该对图形特点多一些观察,多一些思考.
设计意图让学生总结解题的过程、方法和思考感悟,理解在转化中优化运算过程,在思考辨析中培育数学素养.
4 教学反思
4.1 解析几何问题首先是几何问题,然后才是解析问题
解析几何问题应该先利用几何图形建立直观,然后通过理解运算对象,进而在转化中优化代数运算,使得求解更加简洁.学生的转化能力,不是突发奇想而来的,而是先观察几何图形的特征,然后确定运算的对象、设计运算途径实现的.学生的运算能力的培养不是一朝一夕形成的,也不是一节课几个例题的讲解能够达成的,而是让学生“卷”入课堂教学中来、“卷”入运算对象中来,理解处理问题的思路不同所带来的运算量也不尽相同.
4.2 关注结果,更要关注结果产生背后的思维过程
数学教学活动是数学思维的活动,一堂好课的关键是看学生的“思维参与度”以及有没有高水平的、深层次的思维.教师设置问题,应把学生引入“愤”“悱”的境地,经过思考获得结果.教师不仅要关注获得的结果,更要关注结果获得背后的思维过程,经常问一问“你是怎么想到的?”“你是不是有不同的想法?”“你为什么这样想?”,通过这样一些有效的追问,背后的思维过程就暴露出来了.这样的思考辨析过程有效地提高了知识运用的能力、逻辑思维能力.不知道“为什么”的知识是肤浅的知识,多问“为什么”是从假懂走向真懂的必经之路.
5 结束语
著名数学家波利亚曾说过:“没有任何一个题目是彻底完成了的,总还会有些事情可以做;在经过充分研究和洞察后,我们可以将任何解题方法加以改进;而且无论如何,我们总可以深化对答案的理解.”[1]在处理平面解析几何问题时,教师要不断体会在转化中优化运算、在不断地深入思辨中培育学生的核心数学素养.

