一例多用 创建高效课堂——以古典概型为例

王小芳

(哈尔滨师范大学，黑龙江 哈尔滨 150025)

一例多用源自变式教学，是变式教学一种形式.变式教学基于不同的教学角度，运用多样化的教学方法，向学生展示数学知识与技能的呈现形式和教学内容的变化，并且引导学生在诸多的变化之中探究数学知识与技能“不变”的本质，使学生可以在“变”与“不变”之中从不同的角度和层次对数学现象进行描述性概括，从中归纳数学学习的规律、方法以及事物的一般属性[1].变式教学是我国数学教育的创新，化解了重复操作的弊端，是助推数学教学突破“新高考”改革困境、实现数学“减质增效”、提高数学教学实效性的有效举措之一.一例多用也能从不同角度对同一例子进行思考，从而得出不同的数学知识，如果对例子进行变式——改变题目的某些条件，同样也能得到新知识[2].而这些例子大多是学生在前面的章节中所接触过的例子，很大程度上消除了学生对于新知识的不熟悉感，极大地提高了课堂效率.例如在古典概型章节中，通过投掷骰子、硬币等活动，对活动中随机事件的度量引出概率的定义、对试验共同点的归纳得到古典概型的定义、对试验中某些事件概率的计算过程探究得到古典概型的计算公式.下面以“古典概型”为例进行说明.

1 教学目标

通过设计抛掷硬币的模拟实验，引导学生观察抛掷硬币的实验过程，从中推测硬币哪面朝上和出现点数的可能结果，将问题具体化，自然有序地导入教学.同时，学生从观察抛掷硬币的随机现象之中，通过猜想基本事件的等可能性，归纳概括古典概型的共同特点，培养和发展学生的发散思维和数学抽象思维.此外，学生对基本事件进行猜想的过程，也是判断和识别古典概型的过程，在此过程中学生的逻辑推理能力会得到相应的提升.

通过习题和变式训练，在解决问题的过程中引导学生将实际问题转化为古典概型问题，提高学生问题解决的应变能力以及知识应用的实践能力，提升学生思维的深度，有效提高学生数学思维能力[3].

2 教学过程

2.1 旧例新用，温故知新

师：在以前的学习中，我们讨论过体育彩票摇奖试验、抛硬币试验、掷骰子试验，里面出现过哪些随机现象呢？

预设学生摇出的球为1号、2号……10号；硬币正面朝上、反面朝上；掷出的骰子点数为1，2……6.

师：探索和解释随机事件的关键是其发生的可能性，在数学中通常用“概率”度量随机事件出现的可能性，事件A的概率用P(A)表示.

设计意图通过前面学习过的实例进行引入，旨在一例多用，从不同角度，从已经学习过的实例中体悟新知识[4].从对随机事件可能性度量的角度引出概率的定义，让学生从整体架构上把握新旧知识的联系，为后面探索古典概率的数学模型做准备.

2.2 旧例巧用，建构知识

师：通过对大量随机事件的试验和观察，可以估计某一随机事件发生的可能性，那么是否可以借助数学模型，通过分类讨论、转化与化归的数学思想解决概率问题呢？

问题1观察下面3个试验，它们有什么共同特征？

1)一副扑克牌(除大小王外)共有4种花色，每种花色有13张牌，现选择“方块”花色，将13张方块花色的纸牌随机打乱后，随意抽取出一张纸牌；

2)抛掷一枚质地均匀的硬币；

3)抛掷一枚质地均匀的骰子.

预设学生从质地均匀可知每一个事件发生的可能性是相等的.

追问1分别写出试验的样本空间及样本点.

预设学生试验1)中样本点有13个，可能抽取出的纸牌为方块A、方块2、方块3……方块K，试验1)的样本空间Ω1={A,2,3,4,5,6,7,8,9,10,J,Q,K}；试验2)中样本点有2个，即硬币正面朝上或者反面朝上，“正面朝上”用m表示，“反面朝上”用n表示，则试验2)的样本空间Ω2={m,n}；试验3)中样本点有6个，即掷出的点数可能为1,2,3,4,5,6，因此试验3)的样本空间Ω3={1,2,3,4,5,6}.

追问2观察你的结果，它们有什么共同特征？

预设学生样本空间为有限样本空间.

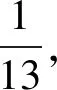
设计意图利用对旧例的共同特征(等可能性和有限性)的观察和发现，提炼出这一类试验所具有的共同特征，培养学生抽象归纳的能力.通过对这3个试验中的样本点和样本空间的书写，培养学生数学“三会”能力.

辨析以下两个试验是否是古典概型：

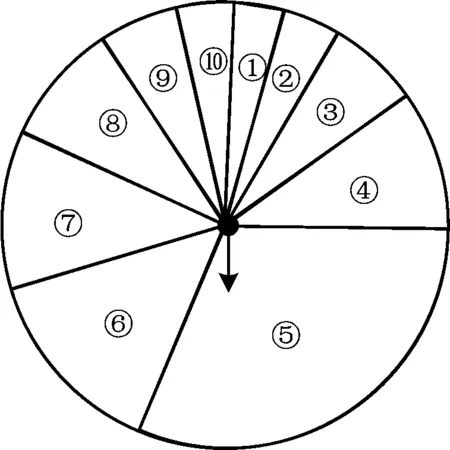
图1

1)改变抽奖游戏规则，如图1所示，转动抽奖转盘，随机抽取一个数字选择对应的奖品.这是古典概型吗？

2)在打靶子游戏中，小明向空白靶内随机抛投带有颜料的纸团，假设纸团落在靶内的任意一处的机会是均等的.这是古典概型吗？

预设学生1)不是，不满足等可能性;2)不是，不满足有限性.

师：你能归纳判断一个试验是否是古典概型的方法吗？

预设学生必须同时满足有限性和等可能性的特征.

设计意图概念辨析，旨在让学生明确概念的本质，在头脑中形成有关古典概型清晰的概念，通过辨析题，学生自己归纳出判断古典概型的方法，发展逻辑推理的数学素养，掌握判断古典概型的方法.

2.3 旧例变式，概念应用

问题2根据以下两个随机事件，思考如何衡量事件1与事件2发生结果的可能性？

1)抛掷一枚质地均匀的骰子1次，事件1=“点数是2的倍数”.

2)抛掷一枚质地均匀的硬币3次，事件2=“恰好一次正面朝上”.

追问1类比问题1，写出这两个试验的样本空间和样本点，以及事件1和事件2所包含的样本点.

预设学生问题1)中样本点为1,2，3,4,5,6，样本空间Ω1={1,2,3,4,5,6}；事件1=“点数是2的倍数”所包含样本点为2,4,6；问题2)中用正表示硬币“正面朝上”，用反表示硬币“反面朝上”，样本点为(正正正)、(正正反)、(正反正)、(正反反)、(反正正)、(反正反)、(反反正)、(反反反)，样本空间Ω2={正正正，正正反，正反正，正反反，反正正，反正反，反反正，反反正}.

追问2计算事件1和事件2发生的可能性.

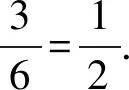
设计意图通过具体的例子，使得学生利用已有的知识经验，初步感知古典概型概率的计算方法，并在此基础上为后面的把特殊问题一般化推导出古典概型概率计算公式打下基础.

2.4 旧例再用，知识巩固

例1抛掷两枚质地均匀的骰子(标记为Ⅰ号和Ⅱ号)，观察两枚骰子可能出现的基本结果.

1)写出此试验的样本空间，并判断其是否为古典概型.

2)求下列事件的概率：A=两个点数之和是5；B=两个点数相等；C=Ⅰ号骰子点数大于Ⅱ号骰子点数.

教师讲解示范：1)可使用表格法(略)或树状图法(如图2)列举样本空间：

图2

因此样本空间Ω={(m,n)|m,n∈{1,2,3,4,5,6}}，其中共有36个样本点.

2)A={(1,4),(2,3),(3,2),(4,1)},有4个样本点,故

B={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}，有6个样本点，故

C={(m,n)|m>n,其中m,n∈{1,2,3,4,5,6}},有15个样本点,故

变式1同样质地均匀的两枚骰子但是不编号，回答下列问题：

1)写出这个试验的样本空间，并判断这个实验是否为古典概型；

2)求事件A的概率，其中A=“两个点数之和是5”.

想一想为什么相同的事件标记号和没有标记号会产生不同的结果？

设计意图让学生应用古典概型公式解决生活中的实际问题，学会计算古典概型的概率；通过变式教学，让学生区分古典概型和其他试验的区别，进一步明确古典概型的特征——等可能性，即若试验结果的可能性不相等，则不是古典概型，进而不能用古典概型的公式求解问题.

例2在数学模拟竞赛中，有8道备选题，其中包括5道甲类题和3道乙类题，小张同学从8道题中任意抽选2道题进行解答.

1)小张同学所抽取的2道题都是甲类题的概率；

2)小张同学所抽取的2道题不是同一类题的概率.

设计意图学生通过猜想小张同学抽取甲、乙两类题的概率，列举试验的样本空间，体会在平时考试中的古典概型，熟悉用数学语言表达解题过程，并且感知概率越小猜对答案越难.

问题3你能通过以上例题归纳概括求解古典概型问题的一般思路吗？

师生活动学生在教师的引导下归纳求解古典概型的思路，如图3所示：

图3

设计意图通过思维导图的形式，帮助学生高效理解求解古典概型概率问题的一般方法.

2.5 课堂小结，凝练升华

1)知识：古典概型及其概率计算公式.

2)研究思路(如图4所示)：

图4

3)方法：列举法、树状图.

3 教学反思

3.1 关注学生，充分考虑已有经验

本节课立足于学生的前理解能力，采用温故知新的教学策略，从旧例出发，不同方向、不同角度进行变式、探索.在温习旧知、探究新知的过程中，促进学生理解和掌握新知，实现新知与旧知的有效衔接.

3.2 深挖教材，充分利用旧例

教材中的每个素材、每道例题都有深刻的含义，本节课就是从教材中的例子出发，从不同角度发散出新知识.从随机事件发生可能性大小的度量得出概率的定义，通过概括随机现象的共同特征，得出古典概型的定义，通过对随机事件可能发生的结果的计算得到古典概型概率的计算公式.

3.3 巧用变式，化繁为简

变式教学有着丰富的内涵，本节课中多次利用同一组例子(抽奖、抛硬币、掷骰子)，避免了重复操作的弊端，提高了课堂效率.