对一道病题的教学与思考

李 昌

(南京师范大学灌云附属中学，江苏 连云港 222200)

1 问题的提出

在学生参加的一次联合考试数学试卷中，有如下试题：

在评讲试卷时，有的教师认为：虽然这是一道病题，但其依然可以解答，且学生普遍得分较高，也达到了考查知识掌握情况和运用水平的目的，因此不需要评讲.但笔者认为：这有掩盖回避之嫌，学生已经接触到了这一病题，若不辨析病因、澄清错误，则很可能会强化学生的片面认知.以下是笔者对此题的教学和思考，期望得到广大读者的批评与指正.

2 发现与辨析

思索片刻后，学生们纷纷举手发言.

师：这种几何关系对△ABC有什么限制？

生(众)：△ABC的边长都不能超过外接圆的直径2.

师：条件“M是边AB上一点，且CM=2”表明了什么？

生2：只有当CB是圆的直径且点M与点B重合时，才能满足CM=2.

生4：当点M与顶点B重合时，第2)小题的∠BMC也就无意义了.

师：由此可见，这是一道病题，题目的一些条件无法自洽，致使要计算面积的三角形不存在.可是，对于一个不存在的三角形，为什么还能求出面积呢？

生5(思索讨论后)：第1)小题明确给出了三角形的3条边长，这些数据满足任意两边之和大于第三边，它们对于计算三角形的面积是充分的.

师：三角形内接于圆，三角形中的线段应受到圆的限制.命题者可能忽视了这一几何背景，割裂了数据之间的逻辑关系，出现了“局部大于整体”的逻辑错误.

3 修正与验证

生6：有些线段太长而外接圆太小，可以扩大外接圆或者缩短线段.

师：即有“扩圆”和“缩线”两种方案.凡事预则立，修正数据时首先要考虑如何减少运算的复杂性.从这个意义上看，大家认为哪种方案容易实施呢？

经过短暂的讨论后，学生们一致选择了“扩圆”的方案.

师：如何扩圆呢？如何修正数据对计算的影响较小？

生9：让AC成倍地增加.

师：用2倍AC、3倍AC一次次地试，直到合适，如何？

生10：没必要，可设AC是原来的k倍.

师：在∠BMC有意义的前提下，求第2)小题中BM的长度，结果用k表示.

生(众)：只需当外接圆直径大于2，即k>2时，∠BMC有意义.对原解答进行适当地修正，其中的主要步骤和数据为：

在△BCM中，由余弦定理得

CM2=BM2+BC2-2BM·BC·cos∠MBC，

代入上述数据，化简得

容易发现:当12时，BM1和BM2都为正数.这是否表明一个圆中有两个不同的内接△ABC，它们的边AB上各有一点满足题意？或者，圆中只有一个内接△ABC，其边AB上有两点M1和M2都满足题意？

先在GeoGebra软件中直观地验证如下两个问题：一是在给定的△ABC中，边AB上满足CM=2且∠BMC+∠BAC=90°的点M的个数；二是在给定的圆中，有多少个内接于圆的△ABC，其边AB上存在点M满足CM=2且∠BMC+∠BAC=90°.

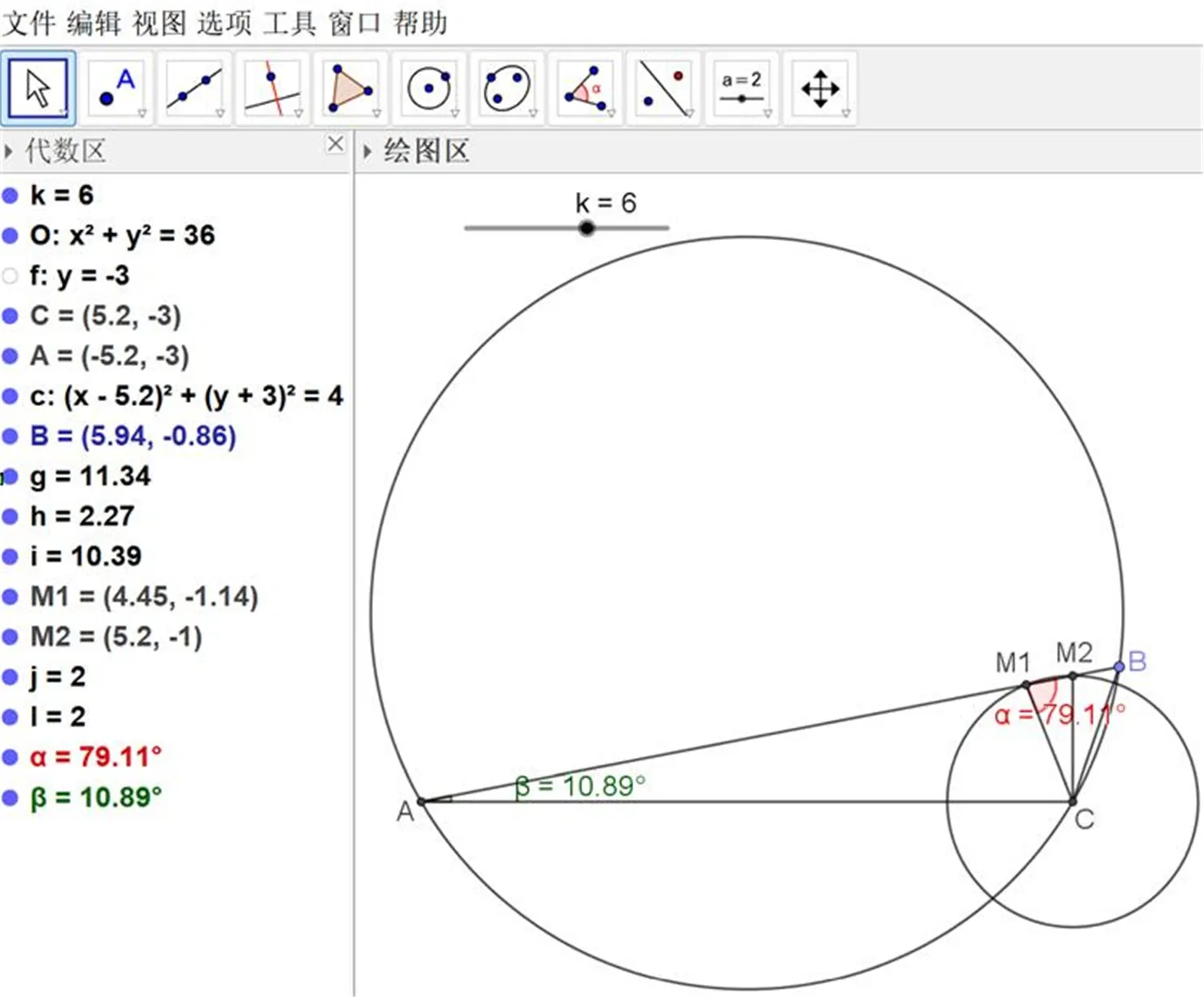
图1

4 分析与改进

sin∠BCM=sin[π-(∠B+∠BMC)]

代入数据,化简即得

5 教学的思考

命制试题具有挑战性和创造性，即便命题者字斟句酌，小心谨慎，但稍有不慎，错题、病题仍会出现.因此，教师在面对病题时，不应刻意回避掩盖也不要大惊小怪，而应该冷静思考，仔细揣摩命题的思路，多方辨析病题的成因，深度探究修正的方案，合理设置教学的路径，努力把病题变成一种生成性的教学资源，发挥其独特的教学价值.在本例中，通过对病因的辨析，学生对正弦定理的认识，从沟通边角关系的工具上升到三角形的几何不变量；通过对数据的修正，学生体验到数学运算的思考性，认识到避免盲目运算的重要性；通过对解法的验证与改进，学生对余弦定理解三角形可能产生增解的原因有清晰而深刻的认识.总之，通过此题的辨析，学生对解三角形的认知从工具性理解上升为关系性理解.

辨析病题的思维遵循从证伪到求是的路径，这与解题教学的思维路径大不相同.解题教学和解题训练呈现给学生的都是正确的数学命题，学生的思维活动几乎被限定在正确的逻辑推理框架之内，因而无法经历题目形成过程中的去错、去伪和去劣的过程；学生思维的路径也几乎被限定在从证实到求是的轨道之上，没有机会进行逆向的和悖向的思维，不利于反思性思维的形成和发展.这种证实求是的训练和教学，容易压缩知识的形成过程，导致学生只知是什么样，而不知为什么是这样，容易造成知识理解的表面化[1].在本例中，学生通过对题目条件的辨析，发现了病因在于条件无法自洽；通过对数据的修正，理清了形成题目的思路和过程；通过对解法的改进，认识到正弦定理和余弦定理在解同一类三角形问题上的差异.在这个过程中，学生有证伪求否的悖向思维活动，也有证实求是的正向思维活动；学生执行了从条件到结论的正向推演，也进行了从结论到条件的逆向推理.由此可见，病题辨析可以实现求是与去伪的融合[2]，能够改变学生的思维惯性，培养和发展反思性思维.

病题教学的实施，需要学生的思维全程深度参与，体现为数学知识和思想方法的主动运用.在本例中，学生若仅靠记忆正弦定理的符号意义，对三角形与其外接圆之间的联系无深刻的整体理解，则学生很难发现条件之间的容斥关系；若仅会按部就班地执行正弦定理、余弦定理的运算，而对正弦定理中因改变三角形的内角B带来的复杂运算缺少预判，则无法理解更不能想到把边AC成倍增加的方案.由此可见，病题辨析与修正的过程不是传递知识的过程而是主动运用知识的过程.学生在知识的运用中，自然触及知识的逻辑联系、知识背后的价值方法，对知识的认识和理解将更加深刻.从这个意义上看，病题辨析的透彻程度决定了学生的理解深度.