柔性基础下等芯型水泥土复合桩荷载传递特性分析
陈昌富 ,陈苏淑 ,朱世民 ,蔡焕
(1.建筑安全与节能教育部重点实验室(湖南大学),湖南 长沙 410082;2.湖南大学 土木工程学院,湖南 长沙 410082)
劲芯水泥土复合桩是在尚未凝结的水泥土桩内插入高强度预制混凝土芯桩(大多数为等截面芯桩)而形成的复合桩.它充分发挥了芯桩强度高和水泥土桩表面积大的优点[1-4],具有较高的承载力和良好的经济效益,被广泛用于地基加固和基础工程中.
对于刚性基础下等截面劲芯水泥土复合桩的荷载传递特性,已有学者展开了研究.俞建霖等[5]假定芯桩-水泥土界面和水泥土-土体界面符合理想弹塑性荷载传递模型,分析得到了刚性基础下等芯型水泥土复合桩砼芯、水泥土桩和桩周土三者相应的应力位移表达式.刘汉龙等[6]基于大尺寸模型试验,对带承台的高喷插芯组合单桩的荷载传递规律进行了研究分析.
对于柔性基础下等截面劲芯水泥土复合桩的承载特性研究,张振等[7-8]基于室内试验结果分析了短芯型水泥土复合桩承载路堤失稳破坏模式;Voottipruex等[9]通过现场变形监测与静载荷试验,证实了路堤荷载下劲芯水泥土复合桩相比水泥土搅拌桩在沉降与变形控制上具有优越性;叶观宝等[10]假定界面剪应力与深度或相对位移呈线性关系,导出了桩顶设置垫层的劲芯水泥土复合地基芯桩、水泥土桩、桩周土三者之间应力比的计算公式.但目前鲜有考虑界面剪应力非线性特性的柔性基础下劲芯水泥土复合桩荷载传递规律的研究成果.
当劲芯水泥土复合桩位于刚性基础下,其中芯桩、水泥土桩、土体在桩顶处是处于位移协调的变形模式.但是,在柔性基础下,芯桩、水泥土桩、土体在桩顶处就会产生差异沉降,并引起各界面间的相对位移,从而使桩的荷载传递规律、摩阻力分布、沉降特性呈现截然不同的状态.因此,有必要对柔性基础下劲芯水泥土复合桩的荷载传递特性进行研究,以便深入系统地了解柔性基础下劲芯水泥土复合桩的工作性状,为工程实践提供设计依据.
相较于单一材料桩,劲芯水泥土复合桩的内外芯结构使得荷载传递机理更为复杂,内外芯在荷载作用下势必产生相对位移与剪切,芯桩-水泥土桩-桩周土之间的相互作用是研究劲芯水泥土复合桩荷载传递规律的重要研究对象.分析劲芯水泥土复合桩的荷载传递特性,常采用荷载传递法[11-12].荷载传递法的关键是选取能够较真实地表征桩-土界面特性的荷载传递模型.为简化计算,任连伟等[13]、徐礼阁等[14]与蒋德松等[15]采用理想弹塑性模型来表征芯桩-水泥土桩界面的荷载传递特性,Zhou 等[16]则采用两折线模型表征芯桩-水泥土桩界面的荷载传递特性.但是,这些荷载传递模型由于形式过于简单,难以较贴切地表征芯桩-水泥土界面的剪切软化过程[17-18].
鉴于此,本文在已有研究成果的基础上,首先对柔性基础下等芯型水泥土复合桩的受力与变形模式进行分析;然后,引入双指数函数型荷载传递模型表征芯桩-水泥土界面的剪切软化特性,采用理想弹塑性模型刻画水泥土-土体界面的荷载传递特性,基于荷载传递法建立芯桩、水泥土桩、土体三者之间的递推关系式,并结合迭代计算方法,提出一种柔性基础下等芯型水泥土复合桩荷载传递规律分析计算方法;最后,采用现场试验结果和工程案例来验证本文提出方法的可靠性.
1 等芯型水泥土复合桩荷载传递分析方法
1.1 受力变形模式分析
对于工程中常见的等芯型水泥土复合桩,它在柔性基础下的受力变形模式如图1所示.
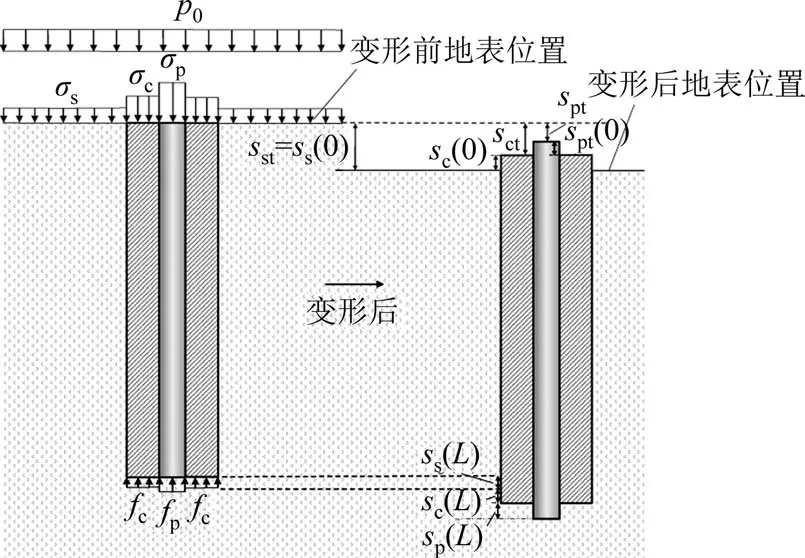
图1 等芯型水泥土复合桩受力变形示意图Fig.1 Schematic for the stress and deformation mode of equal-core stiffened deep mixed pile
等芯型水泥土复合桩在柔性和刚性基础下的变形模式存在显著差异.柔性基础下等芯型水泥土复合桩的桩顶处不再符合桩土等应变假设,即芯桩、水泥土桩和桩间土的位移不协调.现以桩顶中心为坐标原点建立坐标轴,取正方向向下.将上部基础对芯桩、水泥土和桩间土的作用视为不同刚度的弹簧体系,在上部荷载p0作用下,假设桩顶处芯桩、水泥土桩和桩周土所受压力为Pp、Pc、Ps,则相应的应力分别为σp、σc和σs,并令

式中:npc、ncs分别为芯桩与水泥土桩、水泥土桩与土在土桩顶处的应力比.npc和ncs可根据经验数据综合确定,也可通过计算得到,即:将上部基础当成弹性地基板(梁),芯桩、水泥土和桩间土当成不同刚度的弹簧的模型,将基础分段后,建立挠度的差分方程组,再将地基沉降与基础挠度耦合并迭代计算,进而获得npc、ncs的值.
桩顶处,芯桩、水泥土桩与桩周土在σp、σc和σs作用下产生的沉降分别表示为spt、sct、sst.桩体在桩顶处的位移模式与应力比npc、ncs有关.若应力比较大,芯桩相对于水泥土桩、水泥土桩相对于土产生向下的位移.反之,则会产生向上的相对位移,桩体刺入垫层.图1所示为桩体刺入垫层时的情况.
根据变形关系,等芯型水泥土复合桩芯桩桩顶的沉降spt可表示为:

水泥土桩桩顶的沉降sct可表示为:

式中:sp(0)为桩顶处(z=0)芯桩与水泥土桩的界面相对位移;sc(0)为桩顶处(z=0)水泥土桩与土体界面相对位移;ss(0)为桩顶处土体的压缩量.
在桩底处,芯桩与水泥土桩、水泥土桩与桩周土体界面会产生相对位移,且由于芯桩、水泥土桩和桩周土体的刚度不同,其桩底产生的压缩量不同.根据桩底处的变形关系(见图1),芯桩桩底产生的压缩量spb表示为:

水泥土桩桩底压缩量为scb:

式中:sp(L)为桩底处(z=L)芯桩与水泥土桩的界面相对位移;sc(L)为桩底处(z=L)水泥土桩与土体界面相对位移.
1.2 基本假定
1)假设等芯型水泥土复合桩芯桩与水泥土桩及桩周土均为线弹性体;
2)芯桩-水泥土界面具有剪切软化特性[17],假定水泥土-混凝土界面的荷载传递模型为双指数函数型荷载传递模型[19](见图2(a)),即有:
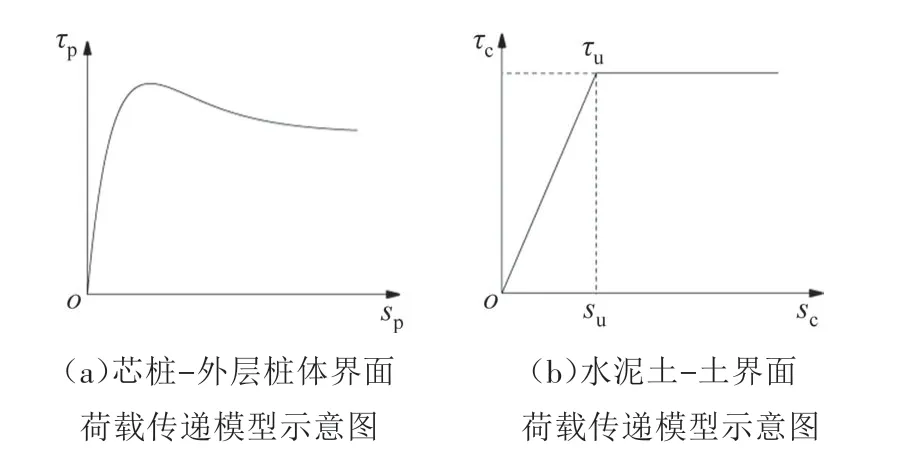
图2 荷载传递模型示意图Fig.2 Schematic for the load transfer models

式中:τp为芯桩-水泥土界面的侧摩阻力;sp为芯桩-水泥土界面的相对位移;a、b、c为模型参数,可通过现场试验结果反演或室内界面试验确定.
3)试验结果[20]与理论研究[13-15]表明,理想弹塑性模型(见图2(b))能够较好地反映水泥土-土界面的荷载传递关系.因此,假定水泥土-土界面的荷载传递模型为理想弹塑性模型,即有:

式中:τc为水泥土-土界面的侧摩阻力;sc为水泥土-土界面的相对位移;su为界面极限弹性位移,与土的性质有关,可通过经验数据综合确定;τu为界面极限侧摩阻力;k为水泥土-土之间的侧摩阻力发挥刚度系数,可根据水泥土-土的直剪试验经验数据进行反算获得,也可根据均质地基中各向同性的弹性抗剪切刚度系数解答进行求解[5]:

式中:Gs为桩周土的剪切模量;rc为桩身半径;rm为影响半径.
4)在桩端处,桩底土体在荷载作用下将发生压缩变形而产生地基抗力,根据其非线性特征,本文假定桩底土抗力模型为双曲线形式,即为:

式中:f为桩底抗力;sb为桩底处相对于土体的压缩量;α、β为与桩底土层性质有关的模型参数,可通过现场载荷试验或地区经验数据综合确定.
1.3 荷载传递分析
1.3.1 计算单元分析
取深度为z处芯桩、水泥土桩的一个单元体(非桩底单元体)进行受力分析(忽略水泥土桩单元体顶面和底面的剪应力的影响),如图3所示.

图3 芯桩和水泥土桩单元体力示意图Fig.3 Stress diagram of the element of core pile and cemented soil
忽略桩体自重,根据单元体静力平衡关系,有:
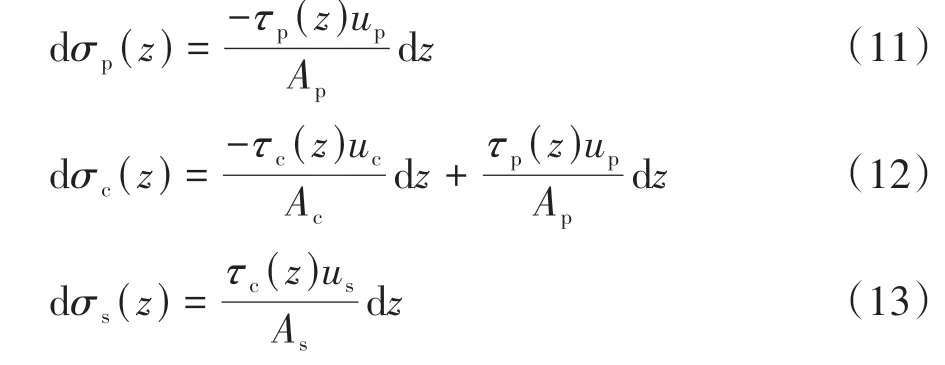
式中:Ap、Ac、As分别为芯桩、水泥土桩和有效处理范围内桩周土的横截面积;up、uc、us分别为芯桩、水泥土桩和桩周土的周长;τp(z)为芯桩-水泥土桩界面在z处的摩阻力;τc(z)为水泥土桩-桩周土界面在z处的摩阻力.
根据图4 所示,芯桩-水泥土界面的相对位移增量dsp为芯桩单元体压缩量与水泥土桩单元体压缩量之差,水泥土-桩周土界面的相对位移增量dsc为水泥土桩单元体压缩量与桩周土单元体压缩量之差,即:

图4 芯桩与水泥土桩界面变形示意图Fig.4 Schematic for the interface deformation mode between core pile and cemented soil

式中:Δp、Δc、Δs分别为芯桩、水泥土桩与桩周土单元体的变形量.
1.3.2 荷载传递关系的建立
将桩长为L的等芯型水泥土桩自下而上分成m个单元体,每个单元体的长度ΔL=L/m,共m+1 个节点.此时桩底(z=L)对应第1 个节点,桩顶(z=0)对应第m+1个节点.
1)当1<i≤m+1时,芯桩与水泥土桩第i个节点与第i+1 个节点之间的轴向应力增量dσp(z)、dσc(z)、dσs(z)分别为:

式中:σp(i)、σc(i)、σs(i)为芯桩、水泥土桩、桩周土在第i个节点处的轴向应力.
将式(11)~(13)代入式(16)~(18),整理得:

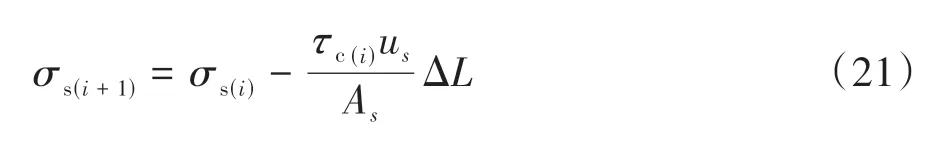
式中:τp(i)、τc(i)分别为芯桩、水泥土桩在第i个节点处的侧摩阻力.
在上部荷载作用下,芯桩-水泥土界面与水泥土-土界面之间的相对位移关系如图4 所示,由式(14)和式(15)可以得到:
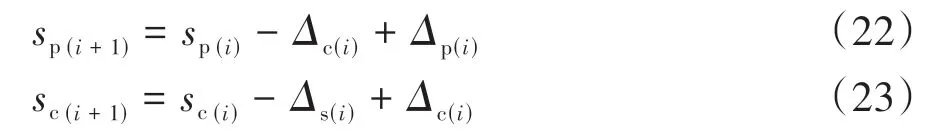
式中:sp(i)、sc(i)分别为芯桩-水泥土桩界面、水泥土-土界面在第i个节点处的相对位移;Δp(i)、Δc(i)、Δs(i)分别为第i个芯桩单元体、水泥土桩单元体、桩周土单元体的变形量.
根据胡克定律,式(22)(23)整理得:

将界面相对位移sp(i+1)、sc(i+1)代入式(7)与式(8),即可得到第i+1 节点处芯桩-水泥土界面与水泥土-土界面的桩侧摩阻力τp(i+1)、τc(i+1).
2)当i=1 时(桩底单元),若已知桩底的位移边界条件,便可根据式(10)得到桩底处的受力,根据荷载传递函数式(7)和式(8),得到桩底处侧摩阻力值,进而往上逐个递推求出m+1 个节点的应力、侧摩阻力与相对位移.
以上建立了劲芯水泥土复合桩的荷载传递关系,由于问题的复杂性,难以用解析的方法进行求解.因此,下面将采用迭代计算方法确定劲芯和水泥土桩的轴力、侧摩阻力以及界面相对位移沿桩体分布,进一步获得荷载-沉降曲线,由此确定劲芯水泥土复合桩的承载力.
1.4 迭代求解
本文通过迭代求解的计算方法对劲芯水泥土复合桩轴力、侧摩阻力、界面相对位移沿桩长的分布规律进行计算.由于桩体的极限承载力未知,若按荷载进行加载可能超出其承载力范围,故本文采用按位移控制的方式进行加载.求解的总体思路为,首先给定一个等芯型水泥土桩的桩底总位移sb〔sb=sp(L)+sc(L)+ss(L)〕,并任意选取各相对位移的值〔ss(L)、sc(L)〕,然后由桩的荷载传递关系递推计算出该位移边界条件下轴向应力、侧摩阻力、相对位移沿桩身的分布,再以桩顶的应力比为条件判定相对位移取值的合理性,并通过迭代循环确定合理取值,最后得到该总位移对应的荷载传递特性计算结果.
具体求解步骤和计算流程如下:
1)将芯桩、水泥土桩、桩周土离散为m个等长的单元体(共m+1 个节点),单元体长度为ΔL=L/m,由桩底第1个节点开始对每个单元体进行递推分析.
2)采用按位移控制的方法进行加载,给定一个芯桩底绝对位移sb.

5)由式(10)计算芯桩、水泥土桩、桩周土在第1个节点的轴向应力.
6)由式(7)与式(8)计算芯桩、水泥土桩第1 个节点(即桩底处)的侧摩阻力.
7)由式(19)~(21)、式(24)~(26)、式(7)(8)逐个节点向上迭代计算,对整根桩m+1 个节点的轴向应力、侧摩阻力、相对位移进行求解.


10)给定不同的桩底沉降sb,重复步骤2)~9),计算出不同上部荷载作用下,芯桩以及水泥土桩的轴向应力、侧摩阻力、界面相对位移沿桩长的分布.
11)根据Pp(z)=Apσp(z)、Pc(z)=Acσc(z),计算出相应的轴力沿桩身的分布,并得到桩的荷载-位移曲线(P-s曲线).
基于MATLAB 对上述柔性基础下等芯型水泥土复合桩计算方法编制了相应的计算程序.在实际工程设计计算中,先通过试验或相关资料获得劲芯水泥土复合桩的几何参数、桩与土的弹性模量、内外界面的荷载传递模型参数、桩底抗力模型参数和桩顶应力比,再利用本文编制的计算程序可很便捷地求解出芯桩和水泥土桩的轴力、侧摩阻力分布,进而可计算得到劲芯水泥土复合桩的荷载P-沉降s曲线.
2 现场足尺试验结果验证分析
为验证本文方法的可靠性,采用李进军[21]通过足尺搅拌桩现场静载荷试验得到的试验结果来进行验证分析.该等芯型水泥土复合桩桩径D=600 mm,桩长L=14 m,芯桩为钢筋混凝土等截面方桩,截面尺寸为270 mm×270 mm,芯桩桩体的弹性模量Ep=4.2×104MPa,水泥土弹性模量Ec=150 MPa.加载时荷载作用在芯桩顶部.对于水泥土-混凝土界面的荷载传递函数模型的参数取值,根据文献[22-23]的试验数据反算可以得到a的取值范围为110~700 kPa,b的取值范围为0.08~0.23 mm-1,c的取值范围为40~110 kPa.以此作为参考范围,取a=200 kPa,b=0.15 mm-1,c=110 kPa.水泥土-土界面荷载传递的参数取值,以王忍[20]的水泥土桩-土摩擦特性的多组试验研究结果作为参考范围,取k=20 kPa/mm,τu=65 kPa;桩底地基抗力模型参数取值为,α=9×10-3mm/kPa,β=3.5×10-3kPa-1.根据上述参数,用本文提出的方法对劲芯水泥土复合桩的荷载传递规律进行了分析,以芯桩桩顶沉降为总沉降,将试验结果与本文方法计算结果进行对比,绘于图5.
图5 表明,本文方法计算结果与试验结果均具有较高的吻合度.两种方法所得的极限承载力均为1 840 kN.桩顶沉降量的计算值与实测值的平均绝对误差为0.384 mm,平均相对误差为11.7%,由此证明本文提出的计算方法是合理可靠的.
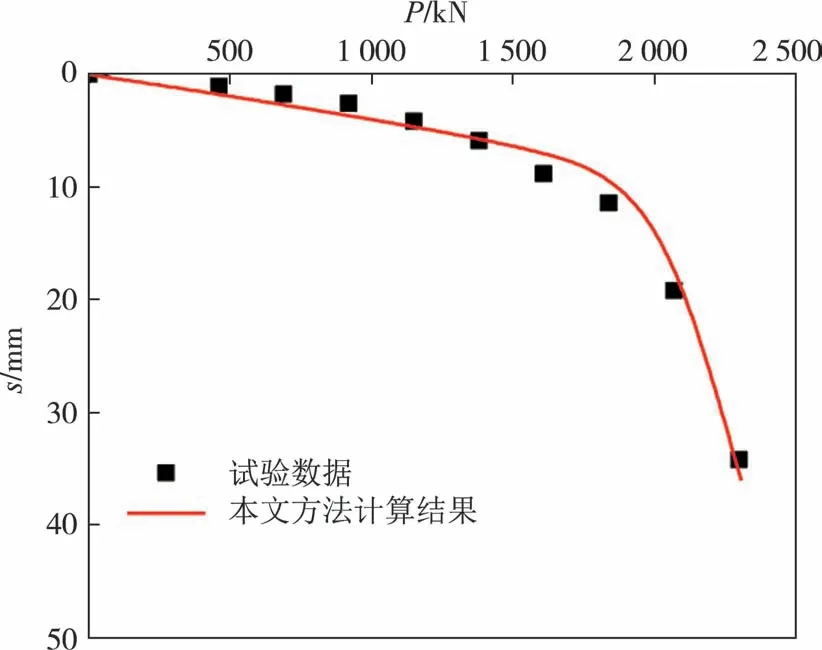
图5 复合桩现场试验P-s曲线的实测值与理论计算值对比(案例1)Fig.5 Comparison between measwrements and the theoretical calculations of the P-s curve in field test for composite pile(Case 1)
3 工程案例对比验证及荷载传递规律分析
3.1 案例验证
为进一步验证本文方法的可靠性,以山东某工程劲芯水泥土桩[24]复合地基静载荷试验数据进行对比验证.该等芯型水泥土桩直径D=800 mm,芯桩直径d=400 mm,桩长L=12 m,芯桩桩体的弹性模量Ep=3.8×104MPa,水泥土弹性模量Ec=400 MPa,桩周土为粉土与粉质黏土,计算中简化为均质土,取弹性模量Es=25 MPa.根据文献[22-23]与课题组开展的水泥土-筋体界面剪切试验数据[25],取a=600 kPa,b=0.15 mm-1,c=120 kPa;k=40 kPa/mm,τu=80 kPa.桩底土为粉砂,取α=0.1×10-3mm/kPa,β=0.3×10-3kPa-1.根据文献[24]的试验结果,取npc=21∶1,ncs=3.45∶1.将本文方法分析计算结果与实测数据结果进行对比,见图6.可以看出,本文计算结果与实测结果吻合度较高,进一步证明了本文的计算方法可靠.
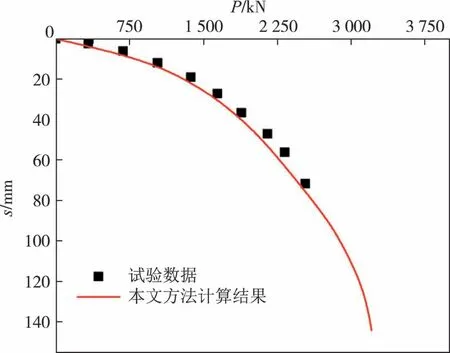
图6 复合桩现场试验P-s曲线的实测值与理论计算值对比(案例2)Fig.6 Comparison between measwrements and the theoretical calculations of the P-s curve in field test for composite pile(Case 2)
3.2 荷载传递规律分析
下面以3.1节工程案例为例,采用本文方法对该等芯型水泥土复合桩芯桩与水泥土桩的轴力、侧摩阻力进行求解,对其轴力、侧摩阻力分布规律进行分析.
3.2.1 桩侧摩阻力分布规律分析
不同于刚性基础下等芯型水泥土复合桩的侧摩阻力分布[6],柔性基础下的等芯型水泥土复合桩的芯桩-水泥土界面与水泥土-桩周土界面的侧摩阻力均存在负值,这是柔性基础下桩顶处芯桩、水泥土桩和土体的差异沉降引起的.对于桩顶处芯桩-水泥土桩界面,因芯桩的刚度较大,水泥土桩相对于芯桩产生向下的相对位移从而产生负侧摩阻力.同理,对于桩顶处水泥土桩-桩周土界面,水泥土桩的刚度大于土体,水泥土桩则会刺入垫层,从而产生负侧摩阻力.而在桩底处,因芯桩和水泥土桩受到土体抗力作用,芯桩-水泥土界面和水泥土-桩周土界面将产生正向的相对位移与侧摩阻力.于是,在桩身某深度处将出现界面相对位移等于0 的现象,该位置即等沉面.由图7、图8可知,芯桩与水泥土桩的等沉面位于桩身上半段,即0~6 m的范围,此外,等沉面的位置随上部荷载增加而上移.
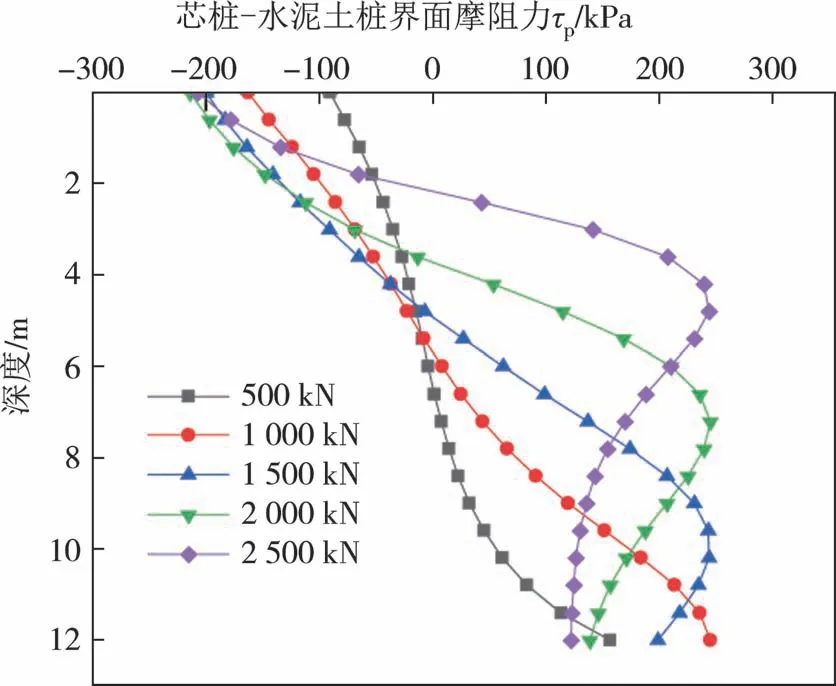
图7 芯桩侧摩阻力分布图Fig.7 Distribution of side friction resistance of core pile
对于本文案例,由图7 可知,荷载P≤1 000 kN时,芯桩侧摩阻力的代数值沿深度递增,此时芯桩-水泥土桩界面尚未进入塑性阶段;当P≥1 500 kN 时,芯桩-水泥土桩界面自桩底开始部分范围进入塑性阶段,侧摩阻力分布出现峰值,软化段范围随上部荷载的增加而扩大.而对于水泥土桩,由图8 可知,桩顶会首先进入塑性阶段,随着荷载的增加,塑性区范围不断扩大,最终,桩底也会进入塑性阶段.整体而言,芯桩-水泥土桩界面的塑性区范围大于水泥土桩-桩周土界面.

图8 水泥土桩侧摩阻力分布图Fig.8 Distribution of side friction resistance of cemented soil
3.2.2 桩身轴力分布规律分析
图9、图10 所示分别为劲芯水泥土复合桩芯桩与水泥土桩的轴力沿桩身的分布.

图9 芯桩轴力分布Fig.9 Axial force distribution of core pile

图10 水泥土桩轴力分布Fig.10 Axial force distribution of cemented soil
由图9 可知,芯桩的轴力沿深度先递增后递减.不同荷载下芯桩桩底的轴力值相近,这是由于桩底处芯桩刺入土体较多,已达到桩底抗力极限值.结合图7,在等沉面以上,由于受到负的侧摩阻力作用,芯桩轴力沿深度增加;而在等沉面以下,芯桩承担的荷载逐渐通过侧摩阻力传递给水泥土桩,轴力沿深度递减.
由图10 可知,当荷载P≤1 500 kN 时,水泥土桩轴力沿深度先递减后递增;当荷载P≥2 000 kN 时,水泥土桩轴力沿深度先递减后递增再递减,其分布大致呈“S”形.此外,水泥土桩在桩底处的轴力约为桩顶处轴力的2.2~2.5 倍.水泥土桩外侧在等沉面以上受土体向下的侧摩阻力,内侧受到芯桩向上的侧摩阻力;等沉面以下部分,侧摩阻力的方向恰好相反.因此,水泥土桩轴力分布受内外界面侧摩阻力综合的影响.
4 结 论
1)劲芯水泥土复合桩在柔性和刚性基础下的受力变形模式截然不同.柔性基础下劲芯水泥土复合桩在桩顶处将不同程度地刺入垫层,它不再满足等应变假设,不能简单地套用刚性基础下劲芯水泥土复合桩计算方法进行计算分析.
2)本文通过分析柔性基础下等芯型水泥土复合桩的变形与受力模式,基于荷载传递法,结合迭代计算,提出了一种柔性基础作用下等芯型水泥土复合桩的荷载传递规律的分析计算方法,编制了相应的计算程序,可高效、便捷地用于实际工程,计算出芯桩、水泥土桩的侧摩阻力、轴力分布,并绘制出劲芯水泥土复合桩桩顶的荷载-沉降曲线.
3)采用本文方法对等芯型水泥土复合桩工程案例进行分析计算,得到了P-s曲线与极限承载力.计算结果与实测数据曲线吻合良好,证明了本文方法的可靠性.
4)柔性基础下的等芯型水泥土复合桩的荷载传递特性与刚性基础下的荷载传递特性存在较大的区别:桩顶产生差异沉降,芯桩与水泥土桩在桩顶处有负摩阻力段;桩身存在一个等沉面,等沉面位于桩身的上半段,等沉面随上部荷载增加而上移;芯桩桩身轴力沿深度先递减后递增;水泥土桩轴力总体表现为沿深度先递减后递增.

