松散岩堆细-宏观强度关系与围岩压力
陈志敏 ,刘耀辉 ,郭利民 ,李宁 ,王壹敏
(1.兰州交通大学 土木工程学院,甘肃 兰州 730070;2.中铁第一勘察设计院集团有限公司,陕西 西安 710043;3.道桥工程灾害防治技术国家地方联合工程实验室(兰州交通大学),甘肃 兰州 730070)
受青藏高原构造运动影响,中国西南某高海拔地交界地带山高谷深且地质运动活跃,为大孔隙率松散岩堆的形成创造了合适的自然条件.
松散岩堆是岩块与土体的混合岩土体,岩块和土颗粒的混合特征与松散岩堆的形成条件有直接关系,岩块堆积具有一定特征,堆积体存在时间越短,其架空越明显,土体填充越少,岩堆越松散[1-3].国内外学者对此类大孔隙率松散岩堆做了许多试验研究.Vallejo 等[4]研究了砂石-黏土混合材料的不同含量对抗剪强度影响;龚超凡等[5]研究了试样高度对粗颗粒土抗剪强度的影响;荀晓慧等[6]根据能量守恒原理和Mohr-Coulomb 强度准则,推导了能量演化与强度参数的关系等;对于密实硬岩岩堆,压实度主要取决于岩块间的摩擦阻力,岩块压碎引起的变形量很小;内摩擦角随周围压力的增大呈非线性,压实硬岩岩堆的应力-应变关系近似弹性应变软化型[7-9].上述研究都是基于连续介质力学假定进行宏观层面的物理力学性质研究.岩块单元相对隧道洞室的大小程度使得其既不能应用岩石力学的方法,也不能应用经典土力学方法解决围岩稳定问题.松散岩堆与一般岩土体的最大区别在于其相对大小和非连续性,不符合以上两种方法的连续均匀性假设.
经典土力学解决了大量实际问题,为注重机理研究的颗粒材料力学提供了验证依据,并指导颗粒材料力学的研究更加接近实际工程,因此土力学与颗粒材料力学有紧密的联系,无黏性砂土的剪胀性研究更是促进了岩土颗粒力学的发展[10-11].例如:有效应力可以用土颗粒的浮力定律来解释,达西渗流定律可以解释为岩土颗粒间的孔隙流体平衡和颗粒骨架对流体的阻力作用的综合描述,进一步有饱和土力学的孔压系数的微观解释以及岩土本身的微观结构都蕴含着深刻而严格的颗粒材料力学问题.随着土力学的发展,土力学研究者越来越重视岩土微观结构作用.宏-微观参数对应关系是颗粒力学的一个基本问题,土体微观结构测试[12]、颗粒间接触测试[13]及DEM 模型[14]更是推动了土体宏微观研究的发展.常在[15]、刘海涛等[16]研究了砂土宏观抗剪强度与颗粒间摩擦强度之间的相似关系;巩师林等[17]改进了DDA 计算方法中的块体变形问题;康馨等[18]引入修正的三维形状系数S,研究了不同砂颗粒对其相关物理量的影响;曹文贵等[19]探讨了在空隙变化影响下岩石微观应力和变形与其宏观应力和变形之间的关系;蔡国庆等[20]依托PFC3D 中的黏结模型建立了非饱和土体颗粒间黏结强度的宏-细观关系.上述研究多是从宏-微观角度研究土体的强度特性,对于松散岩块的局部强度研究仍有不足.与传统土力学材料不同的是,松散岩堆在破坏时与其荷载方向有很大关系.岩块材料通过接触力链,少数颗粒承担了大部分力;在纯剪和双向压缩状态下,接触力方向差异较大[21-22].因此松散岩堆局部强度对工程而言同样有重要意义.颗粒粒径和试样尺寸不同时,强度相差很大,若岩堆材料数量足够大,则宏观峰值强度趋于稳定[23-24],而局部强度特征不能体现.
松散岩堆是典型的颗粒材料,在隧道进口和出洞段的松散岩堆的围岩变形问题目前仍是隧道工程中一个尚未明确的重要问题.为了研究松散岩堆的强度和围岩稳定,本文从颗粒材料力学对致密砂土的力学分析出发,来研究松散岩堆的细观岩块单元与宏观强度的密切关系.
1 松散岩堆细观咬合关系模型
1.1 经典应力剪胀关系
Rowe[11]在20 世纪60 年代提出了颗粒材料的应力剪胀关系,并提出了滑裂面的剪切滑移分析模型.模型建立在密实砂土三轴试验状态的基础上,模型假设试样为两块刚性楔块,楔块沿剪切面发生滑移,滑移面与最小主应力σ3方向夹角为α,而颗粒材料的滑移面在咬合作用下呈现锯齿状,锯齿面p与最大主应力σ1方向夹角为β.
Rowe 认为锯齿面相互滑动过程中体积增大,可以解释颗粒材料的剪胀性,如图1 所示.继而通过平衡条件和变形协调条件得出了应力剪胀关系式,见式(1).

图1 Rowe剪切滑移分析模型Fig.1 Rowe shear slip analysis model

式中:σ1和σ3分别为最大和最小主应力;εv和ε1分别为体积应变和轴向应变;φµ是颗粒间摩擦角.
Rowe根据最小能比原则,得到:

从而得到Rowe应力剪胀关系:

该公式在颗粒材料密实状态下吻合较好,松散状态时,Rowe进行了修正,用松散颗粒材料摩擦角φf代替φµ(φµ≤φf≤φcv),φcv是三轴试验中的临界摩擦角.
随后,Josselin[25]利用摩擦定律对Rowe采用的最小能比原理进行了证明,其力学模型如图2 所示.模型中α是下锯齿面与最小主应力方向的夹角,β是上锯齿面与最大主应力方向的夹角,θ为锯齿面和滑移面的夹角,它们三者有着一定的关系,即θ=α+β-π/2,n为锯齿面的法线方向,F为锯齿面上的作用合力,ω为力F与法线方向n的夹角.

图2 Josselin剪切滑移分析模型Fig.2 Josselin shear slip analysis model
上述模型假设的前提是都存在锯齿状剪切滑移平面,且发生了剪胀.大量颗粒材料三轴试验表明,在密实状态下该应力剪胀关系公式与应力应变关系有很好的契合度,但在解释松散颗粒材料状态下的应力应变关系时较为困难.松散颗粒材料的三轴试验变形破坏结果并非存在锯齿状滑移平面,松散状态下留有较大的孔隙率可以有效地缓解或者抵消剪胀作用,松散颗粒材料更容易发生局部应力应变.基于此,要进一步研究大孔隙率松散岩堆强度关系则需进一步建立细观模型.
1.2 松散岩堆细观咬合关系模型建立
松散岩堆有一定的宽泛的颗粒级配,一般只受到重力荷载的堆积作用,其密实度较小,而且有较大的孔隙率,在隧道工程中的围岩力学行为主要是由于卸载引起的,与应力剪胀关系有所区别,因此其细观的咬合作用有待进一步分析研究.
此外,上述应力剪胀关系中的体积应变与轴向应变在实际工程中现场测量较为困难.松散岩堆粒径较大,开展现场试验较为困难,通过运用土力学和颗粒材料力学来研究松散岩堆细观岩块单元间的力学机制与宏观强度的关系是一个较好的解决办法.通过较为简单的物理力学参数来得到松散岩堆的强度,从而方便实际工程中的运用.
松散岩堆主要受自重应力影响,结构较细粒土更加简单,其破坏过程主要是堆积单元岩块的物理运动.假设松散岩堆的破坏过程没有单个岩块的挤压碎裂,可以简单地认为,每个基本岩块单元为刚体,松散岩堆在类弹性阶段的强度主要依靠岩块单元的咬合作用,而岩块单元间的咬合主要是来源于特殊的摩擦机制.
松散岩堆有着非线性特征和应力应变局部化、跨越固体和液体的类固-液转变行为.与颗粒力学有所区别的是,松散岩堆是一种宏观的力学行为,松散岩堆变形有着不可逆性.在上面模型的基础上,建立细观状态下的松散岩堆的平面咬合模型,如图3所示.

图3 咬合作用示意图Fig.3 Schematic diagram of occlusion
由于大部分自然形成的岩块表面往往是坑洼不平的,其接触必定是较小面积与较大面积间的接触,为了突出该特点,松散岩堆的变形模式是点-面接触作用,以某一岩块作为绝对静止的对象,和它咬合的其他两块岩块作相对运动,其运动轨迹是点-面接触模式下,沿岩块单元接触面的滑移和以点为圆心的转动.在接触变形的情况下,变形之前,岩块滑移面与竖向夹角为β,发生小变形后,岩块发生滑移面偏移,由于岩块相对旋转偏移角度为θ,滑移面与水平方向夹角为α,它们三者之间满足下列关系:

2 松散岩堆咬合关系与宏观强度规律的关系
接触点合力方向与滑移面法线方向成夹角ω,而岩块单元间的摩擦角设为φµ,依据摩擦定律有:
当ω<φµ时,两岩块单元有滑动趋势,但不会发生相对滑动;
当ω=φµ时,两岩块单元间滑动趋势达到滑动摩擦力,可以发生相对滑动;
当ω>φµ时,在松散岩堆破坏形式下,认为岩堆内部岩块单元运动速度很小,不考虑加速度,两岩块单元间的合力超过最大滑动摩擦力,这种情况不会出现.
同样地,依然假设松散岩堆受力状态为三轴应力状态,内部岩块单元咬合机理如图3 所示,在笛卡儿坐标系下进行方向标定,以竖向或轴向为y轴,而x轴和z轴构成水平的平面坐标,岩堆三轴试样在x、y、z方向上的有效应力分别可以表示为σ′1、σ′2、σ′3,并且三轴状态下应力关系为σ′1>σ′2=σ′3.
在对松散岩堆体相似材料做三轴试验之后发现,松散岩堆变形以鼓状变形为主,其变形如图4 所示.之所以出现膨胀变形是由于较大的孔隙率提供了轴向压缩变形空间,在松散岩堆压缩变形的同时,由于咬合作用产生围向膨胀变形,在这个过程中岩块单元间的咬合作用主要来源是特殊机制下的摩擦力,对于摩擦因数基本一致的松散岩堆,可以认为内部岩块单元间的接触力大小相等.上述模型中假设在松散岩堆发生变形时,水平方向约束条件不变,岩块单元间合力方向与水平方向夹角为ω+β,由图3中关系可得到:

图4 岩堆相似材料三轴试验试样变形特征Fig.4 Deformation characteristics of triaxial test specimens of similar materials in rock piles

式中:Fy′为岩块单元间作用力的竖向分力;Fx′为岩块单元间作用力的水平方向分力.
松散岩堆咬合作用下的变形,主要是岩块单元的相对平动和转动,这两种方式都可以占据主导地位,主要取决于岩块单元间的摩擦因数和比密实度.但无论哪种方式占据主导,松散岩堆剪胀效应的实质是由宏观状态下轴向和横向变形引起的,因此在松散状态下岩块单元相对转动引起的体积变化,可以转化为岩块单元间接触面上的位移.
无论是平移,还是转动,对于某个岩块单元来说位移是由于和其配位接触的其他岩块单元相互作用引起的,因此它的运动是协调的,沿着点-面接触相对滑动一段极小位移Δu′则可以代表这个岩块单元的剪胀变形量,uy′是岩块单元的竖向相对位移,ux′是岩块单元水平方向相对位移,满足矢量关系:

由上述的几何关系可以得到:

岩块单元在外力作用条件下消耗一定能量,主要消耗对象是岩块单元间的摩擦作用.由于岩土体的变形可以认为是缓慢的或者静止的,因此忽略岩块单元的滑动动量和转动惯量条件下,定义轴向和横向变形所消耗的能量比为:

由式(8)可知,能量比E随着ω的增大而增大,随着β的增大而减小.能量比E可以通过宏观的外力做功获取,而岩堆内部岩块单元间滑移面与竖向夹角β,由于各个岩块单元间咬合过程中的滑移面角度不同,可以看作自变量.而在一定的外界荷载和约束条件下,接触点合力方向与水平方向所成夹角为ω+β,因此ω可作为因变量,进而得到:
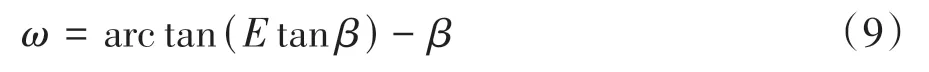
对式(9)求导,利用ω最大值条件∂ω/∂β=0,来求得所对应自变量β的值:

利用三角函数倍角变换以及β、ω的值域得:

进一步对两者关系进行分析,对原式求二阶导数,将该值代入得到:

由此可知,该值是一个极大值.ω的值域为(0,φµ).当岩堆发生变形时,内部岩块单元间ω达到最大值;当ω+β为一个定值时,β越大则能量比E越小.由上述求导可知,ω是关于β的增函数,由此可知当ω=φµ作为极大值时,β也最大,因此能量比E也越小,因此得到:

实际工程中,岩块单元间通常不是严格意义上的点-面的接触,还需要考虑到接触面积ΔA,Ax′和Ay′分别是横向和竖向的接触面积,根据几何关系,可以得到:

根据应力和力的关系,将接触面积比代入,可以得到岩块单元间接触极限应力比值,若将松散岩堆三轴应力状态下的荷载在岩堆内部平均化,则可以得到细观咬合模型同宏观外荷载的关系:

值得一提的是,这里的外荷载与岩堆内部应力并不是相等关系,还与岩块单元的孔隙率和实际接触面积等有关.然而可以简单地认为,竖向和横向的内部结构一致,因此外荷载与岩堆内部应力比值大小是相等的.由式(15)可知,松散岩堆细观摩擦角对宏观强度有较大影响.
3 松散岩堆隧道围岩力学分析
3.1 普氏理论松散岩堆围岩应力拱
围岩压力的确定对隧道设计和围岩稳定性分析有重要意义,围岩压力可以通过直接测量、经验、理论估算等方法确定.较早的理论只考虑单因素下的围岩压力计算,主要有普氏理论和应力传递法等,随后出现了双指标分级、巴顿岩体质量(Q)分级、BQ 分级法、专家系统法和模糊信息评价法等多因素围岩压力计算方法,目前我国的围岩压力计算方法是根据以BQ分级法为基础的经验法制定的.
松散岩堆可看作是岩体破坏后的坡体或者以堆积体形式存在的,自然堆积形成一定高度,除重力场方向的地基承载力以外,必须有一定的侧向约束,才能保证其具有一定高度.岩堆内部接触力链不是竖向传递的,而是水平力和竖向力的合力.假设地基是绝对光滑地面,岩堆则不会形成坡体.为方便研究,假定岩堆接触力链构成平面力链网,可以得到滑移面网格分布如图5 所示,力链网的拐点是虚构的,是假设岩块单元的平面配位数为4,通过延伸滑移面得到的.
松散岩堆在小变形阶段保持稳定状态,也就是应力应变曲线类弹性变化阶段.滑移面、岩块在点-面接触下的内部应力路径等如图5 所示,将咬合模型中的各岩块单元的滑移面延伸相交,组成网格,各网格内部代表不同形状的岩块单元.当岩块单元间达到其最大摩擦角ω=φµ时,岩块单元间发生的位移很小,滑移面角度β=π/4-φµ/2,咬合作用的偏转角θ=0,那么由式θ=α+β-π/2,可得滑移面与最小主应力的夹角α为:


图5 松散岩堆滑移面网格分布Fig.5 Grid distribution of slip surface of loose rock pile
当隧道开挖后,岩堆内部发生应力重分布,一定范围内的岩块单元沿临空面产生位移,形成松弛.由于侧向边界约束的作用,形成一定的拱效应.当满足式(16)时,围岩可以形成自稳的应力拱.
为了求得自稳的应力拱高度内的围岩压力,必须确定隧道洞顶到应力拱线的最大距离h.以自然平衡拱轴线的顶端为坐标原点,建立笛卡儿坐标系,水平向左为x轴正方向,竖直向下为y轴正方向,自然平衡拱轴线图如图6所示.
应力拱轴线拱脚处松散岩堆应满足深度条件:

式中:γ为松散岩堆宏观重度;H为平衡应力拱拱脚处埋深;T为应力拱轴线拱顶处水平推力.
拱轴线与原点相交,在原点o(0,0)处取一微段,从细观角度分析如图7 所示.普氏理论将计算模型简化,认为竖向压力q是拱轴线上部岩体的自重所产生的均布荷载,且图7 实质上是图6 拱轴线上的微段,当x方向上取一微段dx时,拱轴线上对应为m点,m点弯矩应为均布荷载的合力G乘合力作用点到m点的距离(y=dy时所对应的dx的一半).拱轴线是围岩是否塌落的分界线,故在拱轴线上岩体不能承受拉应力,当y=dy时,竖向荷载G和水平推力t到拱轴线上m点的弯矩作用差值应为0,从而得到式(18).
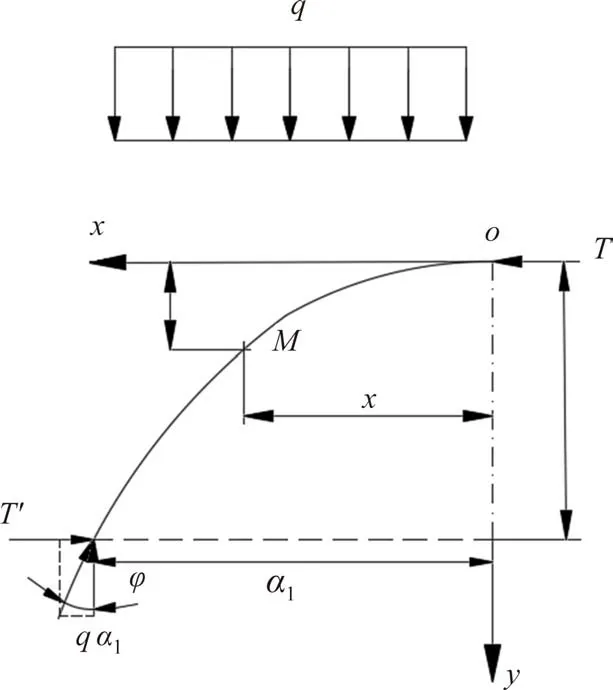
图6 自然平衡拱计算图Fig.6 Calculation diagram of natural balance arch

图7 拱轴线微分示意图Fig.7 Differential schematic diagram of arch axis

式中:G为微段拱轴线上部岩体的自重荷载,即G=qa;t为平衡应力拱拱顶截面的水平推力;dx、dy分别为o点的x、y轴增量值.
在拱轴线任意点处,该微段受外荷载作用可看作是与三轴应力状态一致,则根据松散岩堆宏观外荷载与细观咬合强度关系可得:

由式(18)和式(19)可得到y轴的增量dy与松散岩堆细观强度关系为:

求解式(20)所示微分方程即可得到应力拱轴线在笛卡儿坐标下的解析式:

式中:C为常数,受多种因素影响,主要与松散岩堆的岩块单元与隧道洞径的比值、岩堆体内摩擦角φµ有关,粒径小至一定值时,所需最大高度y为无限大.
由式(21)可知,自然平衡拱轴线为二次抛物线,其应力平衡条件为二次项,应力拱高度与咬合强度关系呈正相关.
当应力拱的跨度达到a1时,即可得到隧道洞顶到应力拱线的最大距离h为:

式中:a1为应力拱轴线的计算水平距离,可由α与隧道断面高度Ht的三角函数关系得到:

3.2 基于细-宏观强度关系的松散岩堆围岩压力
普氏理论认为:作用在硐室顶部的围岩压力仅为拱内岩体的自重.但普氏理论仅仅是在宏观层面给出了围岩压力的计算方法,而对于松散岩堆体隧道,洞顶所受围岩压力应考虑岩堆体细-宏观强度关系,因此认为对于硐室顶部的围岩压力仍然可以用普氏理论去计算,但需对其做出修正,隧道所受围岩压力示意图如图8 所示.结合松散岩堆细观咬合模型与宏观外荷载之间的关系,由式(15)和式(22)即可得到大孔隙率巨型松散岩堆体考虑了细-宏观强度关系的围岩压力计算公式如式(24)所示.
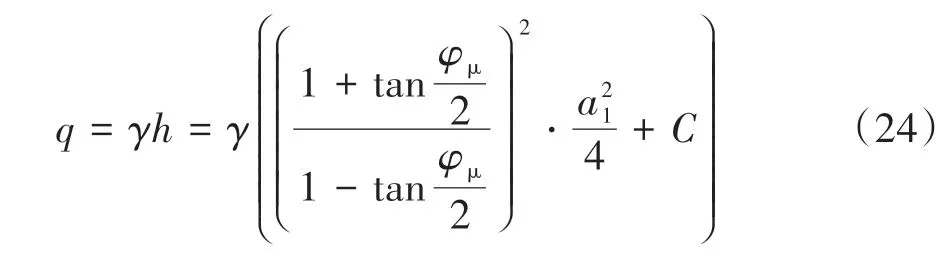

图8 松散岩堆隧道细-宏观围岩压力示例图Fig.8 Example diagram of fine-macroscopic surrounding rock pressure of loose rock pile tunnel
隧道硐室的侧向围岩压力,同样考虑松散岩堆体的咬合作用机制及细-宏观强度关系,因此同样对宏观层面普氏围岩侧向压力理论值做出修正:

联立式(15)(16)(22)(25)(26)可得松散岩堆隧道硐室侧向围岩压力:

由此可见,松散岩堆体隧道的围岩压力无论是竖向压力还是侧向压力与咬合强度的关系均为正相关,围岩压力均受到应力拱轴线的计算水平距离a1与岩块单元间的摩擦角φµ的共同影响.
3.3 松散岩堆隧道围岩压力计算实例
中国西南某铁路隧道进出口段分布有较大规模的岩堆体,主要以碎石为主,厚度10~50 m 不等,块径多介于0.5~2 m,最大块径达到5 m,在自然状态下稳定性较好.岩堆对隧道主体工程影响较大,施工会影响岩堆的稳定性,存在局部失稳风险.依托该隧道工程建设,采用修正的细-宏观普氏理论围岩压力计算公式,对隧道围岩压力进行计算,并与太沙基理论围岩压力及《铁路隧道设计规范》(TB 10003—2016)[26](以下简称规范)围岩压力计算结果对比,计算中各参数取值见表1,围岩压力计算结果见表2.其中,在太沙基理论计算中采用朗金公式计算其侧向围岩压力,常数C的取值可参考如式(29)所示经验公式计算,但后续仍需大量数据进行修正:

表1 中国西南某铁路隧道围岩压力计算参数表Tab.1 Calculation parameters of surrounding rock pressure of a railway tunnel in southwest China

式中:d为岩体粒径,m.
为方便对比,考虑到普氏理论及规范算法中侧向围岩压力均呈线性变化,因此取平均值与其余结果比较.由表2 可知:修正后的普氏理论比一般普氏理论计算结果大,差值约28 kPa,局部强度对整体围岩压力的影响不可忽略,说明本文所提出的计算公式是合理的、可应用的,但由于普氏系数的计算有人为经验因素影响,修正后的普氏理论则严格受到内摩擦角及滑移面与水平面夹角α的影响,更为科学严谨;修正的普氏理论在竖向围岩压力计算中比太沙基理论和规范方法略大,除规范深埋算法的结果之外,差值均在30 kPa 以内,这是由于太沙基理论和规范算法中仅仅是将竖向围岩压力在宏观上整体简化为均布荷载,并没有考虑到岩体内部由于相互咬合而造成的细观局部强度带来的影响,而修正的普氏理论将岩体各部分细观局部强度同样用宏观角度均布作用于硐室上方.值得注意的是,规范算法中无限埋深计算方法计算结果出现较大误差,这是由于规范算法在计算过程中仅仅是考虑到硐室上方围岩的自重,忽略了滑移面造成隧道跨度增大的影响,故该方法计算竖向压力结果明显小于其余两种方法,使得其侧向围岩压力同样偏小.对比侧向围岩压力后发现,修正普氏理论计算结果均与其余两种方法有较大差距,差值在80 kPa 左右.究其原因,认为:算例围岩是巨型大孔隙率松散岩堆体,其咬合模型为点-面接触,在受到荷载作用后,岩堆岩块内部产生位移使得其找到新的平衡位置,使得岩块间接触更为紧扣,造成部分围岩压力向围岩方向传递,从而使硐室侧向围岩压力减小.
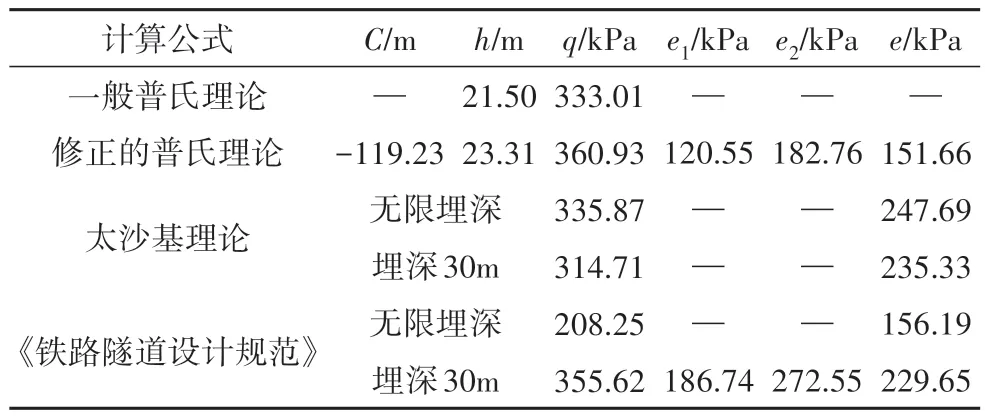
表2 中国西南某铁路隧道围岩压力对照表Tab.2 Comparison table of surrounding rock pressure of a railway tunnel in southwest China
综上所述,基于细-宏观强度修正的普氏理论围岩压力公式更适用于有较大埋深的松散岩体隧道.
4 结论与展望
本文从致密砂的应力剪胀关系式出发,通过分析得出了松散岩堆的细观咬合模型,推导出由岩堆内部岩块单元的摩擦角主导的宏观强度关系式.从适合破碎围岩的普氏理论出发,结合岩堆细观强度公式,得出了松散岩堆自然平衡拱轴线的计算方法,从而从细-宏观角度修正了围岩压力计算公式.主要结论如下:
1)松散岩堆接触模式为点-面接触,其运动轨迹是沿接触面的滑移和以点为圆心的转动;岩块内摩擦角对宏观强度有重要影响,内摩擦角越大,宏观强度越高.
2)应力拱轴线高度h受细-宏观强度关系σ′1/σ′3与滑移面与水平面夹角α共同影响,岩堆细观局部强度对整体围岩压力的影响不可忽略.
3)针对松散岩堆细-宏观力学特性,对普氏理论进行了修正.中国西南某铁路隧道计算结果表明,修正普氏理论结果稍大,体现了松散岩堆隧道的细-宏观力学特性,表明了修正普氏理论的可行性与实用性.
4)修正的围岩压力公式更适用于有较大埋深的松散围岩隧道.后续研究重点将是运用大量数据修正常数C的拟合函数以及在普氏理论计算模型推导过程中求m点弯矩时力臂的取值问题,普氏理论模型仍有待继续修正、细化.

