岩质反倾边坡复合倾倒破坏分析

孙朝燚，陈从新，郑允†，张伟，马力，张海娜，张亚鹏

（1. 中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉430071；2. 中国科学院大学，北京100049）

倾倒破坏是岩质反倾边坡的主要失稳模式之一，常见于露天采矿、水利水电、公路铁路等各类工程边坡中，这些边坡的失稳给工程建设和人民生活造成了严重的危害[1-6].Goodman 和Bray[7]从单个岩层破坏的力学机制出发，将倾倒破坏分为弯曲倾倒、块状倾倒和块状-弯曲复合倾倒三种类型.若岩质边坡中存在一组与边坡走向近似、插入坡内的主控裂隙组如层理、页理等，边坡类似叠合悬臂梁，由于重力作用，岩块承受着拉伸和压缩弯曲应力，当每个岩块中的拉应力超过岩块的抗拉强度时，边坡就会发生倾倒失稳破坏，这种破坏模式称为弯曲倾倒破坏.若上述边坡中还存在一组与主控裂隙组成大角度相交的横向裂隙组，此时岩块不抗拉，由于重力作用，岩块可能绕底面发生转动，这种破坏模式称为块状倾倒破坏.块状-弯曲复合倾倒破坏是两种破坏模式的组合，指边坡中既有块状倾倒的岩块，也有发生弯曲倾倒破坏的岩块.

对于上述三种倾倒破坏模式，国内外很多学者已做了大量工作并取得了显著的成果[8-17].然而由于岩石的脆性和节理的不规则性，岩质反倾边坡还可能发生滑动-倾倒复合破坏.Alejano 等[1]通过西班牙的一个失稳矿山边坡，详细分析了边坡上部块状倾倒-下部圆弧滑动的破坏机制，并提出了相应的稳定性分析方法.Amini 和Mohtarami 等[18-19]通过室内模型试验，研究了边坡上部圆弧滑动-下部弯曲倾倒破坏的复合破坏机制，并推导了安全系数计算公式.当横向节理或裂隙并未由坡脚贯通到坡顶时，坡脚岩层由于岩块高宽比较小，可能沿横向节理发生平面滑动破坏，中部岩层可能发生块状倾倒破坏，而上部岩层由于未被横向节理切割可能发生弯曲倾倒破坏，这类破坏可称之为滑动-块状倾倒-弯曲倾倒复合破坏.

本文首先建立边坡滑动-块状倾倒-弯曲倾倒复合破坏的地质模型和力学模型，然后基于极限平衡理论和悬臂梁模型提出边坡复合破坏的稳定性分析方法，最后通过山西浑源某花岗岩矿山边坡来验证所提地质力学模型和分析方法的正确性.

1 复合倾倒破坏分析

1.1 复合倾倒破坏过程

底部横向节理未完全贯通的倾倒破坏过程如图1 所示.横向节理将岩层切割成离散的岩块，岩块区域的上部岩块由于高宽比大，在自重和层间推力作用下发生块状倾倒变形，推挤下部岩块，发生滑动-块状倾倒复合破坏；未被横向节理贯通的顶部岩层失去前缘岩块的支撑抗力之后形成悬臂段，在自重作用下发生悬臂弯曲，形成弯曲倾倒破坏；边坡完全倾倒破坏后，形成“L”型的破坏形态.

复合倾倒破坏主要为边坡前缘和中部岩块发生滑动-块状倾倒复合破坏，而后伴随后缘岩层发生弯曲倾倒破坏.因此，可将此类复合破坏分为3 个分区：滑动区、块状倾倒区和弯曲倾倒区（如图1 所示）.

图1 复合倾倒破坏示意图Fig.1 Diagram of complex toppling failure

1.2 地质几何模型

岩质反倾边坡复合倾倒破坏的分析模型如图2所示，图中h 为边坡高度，hi为岩块i 的高度，t 为岩块厚度，α 为边坡坡度，θ 为裂隙带倾角，β 为反倾结构面法线倾角，θr为裂隙带与反倾结构面法线夹角，θr=θ-β，η 为反倾结构面倾角，η=90°-β.

图2 复合倾倒破坏地质几何模型Fig.2 Geological geometric model of complex toppling failure

破坏面以上任意岩块的自重为：

式中：γ 为岩体重度；i 为自坡脚向上的四边形岩块编号，1≤i≤itotal（1 为横向节理贯通的坡脚第一个岩块，itotal为横向节理贯通的最后一个岩块）.

1.3 力学分析方程

复合倾倒破坏是一个十分复杂的过程，要想构建完全精确的力学分析方程是不太可能的，但是可以通过合理的假设和简化得到满足工程精度要求的分析方程.本文沿用了以下几条基本假设来简化复合倾倒破坏的分析过程[7-15].

1）底部横向节理起始于坡脚位置，且滑动区和块状倾倒区岩块沿横向节理发生破坏.

2）岩块发生滑动破坏时，假设岩层间无相互错动，只考虑层面法向力Pi，底滑面满足极限摩擦平衡条件Si=Nitan φ1，Si、Ni和φ1分别为滑动破坏面的切向力、法向力和摩擦角.

3）岩块发生块状倾倒破坏时，层间相互作用力简化成集中力，作用点位于岩块界面最上端，层面满足极限摩擦平衡条件Qi= Titan φ2，Qi、Ti和φ2分别为倾倒层面的切向力、法向力和摩擦角.

4）所有潜在破坏岩层具有相同的安全系数，且都等于边坡的整体安全系数Fs.

根据反倾边坡的复合倾倒过程，从坡脚向坡顶的方向逐步对岩块进行稳定性分析，首先对坡脚第1 个岩块进行力学分析，如图3 所示.

对于坡脚第1 个岩块，按照剪切滑移进行分析，沿破坏面和垂直破坏面建立平衡方程如下：

整理上式可得发生剪切滑移破坏时所需第2 个岩块作用的最小推力为：

图3 坡脚第1 个岩块力学模型Fig.3 Mechanical model of the first block located at the slope toe

对于坡脚第1 个岩块，按照块状倾倒破坏进行分析，以岩块破坏面下端点为转折点，建立力矩平衡方程如下：

整理上式可得发生块状倾倒破坏时所需第2 个岩块作用的最小推力为：

P1、T1的相对大小决定坡脚第1 个岩块的潜在破坏模式.若P1≤T1，则坡脚第1 个岩块潜在的破坏模式为剪切滑移破坏；若P1＞T1，则坡脚第1 个岩块潜在的破坏模式为块状倾倒破坏.

同理，岩块i 按照剪切滑移进行分析时，力学模型如图4（a）所示，沿破坏面和垂直破坏面建立平衡方程如下：

图4 第i 个岩块力学模型Fig.4 Mechanical model of the block i

整理上式可得发生剪切滑移破坏时所需上部岩块作用的最小推力为：

岩块i 按照块状倾倒破坏进行分析时，力学模型如图4（b）所示，以岩块破坏面下端点为转折点，建立力矩平衡方程如下：

整理上式可得发生块状倾倒破坏时所需上部岩块作用的最小推力为：

若块状倾倒区中先有部分岩块和滑动区岩块发生滑动-块状倾倒复合破坏，块状倾倒区后部存在残留岩块，岩块处于临空状态，层间作用力变为零，力学模型如图5 所示，以岩块破坏面下端点为转折点，建立力矩平衡方程如下：

整理上式可得处于临空状态的岩块发生块状倾倒破坏时所需满足的最小高宽比χmin为：

图5 块状倾倒区处于临空状态的岩块力学模型Fig.5 Mechanical model of the block toppling at the free surface

滑动区和块状倾倒区的岩块全部发生破坏后，对弯曲倾倒区形成反坡临空面，其后缘岩块处于悬臂状态.因为下部岩块破坏后与上部岩块分离，层间作用力变为零，所以弯曲倾倒区的岩块稳定性问题可转化为“斜置悬臂梁”问题，左保成[4]、卢海峰等[20]、陈从新等[21]基于图6 所示的斜置悬臂梁模型，推导了单岩层折断所需满足的最小高度hfmin为：

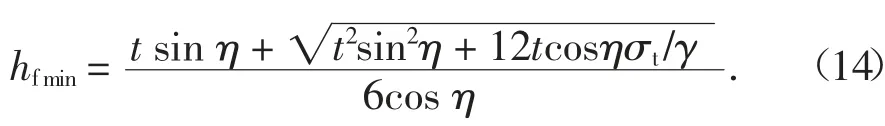
图6 弯曲倾倒力学模型[4，20-21]Fig.6 Mechanical model of the flexural toppling[4，20-21]

1.4 破坏类型和分析方法

本文所提反倾边坡滑动-块状倾倒-弯曲倾倒复合破坏，主要为边坡前缘和中部岩块先发生滑动-块状倾倒复合破坏，而后伴随后缘岩层发生弯曲倾倒破坏.从复合倾倒破坏过程来看，块状倾倒区的岩块可能全部和滑动区岩块先发生滑动-块状倾倒复合破坏，也可能只有部分和滑动区岩块先发生滑动-块状倾倒复合破坏.

1.4.1 块状倾倒区岩块全部发生复合破坏

以式（9）和（11）作为迭代方程，取Fs=1，从坡脚岩块向横向节理贯通的最后一个岩块计算，将每一步迭代得到的min（Ti-1，Pi-1）值作为下一步迭代计算中的Ti和Pi，取Fi= min（Ti，Pi）（1≤i≤itotal），即边坡失稳破坏时所需的附加外力.若横向节理贯通的最后一个岩块计算所得附加外力Fitotal＜0，则块状倾倒区的岩块全部发生破坏.滑动区和块状倾倒区的岩块发生复合破坏后，形成反坡临空面，其后缘弯曲倾倒区岩块的稳定性可通过式（14）计算分析.

此外滑动区与块状倾倒区的边界可通过式（15）获得[21].若岩块ist及ist+1 破坏时需要上部岩块作用的推力满足式（15），则[1，ist]属于潜在滑动区，（ist，itotal]属于潜在块状倾倒区.

式中：Pist和Pist+1分别为式（9）求得岩块ist及ist+1 破坏时需要上部岩块作用的推力；Tist和Tist+1分别为式（11）求得岩块ist及ist+1 破坏时需要上部岩块作用的推力.

边坡安全系数Fs主要由滑动-块状倾倒复合破坏区域的岩块稳定性决定.先假定一个初始安全系数F（0）s，以式（9）和（11）作为迭代方程，从坡脚岩块开始向该复合破坏区域的最后一个岩块计算，求出附加外力F，直到假定的Fs满足F 为零的要求.

1.4.2 块状倾倒区岩块部分发生复合破坏

以式（9）和（11）作为迭代方程，取Fs=1，从坡脚岩块向横向节理贯通的最后一个岩块计算，将每一步迭代得到的min（Ti-1，Pi-1）值作为下一步迭代计算中的Ti和Pi，取Fi= min（Ti，Pi）（1≤i≤itotal），即边坡失稳破坏时所需的附加外力.若横向节理贯通的最后一个岩块计算所得附加外力Fitotal≥0，前面存在附加外力Fitotal＜0 的岩块，则块状倾倒区的岩块只有部分发生复合破坏，滑动-块状倾倒复合破坏的区域为[1，im]，进一步由式（15）可得[1，ist]属于潜在滑动区，（ist，im]属于潜在块状倾倒区.若块状倾倒区的所有岩块计算所得附加外力Fi＞0，则岩块处于稳定状态.若岩块计算所得的附加外力Fi=0，则岩块处于临界平衡状态.

块状倾倒区中，[1，im] 区域岩块发生复合破坏形成反坡临空面，其后缘（im，itotal]区域的岩块失去层间作用力，其稳定性通过式（13）计算分析.若边坡后缘（im，itotal]区域的块状倾倒区岩块全部发生块状倾倒破坏，则需通过式（14）计算弯曲倾倒区岩块稳定性.

边坡安全系数Fs也由滑动-块状倾倒复合区域的岩块稳定性决定.通过先假定一个初始安全系数F（0）s，迭代求解坡脚岩块至该复合破坏区域的最后一个岩块，直到假定的Fs满足岩块附加外力F 为零的要求.

2 工程实例数值模拟

山西省浑源县某花岗岩矿于2017 年8 月23 日发生复合倾倒破坏.倾倒破坏主体位于1 950 m 高程平台下部5～15 m 范围内，倾倒破坏区内岩块沿裂隙带发生滑动-块状倾倒复合破坏，往正面临空方向倾倒，后缘岩块因正面临空发生弯曲倾倒变形，形成“L”形的凹腔，边坡倾倒破坏前后的概貌如图7所示.

图7 反倾边坡复合倾倒破坏Fig.7 Complex toppling failure of anti-dip slope

通过倾倒破坏区域的地质调查可知，反倾边坡中存在三组优势结构面和底部裂隙带：第一组结构面J1 产状为67°∠73°，倾向北东，节理密度约为3.63 条/m，裂隙间距的平均值为27.6 cm；与坡面形态近似垂直，解除了倾倒岩体的侧向约束（因图7 为反倾边坡复合倾倒破坏的侧视图，结构面J1 垂直于反倾边坡坡面，故未展示J1 的分布）.第二组结构面J2 产状为136°∠81°，倾向北西，节理密度约为2 条/m，裂隙间距的平均值为50 cm；结构面呈张性，延伸性较好，对倾倒破坏起主控作用.第三组结构面J3产状为172°∠25°～45°，倾向南，节理密度约为1.5条/m，裂隙间距的平均值为65 cm；延伸性较差，对边坡稳定性影响较小.反倾边坡底部发育一条裂隙带，顺坡向倾向外，倾角30°，厚0.2 m，延伸约13 m. 结合边坡地质结构，考虑陡倾结构面J2、缓倾结构面J3 和底部裂隙带，得到反倾边坡地质剖面图（如图8所示）.

图8 反倾边坡地质剖面图Fig.8 The geological profile of anti-dip slope

2.1 数值模型和材料参数

反倾边坡倾倒破坏的诱发因素是持续降雨，但是期间持续降雨的累积降雨量较小，坡体中未见明显水流，故本文不考虑裂隙水在岩体裂隙间的动静水压力[22-23]，只考虑降雨对结构面力学参数的弱化作用.因此，数值模拟主要包括天然工况和降雨工况，采用UDEC 的摩尔库仑模型，计算所采用的材料参数通过室内试验、工程类比和参数反演综合得出[24]（见表1），天然工况采用天然材料参数，降雨工况采用饱和材料参数.基于图8 所示的反倾边坡地质剖面图，建立了反倾边坡的数值模型（如图9 所示）.

表1 数值模拟所采用的材料参数Tab.1 Material parameters using in numerical simulation

图9 反倾边坡UDEC 数值模型Fig.9 UDEC numerical model of anti-dip slope

边坡模型高25 m，长35 m；坡高15 m，坡度65°；内部发育两组结构面：陡倾结构面J2 倾角81°、间距1 m，缓倾结构面J3 倾角25°、间距0.8m；底部发育一条裂隙带，倾角30°，延伸约13 m.

2.2 天然工况模拟

天然工况下数值计算收敛，总共计算229 867步，最终边坡位移矢量图和坡面位移量如图10 所示.边坡整体位移变形较小，说明该边坡在天然状态下是稳定的.从图10 中具体来看：边坡坡脚岩块位移很小，底部裂隙面闭合且无滑动；坡顶岩块在自重作用下，有水平向外的倾倒趋势，但倾倒位移量较小，坡面位移量随坡高的增加近似呈线性增长，最大位移量4.4×10-3m，位于靠近坡肩的位置，边坡整体呈稳定状态.

图10 天然工况边坡位移矢量图和坡面位移量（单位：m）Fig.10 The displacement vector diagram and slope surface displacement in natural condition（unit：m）

2.3 降雨工况模拟

雨水的弱化作用导致边坡岩体和结构面的力学参数降低，在饱和力学参数条件下，数值计算不收敛，说明该边坡在降雨状态下是失稳的.

图11 所示为降雨工况下，边坡计算50 万步时的位移矢量图和坡面位移量.

从图11 中可以看出，降雨工况下边坡整体位移变形较大，坡面位移量随坡高不再呈线性增长，而是呈现明显的分区特征，具体可分为滑动区、块状倾倒区和弯曲倾倒区，岩块最大位移7.5×10-2m，位于块状倾倒区后缘顶部的位置.根据边坡的位移矢量特征（箭头方向表示位移方向，箭头长度表示位移大小）可进一步得出三个分区的岩块位移特征：滑动区集中在坡脚位置，主要为前三个岩块，位移方向为平行于底部裂隙面向下，岩块各高度位移大小近似相等，呈整体向下剪切滑动的特征.块状倾倒区主要位于滑动区上方，位移方向近似水平向外，岩块顶部位移大，底部位移小，位移矢量近似垂直于反倾结构面，呈现沿底部裂隙面下端点向外转动倾倒的特征.弯曲倾倒区岩块底部没有贯通的裂隙带，发生弯曲倾倒变形，处于弯曲变形状态.因此复合倾倒主要破坏为块状倾倒区岩块先发生倾倒破坏，挤压推动前部岩块，触发前缘岩块发生滑动破坏.

图11 降雨工况边坡位移矢量图和坡面位移量（单位：m）Fig.11 The displacement vector diagram and slope surface displacement in rainfall condition（unit：m）

图12 所示为降雨工况下，边坡计算50 万步时的塑性区和局部破坏图.弯曲倾倒区位于块状倾倒区的上方，岩块底部后侧出现局部拉伸屈服破坏，前侧出现局部剪切破坏（图12 中小圆圈表示拉伸破坏塑性区，星号表示剪切破坏塑性区），呈现向外弯曲倾倒的特征.因弯曲倾倒区的岩块弯曲拉应力未达到其抗拉强度，故弯曲倾倒区的岩块未出现倾倒破坏，处于弯曲变形状态.因此，降雨工况下边坡先发生前缘和中部滑动-块状倾倒破坏，并伴随后缘岩块弯曲倾倒变形.

此外，从滑动区最后一个岩块失稳的局部放大图（A1）可看出滑动区岩块的破坏特征：该岩块底部与裂隙带（破坏面）压密闭合，相互剪切错动，发生压剪滑移破坏；岩块后部出现图中所示的明显张裂隙，张裂隙呈现顶部窄底部宽的形态，这主要是由于后部岩块沿底部下端点发生转动倾倒，上部变形大于下部，上部挤推前部岩块，致使滑动区后缘岩块的下部形成“张裂隙”，此张裂隙可作为滑动区和块状倾倒区的分界面.从块状倾倒区的最后一个岩块失稳的局部放大图（A2）可看出：块状倾倒区的岩块在底部和后部存在两条张裂隙，底部张裂隙沿破坏面呈现前窄后宽的形态，后部张裂隙沿岩块高度呈现顶宽底窄的形态，表现出明显的块状倾倒特征.因此，从岩块失稳的局部放大图进一步肯定了该边坡的滑动-块状倾倒复合破坏特征.

图12 降雨工况边坡塑性区和局部破坏图Fig.12 The plastic zone and local failure in rainfall condition

图11 和图12 的UDEC 模拟结果均一致反映了底部横向节理未贯通的反倾边坡的复合破坏机制，表现为前缘和中部滑动-块状倾倒破坏，而后伴随后缘岩块弯曲倾倒变形.

为便于理论公式的计算分析，提出了反倾边坡简化地质模型，即不考虑缓倾结构面J3 的影响.对该简化地质模型采用相同的饱和材料参数，计算50万步可得降雨工况下边坡位移矢量和局部破坏如图13 所示.

从图13 中简化地质模型边坡的位移矢量来看，依然呈现滑动区、块状倾倒区和弯曲倾倒区三个分区特征，滑动区和块状倾倒区的位移矢量特征和原始地质模型完全一致，弯曲倾倒区由于不考虑缓倾结构面J3，岩块的变形比原始地质模型稍微偏小.总体来看，简化地质模型的边坡位移矢量特征和塑性区分布也表现出滑动-块状倾倒-弯曲倾倒复合破坏机制，这和图11 与图12 原始边坡地质模型所得结果一致.此外，对比分析滑动区岩块的局部失稳图A1′和A1，后部张裂隙形状均呈现压剪滑移破坏特征；块状倾倒区的局部失稳图A2′和A2，底部和后部两条张裂隙形状均一致呈现出块状倾倒特征.因此从边坡位移矢量和局部破坏特征可知该反倾边坡中的缓倾结构面J3 对边坡的破坏无显著影响，采用简化地质模型研究边坡破坏机制和分析方法是合理的.

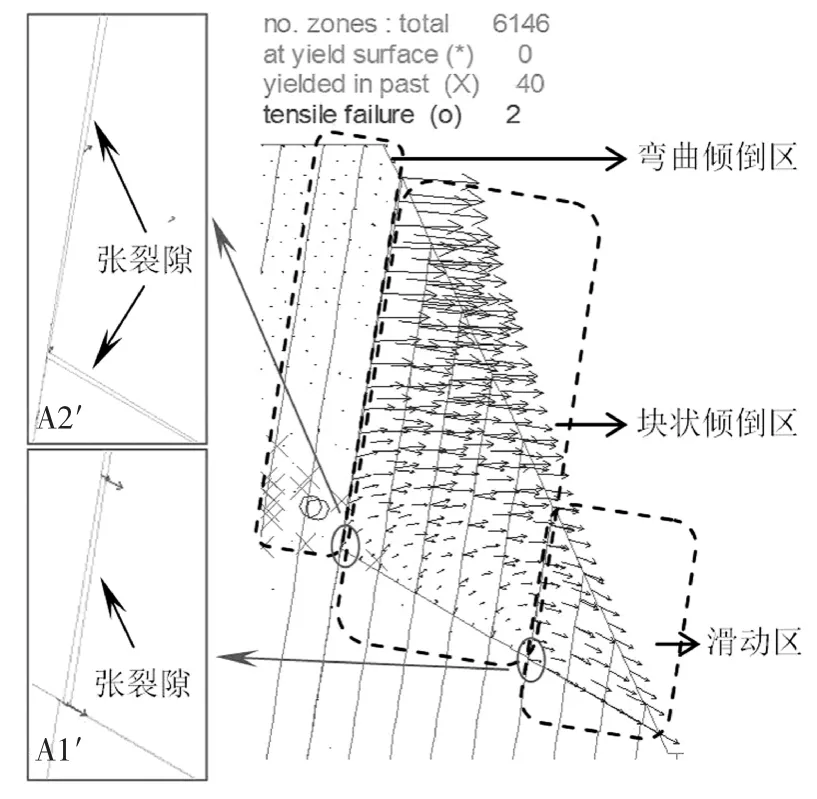
图13 降雨工况下简化边坡模型数值模拟结果Fig.13 Numerical simulation result of simplified model in rainfall condition

3 对比分析

文中实例边坡的复合倾倒破坏机制，通过数值模拟具体表现为边坡前缘和中部岩块发生滑动-块状倾倒破坏，后缘岩块发生弯曲倾倒变形.在表1 所示的材料参数条件下采用本文所提复合倾倒破坏分析方法对该反倾边坡简化地质模型进行计算分析，计算模型如图14 所示.

图14 复合倾倒破坏简化计算模型Fig.14 Simplified calculation model of complex toppling failure

按照1.4 节的分析步骤，首先取Fs=1，以式（9）和（11）作为迭代方程，从坡脚岩块（i=1）向横向节理贯通的最后一个岩块（i=8）计算，将每一步迭代得到的min（Ti-1，Pi-1）值作为下一步迭代计算中的Ti和Pi，取Fi= min（Ti，Pi）（1≤i≤8），即边坡失稳破坏时所需的附加外力.在饱和材料参数条件下，滑动-块状倾倒破坏区域的各岩块发生滑动破坏或块状倾倒破坏所需附加外力Pi和Ti，见表2.从表2 中各岩块滑动破坏或块状倾倒破坏时所需附加外力来看，依据较小附加外力所对应的类型即为岩块的潜在破坏类型，可清楚地判定各岩块的破坏类型，如表2 所示.此外，第8 号坡顶岩块所需附加外力小于零，处于失稳状态，顶部岩块倾倒加压于下部块体是导致边坡发生滑动-块状倾倒复合破坏的根本原因，故对该类边坡治理加固时应及早采取措施，重点加固块状倾倒破坏区.

表2 理论计算结果Tab.2 The results by theoretical calculation methods

进一步对理论方法和数值模拟的计算结果作对比分析，如表3 所示.从表3 中可看出，利用本文所提的理论方法和数值模拟得到的结果近似一致，两种方法计算的边坡稳定性结果均处于失稳状态，两种方法确定的滑动区和块状倾倒区的范围基本相同，均与实际相符.此外，对于弯曲倾倒区的岩块，通过式（14）计算得岩块最小折断高度为24 m，远大于该边坡弯曲倾倒区的岩块悬臂长度10 m，因此岩块仅处于弯曲变形状态，并未发生弯曲倾倒破坏，这也与数值模拟的结果一致.

表3 两种计算方法结果对比Tab.3 Comparison of the results by two kinds of different calculation methods

边坡安全系数Fs以式（9）和（11）作为迭代方程，从坡脚岩块开始向该复合破坏区域的最后一个岩块计算，求出附加外力F，直到假定的Fs满足F 为零的要求.对该实例边坡采用天然材料参数计算得安全系数Fs为1.35，Fs＞1 说明边坡处于稳定状态；采用饱和材料参数计算得安全系数Fs为0.96，Fs＜1 说明边坡处于失稳状态.从边坡安全系数角度考虑，理论方法和数值模拟的结果亦一致.

4 结 论

1）基于底部横向裂隙未完全贯通的反倾边坡，建立了包含滑动区、块状倾倒区和弯曲倾倒区的复合倾倒破坏地质模型.

2）利用三个分区的岩块破坏特点，基于极限平衡理论和悬臂梁模型，提出了岩质反倾边坡复合倾倒破坏自下而上逐步分析的理论方法.

3）岩质反倾边坡滑动-块状倾倒-弯曲倾倒复合破坏的稳定性由滑动-块状倾倒复合破坏区域控制.

4）滑动-块状倾倒复合破坏区中块状倾倒区域属于主动破坏区域，滑动区属于被动破坏区域，治理加固时应重点加固块状倾倒破坏区.