雷暴冲击风作用下高层建筑风荷载频域特性

方智远，汪之松，2†，李正良，2

（1. 重庆大学 土木工程学院，重庆400045；2.山地城镇建设与新技术教育部重点实验室（重庆大学），重庆400045）

风荷载是高层建筑结构设计的主要控制荷载，以往对于风荷载的研究主要集中在边界层风场.随着风工程研究的逐步深入，越来越多的学者开始将目光转向台风、龙卷风以及雷暴冲击风等的研究.雷暴冲击风是雷暴天气中下沉气流冲击地面形成的一种灾害性强风，是许多非台风地区极值风速出现的主要原因，在世界各地造成了大量工程结构破坏[1].开展雷暴冲击风作用下高层建筑风荷载频域特性研究对于进一步认识雷暴风的作用机理以及完善高层建筑的抗风设计具有重要意义.

在大气边界层风场中，国内外学者已开展了大量针对高层建筑风荷载频域特性的研究.Lin 等[2]研究了矩形高层建筑表面风压的幅值和频谱特性，并对整体气动力进行了研究；顾明等[3]在边界层风洞中对10 个典型超高层建筑模型进行了测压试验，分析了模型层风荷载的频域特征；曾加东等[4-5]通过刚性模型测压试验研究了矩形断面高层建筑表面风压及风荷载的频谱特性及空间相关性.

对于雷暴冲击风，Jesson 等[6]根据冲击射流试验研究了常见建筑的气动力特性；Zhang 等[7]通过试验研究了不同径向位置处的高层建筑表面平均和脉动风压分布特征；汪之松等[8-9]采用试验和数值模拟相结合的方法，对比了下击暴流作用下平地和坡地高层建筑的风荷载特性，研究了坡地坡度对高层建筑表面风压的影响；方智远等[10]采用冲击射流装置研究了雷暴冲击风作用下不同深宽比的高层建筑风压幅值特性，并与大气边界层风作用下的风压幅值进行了对比；邹鑫等[11]通过试验研究了稳态冲击风作用下的高层建筑风荷载的幅值和频谱特征.上述研究虽然给出了雷暴冲击风作用下高层建筑风荷载的一些特征，但针对该极端风场下高层建筑局部风荷载频域特性的研究仍相对较少.

本文采用冲击射流装置模拟雷暴冲击风，分别对5 种不同深宽比（D/B）的高层建筑模型在8 个典型径向位置处进行了同步测压试验，详细研究了层风荷载功率谱、相关系数以及相干函数等频域特征.研究结果有利于深入认识雷暴冲击风作用下高层建筑风荷载特性，并为建立雷暴冲击风作用下高层建筑风振计算的数学模型提供一定的研究基础.

1 试验概况

1.1 冲击射流装置

试验采用浙江大学的冲击射流装置进行，该装置主要由射流喷桶、平板以及测量系统组成.如图1所示，喷口直径Djet=0.6 m，喷口到平板的距离Hjet=1.2 m，射流速度Vjet=12 m/s.

图1 冲击射流装置Fig.1 Impinging jet experimental device

1.2 测压模型及试验工况

选取5 种不同深宽比（D/B）的矩形断面高层建筑刚性模型进行试验研究，模型几何缩尺比为1 ∶1 000，模型具体参数如表1 所示.图2 给出了测点布置及测点层划分情况，模型沿高度布置8 个测点层，测点高度从下到上依次为5 mm、15 mm、25 mm、40 mm、60 mm、75 mm、85 mm 和95 mm，后文对应采用0.05H、0.15H、0.25H、0.4H、0.6H、0.75H、0.85H、0.95H对各测点层高度进行表示. 模型1（M1）至模型4（M4）各层测点数均为12 个，即各面均匀布置3 个测点.模型5 各层测点数为14 个，其中迎风面和背风面各布置3 个测点，两侧面各均匀布置4 个测点.

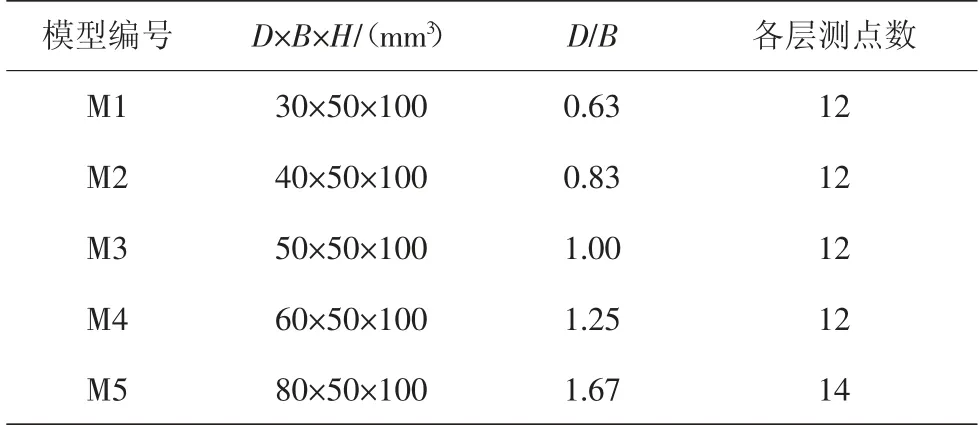
表1 不同深宽比建筑模型参数Tab.1 Parameters of different aspect ratio building model

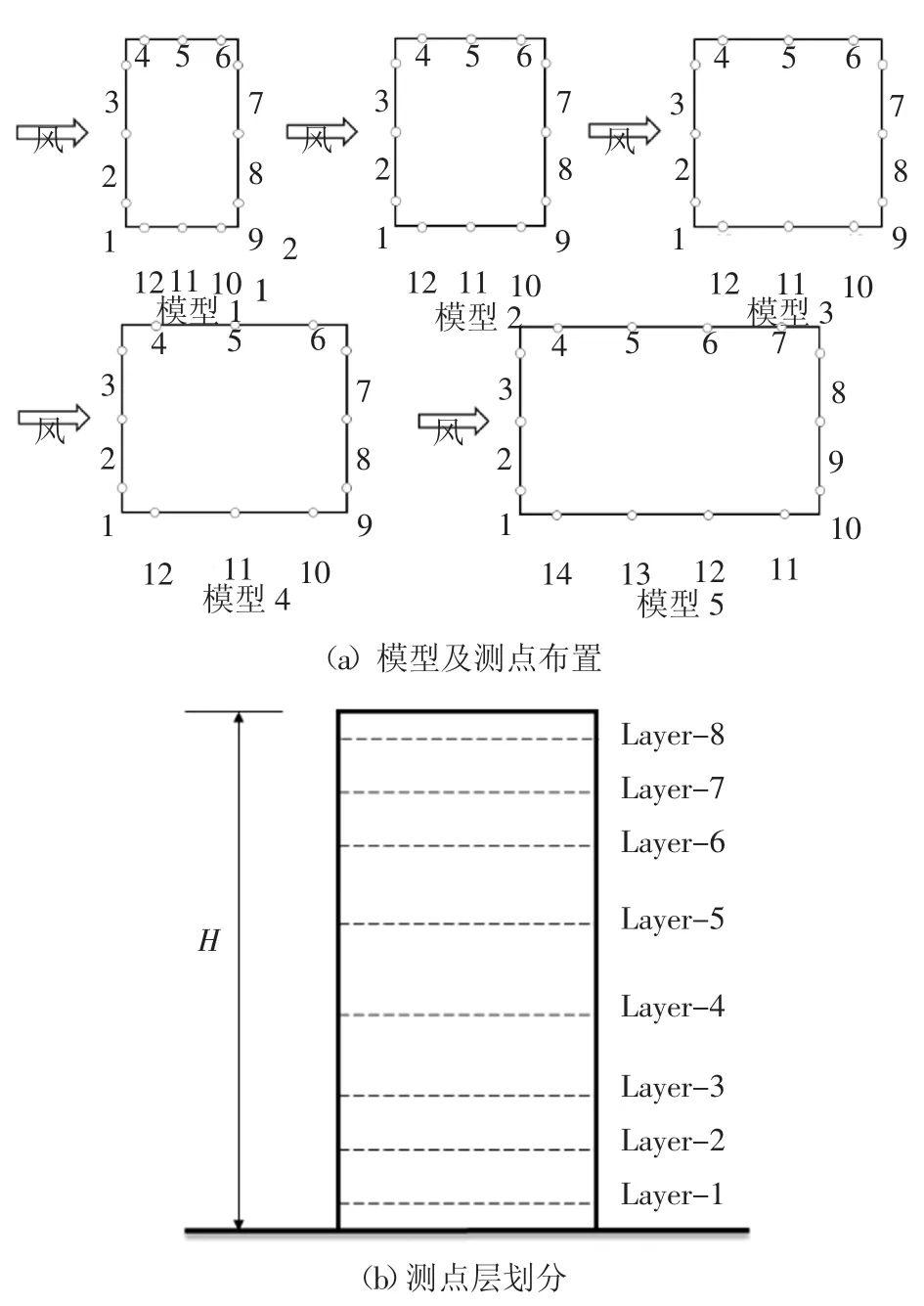
图2 模型及测点层布置Fig.2 Model and measurement layers

试验分别测试了上述5 种不同深宽比（D/B）的高层建筑模型位于r=1Djet、r=1.25Djet、r=1.5Djet、r=1.75Djet、r=2Djet、r=2.25Djet、r=2.5Djet、r=3Djet径向位置处的测点风压，如图3 所示，r 为建筑模型到射流喷口中心线的水平距离，测点的采样频率为312.5 Hz，采样时间为32 s.图4 给出了建筑模型与来流风的相对位置关系，即以宽度（B）所在表面作为模型的迎风面，顺风向的气动力为阻力，横风向的气动力为升力，扭转向的气动力为扭矩.

图3 建筑测压试验布置Fig.3 Arrangement of building pressure test

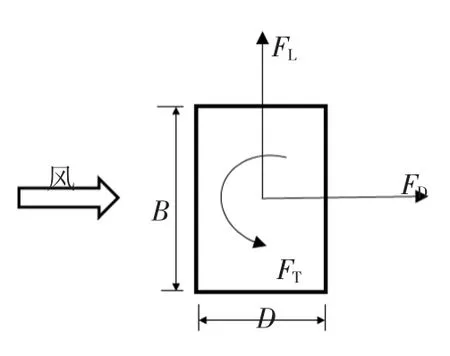
图4 气动力示意图Fig.4 Schematic of aerodynamic force

1.3 风场基本特征

图5 和图6 分别给出了采用热线探头测得的风场中不同径向位置处水平风速和湍流度的竖直剖面.从图中可看出，风场中水平风速和湍流度沿径向距离变化显著，且与常规大气边界层风场存在较大差别.图7 给出了试验风剖面与已有的实测数据[12]、试验结果[13]及经验风剖面模型[14]的对比结果，从图中可看出，试验结果与已有实测数据等取得了较好的一致性，验证了试验结果的有效性.图8 给出了z=25 mm（对应模型第3 层测点高度）高度处5 个典型径向位置的顺风向脉动风速功率谱，由图可知，不同径向位置处的风速谱存在显著差别.

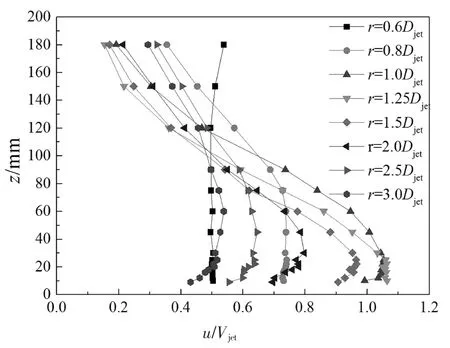
图5 水平风速竖直风剖面Fig.5 Vertical profiles of horizontal velocity

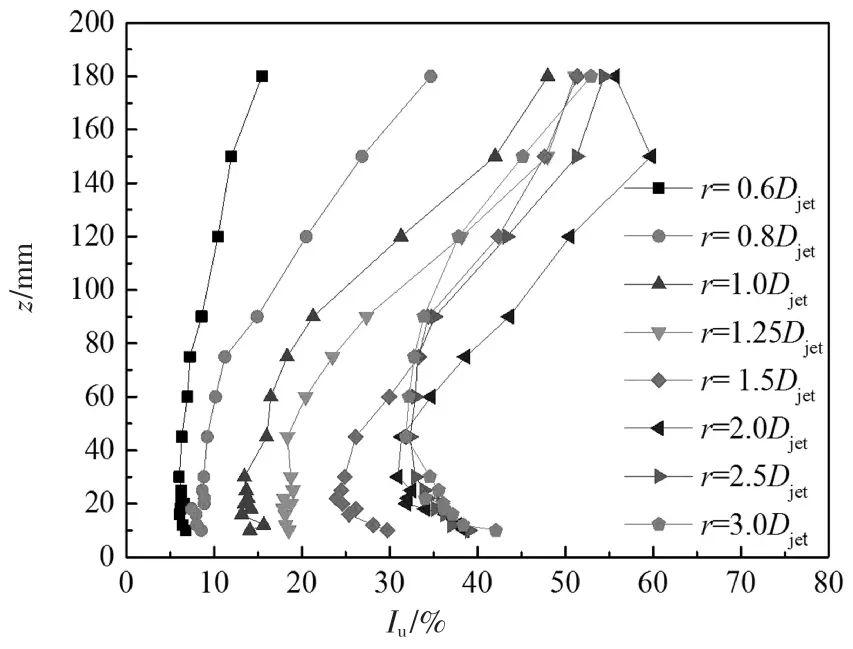
图6 湍流度剖面Fig.6 Turbulence intensity profiles

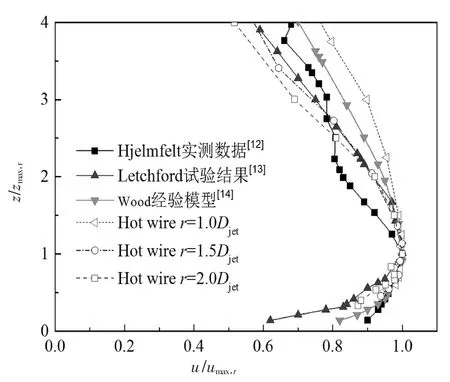
图7 竖直风剖面对比Fig.7 Comparison of vertical wind profiles

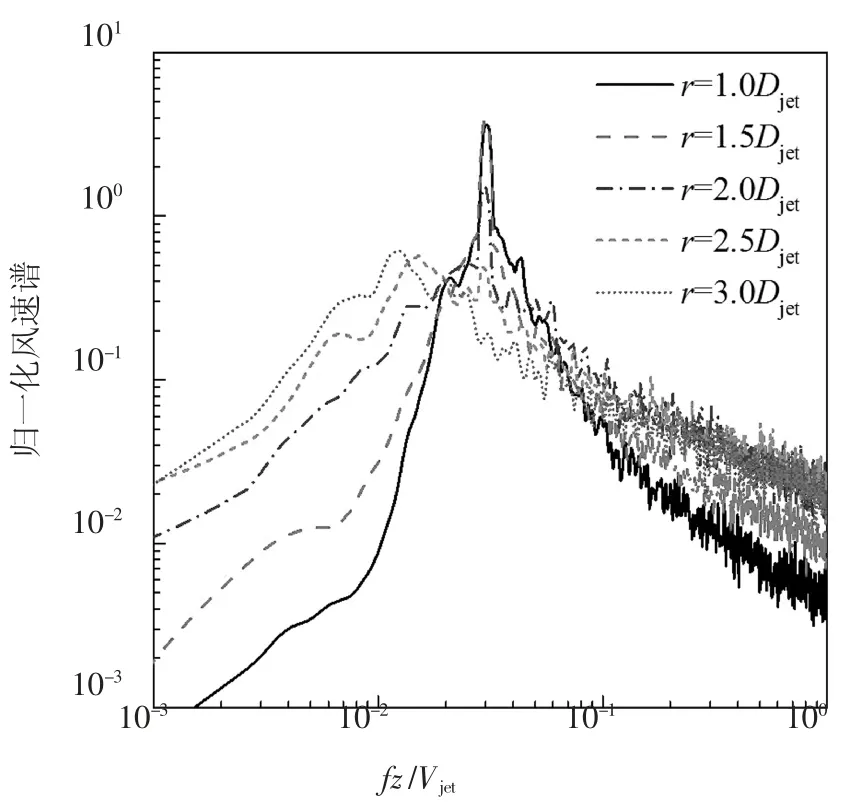
图8 脉动风功率谱Fig.8 Power spectrum density of fluctuating wind velocity

2 数据处理

为了研究下击暴流作用下不同深宽比的矩形断面高层建筑局部风荷载特性，通过对各层测点风压结果的积分处理，得到了模型各层的阻力系数CD、升力系数CL以及扭矩系数CT的平均值和均方根，各系数定义如下：

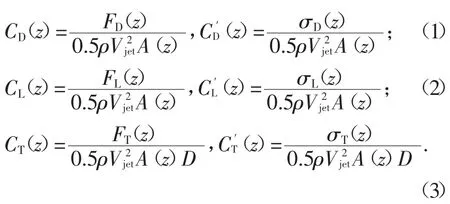
式中：CD（z）和C′D（z）为模型z 高度顺风向层阻力系数的平均值和均方根值；FD（z）和σD（z）分别为模型z高度顺风向层平均风力和脉动风力；CL（z）和C′L（z）为模型z 高度横风向层升力系数的平均值和均方根值；FL（z）和σL（z）分别为模型z 高度横风向层平均风力和脉动风力；CT（z）和C′T（z）为模型z 高度层扭矩系数的平均值和均方根值；FT（z）和σT（z）分别为模型z 高度层扭矩的平均值和脉动值；z 为测点层所在高度；A（z）为z 高度测点层的迎风面面积；ρ 为空气密度；Vjet为喷口的射流速度.

3 风荷载功率谱

通过数据处理得到了5 种不同深宽比（D/B）高层建筑模型在各典型径向位置处的层风荷载功率谱.首先给出了方形建筑在r=1.0Djet径向位置处各层的三分力系数功率谱，而后以第3 层为例，分别研究模型所在径向位置及深宽比（D/B）对层风荷载谱的影响.

3.1 层风荷载功率谱

图9 给出了方形建筑在r=1.0Djet径向位置处各层的三分力系数功率谱，从图中可看出：

1）各层阻力系数谱的主导频率基本相同，均在折减频率0.06 左右存在峰值，且模型中下部区域峰值最大，峰值频率带宽在三、四层左右最窄，随着楼层高度的增加，频带逐渐变宽，功率谱峰值逐渐减小.表明层阻力在模型中下部能量较强且较为集中，而在上部楼层范围内，则随着高度的增加，能量逐渐减弱且较为分散.

2）各层升力系数谱的主导折减频率在0.1 左右.在低频段，模型中下部楼层谱值较大，而在高频段，模型上部楼层谱值较大.

3）扭矩主要是由模型侧面不对称的升力作用以及背风面压力脉动引起的，由于旋涡脱落以及流体分离再附等都会对扭矩产生影响，故不同高度的层扭矩系数谱差异较大.模型1～5 层的扭矩系数谱的峰值频带较宽且峰值较小，而6～8 层峰值频率较为集中且峰值较大，模型中下部区域层扭矩系数谱谱值在高频段明显大于上部楼层.

3.2 D/B 的影响

图10 给出了不同深宽比（D/B）的模型位于r=1.0Djet径向位置时的三分力系数谱.从图中可看出：

1）各模型的顺风向阻力系数谱在折减频率0.06附近存在显著尖峰，且D/B=1.0 时峰值最小，说明方形建筑的层阻力在主导频率下能量相对较小.

2）在常规大气边界层风场中，矩形高层建筑的升力及扭矩系数谱主要受漩涡脱落的影响，且谱峰对应的折算频率（斯托罗哈数）随模型截面尺寸的变化应有所不同.然而从图10（b）和（c）中可看出，在雷暴冲击风作用下，上述规律并不明显，这可能是由于雷暴风在近地面与常规大气边界层风在湍流度、频谱分布上存在显著差异，从而导致了其风荷载作用机理的不同.

图9 层风力系数谱（D/B=1.0，r=1.0Djet）Fig.9 Spectra of fluctuating wind force on each layers（D/B=1.0，r=1.0Djet）

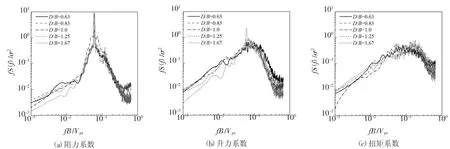
图10 层风力系数谱（第三层，r=1.0Djet）Fig.10 Spectra of fluctuating wind force on each layers（layer3，r=1.0Djet）

3.3 径向位置的影响

图11 给出了方形建筑模型处于5 个典型径向位置时的三分力系数谱.从图中可看出：

1）顺风向阻力系数谱主要受来流脉动风的影响，其峰值频率与风速谱主频基本一致，随着径向距离的增加，模型阻力系数谱的频带变宽，主频及能量逐渐减小.

2）随着径向距离的增加，升力系数谱的主导频率略有减小，但整体分布规律较为一致.

3）扭矩系数谱的主导频率随径向距离的增加略有减小.在低频段，谱值基本随径向距离的增大而增大.在高频段，谱值基本随径向距离的增大而减小.

4 脉动三分力系数的相关系数

脉动三分力系数的相关系数能够表征层风荷载在空间上的相关性，其表达式定义如下：

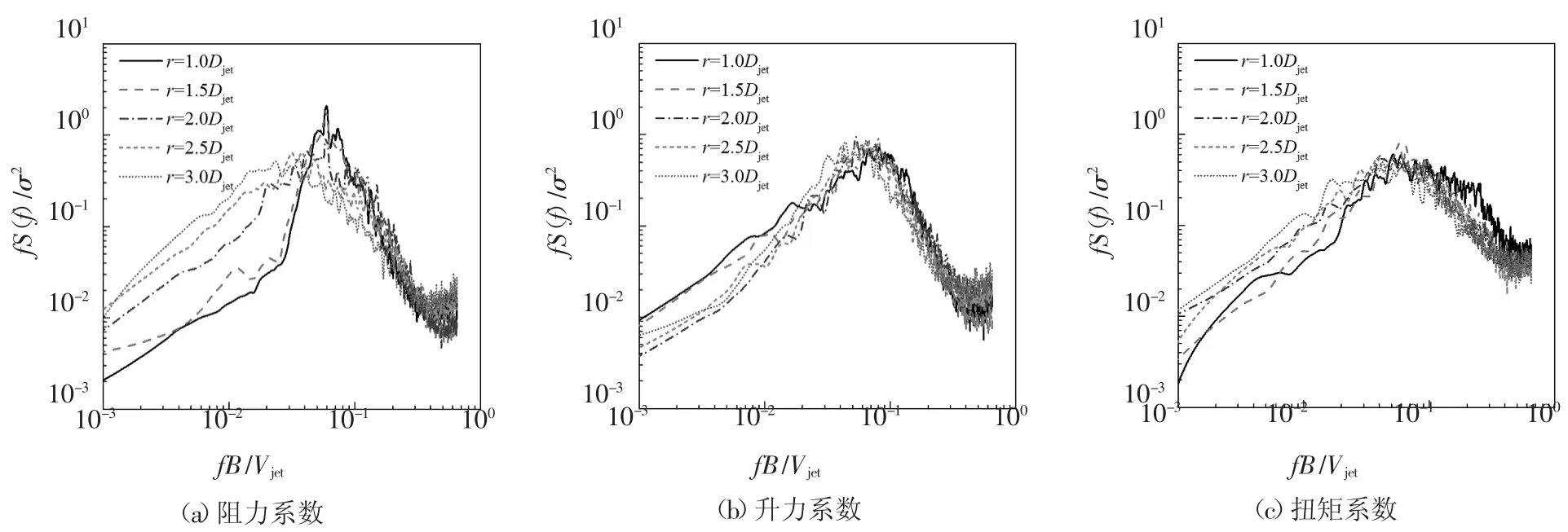
图11 层风力系数谱（第三层，D/B=1.0）Fig.11 Spectra of fluctuating wind force on each layers（layer3，D/B=1.0）

式中：σij为第i层与第j层层风荷载的协方差；σi和σj分别是第i层与第j层层风荷载的均方根.限于篇幅，本文均以顶层三分力系数为基准，分析模型各层与顶层三分力系数间的相关性，图12 与图13 横坐标中的Δz表示各层与顶层的高差，H表示模型高度.

图12 层风荷载相关系数（D/B=1.0）Fig.12 Cross-correlation coefficients of wind load on layers（D/B=1.0）

图12 以方形建筑为例，给出了各层三分力系数的相关系数在8 个典型径向位置处的分布特征.从图中可看出：

1）层阻力系数的相关性随层间距离的增大整体呈指数形式减小，但模型底部楼层与顶层的相关性则略有上升.随着径向距离的增大，层阻力系数的相关性先增大后减小，在r=2.0Djet附近相关性最小.

2）层升力系数的相关性随层间距离的增大整体呈指数形式减小，但减小幅度相对较小.层升力系数的相关性在r=1.0Djet和r=1.25Djet时较大，而在其余径向位置则相对较小且数值较为接近.

3）当r≤1.5Djet时，层扭矩系数的相关性随层间距离的增大呈波动变化，z=0.7（即模型第3 层）时相关系数最小.当r>1.5Djet时，层扭矩系数的相关性整体随层间距离的增大呈指数形式减小，且随径向距离的增大而增大.

图13 给出了各模型在r=1.0Djet位置时各层三分力系数的相关系数.从图中可看出：

1）当D/B≤1 时，层阻力系数相关性整体随D/B的增大而减小，而当D/B>1 时，相关性随D/B的增大而增大，D/B=1 时，层阻力系数的相关性最小.

2）当Δz<0.5（即模型上部楼层）时，层升力系数的相关性随D/B的增大变化较为不规则. 而当z≥0.5（即模型中下部楼层）时，对于D/B≥1.0 的模型，层升力系数相关性较大且数值较为接近，对于D/B<1.0 的模型，相关性随D/B的增大而增大.

3）各模型层扭矩系数的相关性整体随D/B的增大而减小，但当模型截面为方形（D/B=1.0）或较为接近方形（D/B=0.83）时，相关性随层间距离的增大呈不规则变化，这可能是由于方形建筑处于模型截面由宽扁形向细长形变化的临界状态，气流在模型侧面的分离再附以及尾流在模型背风面的压力脉动等在该截面下都会产生较为显著的变化，进而导致层扭矩系数相关性沿高度变化的不规则.

5 脉动三分力系数的相干性

为研究层风荷载在频域上的相关性，以方形建筑为例，根据各楼层与模型顶层的空间位置关系，分别给出了其与第7 层、第5 层以及第3 层的相干函数及相位角.

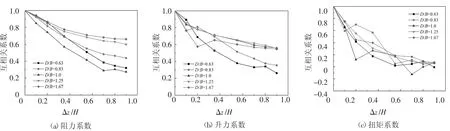
图13 层风荷载相关系数（r=1.0Djet）Fig.13 Cross-correlation coefficients of wind load on layers（r=1.0Djet）

图14 给出了各典型楼层关于第8 层脉动三分力系数的相干函数.从图中可看出：层阻力系数的相干函数在折减频率为0 时相干性最大，随着频率的增大，相干函数基本呈线性减小.相干性基本随楼层间竖向距离的增大而减小；层升力系数在折减频率小于0.1 时存在较强的相干性，而后随着频率的增大，相干函数整体呈指数衰减.层扭矩系数的相干性相对较小，相干函数随频率的增大整体按指数率迅速衰减.

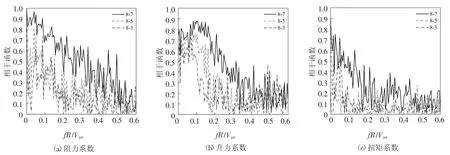
图14 典型楼层层风力系数相干函数（D/B=1.0，r=1.0Djet）Fig.14 Coherence function of wind force coefficients between typical layers（D/B=1.0，r=1.0Djet）

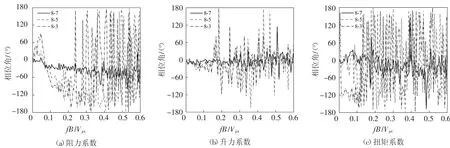
图15 典型楼层间层风力系数相位角（D/B=1.0，r=1.0Djet）Fig.15 Phase angle of wind force coefficients between typical layers（D/B=1.0，r=1.0Djet）

图15 给出了与图14 对应的相位角变化曲线.从图中可看出，三分力系数的相位角均在折减频率0.1 以内保持相对平稳变化，说明在该折减频率范围内三分力系数在临近楼层间基本保持同步脉动，而在竖向距离较大的楼层间则按一定的相位差进行有规律的脉动变化.除相邻楼层（8-7）外，层间三分力系数的相位角在高频范围内均产生大幅波动，层扭矩系数相位角的波动尤为剧烈，说明在高频段，距离较远的楼层间风荷载的同步性较差，风荷载波动明显.

6 结 论

采用冲击射流装置模拟雷暴冲击风，对5 个不同深宽比的高层建筑进行了不同径向位置处的测压试验，分析了层风荷载的频谱特征、相关系数以及相干性.结果表明：

1）各模型的顺风向阻力系数谱在折减频率0.06附近存在峰值，方形建筑的峰值相对较小.阻力系数谱主要受来流脉动风的影响，其峰值频率与风速谱主频基本一致，随着径向距离的增加，模型阻力系数谱的频带变宽，主频及能量逐渐减小.

2）不同深宽比建筑的升力和扭矩系数谱未见显著差异，考虑主要是由于雷暴风在近地面与常规大气边界层风在湍流度、频谱分布上存在显著差异，从而导致了其风荷载作用机理的不同，后续可通过数值模拟或流显技术等予以进一步研究.

3）层阻力系数的相关性随着径向距离的增大而先增大后减小.层升力系数的相关性在r=1.0Djet和r=1.25Djet时较大.当D/B≤1 时，层阻力系数相关性整体随D/B 的增大而减小；当D/B ＞1 时，相关性随D/B 的增大而增大；D/B=1 时，层阻力系数的相关性最小.

4）层阻力系数相干性随频率的增大呈线性减小.层升力系数相干性在低频段保持平稳，而后呈指数衰减，层扭矩系数相对较小，且随频率的增大而按指数率迅速衰减.