基于离散元法的反倾边坡动力破坏模式及分区研究
谌永刚,汤 华,秦雨樵
(1.安徽理工大学 土木建筑学院,安徽 淮南 232001; 2.中国科学院 武汉岩土力学研究所,湖北 武汉 430071)
在修建高速公路的过程中,因开挖而产生大量的路堑边坡。边坡的稳定性是决定路堑安全施工及运营的关键因素。反倾边坡作为一种常见的边坡类型,其岩层走向与坡面走向近一致,而岩层倾向与边坡倾向相反,稳定性相对较好,所施加的防护措施也较弱。但在高烈度区,一旦受到地震以及降雨等强扰动的作用,反倾边坡将发生大面积松动、滑塌,严重威胁高速公路的运行安全。例如2008年汶川大地震造成了约六万起落石与滑坡[1],其中四川省聚水镇因地震和降雨引发的罐滩滑坡[2],总滑移量约为4 689 104 m3,给人民的生命财产造成了巨大损失。因此对地震作用下反倾边坡的动力破坏模式的研究是十分必要的。
目前,地震作用下反倾边坡的稳定性研究主要采用3种方法,包括力学平衡分析、模型试验及数值模拟研究。力学平衡分析方面,Goodman等[3]运用极限平衡原理,得到了反倾边坡岩块处在稳定、滑动、倾倒状态的定量判别关系,并将岩块组分为滑动区、倾倒区以及稳定区。基于极限平衡原理(G-B法),将地震力简化为作用在岩块质心处的静力荷载,刘才华等[4]、G.Yagoda-Biran等[5]、郑允等[6]、Guo等[7]进一步发展了地震作用下岩块倾倒破坏的分析方法,而Miguel A.Jaimes[8]基于数值分析法研究了地震作用下刚性电气设备的抗倾覆性,认为刚性块的长宽比与抗倾覆性最相关。此外,振动台试验以及离散元数值模拟也经常应用于地震作用下反倾边坡失稳破坏的研究中[9-13]。为研究地震作用下反倾边坡动力响应规律,Li等[10]利用振动台试验及UDEC数值模拟研究了地震波特性及坡体自身结构对含节理的岩质反倾边坡稳定性的影响。Chen等[11]通过建立反倾边坡模型探究了反倾边坡在不同岩层倾角、岩基倾角、地震波频率等情况下的动力响应规律,认为地震作用下坡体顶部岩块(长细比最大)对坡体稳定性影响最大。综上所述,力学平衡解析从一定程度上构建了反倾边坡在倾倒过程中的位移模式,但无法反映倾倒变形体破坏时的运动特征以及随时间变化的运动过程,且岩块所处状态大多是通过倾倒力与抗滑力进行判断,从位移及转角方面进行判断研究较少。而模型试验虽然能够直观地反映出反倾边坡破坏过程中位移和应力的变化,但易受到模型相似比的影响,且制作周期长,成本高,研究主要集中于地震作用下反倾边坡动力响应规律及破坏模式,对反倾边坡中岩块分区以及分区特征的研究较少。
为了进一步研究反倾边坡的动力响应特征,克服上述解析法与模型试验法的缺陷,采用了UDEC离散元软件模拟了Scavia反倾边坡模型[14]在双向地震作用下的位移过程,并根据块体运动模式进行了分区研究。研究结果对今后地震作用下反倾边坡失稳产生的地质灾害的预防及采取的加固措施具有一定指导意义,同时,用位移量及转角对岩块状态做定量判断,弥补了以往力学平衡解析法的不足。
1 基于离散元方法的反倾边坡动力响应
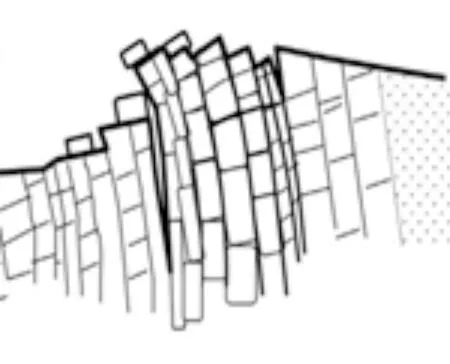
反倾边坡主要的失稳破坏模式为倾倒破坏,典型的倾倒类型有块体倾倒、弯曲倾倒、块体-弯曲倾倒(见图1)。

(a)块体倾倒

(b)弯曲倾倒
(c)块体-弯曲倾倒
倾倒主要发生在由宽距节理分割的独立岩柱上,底部短小岩块受到上部长岩块的推力而滑出,进一步诱使上部岩块发生倾倒。块体倾倒具有比较明显的破坏面,主要由阶梯状交错节理构成,通常发生在厚层沉积岩当中,例如石灰岩、砂岩及柱状节理火成岩。
在高烈度区,强震、强降雨等可能会导致反倾边坡的松动和滑塌,诱发严重的地质灾害。因此,对强震、强降雨作用下反倾边坡破坏模式的研究是十分必要的。图2为苗尾水电站潜在倾倒坡体及雅砻江上游潜在倾倒坡体,均显示出明显的块体倾倒模式。

(a)苗尾水电站潜在倾倒坡体[16]

(b)雅砻江上游潜在倾倒坡体[1]
1.1 离散元方法
离散元法是分析离散介质变形和运动趋势的有效工具,适用于求解非连续介质大变形问题,能够直观地反映岩体运动变化的应力场、位移场、速度场等各力学参量的变化[17],被广泛应用于节理化岩体、碎裂结构岩质边坡的变形破坏分析当中[18]。
1.2 模型建立
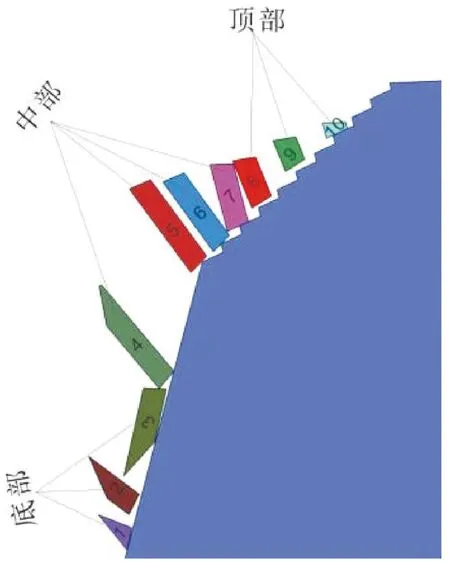
考虑到反倾边坡块体结构的离散性与非连续性,运用二维离散元UDEC软件,通过数值模拟的手段建立反倾边坡块体倾倒结构的概化模型,以研究在地震作用下岩块破坏模式及分区特征。反倾边坡理想二维离散元岩质边坡模型如图3、图4所示。考虑真实岩块的一般几何形状,初始模型采用Scavia[14]所提出的理想模型(见表1、图4),其中黄色圆圈为底边两角点,红色部分为坡体下部,蓝色部分为坡体中部,橘色部分为坡体上部,岩块自下至上部依次编号为1~10。岩体本构模型采用Mohr-Coulomb模型,节理面本构模型采用面接触-库伦滑移模型。

图3 反倾边坡模型及边界条件

图4 坡体上部岩块监测点及分区

表1 坡体结构参数
在地震作用方面,采用汶川地震主震断裂(映秀—北川断裂)附近的清平强震动台所记录的汶川波作为动力荷载,其垂直(UD)向和水平(NS)向的地震加速度曲线如图5所示。同时,选择应力方式输入地震荷载,并施加于模型底部。模型底部采用黏滞边界,两侧采用自由边界(见图3),并将地震加速度导入Seismosignal软件进行基线校正及滤波处理。
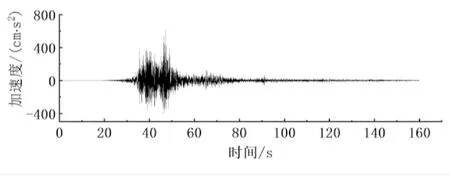
(a)UD向地震加速度曲线

(b)NS向地震加速度曲线
输入地震波的频率含量和系统的波速特性会影响波传播数值的精度。Kuhlemeyer等[19]研究表明,模型网格尺寸的大小必须小于输入波形最高频对应波长约1/10时,才能更精确地传播波的数值,即
(1)
(2)
式中:Δl为所生成三角形有限差分网格最大边长;λ为与包含可观能量的最高频率成分相关的波长;C为波的传播速度,通常取Cs与Cp中的较小者。当没有现场实测数据时,波的传播速度
(3)
(4)
式中:K为岩体体积模量;G为岩体的剪切模量;ρ为岩体质量密度。
在UDEC中,对于已经给定的网格尺寸,不导致波形失真的输入波的最高频率为
(5)
1.3 岩体、结构面物理力学参数
根据实际工程经验及数值模拟相关文献[20-22]可知,块体倾倒属于浅层倾倒,通常发生在由层状的硬性岩层构成的斜坡中,如花岗岩等[23],基于此本文采用岩体力学参数如表2、表3所示。
将表2、表3数据代入式(3)、式(4)中计算可得,Cp=4 127.6 m/s,Cs=2 185.8 m/s,则波的传播速度为C=2 185.8 m/s。波的最高频率fmax=25 Hz,由式(5)计算出波长λ=87.4 m。根据式(1)可得Δl≤8.74 m,为保证计算精度,选择网格尺寸Δl=2 m,共划分3 717个单元,产生2 021个网格节点。

表2 岩体物理力学参数

表3 结构面力学参数
2 反倾边坡动力破坏模式判别及分区
2.1 岩块破坏模式判别依据
本文选择每个岩块底边两角点作为位移监测点,读取岩块两角点运动0.1 s的坐标,计算每0.1 s块体在x,y向的位移,进一步计算每0.1 s块体底边转角。最终,利用计算得到转角与位移,结合位移转角图及统计的坐标判断岩块的破坏模式。岩块状态变化示意图如图6所示,图中红色为原始状态,黄色为运动后状态。

(a)滑动

(b)倾倒

(c)滑动-倾倒
各岩块转角、位移曲线如图7所示,右图为第34秒至第37秒的部分。由图7可以看出,当位移与转角曲线较为平稳时,即岩块底边和缓倾裂隙面与水平面夹角几乎相等且几乎不发生位移时,则说明岩块处于稳定状态;当岩块转角的曲线较为平稳而位移曲线上升时,即岩块底边与水平面夹角等于缓倾裂隙面与水平面夹角且每秒位移量差值为正值时,岩块处于滑动状态;当岩块转角曲线上升而位移曲线下降时,即岩块底边与水平面夹角大于缓倾裂隙面与水平面夹角,而每秒位移量差值为负值时,岩块处于倾倒状态;当岩块位移与转角的曲线同时上升时,即岩块底边与水平面夹角大于缓倾裂隙面与水平面夹角,且每秒位移量差值为正值时,岩块处于滑动-倾倒状态;当岩块位移曲线上升而转角的曲线下降时,岩块处在滑动-倾倒再到滑动状态。

(a)岩块1~3转角及位移曲线

(b)岩块4~7转角及位移曲线

(c)岩块8~10转角及位移曲线
综上所述,各岩块所处状态的判别依据如下。
(1)稳定状态:当块体底边与水平面夹角小于等于25.5°,任意时刻位移小于0.02 m。
(2)滑动状态:当块体底边与水平面夹角小于等于25.5°,任意时刻位移大于0.02 m。
(3)倾倒状态:当块体底边与水平面夹角大于25.5°,任意时刻位移小于等于0.02 m。
(4)滑动-倾倒状态:当块体底边与水平面夹角大于25.5°,任意时刻位移大于0.02 m。
2.2 坡体岩块分区及分区特征
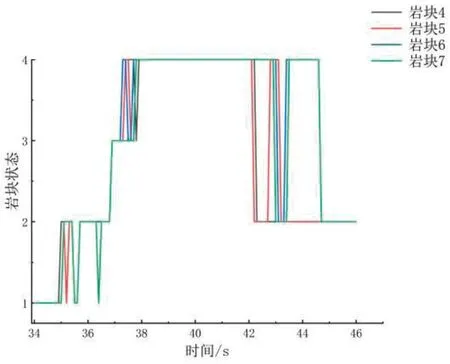
地震作用下各岩块的状态随时间变化情况如图8所示(图中纵轴数字“1”代表稳定,“2”代表滑动,“3”代表倾倒,“4”代表倾倒-滑动)。各岩块状态通常在稳定、滑动、倾倒、滑动-倾倒状态之间转换,尤其以滑动-倾倒状态与滑动状态之间的转换最为显著。可以看出随着岩块所处位置越高,岩块状态转换越快。根据岩块从稳定状态到滑出坡体所经历的状态变化及状态持续的时间,本文将坡体上岩块进行分区,分为底部(岩块1~3)、中部(岩块4~7)、顶部(岩块8~10),岩块分区情况及第38、40、42秒时各岩块状态如图9所示。

(a)岩块1~3
(b)岩块4~7

(c)岩块8~10
编号1~10岩块滑出坡体的时间分别为38.9,39.5,41,41.8,42.2,43.2,44.3,45.5,46.9,51 s。底部岩块主要经历稳定、滑动、倾倒及滑动-倾倒的过程,各岩块不同状态之间时间间隔明显,状态转换慢,其中倾倒-滑动状态保持时间较长,并以倾倒-滑动状态滑出坡体;中部岩块主要经历稳定、滑动、倾倒及滑动-倾倒再到滑动的过程,各岩块在稳定与滑动、倾倒与滑动-倾倒、滑动-倾倒再到滑动间相互转换,且状态转换较快,并最终以滑动状态滑出坡体;顶部岩块主要经历稳定、滑动、倾倒及滑动-倾倒再到滑动的过程,各状态间持续时间短,状态转换快,且大部分时间处于滑动-倾倒再到滑动的过程,并最终以滑动状态滑出坡体。

(a)第38秒

(b)第40秒
(c)第42秒
可以看出,从坡体底部到顶部,岩块状态在地震作用下转换越来越快,这与岩块所处的位置及岩桥的长度有关,且除底部区域外,中部与顶部区域岩块最终均以滑动状态滑出坡体。同时,根据图8数值模拟结果发现,与各岩块状态随时间变化相吻合,说明了岩块状态判别依据的正确性。此外,从各岩块滑出坡体的时间来看,坡体上的岩块在地震作用下依次滑出坡体,且坡体底部、中部岩块滑出的时间间隔较短,顶部岩块滑出坡体时间间隔较长,特别是顶部岩块9、10滑出坡体时间间隔为4.1 s,说明地震作用下坡体底部与中部岩块运动速度较快,稳定性差,顶部岩块运动速度较慢,稳定性强。
2.3 坡体岩块失稳时间点选取
根据Goodman等[3]研究表明,坡底第1个岩块稳定性对上部岩块稳定性有至关重要的影响,因此,通过监测岩块1质心处位移,得到岩块1在整个地震作用过程位移图如图10所示。

(a) 0~170 s水平位移

(b)32~37 s水平位移
由图10可以看出,岩块1在地震过程中经历了位移启程、位移累积、位移稳定(失稳)3个阶段。其中,位移启程发生在第35秒,在这一时间点往后岩块1水平位移显著增加。因此,各岩块取岩块1位移启程前1 s(即第34秒)到各岩块滑出坡体这段时间来研究岩块位移与底边转角的关系,从而给出岩块破坏模式的判别依据。此外,根据坡体上岩块1失稳时间点,地震对坡体稳定性的影响具有一定的滞后性。
由图7可以看到,底部和中部岩块在34~35 s转角有波动,但岩块整体仍处于稳定状态,直至岩块滑动为止。而中部岩块转角的波动要比底部岩块剧烈,顶部岩块仍保持稳定状态,这可能与岩块的长细比与所处位置有很大的关系。Chen等[11]认为在地震作用下长细比最大的岩块(中部)会最先移动,且对坡体稳定性有至关重要的影响。因此,对于坡体中部岩块长细比对坡体稳定性影响规律及影响范围需要进一步探究。
3 结论
本文运用UDEC离散元数值模拟软件,揭示了地震过程中坡体上各岩块从稳定到滑出坡体时间段内所处的状态,并根据所处的状态进行了分区,对分区特征及破坏模式进行了研究。结论如下:
(1)根据数值模拟的结果,本文提出了一种以位移量及转角大小对地震作用下岩块运动状态进行判别的依据,可用于确定各岩块在地震作用下随时间变化的状态。
(2)坡体上各岩块在地震作用下一般会处于稳定、滑动、倾倒、滑动-倾倒这4种状态,其中,坡体底部岩块主要以滑动和滑动-倾倒为主,坡体中部与顶部主要以滑动-倾倒转为滑动为主,且坡体中越往上的岩块,其滑动-倾倒到滑动状态转换越快。
(3)根据坡体上岩块滑出坡体的时间点,在地震作用下,坡体发生整体失稳,岩块依次滑出坡体,其中底部与中部岩块运动速度快,顶部岩块运动速度慢。

