多径异步LSC-DS-CDMA信号伪码估计

潘微宇，赵知劲,2

(1.杭州电子科技大学 通信工程学院，浙江 杭州 310018； 2.中国电子科技集团第36研究所 通信系统信息控制技术国家级重点实验室，浙江 嘉兴 314001)

0 引 言

直扩码分多址(direct sequence code division multiple access，DS-CDMA)具有较强的抗干扰性和保密性，已被广泛应用于军事和民用通信中[1,2]。在非合作通信中，接收方要完成对截获信号的解调，需要已知所用扩频码序列，因此，对DS-CDMA信号伪码盲估计的研究具有重要意义。

目前对于长码和短码DS-CDMA信号伪码估计的研究已有一些相应研究成果。文献[3,4]分别利用无监督学习神经网络和平行因子法完成了短码DS-CDMA信号的伪码估计。文献[5]将长码DS-CDMA信号构建为缺失数据的短码DS-CDMA张量模型，并结合重叠窗法进行分段，利用嵌套迭代最小二乘投影插补法估计异步长码DS-CDMA信号的伪码。文献[6]利用多天线接收信号，将长码DS-CDMA信号构建为短码DS-CDMA子张量，并使用变步长梯度下降法对子张量进行Tucker分解，得到各用户的伪码，估计性能比插补法更优。文献[7]在文献[6]的基础上，使用交替最小二乘法对各子张量进行CP(canonical polyadic)分解得到各用户伪码，再利用库搜索提高估计精度后，性能优于文献[6]。对于短码扩频长码加扰的LSC-DS-CDMA信号的伪码估计，相关研究较少。文献[7]的库搜索无法用于LSC-DS-CDMA信号。文献[8,9]在FastICA和m序列三阶相关函数特性基础上，分别结合矩阵填充法和分圆陪集理论估计LSC-DS-CDMA信号各用户复合码，再利用相关运算估计长码和短码，但矩阵填充法对噪声敏感，三阶相关特性在低信噪比下也难以获得准确峰值。上述文献均讨论在理想信道下DS-CDMA信号伪码的估计，而实际通信中大多都是多径环境[10,11]。文献[12]在文献[5]模型的基础上，使用正则最小交替二乘法估计多径环境下长码DS-CDMA信号伪码，但其将多径视作干扰，没有解决多径干扰对伪码的影响，估计性能不佳。文献[13]基于最大似然准则(maximum likelihood，ML)联合估计单用户长码直扩信号伪码和多径信道，但不能直接应用于LSC-DS-CDMA信号的伪码估计。

针对多径环境下异步LSC-DS-CDMA信号伪码估计问题，采用重叠窗对信号进行分段并构建子张量，利用动量梯度下降法和改进线性搜索步长算法对各个子张量进行Tucker张量分解估计复合码，在提高复合码估计准确率的同时，大大减少迭代次数，然后对含有多径干扰的各用户复合码和多径信道进行ML联合估计，最后利用梅西算法和相关运算得到各用户的长码和短码。

1 多径异步LSC-DS-CDMA信号的TUCKER张量模型构建

设有U个用户，用L根天线接收信号，且各用户之间相互独立，扩频码和长扰码的周期已经估计得到，则第l根天线接收到的多径LSC-DS-CDMA信号通过扩频码码片速率采样后基带信号可以表示为

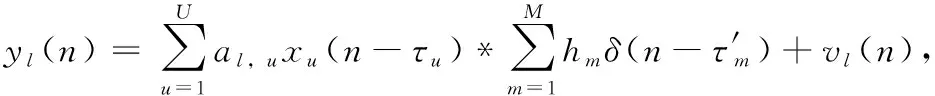
(1)

对于异步多径LSC-DS-CDMA信号，各用户主径失步时间均不相同，若使用一倍扩频码周期进行分段，会导致不同用户的每段信号a中包含的信息码完整性不同而无法估计伪码。因此本文按照2倍扩频码周期对接收信号进行重叠一半分段，对第w段信号，当w=jQ-1,j=1,2,…J时，使用长为(2Nb-1)的时间窗进行分段，对于其余段信号，利用长为2Nb的时间窗对信号进行分段，共得到W段信号。

则第l根天线接收信号的第w段信号可表示为

(2)

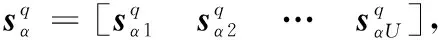
(3)

(4)

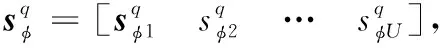
(5)

(6)

(7)

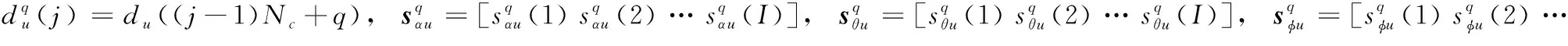
(8)

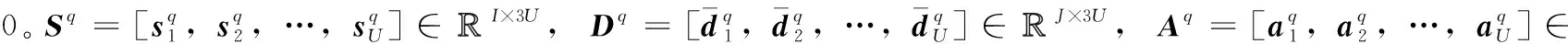
(9)

2 基于动量梯度下降法和改进线性搜索步长的复合码片段估计

由于张量Tucker分解具有唯一性，对式(8)分解得到的因子矩阵分别对应各用户的复合码片段、信息码片段和接收增益矩阵。定义张量最优化分解的目标函数为

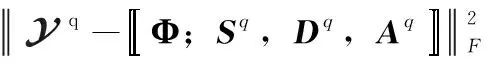
(10)

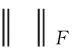
(11)

(12)

(13)

(14)

基于动量梯度下降的3个因子矩阵Aq，Sq，Dq的第k次更新公式为

Aq(k)=Aq(k-1)+μ(k)[λV(k-2)+(1-λ)G1(k-1)]
Dq(k)=Dq(k-1)+μ(k)[λV(k-2)+(1-λ)G2(k-1)]
Sq(k)=Sq(k-1)+μ(k)[λV(k-2)+(1-λ)G3(k-1)]

(15)

其中，μ(k) 为第k次迭代的实际步长，V(k)=λV(k-1)+(1-λ)Gi(k),i=1,2,3为动量项，λ为动量系数，引入动量项可提高收敛速度。

步长一般通过经典的线性搜索算法确定，但是该算法每次把步长初始化为一个固定值，这使得每次迭代的实际步长和初始步长的误差均与下一次迭代的初始步长无关。由于这个误差越大，会导致步长的搜索次数越多，从而影响收敛速度。因此，提出一种改进的线性搜索算法，利用上一次搜索的实际步长和初始步长的误差值来确定下一次的初始步长，大大减少搜索次数，进一步提高算法的收敛速度。改进的线性搜索步长算法如下：

(1)步长初始化为μ0(k)=1；

(2)计算误差函数f(Aq,Sq,Dq)，μ1=μ0(k)；

(3)当f(Aq+μ1G1,Dq+μ1G2,Sq+μ1G3)>f(Aq,Sq,Dq) 时，μ1=β1μ1，β1∈(0,1) 为固定参数；否则，循环结束，得到本次迭代的实际步长μ(k)=μ1。

(4)利用上次搜索的初始和实际步长，确定下次迭代的初始步长μ0(k+1)=(μ0(k)-β2μ(k))/(1+β2)，β2∈(0,1) 为固定参数。返回步骤(2)。

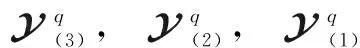
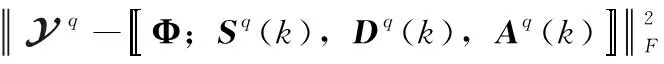
(16)

当f(k)-f(k-1)<β3(β3是一个极小的数)或者当迭代次数k达到最大值时，迭代结束。

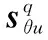
(17)

(18)

3 伪码和多径信道联合估计

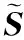
(19)

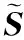
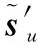
(20)

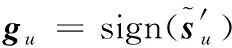
(21)

其中，0τ′m×1为τ′m×1维的零向量。由式(20)可见，h是待估计的多径信道矩阵，Pu中包含了待估计的伪码信息。

3.1 多径信道估计

(22)

基于最大似然准则求解Pu和h，可等价为求下式的优化问题

(23)

首先仅考虑求解连续变量h。假设离散变量Pu已知，上式即为一个最小二乘问题，可求得

(24)

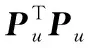
3.2 伪码估计

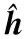
(25)

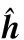
(26)

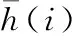
(27)

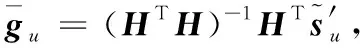
(28)

(29)

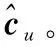
(30)

至此，U个用户的长码和短码序列已经全部完成估计。

4 仿真分析

实验1：用户数与天线数对长短码估计性能的影响

取莱斯因子K=5，短码周期Nb=64，长扰码周期Nc=255，用户数U=2,3，天线数L=8,9，本文算法对长短码估计的误码率曲线如图1所示。

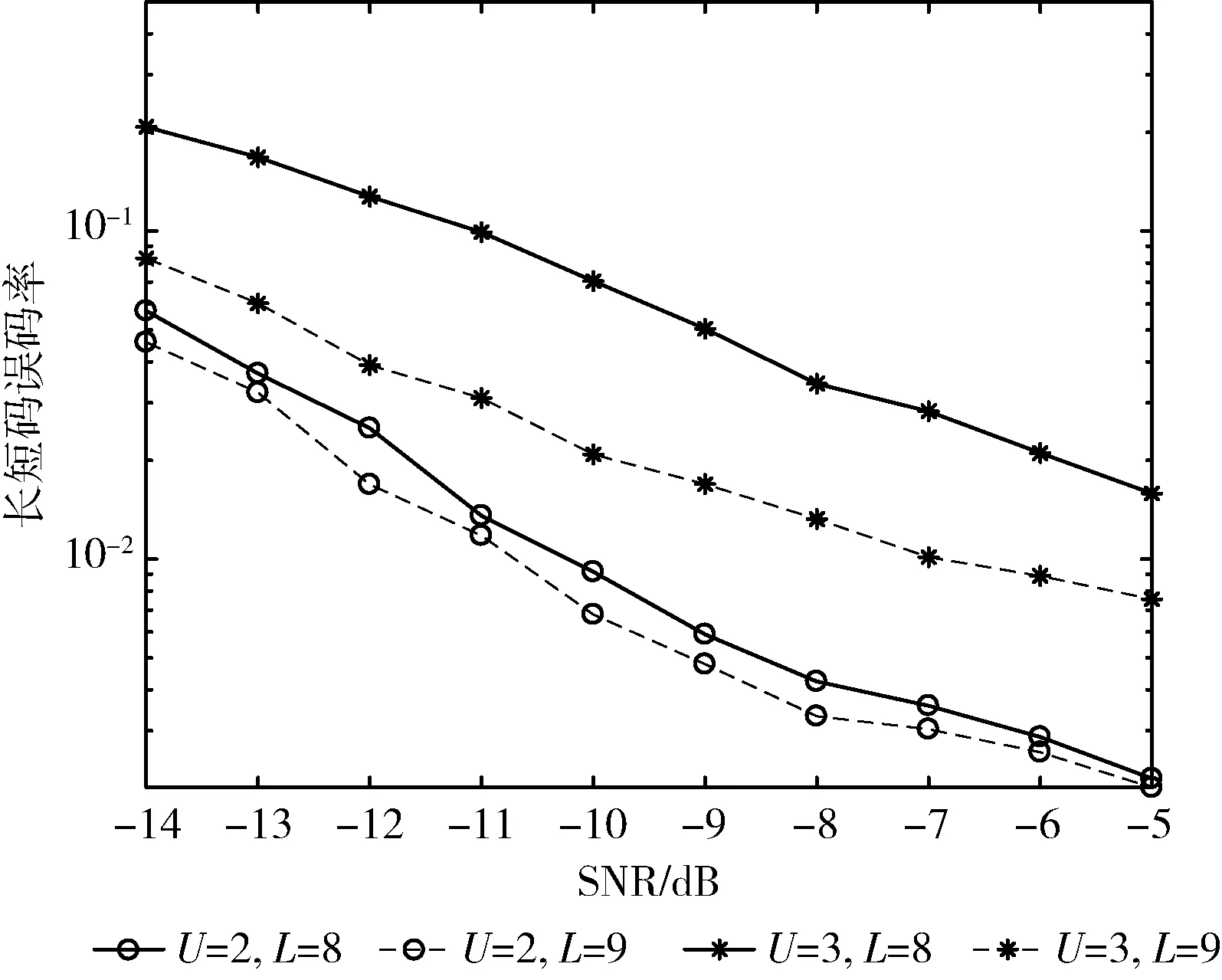
图1 用户数和天线数对估计性能的影响

由图1可知，当接收天线数固定时，用户数越多，长短码的估计性能越差，这是由于用户数越多，导致各用户间的干扰也越大，从而影响估计性能；当用户数固定时，天线数越多，长短码估计性能越好，这是因为天线数越多，则接收到的可利用信号越多，估计误差也就越小。当L<3U时无法使用HOSVD初始化张量分解的因子矩阵，因此在实验中利用随机生成的(3U-L)维矩阵和L维左奇异向量矩阵拼接构成的矩阵初始化因子矩阵，估计性能有明显下降。

实验2：短码周期和长扰码周期对长短码估计性能的影响

取莱斯因子K=5，天线数L=9，用户数U=3，当Nc=255，Nb=32和Nb=64以及Nc=511，Nb=32和Nb=64时，本文算法对长短码估计的误码率曲线如图2所示。

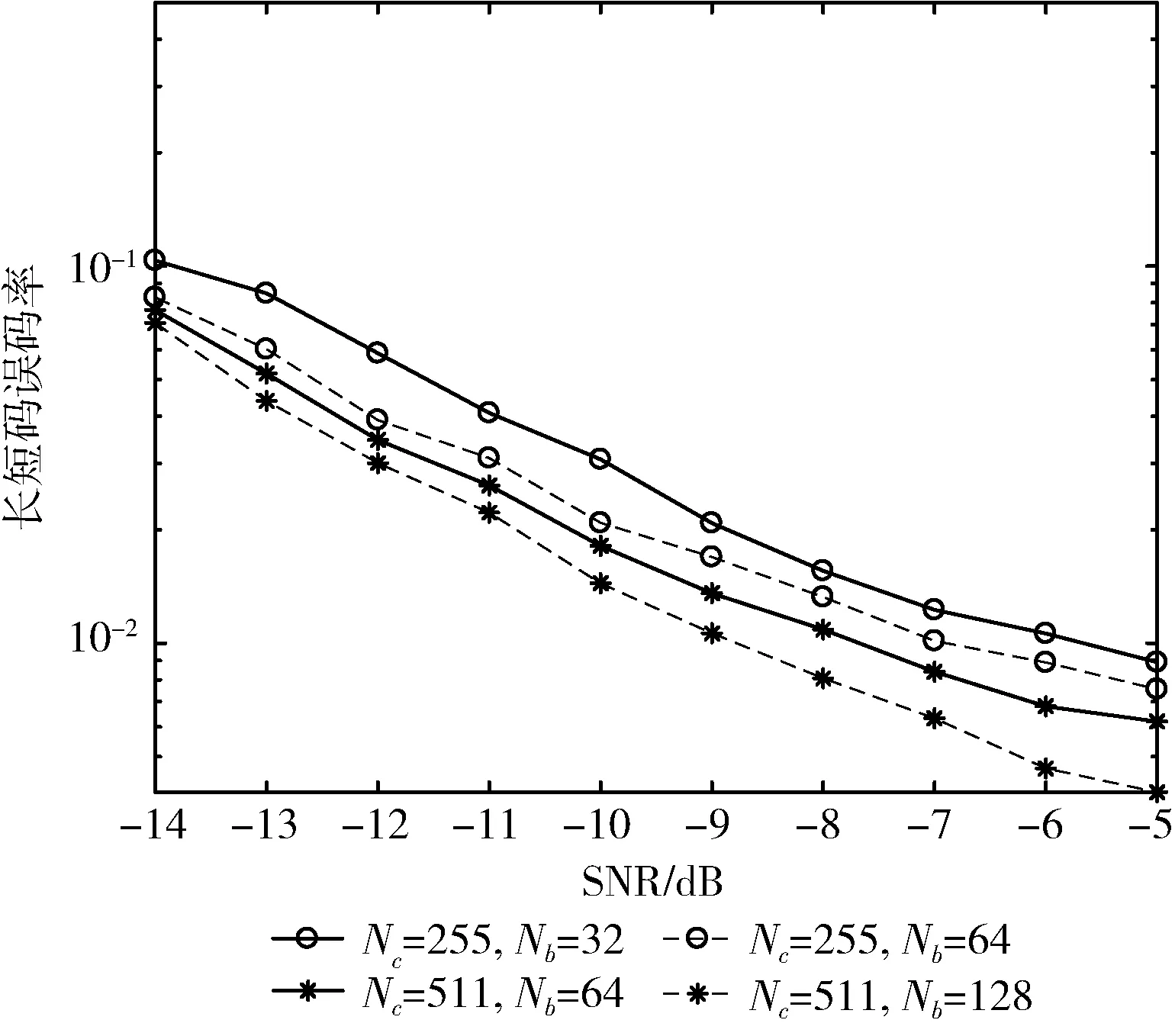
图2 扩频码周期和长扰码周期对估计性能的影响

由图2可知，当长扰码周期长度固定时，扩频短码周期越大，估计性能越好，这是因为分割的子张量越少，所需估计的伪码片段就越少，产生的误差也就越少，因此误码率就越小。当分割的子张量数目相同时，长扰码周期长度越长，估计性能越好，这是由于长扰码周期越长，梅西算法可处理的数据更多，对长扰码的估计越准确，因此估计性能越好。

实验3：ML联合估计算法对复合码估计性能的改善。

取莱斯因子K=1.25,5,10， 天线数L=9，用户数U=3，短码周期Nb=64，长扰码周期Nc=255，本文算法对复合码估计的误码率曲线如图3所示。

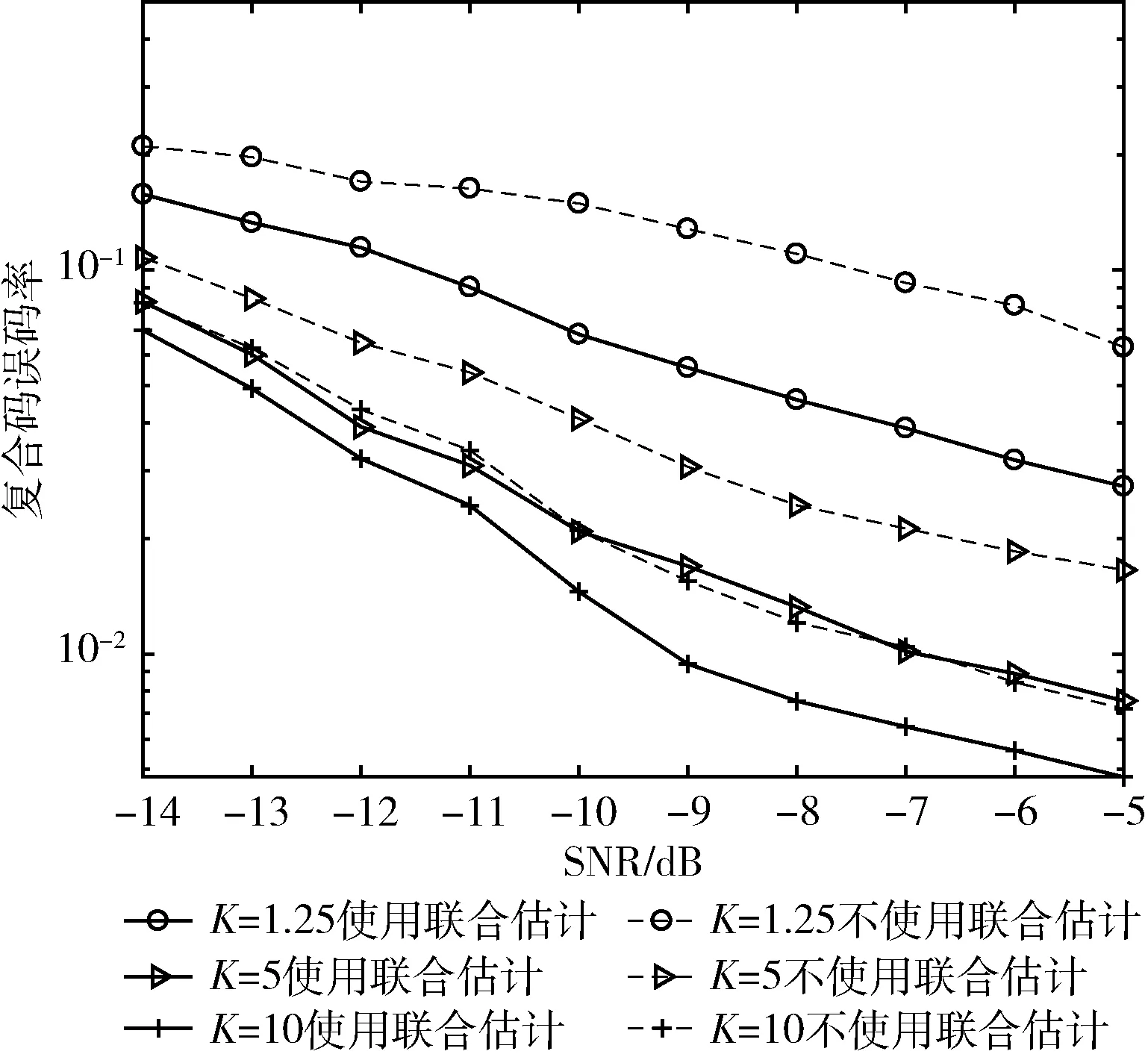
图3 莱斯因子与联合估计对复合码估计性能的影响

由图3可知，随着莱斯因子逐渐增大，算法对复合码的估计性能越好，这是由于莱斯因子越大，信号中主径分量越强，其余径分量越弱，多径影响减弱，估计性能也就越好；当莱斯因子K分别为1.25、5和10时，使用ML联合估计算法比不使用该算法的复合码估计性能提升分别约5 dB、4 dB、3 dB，莱斯因子越大，ML联合估计算法对复合码的估计性能提升越小。

实验4：算法性能对比

取莱斯因子K=5，天线数L=9，用户数U=3，Nb=64，Nc=255，本文算法、文献[6]、文献[7]与文献[12]的复合码估计的误码率曲线如图4(a)所示，迭代次数如图4(b)所示。

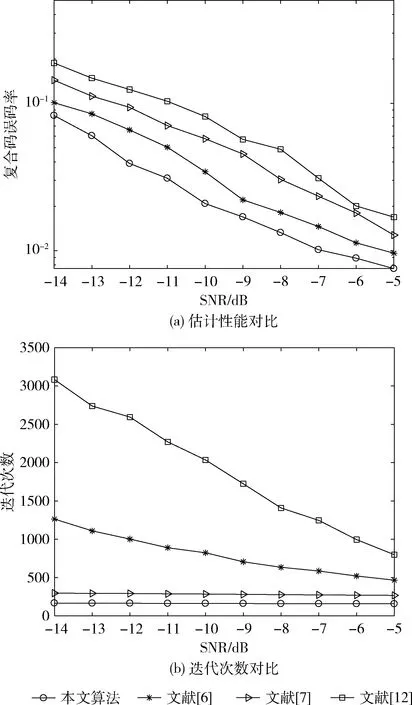
图4 本文算法与对比算法的估计性能和迭代次数

由图4(a)可知，本文所使用的算法估计性能最佳，文献[6]算法次之，文献[12]算法性能最差，这是因为本文算法和文献[6]、文献[7]均使用张量分解，避免了对数据的插补，估计性能均优于文献[12]，本文使用动量梯度下降法，相比于文献[6]的经典梯度算法，性能有所提升；文献[7]的CP分解性能比Tucker分解的差，并且多项式库搜索无法适用于本文所提的复合码，在实验中没有使用库搜索，因此性能不佳。由图4(b)可知，本文算法迭代次数最少，文献[7]算法迭代次数次之，文献[12]算法迭代次数最多，且前两种算法迭代次数几乎与信噪比无关。这是因为本文算法改进了线性步长搜索算法，大大减少了迭代次数，文献[12]由于插补法误差较大，导致迭代次数增加。

5 结束语

针对多径环境下的异步LSC-DS-CDMA信号的伪码盲估计问题，本文先利用重叠窗分段信号并构建成Tucker张量模型，利用改进的线性搜索步长结合动量梯度下降法来估计因子矩阵，然后利用接收增益因子矩阵的互相关性和移位相乘分别解决排序和幅度模糊问题，使用ML准则对复合码和多径信道进行联合估计。最后利用梅西算法和相关运算得到各个用户的长扰码和扩频码。仿真实验结果表明，本文算法在估计性能和收敛速度上都优于现有算法。