对“一道高考圆锥曲线题中的定点问题”再探究
2023-01-16 02:24聊城大学数学科学学院252000徐茂林房元霞
中学数学研究(江西) 2023年2期
聊城大学数学科学学院 (252000) 徐茂林 房元霞
一、原题呈现
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
二、文献[1]中的结论
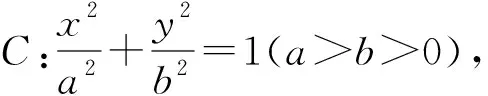


两条直线恒过圆锥曲线上的固定点,如果这个点是圆锥曲线上任意一点,会有一般的结论吗?带着这个问题,我们先用GeoGebra软件进行了探索,归纳出一般结论后再例行证明,如下是我们探究的结论.
三、再探究
(一)椭圆的情形
综上所述,于股骨头坏死的临床诊断工作当中,积极采用磁共振技术,可显著提高患者病情确诊的几率,让患者能够及早接受对症治疗,从而有助于减少其致残的风险,提高生活质量,建议在临床上进行推广和使用。
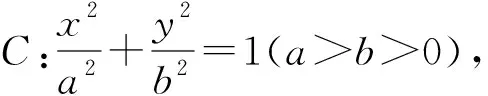

图1
本文仅以焦点在x轴上的圆锥曲线为例进行证明,其他对称情形不再累述.
证明:由题意,直线AP、AQ的斜率都存在,且直线l不经过点A(x0,y0).


(二)双曲线与抛物线的情形


图2


图3

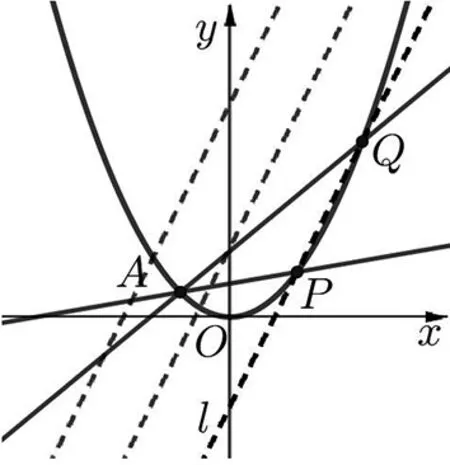
图4
抛物线(焦点在y轴)的这种特殊情况,因异于文章研究内容,仅予以说明,感兴趣的读者可自证.证明方法可参考定理1的证明;读者亦可用焦点在y轴上的圆锥曲线统一方程来寻求原因.
既然三种圆锥曲线中都有一般的公式,圆锥曲线有运用离心率的统一定义、方程,如果从统一的角度进一步考虑这个问题,我们坚信:应该会有统一的结论.
(三)圆锥曲线的一般情形
根据圆锥曲线的统一方程:(1-e2)x2+y2-2pe2x-p2e2=0(当0


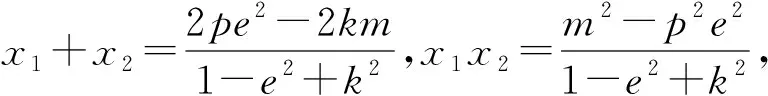
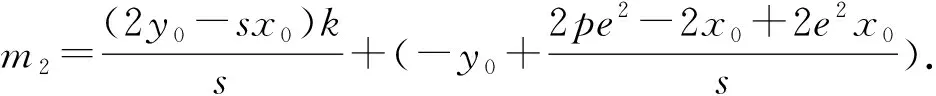
且可以容易计算得到:

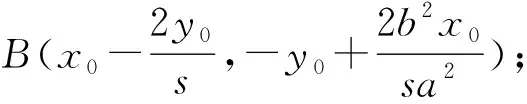

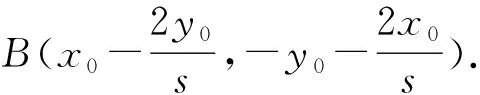
猜你喜欢
小资CHIC!ELEGANCE(2022年1期)2022-01-11
数学物理学报(2020年4期)2020-09-07
公民与法治(2020年12期)2020-07-25
公民与法治(2020年4期)2020-05-30
南方周末(2018-03-08)2018-03-08
科学中国人(2017年22期)2018-01-02
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
公民与法治(2016年9期)2016-05-17
摄影之友(2016年8期)2016-05-14
中学数学杂志(2015年9期)2015-01-01

