2022年全国理科甲卷第23题的多解及推广

四川师范大学数学科学学院 (610068) 谢志强 杨 志 四川省什邡中学 (618499) 纪定春

1 试题呈现

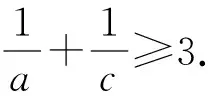
2 试题多解

2.1 问题(1)的多解

解法1：(柯西不等式法)高中数学选修4-5定义了柯西不等式，若a1，a2，b1，b2都是实数，则(a12+a22+a32)(b12+b22+b32)≥(a1a2+b1b2+a3b3)2，当且仅当ai=kbi时等号成立.由柯西不等式有(a2+b2+4c2)(12+12+12)≥(a+b+2c)2.因为a2+b2+4c2=3，所以a+b+2c≤3.

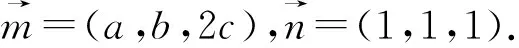
解法3：(构造函数法)考虑构造二次函数f(x)=(a2+b2+4c2)x2+2(a+b+2c)x+3，显然可得f(x)=(ax+1)2+(bx+1)2+(2c+1)2≥0.由于这个二次函数大于等于零恒成立，所以判别式△≤0，故△=4(a+b+2c)2-4(a2+b2+4c2)·3≤0，化简后可得a+b+2c≤3.

解法4：(二元均值不等式法)因为(a+b+2c)2=a2+b2+4c2+2ab+4ac+4bc=3+2ab+4ac+4bc，由二元均值不等式可知a2+b2≥2ab，a2+4c2≥4ac，b2+4c2≥4bc.因此，(a+b+2c)2≤3(a2+b2+4c2)=9，故a+b+2c≤3.

解法5：(作差法)考虑将不等式两边同时平方后再作差，问题化为证明9-(a+b+2c)2≥0成立.因为9-(a+b+2c)2=3(a2+b2+4c2)-(a+b+2c)2=2a2+2b2+8c2-2ab-4ac-4bc=(a-b)2+(b-2c)2+(2c-a)2≥0，即a+b+2c≤3.

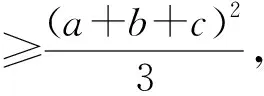
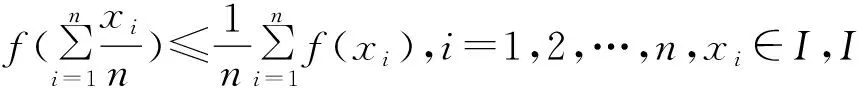
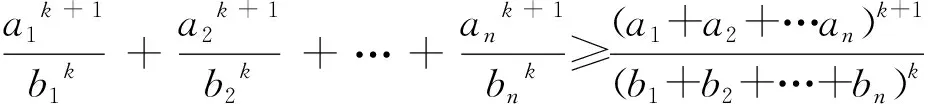
解法11：(判别式法)令a+b+2c=t，a2+b2+4c2=3，联立可得a2+b2+(t-a-b)2=3，展开后整理可得2a2+a(2b-2t)+2b2+t2-2tb-3=0.由于方程有解，故△1=-3b2+2bt-t2+6≥0，即-3b2+2bt-t2+6≥0.再由△2=(2t)2-4×(-3)·(6-t2)≥0，可得t2≤9，故t≤3，即a+b+2c≤3成立.

2.2 对问题(2)的多解

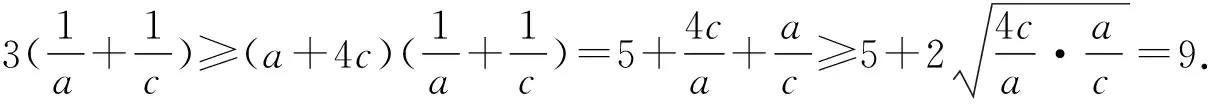
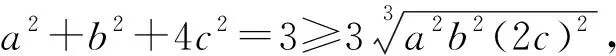
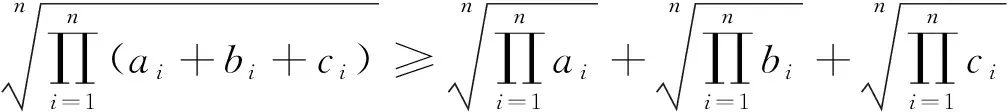
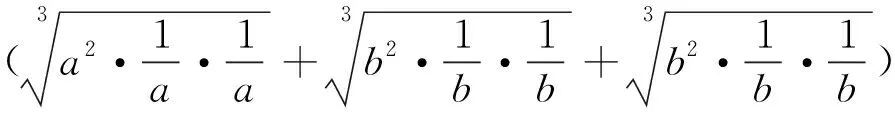
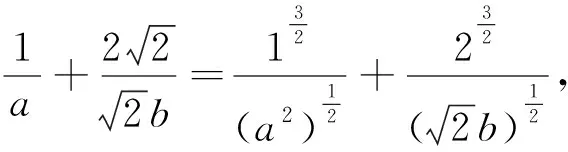
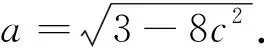
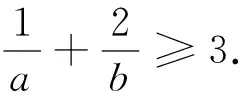
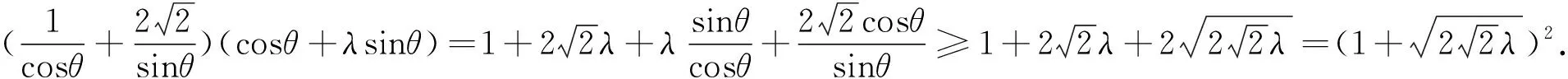
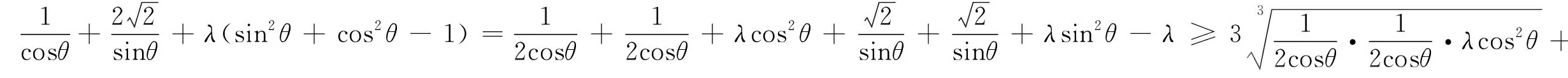
3 试题的推广

3.1 对问题(1)的推广

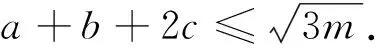
评注：该推广是将原问题中的3推广为m，证明方法同解法1.

推广2已知a，b，c均为正数，且a3+b3+(2c)3=3，证明：a+b+2c≤3.

评注：此推广将原问题中字母次数推广，即2次推广为3次，证明方法同解法7.

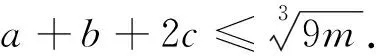
评注：此推广是将条件中的2次，推广为3次，常数3推广为m，证明同解法7、8.

评注：此推广是将原问题中的常数3推广为m，且字母由原来的2次，推广为n次.

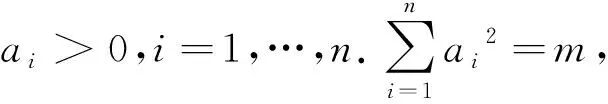
评注：该推广将条件中元的个数推广为n个，证明方法同解法1.

评注：该推广将条件中元的个数推广为n个，次数也推广为n次，证明方法同解法7和解法8.

3.2 对问题(2)的推广

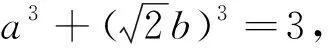
评注：该推广是将条件中的次数推广为3次，证明方法，可以运用权方和不等式.

评注：该推广是将条件中的次数推广为n次,其证明方法还是可以运用权方和不等式.

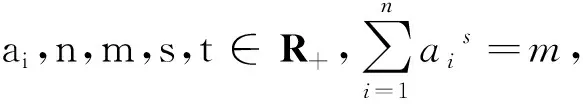
评注：该推广是推广2中元的个数由2元推广到n元.

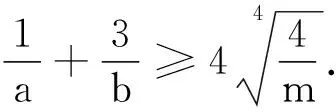
评注：该推广是将问题2中次数推广到3次.

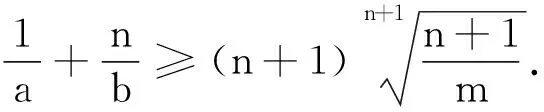
评注：该推广是将推广4中的次数推广到n次.

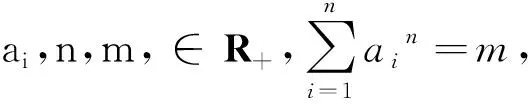
需要注意的是，上述推广内容，不一定全部适用于高中学生，而是需要根据学生的学习情况，有选择性的将上述推广纳入数学课堂教学使用.