关注错误资源,还原生态课堂
——一道函数零点习题的纠错教学
宁夏彭阳县第三中学 (756599) 韩连嵩
建构主义认为,学习就是学生认知结构变化的过程,是学生主动建构的过程,学生在已有认知结构的基础上,经过认知冲突、同伴讨论、思考辨析的学习才是真实的学习.因此,课堂教学中教师要善于关注错误资源,还原生本课堂,要留给学生足够的思考辨析时间和充分探讨的空间,使他们在知错、议错、纠错中达到触类旁通,促进深度学习.
一、探究的缘由:殊途不同归
题目(2021年贵州适应性测试)已知函数f(x)=x+1-xex.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)判断f(x)是否有零点,若有,求出零点的个数;若没有,请说明理由.
这是笔者复习函数零点时,从复习材料中选取的一道习题,对于第⑴小题学生都能轻松的解决,得到的切线方程为y=1,过程略.但对第⑵小题,学生经过尝试给出了如下的解法:

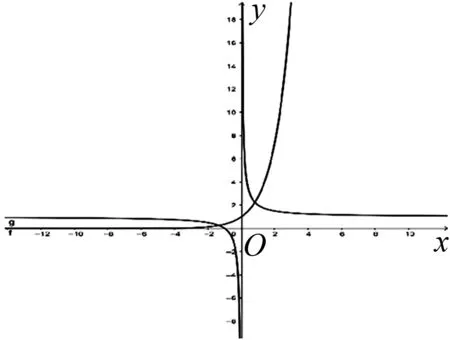
图1

学生甲提出了疑义,学生乙又说参考答案也是这样解的,全班同学哗然,不知所措,笔者也被这节外生枝的举动,迎头一棒,心想难道是题目错误还是参考答案错误,但静下心来仔细琢磨,终于发现了问题的症结,那就是学生对研究函数问题定义域优先的原则理解不透彻.何不借此机会将问题抛给学生,让学生进行交流探究呢?于是,笔者改变了原有的教学预设,把课堂还给学生,让位于学生,不曾想却得到了满意的收获.
二、课堂探究:百花齐争艳
1.议错纠错,不甘示弱
师:大家对学生甲的解答(参考答案的解答)有什么看法?
(问题抛出后,同学们讨论很激烈,原生态的课堂气氛非常浓厚,有部分同学认为甲的解答过程思路是正确的,也有部分同学认为甲的解答过程有问题,但一时看不出错在什么地方?当学生思维受阻时,教师适时诱导,启发学生观察思考)
追问:你能否借助于图来检验甲同学解法思路的正确性?
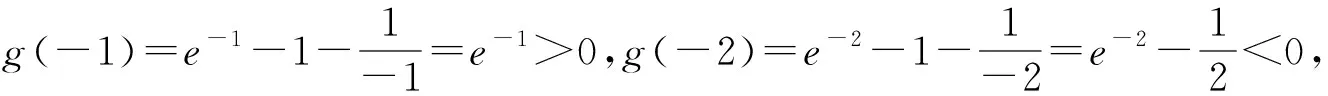
师:很好.生1通过观察,利用函数零点存在性判定定理检验了甲同学的解答有问题,还有其它意见吗?
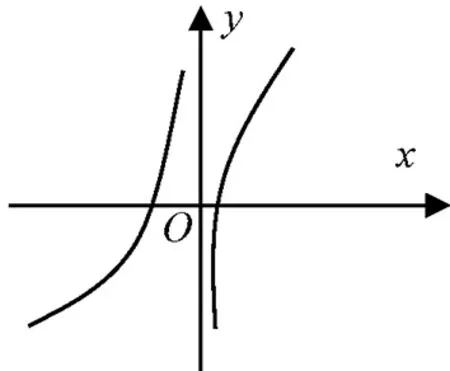
图2
(同学们对生1、生2的方法表示赞同,平时细心的生突然举手示意)
生3:生2画出的图象不够准确规范,画函数图象应该考虑区间端点处函数值的变化趋势.当x→-∞时,g(x)→-1,画出函数g(x)的图象应该是图3所示.
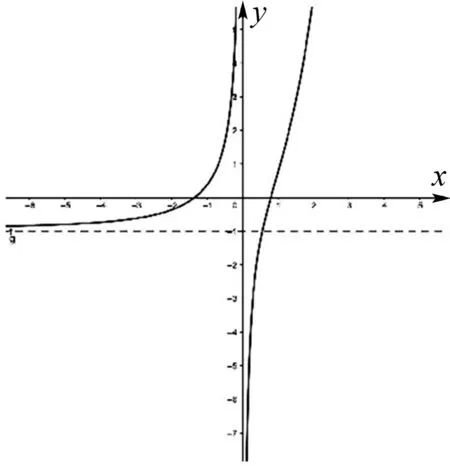
图3
(同学们表现都很积极,能从不同的角度发现甲同学解答出现的纰漏,特别是生3给我们指出画函数图象时,要考虑周全,关注一些间断点和区间端点处函数值的变化趋势,才能画出准确规范的图象,助于问题的分析与解决)
师:通过大家的交流讨论,认为甲同学的解答(参考答案)有纰漏,那么你能指出指出其中的问题并进行修正吗?
(问题抛出后,同学们争先恐后,抢着举手示意,课堂气氛格外活跃)
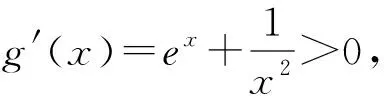
师:解决函数问题时,我们常常用导数来研究函数的性质,定义域优先是我们首先要考虑的.图象的直观性可以帮助我们分析思考问题,画函数图象时,一定要关注间断点,弄清定义区间端点处函数值的变化趋势,画出比较准确规范的图象.
2.解法探究,百花齐放
师:上面的解法都是将函数f(x)的零点问题等价转化为方程f(x)=0的根的问题,然后给方程两边同除以x后构造函数来解决的,那么,能否不用除以x,直接从函数的解析式入手解决问题呢?请大家思考尝试.
(问题抛出后,同学们思考交流、尝试探讨,稍等片刻,便有同学登台亮相,相继展示其解法)
生4:f′(x)=1-(x+1)ex,设g(x)=f′(x),于是g′(x)=-(x+2)ex,令g′(x)=0得x=-2.当x∈(-∞,-2)时,g′(x)>0,g(x)单调递增;当x∈(-2,+∞)时,g′(x)<0,g(x)单调递减,所以g(x)在x=-2处有极大值,且极大值g(-2)=1+e-2>0.又当x→-∞时,g(x)→1,且g(0)=0.因此当x∈(-∞,0)时,g(x)=f′(x)>0,函数f(x)单调递增;当x∈(0,+∞)时,g(x)=f′(x)<0,函数f(x)单调递减,且当x→-∞时,f(x)→-∞,f(0)=1,当x→+∞,f(x)→-∞.所以函数f(x)有两个零点.
生5:函数f(x)的零点⟺f(x)=0⟺xex-x=1⟺g(x)=xex-x与h(x)=1图象交点.研究函数g(x)的性质同生4,其图象如图4所示,由图象可知,函数f(x)有两个零点.

图4
生6:函数f(x)的零点⟺方程xex=x+1的根⟺函数g(x)=xex与h(x)=x+1图象的交点.因g′(x)=(x+1)ex,令g′(x)=0得x=-1.当x∈(-∞,-1)时,g′(x)<0,函数g(x)单调递减;当x∈(-1,+∞)时,g′(x)>0,函数g(x)单调递增,且极小值f(-1)=-e-1<0,当x→-∞时,g(x)→0,在同一坐标系中画函数g(x)与h(x)的图象,如图5所示.由图象可知,函数f(x)有两个零点.

图5
师:大家思维敏捷、建言献策,真可谓百花争艳满堂香.本题开始的解法和生6的解法可以说是简洁明了,但老师心中有个疑点:这种解法是否具有普适性?请大家用这种方法来研究下面问题.

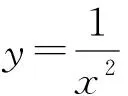
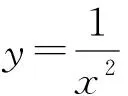
(大家表示赞同)
师:很棒!你帮老师解决了心中的疑点,同时也提醒大家在研究函数零点问题时,转化成两图象交点的策略要因题而论.
3.变式探究,思维升华
师:请同学们继续研究下面的问题.
问题1 讨论函数f(x)=ax+1-xex的零点个数.
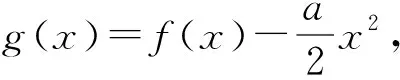
(学生练习,教师巡回指导,约3分钟,绝大部分学生都已正确的完成解答,指派代表展示)


图6
①当a≤0时,h′(x)>0,函数h(x)单调递增,则函数h(x)不可能由两个不同的零点;
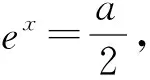
师:两位同学给大家分别展示了参数分离法和分类讨论法的解题策略,思路清晰、方法得当.参数分离法和分类讨论法是求解含参数零点问题的主要方法,希望同学们在平时的学习中加以理解和体会.
三、教学感悟
1.数学教学要重视学生基础性知识
重视基础知识教学,是纠错教学的前提.学生对基础知识理解不到位,会导致思维方法不正确,造成解题失误,甚至会出现错误.只有夯实基础知识、理解基本概念、掌握基本方法,才能降低失误,克服“懂而不会”,“ 会而出错”的现象.数学教学中,教师应该重视学生基础性知识,帮助学生分析基本概念的形成原理,通过长期的基础性知识教学,就有可能使学生少出错误或不出错误.
2.还原生态课堂,重视学生提出的问题
传统的数学课堂教学教师讲授多、学生体验少、缺乏课堂生机,不把时间还给学生,生怕完成不了课堂任务;不愿意把思考的机会让给学生,担心学生的思维出“差错”,追问出“岔道”,影响原本预设好的教学轨迹,殊不知学生提出的问题比教师提出的问题更具有针对性,只有学生提出的问题才是学生学习的原发动力;把时间还给学生,把机会让给学生,因为教学的根本目的是发展学生.教师要领悟新课改精神,处处为学生着想,让位于学生,让学生成为课堂的真正主人,还原生态课堂.只有这样,教学才能“放马于原野之中,牵其于晚霞之时”的潇洒境界,演绎出精彩课堂.
3.善待错误资源,重视纠错教学
教学的重要任务之一就是释疑解惑.学生所犯的错误往往都是我们课堂教学的缺失,教师要善待错误.学生的错误资源是纠错教学的一手材料,学生有失误甚至犯错误,就说明他们有疑问、有困惑.疑问不解,困惑不除,不管教师如何引导他们学习正确的方法思路,学生终究还会出错.课堂教学中只要教师利用好这些错误资源,帮助他们分析错误缘由,形成知识整体观的认知,促进深度理解,才能把他们引入到正确的思路上,合理的方法上来,给学生留下深刻的印象,才能避免以后不会出现类似的错误或失误.

