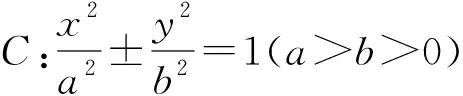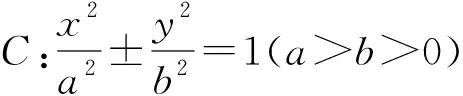对2022年全国新高考Ⅰ卷22题Ⅱ问的探究*

四川省内江市开放大学中学部 (641100) 严豪东 内江师范学院数学与信息科学学院 (641100) 刘成龙

一、试题再现

(Ⅰ)求l的斜率;

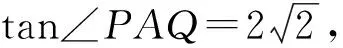
本题以双曲线为载体,主要考查解析几何中的设线、解点与面积计算.该试题内涵丰富,解答入口宽,是考查学生运算能力、推理能力等学科素养的良好载体.

二、试题立意

试题的立意是指试题所包含的主要思想.[1]本例立意深刻,下面从基础知识、思想方法、核心素养三个方面进行分析.

(1)基础知识立意:命题者在遵循课程标准的前提下,以双曲线为载体,考查了高中数学的主干知识:双曲线方程、诱导公式、两直线夹角公式、三角形面积公式等,这有导向高中数学教学夯实基础、着力主干之意.

(2)思想方法立意:本题涉及函数与方程思想、化归转化与思想、数形结合思想等多种数学思想,对引导数学学习重视数学思想方法具有积极意义.

(3)核心素养立意:本题解答涉及较为复杂的运算和推理,充分考查数学运算素养和逻辑推理素养;解答(Ⅱ)问建构“两直线夹角”模型,考查数学抽象素养和数学建模素养;整个解答过程中建立了形与数间的联系,利用图形描述问题,借助几何直观理解问题,考查直观想象素养.

三、试题解法

从系统论来看,一个数学问题就是一个相对独立的系统,对系统的处理(解题)就是把系统中一个个零散的信息按照一定顺序串在一起形成一个有机整体.一题多解是解法研究的基本形式,体现的是信息组合的多样性和思维策略的灵活性[2].下面给出本题(Ⅱ)的解答.

分析:解答分为三步：求斜率kAP、kAQ，求三角形的各点坐标，求面积.

3.1 求斜率kAP、kAQ

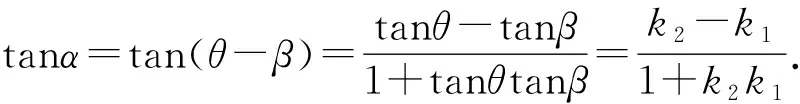
图1

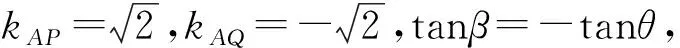
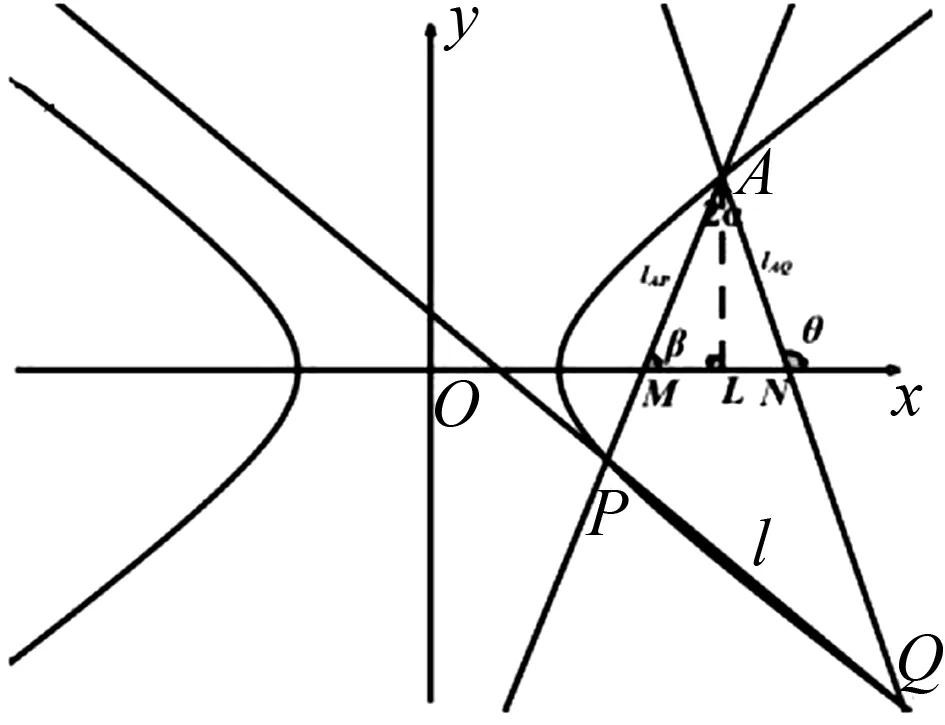
图2

3.2 求三角形的各点坐标

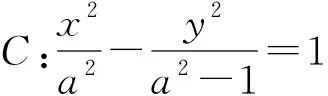
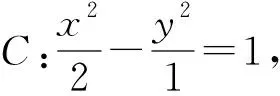
3.3 求△PAQ的面积

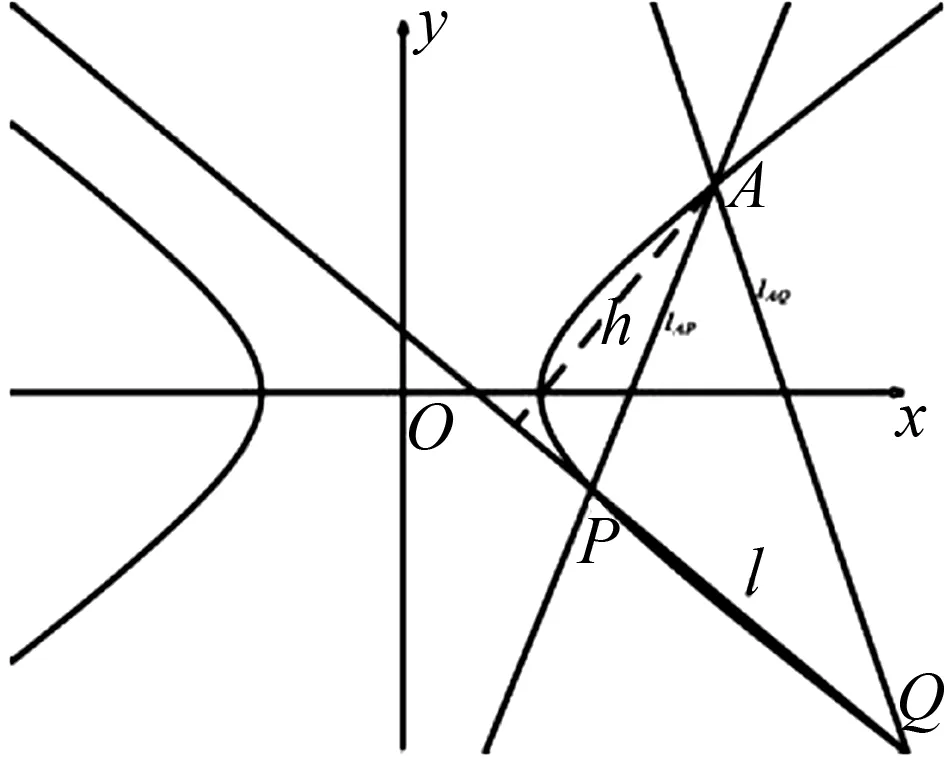
图3

法3：(分割三角形法)过三角形的某一个点作与x轴或y轴的平行线,将原三角形分割成两个一条边与坐标轴平行的三角形,分别求出面积后相加.

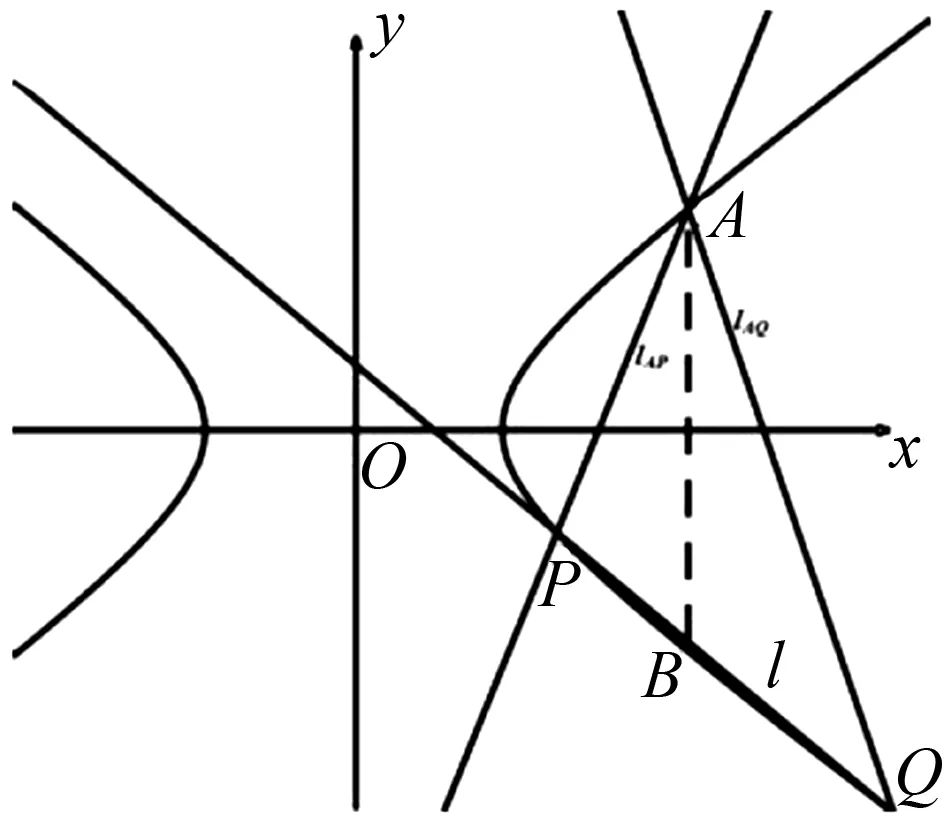
图4

注:由于篇幅问题,作y轴平行线的做法请读者自证.

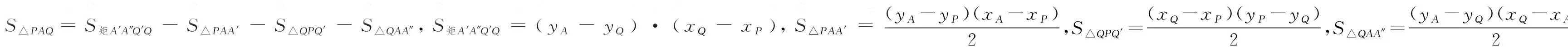
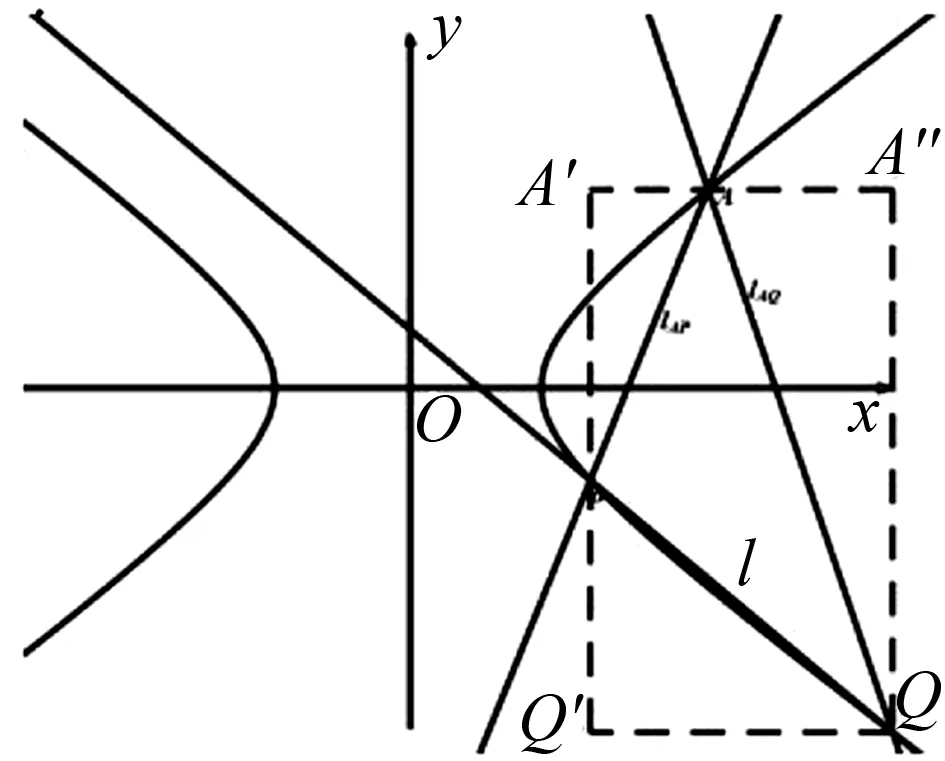
图5

注:由于篇幅问题,补足直角梯形求面积的做法请读者自证.

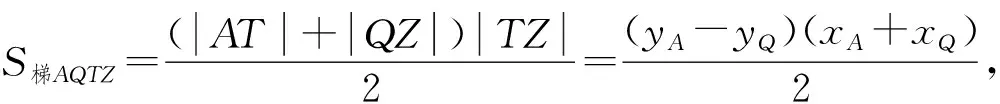
图6

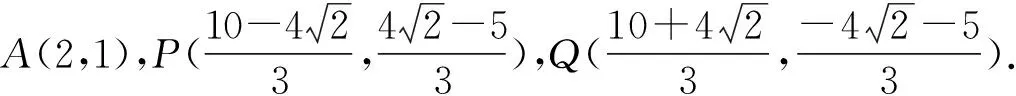
注:海伦公式计算量过大,在此不予展示,有兴趣请读者自证.

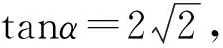
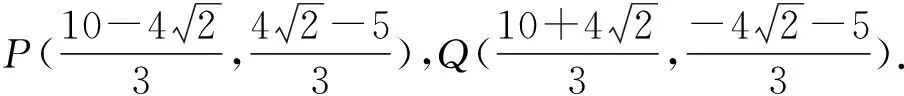
四、试题变式

变式是指相对于某种范式,不断变更问题情境或改变思维角度,使事物的非本质属性时隐时现,而事物的本质属性保持不变的变化方式.变式能有效控制题海战术,帮助学生形成良好的认知结构[2].

4.1 变试题求解目标

4.2 变试题求解目标及条件

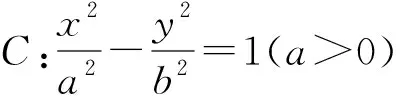
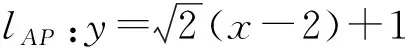
4.3 变试题背景及条件

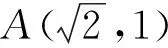
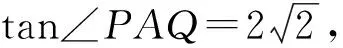
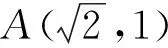
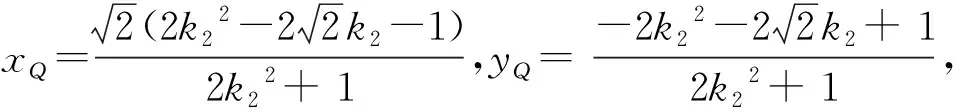
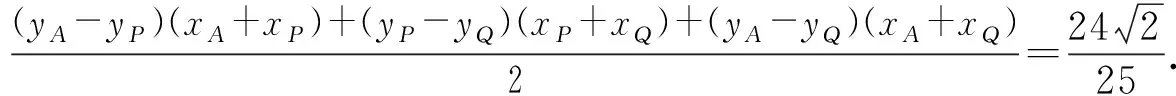
4.4 变试题背景、求解目标及条件

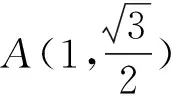
五、试题推广

数学推广是指根据问题结构或解决方法,将数学问题从一个较小的范围拓展到更大范围的研究过程.数学推广对培养问题意识、完善认知结构、体验研究历程、增强创新能力具有积极意义[3].