打破思维定式，落实核心素养

张亚光

(太和县马集镇中心小学 安徽阜阳 236638)

小学生掌握的数学知识较少，再加上逻辑思维能力比较薄弱，他们对新知的获取往往建立在模仿的基础之上。“数学是一门关于模式和秩序的学科”，在新知识的理解和运用上，小学生常因思维定式而犯错。要规避这种错误，引导学生向着思维定式的正方向发展，就要对思维定式有着更理性的认识。

一、思维定式的界定

认知心理学认为，由一定的心理活动所形成的准备状态对于问题的解决起到促进或妨碍的作用，这种状态叫作思维定式。可见，思维定式有其积极的一面，也有其消极的一面。作为教师，要运用恰当的教学手段引导学生朝着符合数学思维的方向发展，朝着思维定式积极的一面发展，使知识产生正迁移。

二、思维定式产生的原因分析

(一)正负迁移

问题1：简便运算25×125×32=

生1：25×125×32=25×125×(4×8)=(25×4)×(125×8)=…

生2：25×125×32=25×125×(4×8)=(25×4)+(125×8)=…

生1对乘法结合律非常熟悉，并且知道25和4常结合，125和8常结合，进而想到把32分成4×8，这是对乘法结合律的运用熟练到一定程度的结果，也是思维定式积极的一面。有了上述思维定式，便能很快地解答本题，此为知识技能的正迁移。

生2在运算时，看到两头乘，联想到乘法分配律。把乘法分配律负迁移到这里，是很多学生经常犯的错误。这主要是由于对乘法分配律的本质没有理解透，故而将乘法分配律和乘法结合律混淆。对于某些新知识，理解不透彻而产生知识运用上的干扰，此为知识技能的负迁移。

问题2: 脱式计算 35+65×40÷5

在四年级学习混合运算时，学生易犯先算加法的错误，如下面生3的做法。出错原因一方面是学生对“从左到右计算”和“先乘除，后加减”这两者的认知出现冲突，另一方面是对运算顺序理解不到位。

生3： 35+65×40÷5 生4： 35+65×40÷5

=100×40÷5 =35+260÷5

笔者认为更重要的原因是一年级就学习了加减法计算，学生已经习惯从左到右的计算顺序，在实际计算时，不知不觉又这样做，导致“从左到右”的计算法则在这里发生负迁移。

(二)经验主义

问题3：解方程5+3x=6

生5：5+3x=6，3x=1，x=3

生6：5+3x=6，3x=1，x≈0.33

生5在第二步系数化为1的时候，本该运用积除以一个因数，却因“习惯”了大数除以小数，结果用3除以1。之前的学习经验在这里产生了知识负迁移，导致出错。

生6在最后结果处取近似数，其原因是在低年级学除法时，没学分数，结果除不尽时就保留。基于这一经验，生4在学了分数后，没有形成用分数表示结果的习惯，结果还是取近似数。

可见，学生在旧知识较熟练，而新知识还不熟练时，会因思维定式产生知识负迁移。之前学习积累的经验反而成了学生解题的“绊脚石”。

问题4：爸爸今年31岁，比儿子的年龄2倍还多5岁，儿子今年多少岁？

对于这个问题，很多学生把算式错写成(31+5)÷2，其原因是在一年级时，习惯了见“多”就加，见“少”就减。学生不能从本质上理解爸爸和儿子年龄的数量关系，而是凭经验列式计算。教师往往利用线段图，或者结合方程解法让学生比较、辨析来纠正错误。在这个过程中，要让学生体验到经验不是什么时候都能用得上的，只有科学、正确地分析数量关系，才能找到正确做法。

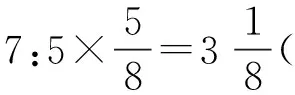
答：一个星期修不完。

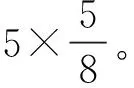
(三)审题不清

问题6：钟表上，从12点到1点，分针转了度。

本题常有学生错填“30”这个答案，原因是审题时没注意“分针”二字，思考时只想着12点到1点中间会有多少格、转了多少度等。

问题7：一个长方体长、宽、高都扩大2倍，体积会( )。

A.扩大4倍 B.扩大6倍 C.扩大8倍

五年级学生在做这个题目时，常错选B项，长、宽、高都扩大2倍，就是23，但是小学生对乘方计算还不熟练，把它当成了2×3来算。

三、打破思维定式的几点建议

(一)强化解题技能

魏书生老师说过，学习就是“发展、发展、再发展，生长、生长、再生长”。要强化学生正确的、积极的一面，以此来“对付”学生易错、易混的地方。这种教学思想，也可以用在纠正学生“思维定式负迁移”上面。数学是一门技能性学科，对于正确的技能，要达到熟练的程度才不会被“定势”干扰。学生在学习了新知识后，若没有做足够的题进行强化、形成技能，很容易产生知识的负迁移。如对于问题3，学生在学习了“因数=积÷另一个因数”这个知识点后，只有做题强化、定时复习，才会避免因“定式”而出错。只有对基本知识、基本技能的掌握达到一定熟练程度，才会产生思维定式的正迁移，避免思维定式的负迁移。在初学混合运算时，学生容易出现计算顺序错误，而这种错误在后期很少出现，是因为学生经过了大量的练习、纠错，熟练掌握了解题技能，理解了知识的本质。理解并掌握某一新知识，要有一个过程。在初学混合计算时，我们可以让学生先观察运算顺序再算。熟练掌握基本技能，是避免出现思维负迁移的一个有效措施。

(二)重视思维过程

课堂上，我们不仅要关注学生的学习结果，更要关注学生在学习中的思维过程。小学生的学习以形象具体思维为主，他们的学习往往不深入，需要我们老师不断鼓励、引导他们走向深入。小学生的数学语言很匮乏，我们常发现学生会做题，却说不出为什么这样做。这就要教师重视知识的产生过程，从本源抓起。如问题1，若对乘法分配律有透彻的认识，学生就不会写成25×4+125×8。

下面是笔者执教的一个教学片段。

师：你为什么把25×125×(4×8)这一步，写成25×4+125×8呢？

生8：因为我想25和4结合，125和8结合，就想到了乘法分配律，所以就这样做了。

师：乘法分配律用字母怎么表示呢？

生9：记不清了，好像式子两头乘法，中间加法。

生10：乘法分配律用字母表示是 (a+b)×c=a×c+b×c

师：这个式子左右两边各有什么特征呢？

生11：等式左边是两个数的和与一个数相乘的形式，右边是两个数分别与同一个数相乘，然后中间相加。

师：观察得很仔细，只有两个数的和或差与一个数相乘，才能变成“两头乘，中间加(或减)”的形式。而像25×125×(4×8)不可以变成25×4+125×8的形式，中间的加要改成乘才对。

作为一线教师，要站稳课堂，既要重视学习结果，又要重视学习过程。要在过程中，及时地反馈、评价，以此来促成好结果。

(三)培养学习习惯

要提高学生的思维品质，就要从培养学生的学习习惯抓起。教学时数学教师应该以严谨、认真的态度影响学生，小学生接受新知识的速度往往比较慢，帮学生打开思维、深入学习，比匆忙完成教学任务更重要。教育家杜威说过，“许多儿童由于缓慢，由于不能迅速作出回答而受到指责，其实，他们那时正在花费时间积聚力量以便有效处理他们面临的问题。在这种场合下，若不能留给他们时间和空间，那就是鼓励他们养成迅速的但却是仓促的浅薄的习惯”。我们教师要学会等一等，引导学生走向深入学习。因思维定式产生知识的负迁移，往往是数学学习过程中不细致、不严谨的结果。像问题5，细致的学生是能注意到“分针”二字的，犯错往往是因为不熟练、不细致，顾此失彼。数学是严谨的，我们要从平时抓起，从每一次数学思考抓起，培养良好的学习习惯。

(四)注重求异训练

A.第一根长 B.第二根长 C.无法确定

A.剪去的绳子长

B.剩下的绳子长

C.无法确定

这两题学生经常混淆，为此，笔者专门组织学生进行一次讨论。

生12：问题8中“绳子总长不知道”，因此选“无法确定”，那问题9中“绳子总长不知道”，为什么就可以确定谁长呢？

师：问题8中是两根绳子，问题9中是一根绳子。

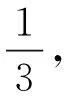
师：非常好，问题9中绳子长实际是一定的。不能一见到分数就以为它是分率，带单位的分数它就表示一个量。

俄国著名教育家乌申斯基说，“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切”。比较是学生学习数学的一个重要方法，要针对学生产生负迁移的地方，专门设计一些练习，让学生在比较后，进行充分的讨论、辨析，从而纠正错误的“定势”，形成知识的正迁移，最终实现正确的认知。小学生的思维常带有不深入、停留在表面等特点，因此我们要引导学生观察、比较、辨析。通过这些活动来提升学生的认识，加深学生对知识本质的理解，使学生思维走向深入。

四、结语

要避免思维定式产生负迁移，就要研究学生的“学”。只有充分了解学生，才能教好学生，才能使我们的教学目的明确、有效。我们只有把握学生的学习情况，引导他们朝着正确的方向发展，才能使学生避免因思维定式而产生知识负迁移。波兰数学教育家波利亚说过，“教师教什么，当然是重要的，但是学生心里想什么，想知道什么却是更重要的”。教师的教要建立在学生学的基础之上。教学中要认真对待学生所犯的每一个错误，利用好这一生成性资源。对于思维定式引发的错误，要让学生学会突破。只有更理性、更科学地处理学生因思维定式引发的错误，才能够因学定教，才能真正落实核心素养。