具有Bazykin功能反应的捕食者-食饵扩散模型的稳定性

赵明阳，孙福芹，刘朋燕

（天津职业技术师范大学理学院，天津 300222）

众所周知，生态系统能够反映物种与物种间、物种与自然环境间的相互作用，捕食者-食饵模型作为一类经典的生态系统模型，可以用来研究2个物种之间的动态相互作用，对于维护生态系统中物种的稳定性具有重要意义。在此基础上，众多学者深入分析捕食者-食饵相互作用的特征，构建了带有多种功能性反应函数的捕食者-食饵模型，包括Holling I-III功能反应、Holling-Tanner功能反应、Beddington-Deangelis功能反应以及Ratio-dependent功能反应等[1-4]。然而，在对捕食者-食饵模型的研究中，鲜有文献考察Bazykin功能反应函数。Bazykin功能反应可以描述捕食者饱和的不稳定力量与猎物竞争的稳定力量，这对于了解种群之间的作用更具实际意义。另外，现实世界中的猎物和捕食者总是处于运动状态，为准确模拟猎物和捕食者的动态特征，需要在模型中考虑种群的空间扩散[5-8]。因此，本文构建一个具有Bazykin功能反应的捕食者-食饵扩散模型，研究模型的有界性和平衡点的存在性，并对平衡点的局部稳定性、全局稳定性以及Turing不稳定性进行分析。

1 模型组成和初步结果

1.1 模型组成

考虑了一个具有Bazykin功能反应的捕食者-食饵扩散模型[9]如下

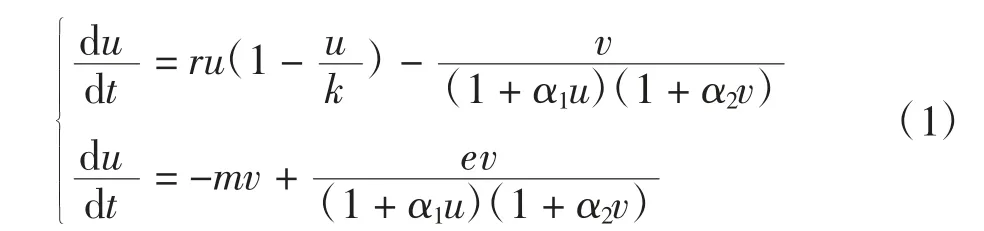
式中：u（t）为t时刻食饵种群的数量；v（t）为t时刻捕食者种群的数量；增长率r∈R+；环境承载力k∈R+；e为食饵到捕食者的转化率（0＜e＜1）；m为捕食者的恒定自然死亡率。

Bazykin型功能性反应函数为f（u，v）=1/（1+α1u）·（1+α2v）。其中，α1和α2为2个正常数，且α1＞α2，用来描述捕食者饱和的破坏稳定力和争夺猎物的稳定力。

在现实世界中，猎物和捕食者始终处于运动状态，该现象可以利用自扩散来模拟。假设所考虑的2个种群总是在运动，每一个种群都遵循1条路径，路径的长度用x表示。考虑以上假设，模型（1）可以写为如下形式

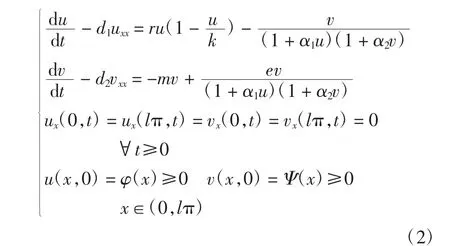
式中：d1、d2分别为食饵和捕食者的扩散率；x为捕食者或食饵在时刻t所在的位置；lπ为所在区域的范围。Neuman边界条件表示食饵和捕食者的移动距离为0～lπ。以上所有参数均为非负[10]。

1.2 平衡点的存在性

通过求解du/dt=0，dv/dt=0可以得到模型（2）的平衡点，显然，模型（2）有平衡点E0（0，0），E1（k，0）以及E2（u*，v*）。u*、v*可根据方程组（3）求解得出

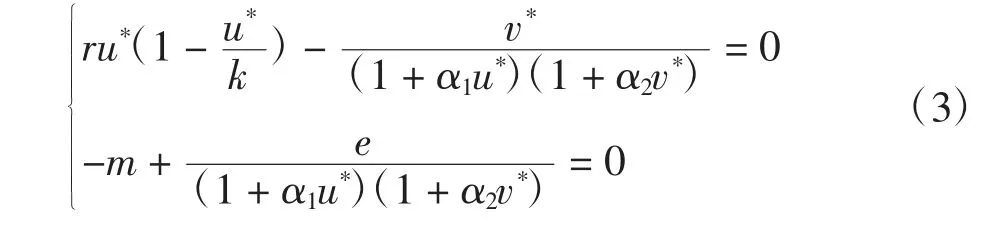
1.3 有界性

下面给出问题（2）解的有界性结论。

定理1当u0（x）≥0，v0（x）≥0且不恒等于0时，系统（2）有唯一解（u（x），v（x））；当t＞0，x∈（0，lπ）时，0＜u（x，t）＜u*（t）且0＜v（x，t）＜v*（t）。其中，（u*（t），v*（t））为常微分方程（4）的唯一解

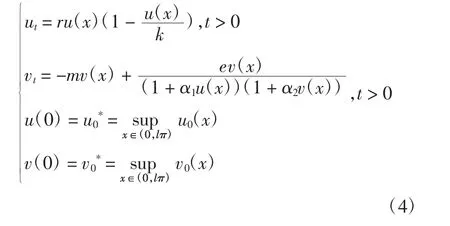
进一步可以得到

证明令

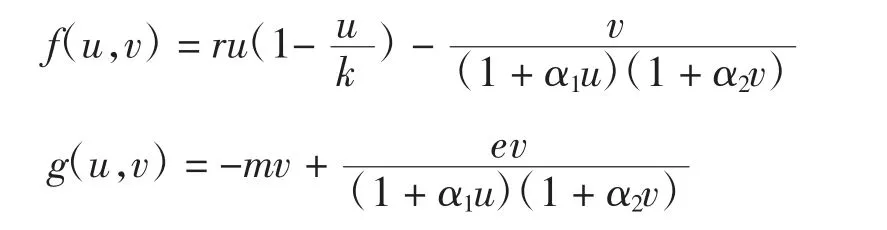
f和g的偏导数为

因此，f和g为Lipschitz函数，故存在正数c1、c2对于u1、u2、v1、v2有

令（u2（x，t），v2（x，t））=（u*（t），v*（t）），满足方程

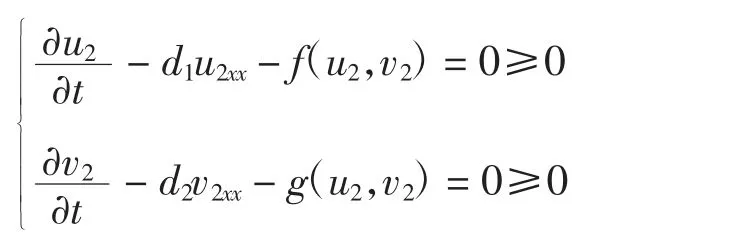
令u1（x，t），v1（x，t）=（0，0）满足方程

其中，0≤u0（x）≤u0*，0≤v0（x）≤v0*，则（u1（x，t），v1（x，t）），（u2（x，t），v2（x，t））分别为系统（2）的上解和下解。强极大值原理表明，当t＞0且x∈（0，lπ）时，u（x，t）＞0，v（x，t）＞0。至此，完成了第一部分的证明。

u（x，t）≤u*（t），v（x，t）≤v*（t），u*（t）为方程ut=ru（x）（1-u（x）/k）的唯一解，且u（0）=u0*＞0。容易证明当t→+∞时，u*（t）→k。所以，对于∀ε＞0，∃T0＞0使得u（x，t）≤k+ε。从而得到，当t＞T0，x∈（0，lπ）时，sup u（x，t）=k。

令

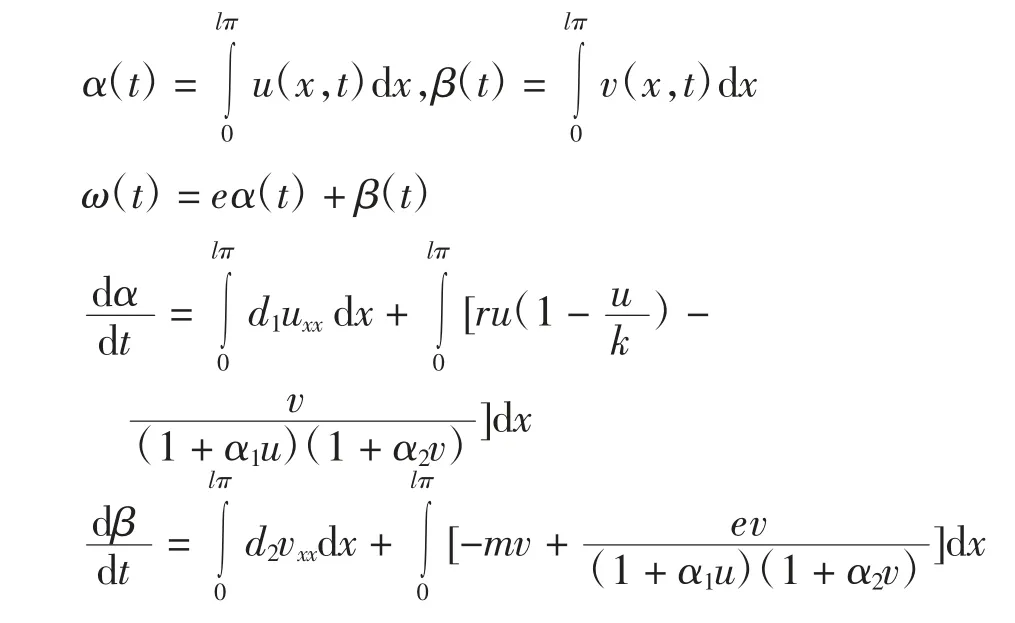
根据Neumann边界条件

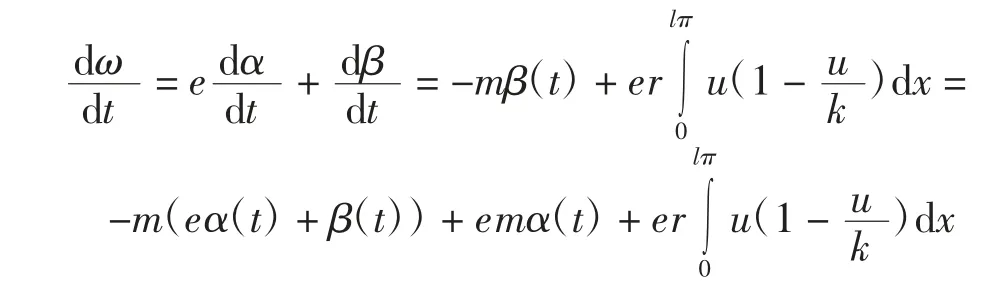
可以得到

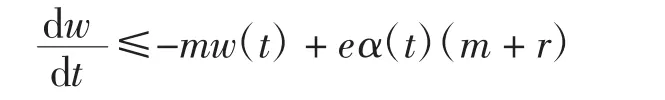
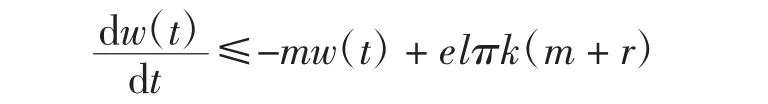
得到

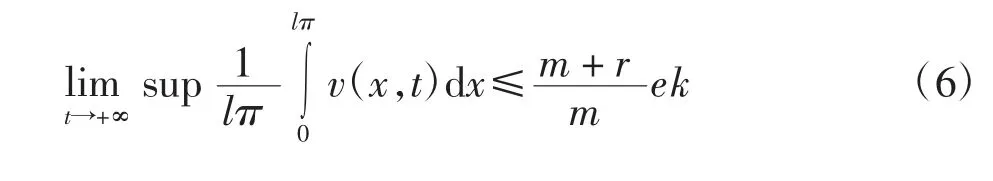
2 稳定性分析

系统（2）在任意点（u，v）处的Jacobian矩阵为J=（mij）∈R2×2，

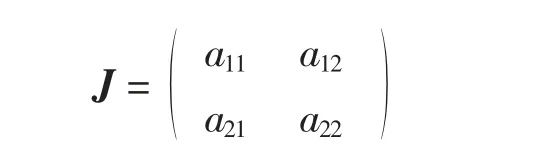
D=diag（d1+d2）及其对应带有Neumann边界条件的实值Sobolev空间可定义为

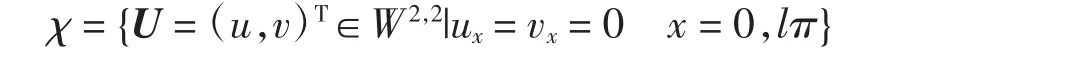
其内积为

相关χ的Hilbertian范数记为‖·‖2.2，相关的特征值问题为

其中，kn=（n/l）2和cos（nx/l），n=1，2，3…分别为式（7）的特征值和特征函数。

2.1 E1（k，0）的局部稳定性

平衡点E1（k，0）的线性化系统为Ut=DΔU+J（k，0）·U，矩阵-（n/l）2D+J（k，0）的特征值为

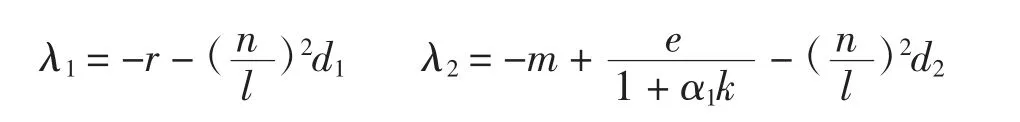
定理2当R1=m+e/（1+α1k）＜0时，系统（2）在平衡点E1（k，0）处是局部渐近稳定的。

2.2 E1（k，0）的全局稳定性

分别定义系统（2）的上常数解和下解（u1，v1）=（k+ε，M）和（u2，v2）=（ε，0）。其中，ε、M为正常数且ε足够小；定义（）和（），m=1，2，3…为耦合抛物型方程[11]

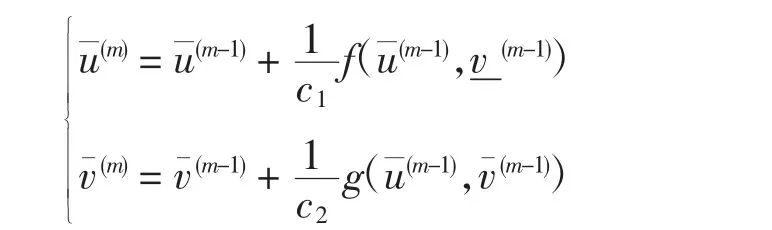
和

根据Pao[11]的定理2.1

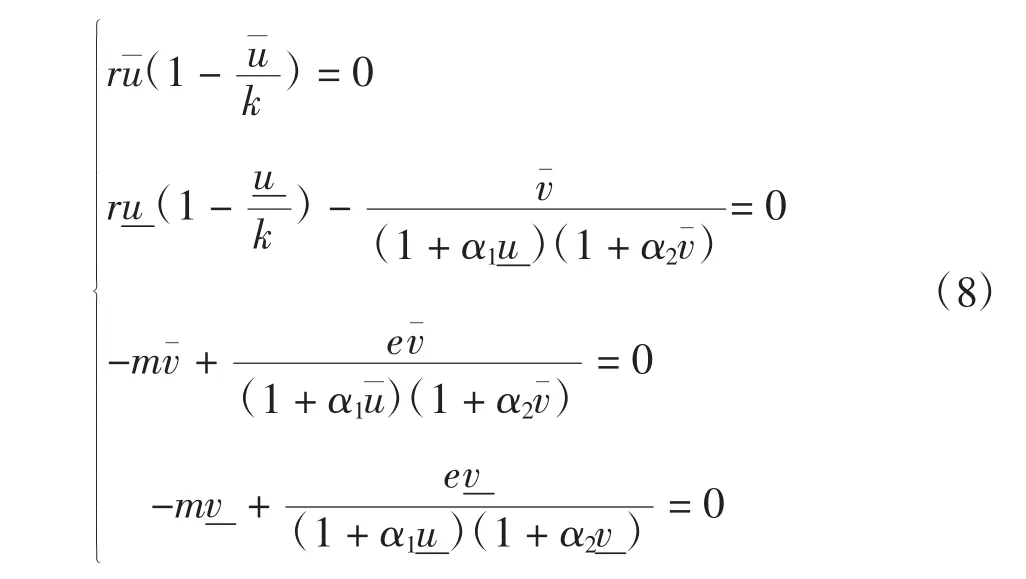
运用比较定理证明方程u（x，t）≤γ（x，t），（x，t）∈[0，lπ]×[0，+∞]，通过下面的抛物方程

得到t→+∞时，γ（x，t）→k，在[0，lπ]×[t0，+∞]中，存在t0＞0时，u（x，t）≤k+ε，这意味着平衡点E1全局吸引，并且定理2证明了在满足特定条件的情况下，E1局部渐近稳定，因此能够得到E1全局稳定。

2.3 E2（u*，v*）的Turing不稳定性

系统（2）在正平衡点（u*，v*）处的雅可比矩阵为

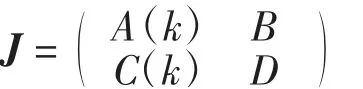
系统（2）写成如下形式

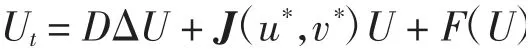
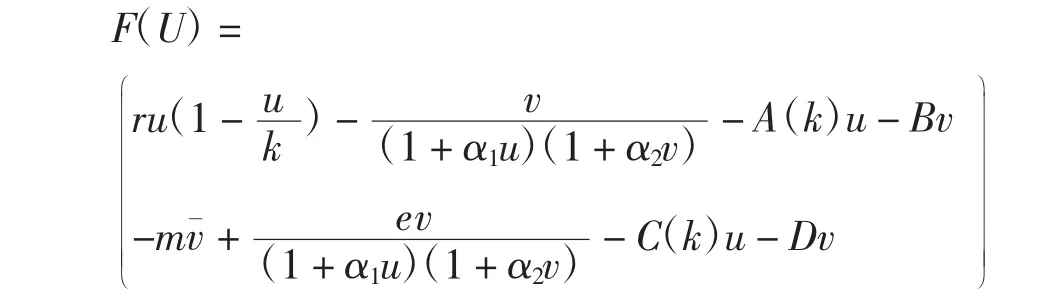
F（U）是围绕平衡点E2（u*，v*）的非线性函数。

系统（2）在E2（u*，v*）处的线性化系统为：Ut=DΔU+J（u*，v*）U-（n/l）2D+J（u*，v*）。其中，-（n/l）2D+J（u*，v*）的矩阵为

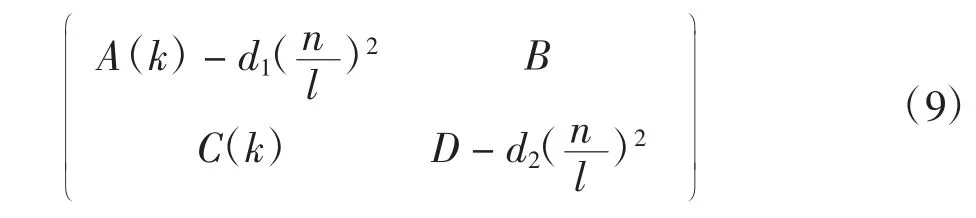
矩阵（9）的特征值为方程（10）的解

Turing不稳定性的存在需要满足以下2个方面[12]：

（i）当没有扩散时，平衡点是线性稳定的，D0（k）＞0；

（ii）在扩散存在时，平衡点变得不稳定，Dn（k）＜0。

由于

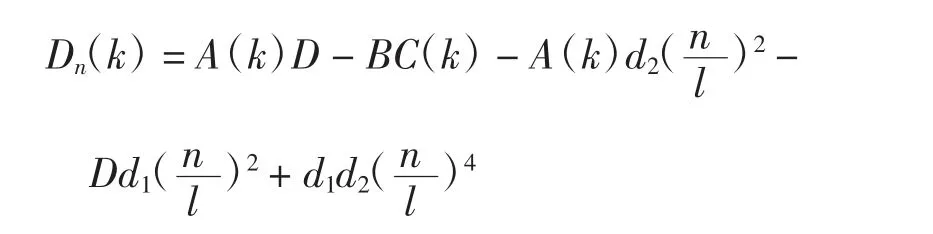
所以

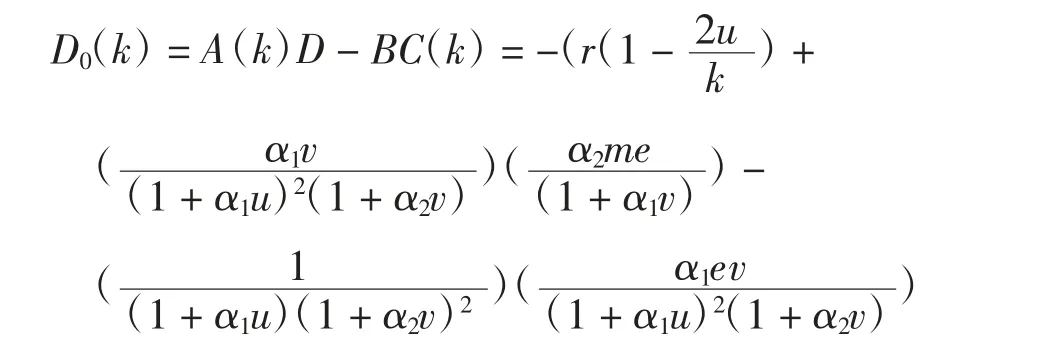
显然D0（k）＜0，由此可以得到Turing不稳定性的不存在性。

3 结语

本文考虑了齐次Neumann边界条件下，具有Bazykin功能反应的捕食者-食饵扩散模型。首先，证明了模型的有界性和平衡点的存在性，得到模型的3个平衡点E0、E1、E2；其次，证明了在没有E2的情况下，E1的局部稳定性以及全局稳定性；最后，通过对平衡点E2（u*，v*）的特征方程进行分析，证明Turing不稳定性的不存在性。通过分析具有Bazykin功能反应函数的捕食者-食饵扩散模型的稳定性，有助于未来对具有Bazykin功能反应函数模型的分支问题进行更深一步的研究。