精密机床直线进给轴位姿误差建模方法研究

孙光明，张大卫，孙铭泽，胡高峰，李志军

（1.天津大学机构理论与装备设计教育部重点实验室，天津 300072；2.天津城建大学控制与机械工程学院，天津 300384；3.天津理工大学机械工程学院，天津 300082；4.天津职业技术师范大学机械工程学院，天津 300222；5.天津大学内燃机燃烧学国家重点实验室，天津 300072）

精密机床是制造业的核心设备，直线进给轴是机床的重要部件，其位姿误差直接影响机床的末端精度。直线进给轴存在6项运动误差，其中运动方向的位置偏差与2项直线度误差称为位置误差，3项转角误差称为姿态误差，位置误差与姿态误差合成位姿误差。影响直线轴位姿误差的因素主要包括导轨几何误

差[1-2]、弹性变形[3]、热误差[4]和伺服参数[5]等，其中装配后的导轨几何误差是影响直线轴位姿误差的重要因素。直线轴位姿误差建模是建立导轨几何误差与位姿误差之间的数学模型。目的是在装配过程中，通过测量几何误差实现对位姿误差的预测；根据给定的位姿误差要求，通过精度设计的方法，对几何误差优化分配。位姿误差建模是精度预测和精度设计的关键环节，本文从静力平衡建模法、等效刚度建模法、有限元建模法等方面，探讨现有直线轴位姿误差建模方法的特点及尚需解决的问题。

1 静力平衡建模法

静力平衡建模法是根据直线运动轴的结构特征，分析其受力状态，根据力学知识将系统中的力和力偶矩按照力的平移法则，将它们向坐标系的原点简化为1个合力矢和1个合力偶矩，再根据力和力偶矩的方向，获得运动轴在各个方向上的平衡方程。静力平衡建模法的基本数学模型为

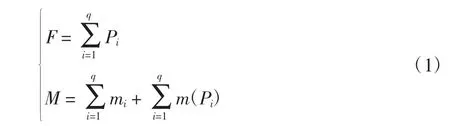
式中：F为合力矢；M为合力偶矩；q为运动轴所受力的数量；Pi为运动轴所受第i个分力的大小；p为运动轴所受力偶矩数量；mi为第i个分力偶矩的大小。

Shimizu[6-7]利用赫兹接触理论分析了滚动导轨中滚动体的受力状态和载荷分布，在此基础上，运用力平衡方程和力矩平衡方程，研究了滚动导轨支撑下直线运动系统的载荷分布和刚性特征。周传宏等[8]以精密滚动直线导轨副工作台为研究对象，运用力学和运动学知识推导出在任意力和力偶矩作用下，工作台中滚动直线导轨副负载以及工作台上任意点的位移。较早期使用静力平衡建模法研究了四滑块双导轨和六滑块双导轨结构的直线运动轴的负载分布，结合变形协调方程获得了各个滑块的受力和变形状态，并得到了工作台的转角误差。四滑块导轨副负载与变形协调如图1所示。

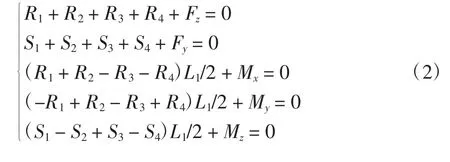
静力平衡方程为式中：R1至R4分别为工作台在z方向所受作用力；S1至S4分别为工作台在y方向所受作用力；Fy和Fz分别为作用在工作台中心沿y和z方向的力；Mx、My和Mz分别为作用在工作台中心沿x、y和z方向的力矩；L1为滑块沿x方向的距离，L2为两导轨之间的距离。

变形协调方程为

工作台的位姿误差

式中：δ1至δ4分别为四滑块在z方向的弹性变形；δ1'至δ4'分别为四滑块在y方向的弹性变形；φx、φy、φz分别为工作台绕坐标系中x轴、y轴、z轴的转角误差。

应强[9]、范静锋[10]使用静力平衡建模法研究了滚动直线导轨静刚度、导轨副载荷特性和结构特点。Wu等[11]在研究直线轴位姿误差的过程中考虑了导轨滑块的刚度，运用静力平衡建模法研究四滑块双导轨系统的受力状态，并获得了工作台的运动姿态。刘曙光[12]运用静力平衡建模法计算了四滑块双导轨系统的受力状态，研究了滚柱直线导轨力学性能，获得了工作台的姿态误差。静力平衡建模法不仅可以用于误差建模，还可以用于分析滑块磨损和载荷分布研究。Fan等[13]利用静力平衡方程求解滑块和导轨之间的接触面上产生的反作用力，在此基础上建立了机床直线轴的精度损失模型，根据滑轨的磨损量预测工作台长期运行后的定位误差。Sun等[14-15]结合材料滞弹性，运用静力平衡建模法建立直线进给轴的重复定位误差模型，研究装配误差和结构件刚度对重复定位误差的作用机理。

除了滚动导轨支撑的直线轴之外，静力平衡建模法在非滚动导轨（静压导轨、气浮导轨）支撑的直线运动轴误差建模方面也有着广泛的应用。Onat等[16]研究了空气静压导轨几何误差与位姿误差之间的关系，建立了位姿误差的数学模型，建模过程中使用轴承位置和刚度、导轨几何误差和静态平衡来生成矩阵形式的模型。Xue等[17]在研究静压导轨误差均化效应的过程中，建立了四垫块运动系统的静力平衡方程，获得了系统的位姿误差和转角误差，静压导轨受力平衡分析如图2所示。

图2 静压导轨受力平衡分析

Wang等[18]以工作台运动平衡方程和液膜雷诺方程为基础，考虑了流体的可压缩性和挤压油膜效应，提出了流体静压导轨的位姿误差建模方法，获得了四垫闭式静压导轨的直线度误差和转角误差。Qi等[19]应用流体静力平衡建模法，建立了单垫和双垫静压导轨的误差均化模型，提出了一种考虑导轨三维轮廓误差的静压导轨误差均化效果的评估方法。Zha等[20-21]为了研究直线度误差的不同变化趋势，分析了考虑外部载荷的四垫开式静压导轨的静态平衡条件，建立了误差均化的数学模型。

静力平衡法具有计算简便、应用范围广的优点，但这种方法仅能适用于理想状态下直线轴位姿误差的建模，而实际装配后的直线进给轴不可避免地存在装配误差，因此静力平衡建模法难以进行精确建模。

2 等效刚度建模法

等效刚度建模法是在赫兹接触理论和静力平衡建模法的基础上发展而来的[22-24]，该方法在建模过程中考虑导轨滑块的等效刚度，并能够建立多种类型导轨误差的传递模型。Shamoto等[25-27]提出了传递函数模型，该模型将滑块所受合力的幅值与导轨几何误差的幅值之比定义为传递函数K（ω），且K（0）为导轨滑块的等效刚度，根据静力平衡方程分析工作台的受力状态，获得工作台的位姿误差。传递函数的表达式为

式中：fe（ω）为工作台所受合力的幅值；e（ω）为导轨几何误差幅值。

Khim等[28-29]运用传递函数理论，对滚动导轨支撑的直线轴误差建模，建模过程中根据赫兹接触理论推导了在导轨几何误差影响下滑块的受力情况，将滑块所受合力与导轨几何误差的幅值之比等效为导轨滑块的刚度K（0），并以此为桥梁，根据静力平衡方程分析工作台的受力状态，获得了工作台的位姿误差，以传递函数为等效刚度的建模方法如图3所示。

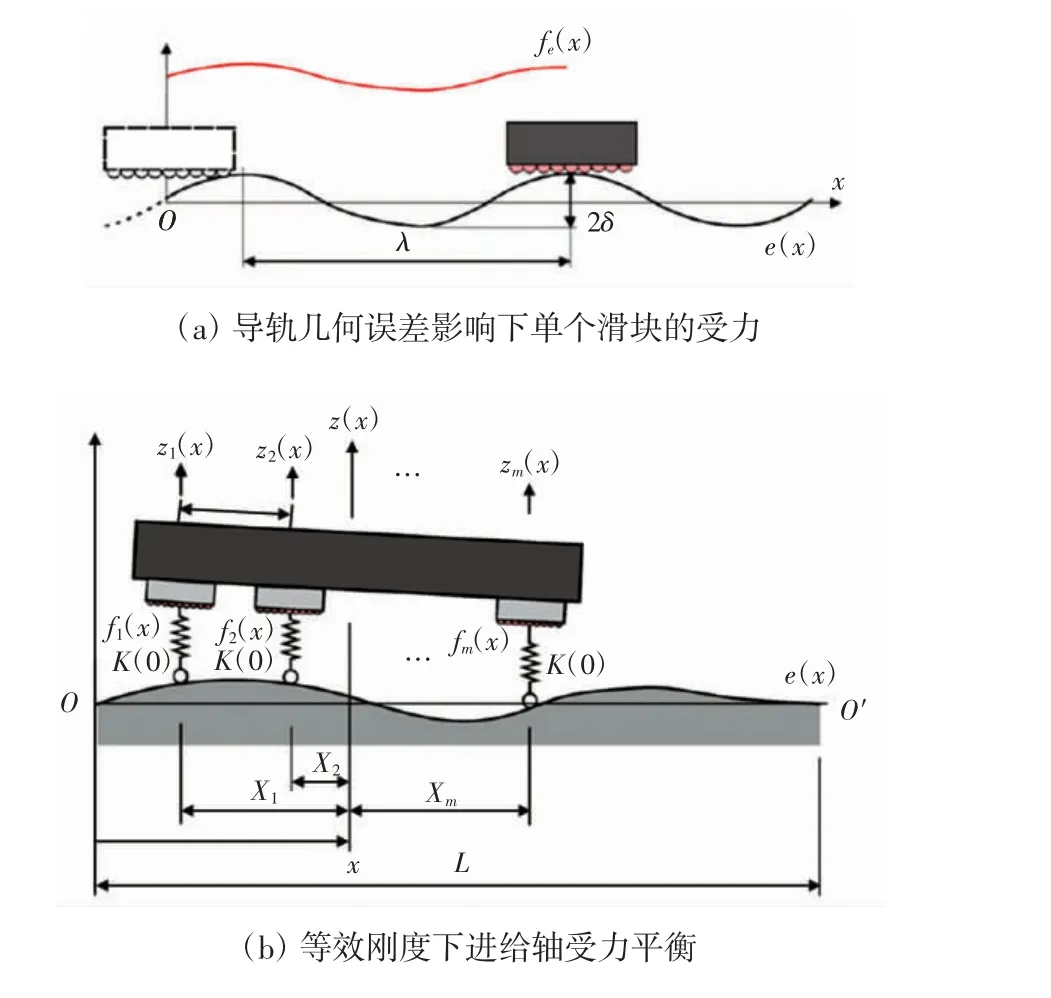
图3 以传递函数为等效刚度的建模方法

以传递函数为等效刚度的静力平衡方程为

式中：fei（x）为第i个滑块对工作台的作用力；Zi（x）为第i个滑块组在z方向的位移；Xi为相邻2个滚动体组之间的中心距离。

在此基础上，Hwang等[30]运用该误差传递函数理论，根据导轨轮廓的空气静压轴承的力平衡，预测XY型工作台二维位姿误差。随后，Khim等[31]基于等效刚度建模法，提出了一种工作台五自由度位姿误差的计算方法。研究建立了导轨的实际几何误差和工作台位姿误差之间的关系，实现了气浮导轨支撑的直线轴五项位姿误差的预测，将工作台位姿误差模型扩展至三维（3D）范围。

Kim等[32]运用等效刚度建模方法，采用双弹簧系统，考虑到导轨平行度和垫间距误差引起的反作用力力矩的影响，建立了考虑导轨平行度的误差模型，进一步提高预测精度。在使用等效刚度建模法建模过程中，需用傅里叶变换将实际导轨轮廓误差转换为周期函数。对于大多环境，导轨表面曲线是随机的，为了建立导轨轮廓误差和位姿误差之间更加精确的数学模型，Tang等[33]提出了一种基于测量导轨表面和拟合曲线的直线度和角度误差的系统计算方法，导轨随机误差作用下工作台位姿误差如图4所示。

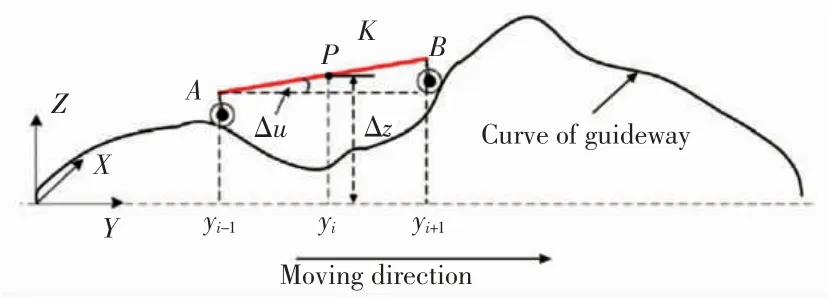
图4 导轨随机误差作用下工作台位姿误差

根据导轨误差测量结果选择合适的特征函数进行曲线拟合，进而计算位姿误差，该方法与传统方法相比，在曲线拟合和误差计算方面更为精确，可以通过同样的程序应用于其他类似的环境。此外，Xue等[17]在静压导轨误差均化建模过程中，将每个垫块油膜等效为支撑刚度，研究直线轴的位姿误差。

等效刚度建模法通用性强，能够适用于静压导轨、气浮导轨以及滚动导轨，建模时需要导轨导向面的轮廓误差，它在一定程度上决定了模型的预测精度。

3 有限元建模法

静力平衡建模法和等效刚度建模法是在滑块滚动体为弹性体、其他部件为刚体的假设下提出的模型。随着计算机仿真技术的发展，有限元建模法的应用越来越广泛，该方法可将参与计算的零件作为弹性体[34-35]。

在建立有限元模型的过程中，元件之间的接触特性以及滚动体的模拟是难点。Chlebus等[36]采用有限元建模法计算了滑动导轨接触层的刚度，将2个元件接头的接触层设置为一种的“第三体”，并根据接触特性赋予材料属性，该方法考虑了接触层的非线性特性。Wu等[37]在研究滚动导轨动态特性的过程中，为了模拟滚动界面的接触特性，在每个球体的上、下侧分别采用了零厚度的三维膜接触单元建模。Ohta等[38]研究了考虑滑块和导轨柔性的预加载线性导轨型滚珠轴承的垂直刚度，建立了导轨滑块的有限元模型，在滚动体的接触点施加了等效载荷，计算了滑块的变形。Hung等[39]在赫兹接触理论分析的基础上，采用弹簧单元模拟导轨滑块的滚动体刚度，建立了立柱运动部件的有限元模型，分析了机床的动态特性。Shi等[40]在对机床进行有限元建模时提出，导轨由梁单元表示，滑块由面单元表示，滑块安装面采用Glue命令相连，同时与滑动点Node用Mean命令相连，而滑动点与导轨上对应的Node节点重合，采用Bushing刚度单元相连，Bushing单元可以设定六维的静刚度。

目前，通用的有限元建模法为Majda[41]提出的一种直线导轨几何误差对工作台位姿误差影响的分析方法，该方法考虑到导轨几何误差的非线性特性，将滚动体等效为弹簧单元，通过改变弹簧单元的长度来模拟导轨几何误差，建立了双导轨四滑块系统的有限元模型，并研究了多种导轨误差状态下工作台的转角误差。在此基础上，郭龙真[42]使用有限元方法建立了机床直线轴导轨滑块系统的刚弹耦合模型，将导轨滑块的滚动体简化为等刚度的弹簧，通过修改弹簧的长度来模拟导轨的几何误差，研究了工作台在不同导轨误差状态下的位姿误差和转角误差，并进一步研究了直线轴的误差均化机理和低应力装配技术。直线轴有限元模型如图5所示。

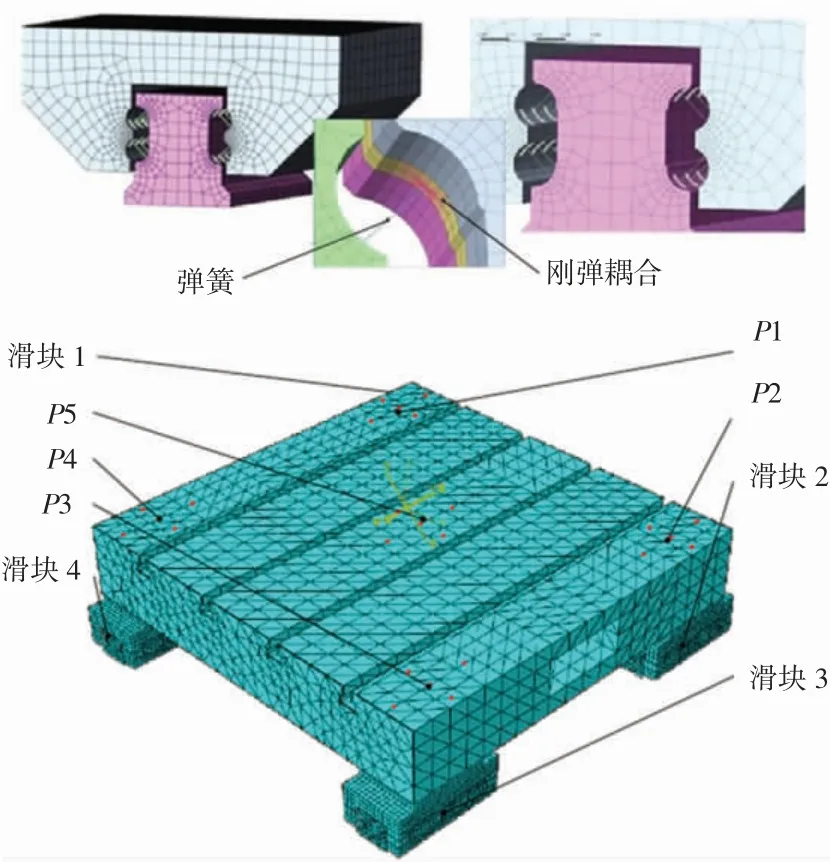
图5 直线轴有限元模型

有限元建模法的优点是所有零部件均作为弹性体参与计算，计算精度更高，缺点是建模过程繁琐，时间较长，模型通用性差。

除静力平衡建模法、等效刚度建模法和有限元建模法外，还有学者提出了各自的建模方法。何改云等[43]基于齐次坐标变换和最小余能原理定量分析了工作台的位姿误差，研究了直线滚动导轨平行度误差对机床工作台位姿误差的影响。Ekinci等[44]提出了一种基于误差分类的机床误差分析方法，研究了机床直线轴转角误差和直线度误差之间的关系。类似地，Wahid等[45]使用积分法建立导轨直线度误差和工作台位姿误差之间的映射模型。Ma等[46]基于激光跟踪仪，研究了零件制造误差和变形对直线轴位姿误差的影响。He等[47]提出了分层误差建模法，把直线轴的误差分为基面层误差、导轨层误差、滑块层误差、工作台误差，使用静力平衡建模法和等效刚度建模法分层建模，取得了较好的效果。

4 结论

本文综述了国内外机床直线进给轴位姿误差建模方法的进展和成果，分析了现有方法的特点。着眼于精密、超精密加工，当前的机床直线轴位姿误差的建模方法仍然存在一些不足，需要从以下几个方面深入研究：

（1）现有的建模方法着重于预测机床定位的准确度，然而体现机床定位稳定性的重复定位误差已经成为影响机床定位性能的关键因素，其建模方法还有待进一步研究。

（2）机床的动态误差已经成为影响机床定位精度的重要因素，目前的建模方法从不同角度衡量导轨几何误差对位姿误差的影响程度，属于静态建模，建立准确的动态误差模型，需要进一步研究。

（3）降低装配后的导轨几何误差是提高机床精度的重要途径，但目前位姿误差建模的目的多用于精度预测，基于控制导轨几何误差的精度设计方法是未来研究的重要方向。