基于遗传算法的含真空锁状态约束的集束型设备智能调度

黄国新，林文文，章天吉

（1.奥克斯空调股份有限公司，浙江 宁波 315100；2.奥克斯集团有限公司，浙江 宁波 315100；3.宁波大学 机械工程与力学学院，浙江 宁波 315211）

半导体设备作为半导体芯片加工厂的微小单元，承担了芯片制造过程中的多个重要环节。半导体设备产能的高低直接影响芯片加工厂的效益，而高效稳定的调度系统是保证最优产能的前提。由于设备内的加工存在诸多步骤和约束，从而导致了设备调度系统的设计十分复杂。与此同时，由于设备内对晶圆的调度要求实时进行，因此对系统的计算速度有着较高要求。

在众多半导体设备中，集束型设备（Cluster Tool）是具有代表性的一类设备。该类设备由加工模块（Processing Module，PM）、校准模块（Aligner，AL）、冷却模块（Cool，CL）、真空锁（load lock，LL）和搬运模块（Transfer Module，TM）构成，晶圆经过设备内各个模块以完成指定工艺。

目前为止，有关晶圆生产的单臂束集束型设备的调度研究已有不少工作，研究方法上主要有数学规划法、事件图、Petri网和分支定界法[1]。文献[2，3]中借助时间图工具，对单臂和双臂的集束型设备建立了考虑搬运机械手资源约束及处理腔资源约束时的调度基础周期（Fundamental Period，FP）模型，在此基础上分析了FP对设备产能的影响，但其仅仅考虑了单种晶圆的No-wait调度问题。文献[4]采用事件图描述加工模块和机械手的活动，提出了隐枚举思想的搜索算法。文献[5]提出了一种构造晶圆周期序列的策略和实现该策略的构造算法。Chauvet等[6]提出了基于时间窗的含加工时间约束的调度算法，但未考虑晶圆的搬运时间。周炳海等[7]研究了考虑晶圆多次重入的集束型设备调度，并提出了一种启发式算法使系统总完工时间最小化。刘明祥[8]等对带有驻留约束且具有多种晶圆类型的集束型设备群的调度问题进行了研究，在引入时间约束集概念的基础上建立了调度模型，同时，提出了一种逐级回溯的调度方法。然而，这些研究都忽略了真空锁状态转换对于内外机器手搬运晶圆的影响。

本研究的真空锁状态转换对机械手搬运晶圆的影响，真空锁存在大气状态和真空状态。真空锁可以在大气状态与真空状态间转换，外部的机器手需要真空锁在大气状态下，才能将晶圆搬入或搬出真空锁，设备内部的机器手需要真空锁在真空状态下，才能将晶圆搬入或搬出真空锁，这极大地影响了机械手搬运晶圆的效率，如何尽可能地避免或减少机械手在真空锁处等待真空锁状态转换的时间成为难题，针对这一问题建立了带真空锁状态转换约束的数学模型，并且采用遗传算法来解决该调度问题，又针对传统遗传算法容易陷入局部最优，遗传参数难以确定的问题，采用了自适应改变交叉和变异概率的算子调整概率值，从而避免早熟问题的出现，并解决了遗传参数难以确定的问题。

1 问题描述

本研究的集束型设备由真空锁模块（load lock，LL）、校准模块（Aligner，AL）机械手搬运模块（robot module，RM）、若干加工模块（process module，PM）以及冷却模块（Cool，CL）构成，每个PM有一个槽位，可放置一片晶圆加工。晶圆在集束型设备的生产过程如图1所示。

图1 集束型设备生产过程

生产过程描述如下：

LP为晶圆盒，用于存放晶圆。首先，晶圆加工前须放置在AL处做校准，晶圆完成校准后才能被取走。接着，取走的晶圆从真空锁LLA进入系统，按事先设定的顺序依次经过一个或多个PM加工后，返回到真空锁LLB中进行冷却。最后，冷却完成的晶圆直接从真空锁中取出。

为了有效地描述集束型设备的调度问题，做出如下基本假设和定义：（1）研究对象是单集束型设备。（2）晶圆搬运模块采用单臂机械手，每个机械手每次只能搬运一片晶圆。（3）每个加工模块每次只能放置一片晶圆进行加工。（4）晶圆的加工路线相同。（5）晶圆加工前须放置在AL处做校准，晶圆完成校准后才能被取走。（6）真空锁LLA与LLB可在大气状态与真空状态间转换，当LLA或LLB状态转换为大气状态，机械手TM1才能将晶圆送入或取走，当LLA或LLB状态转换为真空状态，机械手TM2才能将晶圆送入或取走。LLA与LLB从状态的转换需要时间。（7）晶圆的加工时间远大于机械手的操作时间，但并不忽略机械手的操作时间[7]。（8）晶圆加工完成后需放在真空锁中进行冷却，冷却完后才能被取走。（9）晶圆的加工路径为：

LLA→PM3/PM4→PM1/PM2/PM5/PM6→LLB

为清晰描述调度问题，作以下符号及变量定义：

集合：

I表示待加工晶圆集；

J表示晶圆的工序集；

Gj表示工序j的并行机器数目，Gj=1表示工序i只有一个加工模块可以使用；

常数：

Pij表示第i片晶圆在工序j的机器上的加工时间；

Tget表示机械手完成装载活动所需要的时间，为定常数；

Tput表示机械手完成卸载活动所需要的时间，为定常数；

T1表示真空锁从真空状态转换为大气状态所需要的时间，为定常数；

T2表示真空锁从大气状态转换为真空状态所需要的时间，为定常数；

Tij噪r表示第i片晶圆从工序j的机器噪上运输到下一工序的机器r上的时间；

变量：

Xij噪表示第i片晶圆在工序j的加工模块的机器噪上进行加工时，Xij噪=1，否则Xij噪=0；

LLm表示真空锁m的状态，当真空锁处于大气状态时，LLm=0，否则LLm=1；

Sij噪表示第i片晶圆在工序j的机器噪上的开始时间；

Cij噪表示第i片晶圆在工序j的机器噪上的离开时间；

tij噪表示第i片晶圆运输到下一工序的机器噪时，因真空锁状态切换等待的时间；

调度目标是最小化晶圆加工的总完工时间，因此，目标函数为：

在真空锁处等待的时间：

加工模块同时只能加工一片晶圆：

晶圆需加工完成后才可离开加工模块：

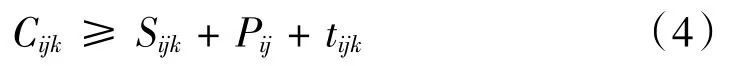
搬运每次仅搬运1片晶圆，且装卸时间相同：

晶圆一个阶段只在一台设备上加工：

晶圆进入首个加工模块的时间须满足：

2 遗传算法设计

遗传算法（Genetic Algorithm，GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法包括了编码、交叉、变异、选择等重要操作步骤。针对晶圆生产调度问题的多约束、多维度求解特性，对遗传算法进行适应性改进。

2.1 染色体编码与解码

半导体晶圆调度需要解决工序与生产设备的对应问题，因此，在染色体编码中需包含这方面的信息。本研究提出了一种染色体的编码方式，假设有3个待加工晶圆，晶圆1、晶圆2和晶圆3均具有3道工序，第一道工序和第二道工序可选生产设备有2台，第三道工序可选生产设备有3台。

染色体的编码如图2所示，数字1、2、3代表的是晶圆在不同工序选择的机器编号，由于一个晶圆有3道工序，因此前3个数字1、2、2表示晶圆1在这三道工序上分别选择第一台机器、第二台机器和第二台机器，中间3个数字2、1、3表示晶圆2在这三道工序上分别选择第二台机器、第一台机器和第三台机器，最后3个数字1、1、2表示晶圆3在这三道工序上分别选择第一台机器、第一台机器和第二台机器。

图2 染色体的编码

接着，按照给定的染色体编码，将晶圆放入工序对应的机器中进行加工，记录每一片晶圆开始加工的时间，以及加工结束的时间，由于机械手一次只能搬运一片晶圆，当遇到冲突时，优先选择前面的晶圆进行搬运。将最后一片晶圆的完工时间作为这批晶圆的总加工时间。

2.2 初始化种群

首先给定种群的初始值size；然后根据晶圆生产规则一道工序只在一台机器上加工的特点，生成一个有n×m个基因的染色体，其中n为晶圆的数量，m为工序的数量，最后使其循环size次，得到一个初始种群。

2.3 适应度函数

适应度函数。适应度函数用于描述染色体对自然界的适应情况，评价个体的质量用晶圆完工时间指标构造适应度函数。

式中：f为适应度函数，Cmax为最后一片晶圆的完工时间。

2.4 交叉操作

交叉操作是种群新个体的主要来源，其结果会直接影响到算法的效率。传统遗传算法中都是采用固定的交叉概率，会存在一些问题：当给定的值较小时会使搜索范围变小，不利于寻找更优解；当给定值较大时可能导致已有的优良染色体在交叉操作后变差。本研究采用自适应的方法调整交叉概率[9]，针对每个染色体优化改进的交叉概率算式如下：

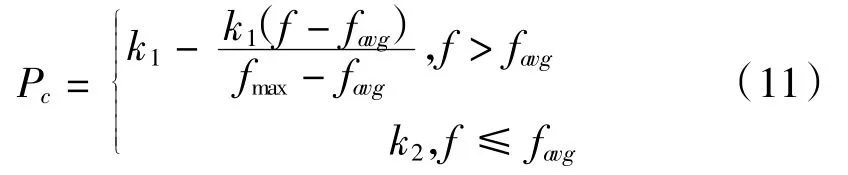
式中：Pc为染色体的交叉概率；噪1、噪2分别为0到1之间的随机数；favg为当前种群中所有染色体的平均适应度值；fmax为当前种群中所有染色体的最大适应度值；f为当前个体适应度值。

此外，交叉操作要保持适中，如果交叉操作使染色体变化过大，则算法将会退化为随机搜索算法，也不利于较优染色体的保留；如果交叉操作不足，使染色体变化不大，则算法失去搜索能力和进化能力[10]。本研究采用多点交叉，实现方法为：将选中的父代个体染色体中随机设置两个交叉点，然后交换两个个体在所设定的两个交叉点之间的部分染色体。两点交叉算子如图3所示。

图3 交叉操作

2.5 变异操作

为了提高变异操作的指导性与精确性，对于不同的染色体采用不同的变异概率，对于优质个体应该采用较低的变异概率与变异方式来进行优良基因的保留，而对于劣质个体应该采用较高的变异概率与方式使其更适于生存[11]。

针对每个染色体优化改进的变异概率计算公式为

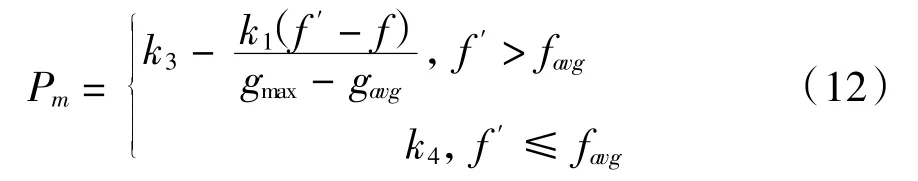
式中：Pm为染色体的变异概率；噪3、噪4分别为0到1之间的随机数；favg为当前种群中所有染色体的平均适应度值；fmax为当前种群中所有染色体的最大适应度值；f′为当前个体适应度值。

采用多点变异，随机生成概率P，若P＜Pm（变异概率），则该染色体发生变异，从染色体中随机选择几个基因，让其在对应工序可加工机器集中重新选一台加工机器。变异操作如图4所示。

图4 变异操作

2.6 选择操作

选择操作即遗传操作后染色体的保留方法。本研究使用轮盘赌进行选择。将所有父代和遗传操作后的子代个体进行混合，并根据适应度函数进行排序，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。通过这种选择方式淘汰垃圾基因，并保持染色体规模的稳定。

2.7 基于遗传算法的调度流程

Step 1：设定晶圆生产调度案例，包括待加工晶圆数量、晶圆的工序数量、满足各工序 生产要求的生产设备；确定遗传算法参数，包括染色体规模、交叉概率、变异概率、算法最大迭代次数等。

Step 2：以随机方式初始化染色体，并计算初始种群平均适应值。

Step 3：按照交叉概率执行两点交叉算子，按照变异概率执行多点变异算子。

Step 4：将父代和子代进行混合，使用轮盘赌选择保留的个体，迭代次数+1。

Step 5：判断算法是否达到最大迭代次数，若否则转至Step 3；若是则输出适应度最大的染色体，算法结束。

3 仿真实验

根据多次实验以及前人实验结果，标准遗传算法的参数设置为：迭代次数为500，种群总大小为100，交叉概率为0.9，变异概率为0.5。改进遗传算法的参数设置为：迭代次数为500，种群总大小为100，k1，k2为0.9，k3，k4为0.12。每种规模的实例优化计算10次，求解的最佳结果如表1所示，求解的平均结果如表2所示。

表1 最佳求解结果比较

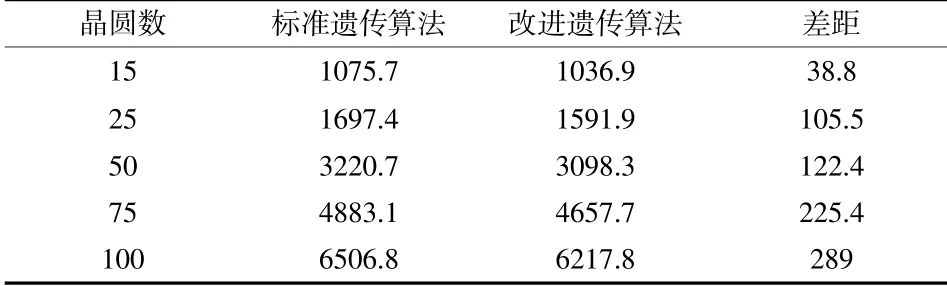
表2 平均求解结果比较

从结果可以看出，改进遗传算法获得的结果始终优于标准遗传算法获得的结果，并且随着加工晶圆数的增加，改进遗传算法获得的结果与标准遗传算法获得的结果的差距越来越大。仿真实验结果有力证明了改进的遗传算法是有效的。

为确定改进遗传算法是否能够在较短的时间内求得调度方案，对算法的运行时间进行了仿真分析，图5可以看出，改进遗传算法的运行时间随晶圆数目的增加基本上呈线性增加，并不会因为数量的增加而导致运行时间呈指数型增长，同时能在较短的时间内求得可行的解决方案，因此，改进遗传算法具有一定的实用性。

图5 算法运行时间

4 结语

本研究的真空锁状态对机械手搬运晶圆的影响，提出的遗传算法为此类集束型设备的调度问题提供了一个行之有效的求解方法。根据机械手调度晶圆选择不同的加工腔加工晶圆，在满足约束的前提下，尽可能使加工晶圆的总完工时间最小。仿真实验结果表明了改进的遗传算法的有效性。