燃料电池性能预测算法的适用性研究

李 超，付建勤，刘敬平，刘 琦

（1.重庆世凯汽车科技有限公司，重庆 401120；2.湖南大学 机械与运载工程学院，湖南 长沙 410082）

0 引言

快速的人口和工业化增长导致传统矿物燃料日益消耗[1]。近年来，氢能以其绿色和不产生污染等优点，已成为最有前景的可再生能源之一[2]。燃料电池作为氢能应用的载体之一，在汽车领域受到广泛关注[3]。因此，对燃料电池发动机性能的准确预测有利于提高动力总成的性能和优化控制策略。

基于机器学习的智能算法在燃料电池性能的预测中拥有着重要地位。叶涵琦等[4]通过构建BP神经网络模型和ELMAN神经网络模型对比分析燃料电池的性能衰减规律，基于约束条件来保证预测精度。高新梅等[5]使用径向基神经网络算法预测不同时域的燃料电池汽车行驶车速，进而探究能量管理策略。以上研究均是在基于某个指定的预测类算法的基础上开展相关优化工作，但并未对预测类算法本身的选取进行合理的比较和探究。

在燃料电池性能预测领域还出现了很多复合算法。Pan等[6]提出一种基于粒子群算法优化的长短期记忆神经网络来对质子交换膜燃料电池进行电堆电压的退化预测，通过使用粒子群算法来提升神经网络的预测效果，但其并未对所选用的预测类神经网络进行过多的对比和研究。

本研究旨在基于燃料电池特有的电化学特性和机理，通过引入自适应学习来最大化的实现各基础预测类模型在燃料电池性能预测中能力，通过对比分析探索适用于燃料电池特有电化学特性的最佳基础预测模型。

1 燃料电池算法模型构建

构建8个常用于燃料电池性能预测的基础模型：BP神经网络、ELman神经网络、模糊神经网络、广义回归神经网络、径向基神经网络、小波神经网络、极限学习机和支持向量机。这些模型常用于燃料电池性能预测的进一步改进，以及复合类模型的基础预测部分。

在这些模型中，BP神经网络是一种多层前馈神经网络，根据预测误差调整网络权值和阈值，从而使模型预测输出不断逼近真实输出，拓扑结构如图1所示，输出层见式（1）。

图1 BP神经网络拓扑结构

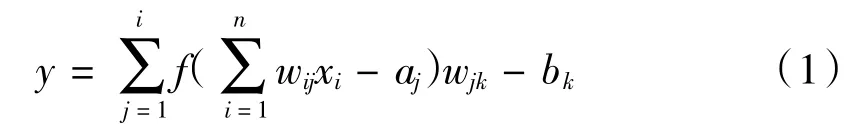
Elman神经网络是常见的反馈式神经网络，它在前馈式神经网络隐含层中增加了一个承接层，作为一步延时的算子用于记忆功能，从而实现对非线性动态过程的实时响应，其结构如图2所示，公式如下：

图2 ELman神经网络拓扑结构

模糊神经网络主要有隶属度和模糊隶属度函数组成。本研究选用的是最常见，且较为成熟的T-S模糊系统，模糊推理通过“If-then”规则形式来定义以实现较强的自适应能力，如图3所示，式（3）为输出函数。

图3 模糊神经网络拓扑结构

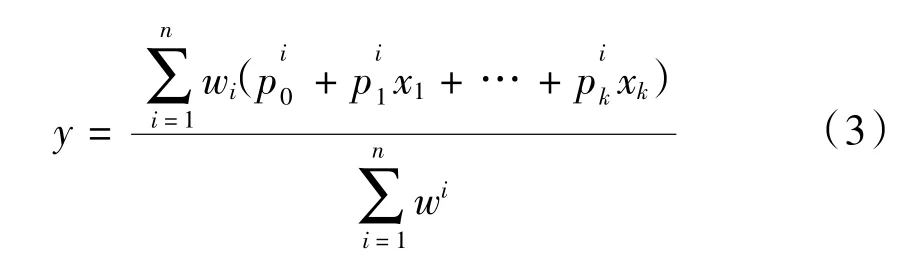
广义回归神经网络在处理少样本和不稳定数据时具有优势。它的柔性网络结构和高度的容错性和鲁棒性使其善于解决非线性映射问题。其是径向基神经网络中一种，如图4所示，输出函数如下：

图4 广义回归神经网络拓扑结构

径向基神经网络是利用径向基函数多维空间插值这一传统技术而来的前向神经网络，它能够使低维空间内线性不可分问题在高维空间内线性可分，因此该网络理论上能够逼近任意非线性函数，结构如图5所示，输出函数如下：

图5 径向基神经网络拓扑结构

小波神经网络以BP神经网络拓扑结构作为基础，通过将BP神经网络的隐含层节点函数替换为小波基函数，从而实现信号前向传播的同时误差反向传播，以此实现对期望输出的精准预测，其结构如图6所示，输出节点见式（6）。

图6 小波神经网络拓扑结构

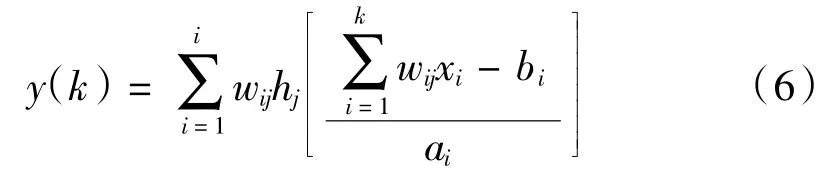
除了以上这些常用的神经网络外，还有一些智能算法也被经常应用于短时光伏预测模型的优化研究上。极限学习机的结构是类似于BP神经网络的前馈结构，如图7所示，输出函数如下：

图7 机械学习机拓扑结构

支持向量机是一种以统计学习作为基础理论的预测模型，其主要思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。支持向量机常用于模式分类和线性回归问题，如图8所示，输出层公式如下：

图8 支持向量机拓扑结构

2 自适应学习因子

在有限的迭代学习次数下，为了避免收敛趋势的减缓，提升各预测模型的收敛精度。本研究特引入自适应学习因子来解决这一问题。各模型预测值的相对变化率表示如下：

其中，i=1，2，…，NP，Xti表示在t次迭代学习中的第i个神经元。（fXti）表示在t次迭代学习中第i个神经元的预测值。（fXtbest）为模型在第t次迭代学习中的最佳预测值，为计算过程中的最小常数，用以避免被除数为零的情况。在第t次迭代学习过程中的第i次传输的自适应因子表示如下：

当存在相近个体时，t次迭代学习过程中的第i次传输的位置向量表示如下：

否则，计算其位置的矢量方程：

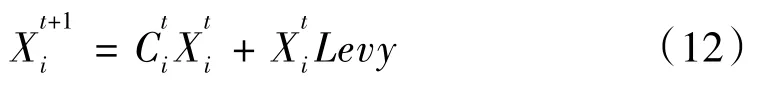
3 模型预测结果

在本研究中，数据来源于团队开展的针对数值模型的验证实验[6]。输出参数为燃料电池的电压，通过极化曲线的形式表现，采样时间为30 s。输入为燃料电池阳极和阴极进出口的流量、温度、湿度、压力以及电池的温度等参数。首先观察通过引入的自适应因子对各个模型预测结果的优化作用，其次对比研究各模型对燃料电池性能输出预测结果。

此外，通过计算各模型预测值的几项评价指标来实现定量分析。评价指标共5项，分别为可决系数（R2）、均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）。R2可以用于表征回归过程的拟合优度，MSE作为基础评估方法可以为后面几种评价方法提供参考，RMSE可以用来衡量预测值与实际值之间的偏差，MAE能够更好地反映预测值误差的实际情况，而通过MAPE可以使这种误差的实际情况变得更加直观利于观察。

3.1 自适应因子优化结果

如图9（a）和9（b），分别表示各基础预测模型在引入自适应因子后的模型预测精度变化情况。从图9可以看出，通过引入自适应因子，各模型的评价指标所量化出的精度均有不同程度的提升，而可决系数R2在五项评价指标中提升最为明显，说明各个模型的综合预测能力均有显著的提升。其中广义回归神经网络引入自适应变异因子后的R2提高最为明显，相较原模型提高19.8%。

图9 自适应因子优化结果

3.2 模型拟合结果

图10（a）和10（b）对比了各个模型对燃料电池电压的预测情况，以极化曲线的形式表征各模型的拟合情况。可以看出，Elman神经网络、极限学习机和BP神经网络在低电流密度区域的预测性能不理想，说明这几类基础预测模型在燃料电池的性能预测中，不擅长处理由活化过电势主导的电化学反应特性的变化。

图10 模型拟合结果

3.3 模型预测结果定量分析

从表2可以看出，广义回归神经网络和BP神经网络的拟合优度均较高，达到了0.97以上，同时表征误差的四项指标也均较低。说明广义回归神经网络和BP神经网络针对燃料电池特有的电化学特性的预测性能较好，模型具备优异的稳定性和鲁棒性。在这二者中，广义回归神经网络的MSE和RMSE最低，而BP神经网络的MAE和RMAE最低，这可能与评价指标本身的特性有关。

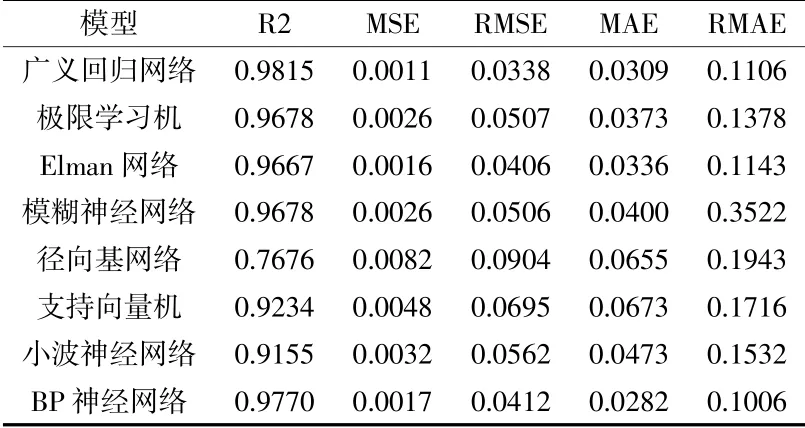
表2 模型预测结果定量分析

4 结语

本研究旨在基于燃料电池特有的电化学特性所产生的数据结构和特点，探明各预测类算法在燃料电池性能预测中的适用情况。

通过引入自适应变异因子来保证各预测类算法在对燃料电池性能预测过程中的精度最大化，以比较各算法对燃料电池性能的极限预测能力。

广义回归神经网络在本次研究中更具有预测优势，模型可决系数高达0.9908，均方误差和平均绝对误差分别低至0.1125和0.1767。结果表明该模型更适宜作为各类针对燃料电池性能预测的基础模型。