基于数值模拟的螺旋锥齿轮搅油功率损失及其敏感度分析

胡 帅，宫武旗，冯 伟，邹天刚，桂 鹏

（1.西安交通大学 能源与动力工程学院，陕西 西安 710049；2.中国北方车辆研究所，北京 100072）

0 引言

车辆的变速器大多采用齿轮传动，齿轮旋转时由于要克服流体阻力做功，一部分的机械能会转化为流体的动能和势能，从而产生能量的损失。近年来，齿轮的传动效率越来越受到人们的关注，因此在设计阶段预测齿轮的功率损失就变得尤为重要。齿轮的动力损耗与润滑密切相关，其功率损失分与载荷有关的功率损失和与载荷无关的功率损失，与载荷无关的功率损失主要包括飞溅，搅动和风阻损失[1]。

近几十年来，许多学者针对齿轮箱的能量损耗参数的影响以及能量损耗机理进行了大量的研究。早期学者使用圆盘来替代齿轮进行搅油试验，研究了圆盘直径和浸油深度对搅油阻力矩的影响，并得到了一个计算搅油损失的经验公式[2]。通过对两组4个不同型号的螺旋锥齿轮进行试验，Larnelle[3]发现浸油深度对搅油损失影响最重要。然而Ho¨hn等[4]通过对齿轮浸油深度进一步的研究发现浸油深度越小，搅油损失越少。Changenet等[5]对小齿轮进行了浸油试验，发现相比于齿的角度和齿面宽，外径是主要影响搅油损失的因素，第二影响因素是齿形，正齿轮和斜齿轮的搅油损失大不相同。强登科等[6]通过试验验证了某型号变速器搅油功率损失，最终得出在黏度较低时，润滑油的温度是影响其搅油功率损失的关键。通过建立空载和加载的计算模型，阚振广[7]对车辆传动系统功率损失进行了系统的分析，并用试验数据进行了验证。霍晓强[8]等人对单齿轮搅油损失进行了试验研究，结果发现油温对搅油功率损失影响并不大。陈晟伟等[9]还发明了一种角度可变的齿轮箱搅油损失试验装置，测试了在倾斜情况下单齿轮的搅油损失。

车载齿轮箱中齿轮旋转速度一般较高，油气两相流运动复杂，可视化较为困难。近年来，随着CFD（Computational Fluid Dynamics）的快速发展，越来越多的学者使用CFD来模拟以及可视化油液在齿轮旋转时的运动状态及分布规律[10]，探讨搅油损失的机理。并以CFD的模拟结果为参考，来改进现有的模型，减少齿轮副的搅油损失。

梁文宏[11]对单个斜齿轮搅油功率损失进行了有限元数值估算，并通过Fluent对其在转动时的三维流场模拟进行了模拟仿真。邹琳等[12]先是利用matlab的PLIC-VOF算法对齿轮搅油功率损失进行了估算，并最终通过数值仿真和试验对估算结果进行了验证，吻合性较好。GORLA等[13]通过CFD仿真发现齿轮箱中润滑油甩离齿轮后，经过一段时间后，又在轴向与齿轮接触，循环周而复始。Liu等[14]使用CFD模拟了行星齿轮的搅油损失情况，并对操作条件例如浸油深度，油液黏度和周向速度进行了说明和讨论，最终在FZG试验台上进行了验证。

以上的工作主要是针对于直齿轮的搅油功率损失的研究，针对螺旋锥齿轮的研究还较少，尤其是对各个影响因素的敏感程度的研究则更少。本研究主要以某车辆变速箱中一对啮合的螺旋锥齿轮为对象，通过正交方案设计和CFD软件对其在不同的共25组工况下进行了全面的数值仿真和讨论分析。研究结果为齿轮箱搅油功率损失的计算及综合传动系统的优化提供了重要的理论参考。

1 数学模型

1.1 质量和动量控制方程

齿轮箱内部流动主要遵循质量守恒方程和动量守恒方程，并且在空气与润滑油均视为不可压缩流体，二者密度不发生变化。控制方程如下：

式中，i，j=1，2，3表示三维流动的三个方向，ρ为流体密度，ui为流体在i方向的速度分量，p为压力，μ为流体动力黏度系数，fi为体积力在i方向上的分量。

1.2 多相流模型

齿轮箱内部空气和润滑油气液两项交界面随时间变化复杂，因此采用VOF（Volume of Fluid）两相流模型追踪其两相流动界面。控制方程如下：

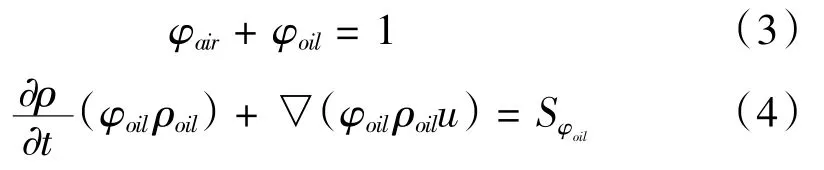
式中，φoil为油相体积分数，φair为气相体积分数，Sφoil为矢量源。

1.3 湍流模型

选用两方程RNG噪-ε湍流模型来处理齿轮箱内部较大的湍流流动问题，其中，湍动能噪和湍流耗散率ε的控制方程如下：

式中，i，j为张量指标，μeff为湍动能的修正项，G噪为由平均速度梯度引起的湍动能，α噪、αε、G1ε、G2ε、G3ε为模型常数。

1.4 扭矩和损失计算

齿轮搅油功率损失分为压力损失和黏性力损失，搅油力矩损失计算公式为：

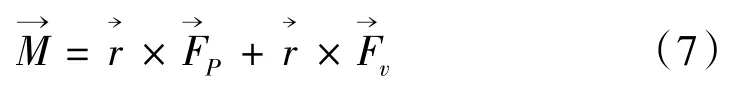
总搅油功率损失计算式为：

2 建模及验证

2.1 数值模型建立

变速箱内部流场是由螺旋锥齿轮副的外壁与变速箱内壁形成的封闭空间，为了便于分析和计算，在保证研究目的的前提下，对齿轮箱进行如下简化：忽略轴和轴承等其他对搅油损失影响较小的部件；忽略齿轮箱内部小结构、螺旋锥齿轮的倒角、圆角等。简化后两种润滑方式的流体域模型如图1所示。

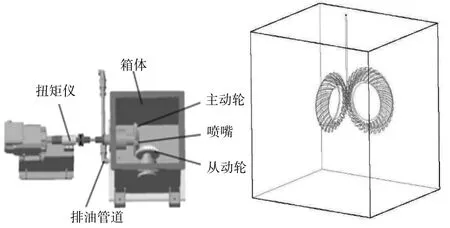
图1 试验台和流体域模型

采用全局四面体网格对流场进行网格划分，并且在齿轮周围和齿轮的啮合处加密网格，如图2所示，这种网格划分方式可以使网格更好地适应几何形状。模拟计算过程中重力的影响也被考虑了。同时，为保证计算的稳定性，在数值计算过程中采用了动网格技术和网格重构技术。在浸油润滑中，流体域的表面设定为壁面；而在喷油润滑中，流体域下表面设定为压力出口。齿轮的表面为动网格的壁面，齿轮旋转运动由Profile定义。模型采用非定常压力基求解。多相流模型选择VOF模型，包含体积力，采用隐式求解。湍流模型选择RNG模型，并且为了提高计算效率，在近壁面处选择应用较为广泛的近壁标准模型。

图2 网格模型

2.2 数值计算有效性验证

采用一对啮合的螺旋锥齿轮在浸油状态下的搅油力矩与现存经验模型进行对比验证，齿轮的详细参数见表1。采用数学模型[15]对计算结果进行验证，仿真环境如下：温度为40℃，油密度为875 kg/m3，油的黏度为8.768×10-2kg/（m·s）。空气密度为1.128 kg/m3，黏度为1.907×10-5kg/（m·s）。主动轮的输入转速为300 r/min，800 r/min和1300 r/min，浸油深度为齿轮中心线下50 mm。在较低转速时，由齿轮旋转而产生的风阻损失很小，可以忽略。

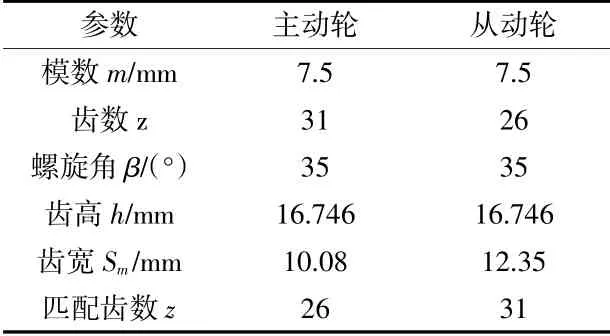
表1 验证所用齿轮详细参数

理论计算和数值模拟的结果对比如图3所示，可以看出数值计算结果与计算出的结果吻合性较高，最大误差仅为9.3%，这表明了数值计算的准确性和可信度。

图3 搅油损失有效性验证

3 正交方案设计

3.1 正交方案设计

为了探究各个影响因素对螺旋锥齿轮搅油损失的影响，并同时确定影响的敏感程度，根据有限元模拟的数据设计正交方案，方案的响应输出为搅油力矩，以转速、油液温度、喷油压力、喷嘴直径和齿轮模数作为考察因素，每个因素设立5个水平，如表2所示。

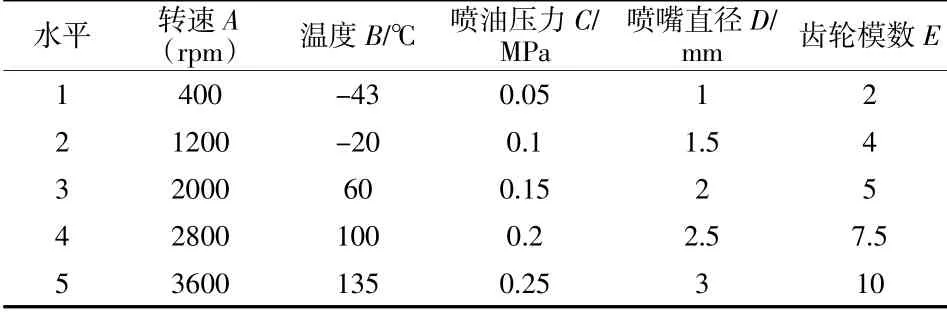
表2 各个因素和水平表

根据各个因素级水平的数据，选取正交矩阵L25（56）设计5因素5水平正交方案，只需取前五列进行正交设计，最终各个因素和水平的分组见表3。

表3 正交设计表

3.2 基于正交方案的螺旋锥齿轮搅油损失影响因素敏感性分析

3.2.1 极差分析

为了减小随机因素的影响，探究各个因素最佳的水平，研究各个影响因素对螺旋锥齿轮搅油功率损失的影响的敏感程度，利用极差分析法对正交方案计算结果进行分析（表4）。

表4中Ti为任一列上水平号为i（i=1，2，3，4，5）时所对应的试验指标和。ti为试验指标的平均值，ti=其中r为任一列上各水平出现的次数。R称为极差，是任一列因素各水平的试验指标最大值与最小值之差。

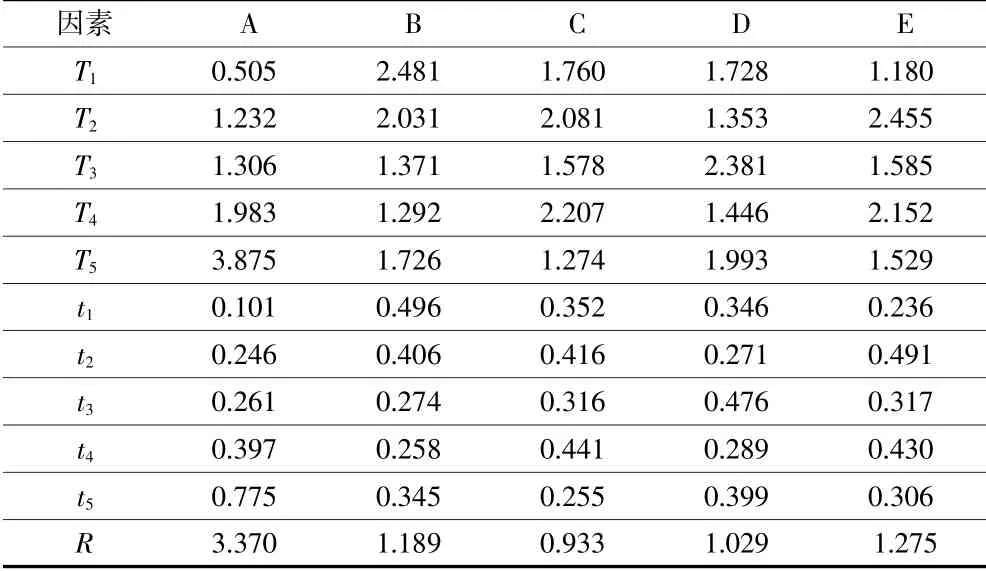
表4 极差分析表

通过计算得到5个因素的搅油力矩M，如图4所示。螺旋锥齿轮的搅油功率损失大小是指齿轮旋转出现较小的搅油力矩，根据图所示可以看出各个影响因素的最优水平，见表5。

图4 搅油力矩均值

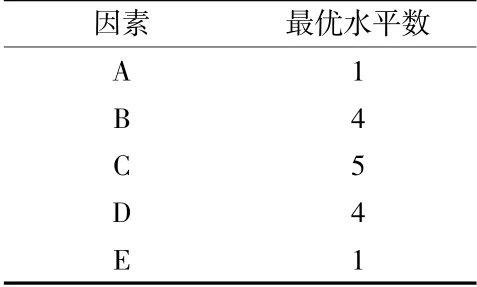
表5 各因素最优水平数

从表5可以看出各个因素的最有水平是非常不同的，利用极差分析来确定各个因素对搅油力矩的影响程度。R值越大，说明该影响因素对螺旋锥齿轮搅油力矩影响程度越大。由表可以看出，各个因素对搅油力矩的影响程度的主次顺序为A＞E＞B＞D＞C。

3.2.2 方差分析

虽然极差分析法的计算量比较小，容易理解，但极差分析同时存在缺陷，无法检验出各因素不同水平间所对应的计算结果差异是由因素水平还是计算误差引起的，同时也不能判断各个因素对螺旋锥齿轮搅油力矩的影响程度。因此采用较为复杂的方差分析法来弥补极差分析法的不足并进行方差分析的F检验，评估了各个因素的影响显著性。

各个因素的偏差平方和见表6，表6中f为因素的误差自由度，m为均方差。Fa（x，y）中a代表各个因素的显著性水平，x和y分别代表各个因素和误差的自由度，a为0.005，0.01，0.025，0.05，0.10，其代表的置信几率分别为99.5%，99.0%，97.5%，95.0%，

表6 F值检验表

90.0%。

当FA≥F0.01（x，y）时，表示A因素的变化对螺旋锥齿轮搅油力矩变化影响高度显著；当F0.01（x，y）＞FA≥F0.05（x，y）时，表示A因素的变化对螺旋锥齿轮搅油力矩变化影响较为显著；当F0.05（x，y）＞FA≥F0.10（x，y）时，表示A因素的变化对螺旋锥齿轮搅油力矩变化有影响；当F0.01（x，y）＞FA时，表示A因素的变化对螺旋锥齿轮搅油力矩变化影响不显著。该规律同样适用于B、C、D、E因素。

经查F值分布表得，F0.01（4，4）=15.977，F0.025（4，4）=9.6，F0.05（4，4）=6.39，F0.10（4，4）=4.11。由表6可以看出A因素的变化对螺旋锥齿轮搅油力矩变化影响较为显著，远大于其他各个因素，剩余4个因素对螺旋锥齿轮搅油力矩变化影响都不显著。并且从表中F值的大小可以得到各个因素对搅油力矩的影响顺序为A＞E＞B＞D＞C，这与极差分析得出的结论一致，证明了极差分析研究搅油力矩影响程度主次顺序的准确性。

4 结语

采用计算流体动力学的方法计算了一对啮合的直齿轮空载时在喷油润滑状态下的搅油功率损失，基于正交设计方案，通过极差分析和方差分析讨论了各个因素对搅油力矩的影响，所得结论如下：

（1）齿轮搅油功率损失的仿真结果与理论公式计算结果数据相近，表明了使用计算流体动力学方法预测齿轮搅油功率损失的可靠性和有效性。

（2）通过极差分析，得出转速、油液温度、喷油压力、喷嘴直径和齿轮模数的最优水平分别为1、4、5、4、1，并且各个因素对搅油力矩的影响程度的主次顺序为转速、齿轮模数、油液温度、喷嘴直径、喷油压力。

（3）通过方差分析，转速的变化对螺旋锥齿轮搅油力矩变化影响较为显著，远大于其他各个因素，剩余4个因素对螺旋锥齿轮搅油力矩变化影响都不显著。

（4）极差分析和方差分析得出的灵敏度影响顺序一致，证明了极差分析研究搅油力矩影响程度主次顺序的准确性。