等腰三角形中不确定性问题解决思路探究
⦿甘肃省庆阳市宁县第五中学 陈秀莲
1 引言
结合二十余年的教学经验发现,等腰三角形中不确定性问题的解决,困扰了很多学生,学生在此问题中经常出现错解、漏解.其实,归根结底这是逻辑思维能力弱的表现.那么,如何借助等腰三角形中不确定性问题解决思路的探究培养学生的逻辑思维能力呢?本研究从两道易错题出发,通过纠错辨析为这类问题探寻正确解决方法奠定基础.
2 易错题及其纠错评析
例1若等腰三角形一腰上的高与另一腰的夹角为40°,则顶角的度数为.
错解:因为等腰三角形一腰上的高与另一腰的夹角为40°,所以这条高和另一腰之间的夹角与这个顶角之间一定互余,因此顶角的度数为90°-40°=50°.
纠错:该生解题时,由于出现了思维定式,习惯性地认为这个等腰三角形是锐角三角形.事实上,等腰三角形分为三种,它们的顶角分别是锐角、直角和钝角.在本题中,根据题意可以排除顶角为直角的情况,因此剩下顶角为锐角、钝角两种情况,需要分类讨论.具体过程如下:
解:在△ABC中,AB=AC.本题有两种不同情况:
当顶点A为锐角时,如图1所示,作BD⊥AC,垂足为D.因为∠ABD=40°,所以∠A=90°-40°=50°;
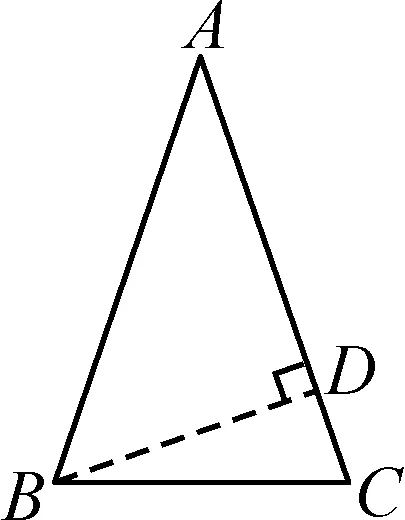
图1
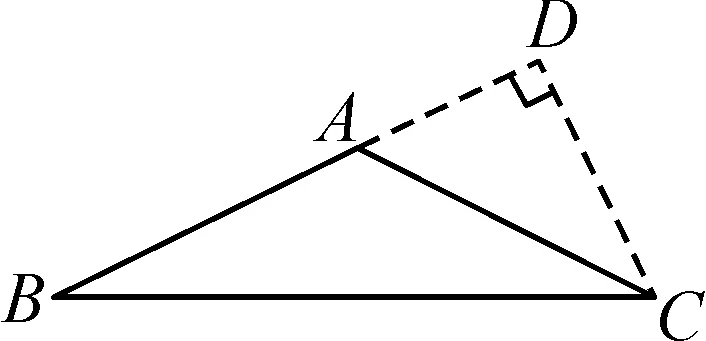
图2
当顶角∠BAC为钝角时,如图2所示,作CD⊥BD,交BA的延长线于点D.因为∠ACD=40°,所以∠BAC=90°+40°=130°.
综上所述,顶角的度数为50°或130°.
评析:在解决初中数学问题过程中,思维定式是阻碍学生顺利解决问题的原因之一.要突破这种思维,首先要培养学生从多个角度思考问题的习惯,让学生多用不同的方法解决问题,以激发他们的思维,其次重点关注题目所给条件中的关键词语,如腰、顶角、底边等,深入思考它们是不是存在多种可能,特别是能否画出多种情况对应的图形[1].
例2若等腰三角形的周长为16 cm,其中一边长为4 cm,则该等腰三角形的底边长为( ).
A.5 cm B.4 cm
C.8 cm D.4 cm或8 cm
错解:因为等腰三角形的周长是16 cm,且其中一边长为4 cm,也就是腰为4 cm,所以底边长就是16-2×4=8 cm,故选:C.
纠错:从上面错解过程可以看出,该生习惯性地认为这条边是等腰三角形的腰.事实上,等腰三角形的边可以是腰,也可以是底边.本题中只告诉了“一边长”,而并未明确这条边是腰还是底边.所以,将长为4的这条边认为是等腰三角形的腰,又是出现了思维定式的问题.因此,应该分类讨论,具体过程如下:
解:根据题意,本题有两种不同情况.
如图3所示,当长为4 cm的边为等腰三角形ABC的腰时,BC就是底边,且BC=16-2×4=8 (cm).但是,此时的三条边不能构成一个三角形,更不能成为等腰三角形,所以这种情况应该排除;
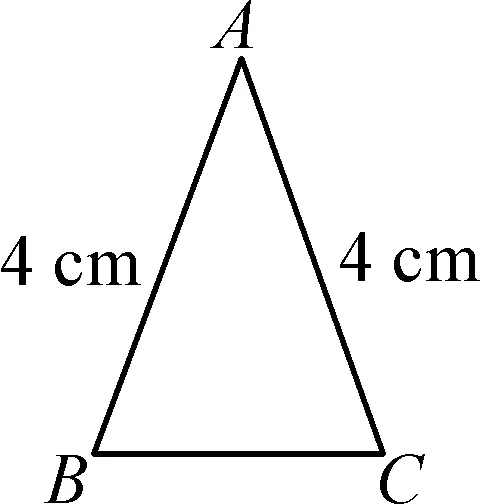
图3
如图4所示,当长为4 cm的边为等腰三角形的底边时,BC=4 cm.此时,两腰长为6 cm,能够构成符合题意的等腰三角形.

图4
综上所述,它的底边长4 cm.故应该选:B.
评析:学生在解决例1和例2时,都容易因为思维定式导致漏解、错解现象.与例题1不同的是,本题除了要根据等腰三角形边的类型分为两种情况讨论之外,还需要分析这两种情况中的三边是否能构成三角形,这一点又是学生极易忽略之处.为此,教师在教学时仍应将培养学生缜密的逻辑思维作为本节课的教学重点,并且在后阶段一以贯之.只有这样持续进行下去,学生才能有较大改变[2].
3 等腰三角形中不确定性问题的类型及解决思路
等腰三角形是一种比较特殊的三角形.根据角的类型,可以分为等腰锐角三角形、等腰直角三角形和等腰钝角三角形,它们的顶角分别是锐角、直角和钝角[3].根据边的类型,可以分为一般等腰三角形和特殊等腰三角形(等边三角形).基于等腰三角形中角和边的类型均多样化,等腰三角形中不确定性问题主要有以下几种类型.
3.1 角不定型
根据等腰三角形的性质可知,等腰三角形的两底角相等.再结合三角形的内角和为180°,所以两个底角一定是锐角.然而等腰三角形的顶角只有一个,它可能为锐角、直角,也可能为钝角,这是造成等腰三角形中不确定性问题的原因之一.结合教学经验来看,有很多题目在呈现等腰三角形的角的条件时,并不直接说明该角是顶角还是底角,那么这类问题应该如何解决呢?下面结合例题3说明这类问题的解决思路.
例3若等腰三角形的一个角为40°,那么另外两个角的度数分别是.
分析:本题只给出了等腰三角形中的一个角,并未说明该角是顶角还是底角.所以解决思路如下:
首先,明确边角问题.本题是关于等腰三角形的角的问题.
其次,明确角的类型.本题给出的角不够明确,所以可能是顶角,也可能是底角.
再次,分类讨论:对该角是顶角、底角两种情况分别讨论.
最后,综述.分类讨论后一定要进行综合.
解:由于等腰三角形(△ABC)中40°角可能是顶角,也可能是底角,故有以下两种不同的情况.
(1)当40°角是顶角时,如图5所示,∠B=∠C=(180°-40°)÷2=70°;
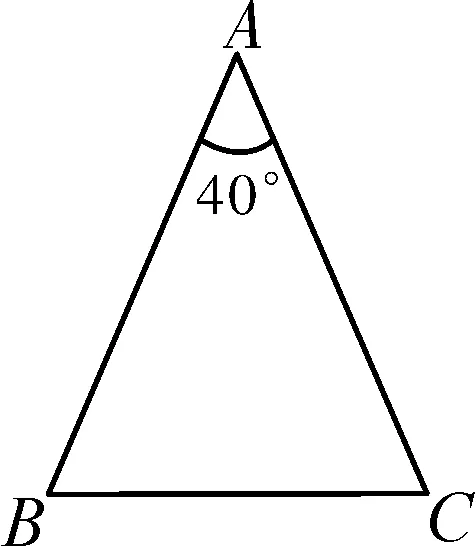
图5
(2)当40°角是底角时,如图6所示,∠A=180°-40°-40°=100°.

图6
综上所述,另外两个角的度数分别是70°,70°或40°,100°.
3.2 边不定型
等腰三角形中的三条边,一类是腰,一类是底边.根据等腰三角形的性质可知,等腰三角形的两腰相等.结合教学经验来看,有很多题目在给出等腰三角形的边的条件时,并不直接说明该边是腰还是底边,继而造成了等腰三角形中不确定性问题.那么这类问题应该如何解决呢?下面结合例题4说明这类问题的解决思路.
例4已知实数x,y满足|x-4|+(y-8)2=0,则以x,y为两边长的等腰三角形的周长为.
分析:本题可通过“|x-4|+(y-8)2=0”计算出x,y的值,即得到了等腰三角形两边长.但由于并未说明这两边是腰还是底边,所以要按照如下思路解决.
首先,明确边角问题:本题是有关等腰三角形的边的问题;
其次,明确边的类型:本题给出的边不够明确,所以可能是腰,也可能是底边;
再次,分类讨论:对该边是腰、底边的两种情况分别讨论;
最后,综述:分类讨论后一定要进行综合.

图7
解:因为|x-4|+(y-8)2=0,所以x=4,y=8.由于给出的边不够明确,所以可能是腰,也可能是底边,故分以下两种不同的情况.
(1)当腰为4,底边为8时,此时的三条边不能构成一个三角形,更不能成为等腰三角形,所以这种情况应该排除;
(2)当腰为8,底边为4,此时的三条边能构成三角形,且它为等腰三角形,如图7所示.所以,三角形的周长为8+8+4=20.
综上所述,以x,y为两边长的等腰三角形的周长为20.
4 结语
综上所述,无论等腰三角形种不确定问题属于哪种类型,分类讨论思想是解决这类问题的重要方法.无论学生在解决哪种类型题目的过程中出现了错误,都暴露出了思维定式的问题.所以,作为初中数学一线教师,不仅要凭借更丰富、灵活的变式训练学生的思维,让他们突破思维定式的瓶颈,而且要将这种训练方式一以贯之,如此学生才会形成更强的思维能力、更有效的灵活性.

