谈如何构建生机勃勃的数学复习课堂
⦿甘肃省武山县渭北初级中学 高 芳
1 引言
在数学教学中,大多数教师在讲授新知时往往会根据教学内容设计多种教学模式来活跃课堂,激发学生学习热情,如:演示式、探究式、讲授式等,然而在章节复习时却仅应用单一的“讲授式”,课堂由教师主导,执行教学“一言堂”,学生的主体作用得不到发挥,师生的互动也仅限于“问答”,教学模式单一、僵化,学生处于被动学习状态,课堂效率低下[1].究其原因主要是教师对复习课的作用认识不够,将复习课的重心放置于解题技巧和解题方法的探究与强化.事实上,解题只是复习课的一部分.复习课有着更为广泛的教学目的:利用复习课从整体上将相关知识点横纵编织,形成一个大型的知识网络,以实现知识的迁移;利用复习课查缺补漏,教师根据作业及试卷反馈将普遍存在的问题重点讲解,以弥补教学漏洞;利用复习课在夯实基础的前提下,进行拓展和提升,进而开阔学生视野,提升综合解题能力.可见,教师若仅将复习课定义为普通的习题课,就很难发挥复习课的优势.那么,复习课如何上才更有效呢?笔者在复习一元二次方程解法时坚持以学生为主,通过师生互动、合作探究,优化课堂结构,提升课堂有效性.现将教学过程与大家分享,仅供参考.
2 课前准备
充分的课前准备是上好数学复习课的前提和保障.在日常教学中,大多数教师引导学生根据教材目录回顾旧知,通过小组合作的方式对知识进行梳理,进而为系统建构奠基.这里,为了使课堂更加生动,笔者借助多媒体教学的优势,通过简短的微课引导学生课前自主建构,自主完善[2]知识体系.
2.1 观看微课
授课前,笔者根据教学内容精心设计了微课,让学生先自学相关内容,将有关知识串联编织成简单的网络形成初步认识.
2.2 完成练习
(1)解方程:
①(x+1)(x+3)=15;
②343x2+342x-685=0;
③5x2-7x-6=0;
④-2x2+9x=9.
(2)求方程x2-x-1=0的近似解(精确到小数点后两位).
(3)用图象法求一元二次方程2x2+x=7的近似解(精确到0.1).
为了使听课更具目的性和针对性,教师设计了运用不同方法求解一元二次方程的题目,让学生通过自主检测发现问题,进而提升听课效率.
通过观看微课和自主检测,学生对本课的重难点有了基本的了解,为更好地参与课堂教学做好了充足的准备.
3 教学实录
课前学生对本节课已经有了整体的认识,为了更好地发挥学生的主体作用,调动其参与的积极性,在教学过程中教师通过师生和生生互动,合作交流来完成一元二次方程解法的探究.
3.1 问题初探,寻找解决问题的一般方法
师:本节课的教学目标大家都很清楚了,请问,解一元二次方程可以应用哪几种方法呢?(学生有了课前充足的准备,回答问题时游刃有余.)
生1:可以直接应用公式法,有些特殊的还可以采用直接开平方法、配方法和因式分解法.
生2:图象法也可以.
师:很好!这么多方法,如果让你选择,你会优先选择哪个呢?
生3:根据题目特征,一般从直接开平方法、配方法和因式分解法入手,若这几种方法都很难求解时,可以用公式法,最后考虑图象法.
师:为什么要将图象法放在最后呢?(教师追问)
生3:因为图象法不仅绘制时需要较多的时间,而且其求出的值也很难得到精确值.
师:有道理!课前我们在解(x+1)(x+3)=15时,大家运用了什么方法呢?
生4:先将其化为一般形式x2+4x-12=0,再因式分解得(x-2)(x+6)=0,因此得出x1=2,x2=-6.
师:很好.还有其他方案吗?
生5:直接用公式法求解.
师:也是一个办法,但是相对于这个题,公式法计算量会更大一些.还有更简单的方法吗?(学生又开始寻找第三个解决方案.)
生6:我的方法不知道是否正确.因为x+1 师:非常好!通过观察和猜想就轻松求解了.接下来看下一题,343x2+342x-685=0又该如何求解. 学生最初都认为此题应该用公式法求解,但在求解时却发现计算量过大,且开方困难,所以很难得出答案.虽然公式法在解题时最直接,但是不一定是最佳方案,学生解题碰壁后尝试用新的方法求解,很快有了新发现. 生7:用生6的观察法,因为343+342=685,所以方程的一个根为1,再根据根与系数的关系可以求解另外的根. 师:非常好! 生8:可以用十字相乘法. 学生在求解碰壁后,并没有放弃,而是另辟蹊径找到了更加方便的解决方案.学生的解题思路在不断的交流中慢慢打开. 教师让学生合作探究方程5x2-7x-6=0和-2x2+9x=9的解法.通过交流发现,虽然求解的方法有很多,但是最为通用的是公式法.公式法在解题中很重要,只要Δ≥0都可以用此方法求解. 在复习教学时,学生对题目已经形成了较为完善的认识,引导其通过合作交流,让不同思维相互碰撞产生火花,从而点燃课堂[3]. 师:现在请小组合作探究,一起完成问题(2). 师:如果不能用计算器,那么还能求解吗?(教师追问) 生9:若是其他值,没有计算器好像无法求解. 师:是个很好的方法,也很有创意,大家认为怎么? 生11:虽然方法很好,但是操作会相对复杂,不容易把握,我感觉图象法应该更为直观、通用. 师:看来有必要一起探究一下图象法了,现在请大家看看如何用图象法来求解问题(3).(教师给学生足够时间进行图象绘制和求解.) 生12:画抛物线y=2x2+x-7的图象,该抛物线与x轴交点的横坐标即为方程2x2+x=7的近似解. 生13:画抛物线y=2x2+x和直线y=7的图象,抛物线与直线交点的横坐标就为所求. 生14:还可以画y=2x2与直线y=x-7的图象. 师:都是非常好的办法,那么哪一个才是最优方案呢?(教师话音刚落,学生就开始抢答了.) 生15:生13和生14的方案好,图象更容易绘制. 师:哪个方案可以作为通用方案呢? 生16:生14的方案较为通用,因为任何方程都可以化简为x2=px+q的形式,所以最后一个方案最通用. 在整个教学过程中,教师以问题为引导,充分发挥学生的主体作用,让学生通过合作交流加深了对各种解法的理解,而且还总结归纳出了通用方法.通过探究,学生可以清晰地发现,每个解法都有其优势也有其不足,因此在解题时必须会观察,善于根据方程特点选择合适方法,有时可以让多种方法相结合,进而扬长避短. 复习课是数学课堂教学的重要组成部分,教师必须引起足够重视,切勿盲目用“题海”影响复习课堂优势的发挥.本节教学活动中,成功应用了“翻转课堂”,让学生充分做好课前准备,为课内的合作交流、以及知识体系形成打下了坚实的基础.另外,从上面的教学实录可以看出,课堂气氛活跃,学生不仅积极回答问题而且积极参与合作探究,学生的学习能力和思维能力得到了较好的发展.同时,教师适时地提问,适当地引导和评价,充分发挥了其主异作用.通过师生和生生的平等互动交流推动了课堂发展,教学更加生动、高效. 总之,要打造高效、高质的数学课堂需要教师精心筹备,无论课前、课中还是课后都要精心预设,以此来调动学生学习的积极性,使学生在合作交流中相互促进,共同成长.3.2 合作提升
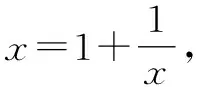
4 教学反思

