巧构参数方程 妙解数学问题

⦿甘肃省张掖市肃南裕固族自治县第一中学

张 超

1 引言

参数方程是解决直线、圆锥曲线等相关平面解析几何问题中曲线比较常用的一种表达方式.巧妙构建直线、圆锥曲线等的参数方程，相比对应的普通方程有时可以更加简捷方便地表示问题，从而简化运算，优化过程，提升效益，有助于学生进一步体验数学方法的灵活多变.

2 直线的参数方程问题

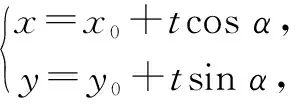
例1[2022届清华大学中学生标准学术能力诊断测试(2021年11月测试)数学文科试卷·8]已知圆C：x2+y2-8x-4y+19=0，直线l：3x-2y-6=0，直线l交圆C于A，B两点，设点P(2，0)，则|PA|·|PB|=( ).

分析：根据所求的关系式|PA|·|PB|的特征，合理联想到直线的参数方程中参数的几何意义，将直线的一般方程转化为过点P的参数方程，结合参数方程的代入与转化来确定相应的含参二次方程，利用参数的几何意义解决问题.

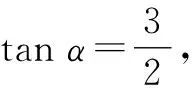
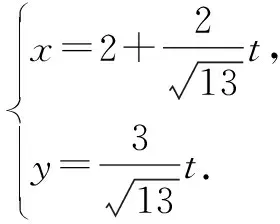
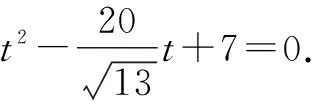
所以，|PA|·|PB|=t1t2=7.故选择答案：D.

点评：在求解一些有关距离或线段的长度问题时，可巧妙引入直线的参数方程，根据相关参数的几何意义来直接转化与处理.方程化解决，整体化思维，可以很好避免求解具体点的坐标、以及线段的长度等相关问题.

3 椭圆的参数方程问题

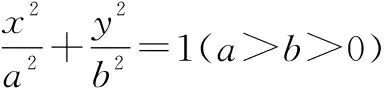
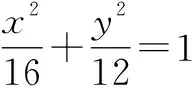
分析：结合椭圆的参数方程进行三角换元，代入所求的分式代数式，通过变形与转化得到相应的三角关系式，结合函数的构建以及求导处理，利用导函数为零确定相应三角关系式的最值，进而确定分式的最小值.

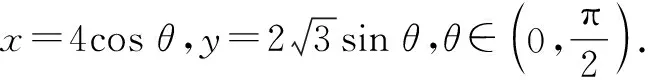
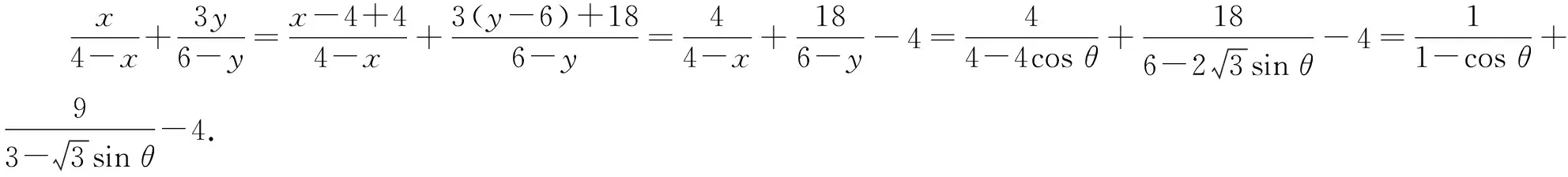
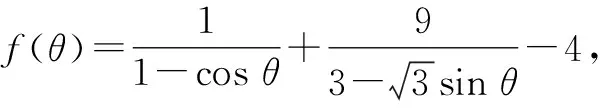
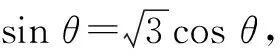
所以，f(θ)的最小值为

故填答案：4.

点评：解决一些涉及圆锥曲线上的点所对应的代数关系式的最值或取值范围问题，通常可以巧妙引入圆锥曲线的参数方程，比用普通方程更简捷方便，进而转化为相应的三角函数的最值或取值范围问题.

4 双曲线的参数方程问题

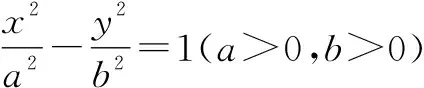
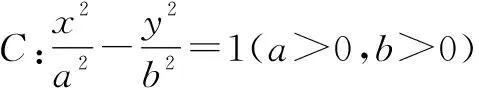
(1)求C的离心率；

(2)若B在第一象限，证明：∠BFA=2∠BAF.

分析：(1)根据题目条件中两直线的垂直关系，结合点的坐标，从距离关系入手，建立相应参数之间的关系式，通过求解方程确定双曲线的离心率.(2)结合双曲线的参数方程进行三角换元，通过斜率公式以及三角恒等变换，巧妙转化，合理证明.

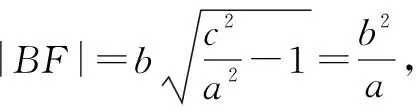
又c2=a2+b2，所以c2-ac-2a2=0，即e2-e-2=0，解得e=-1(舍去)或e=2.

所以，双曲线C的离心率为2.

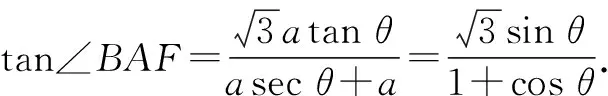
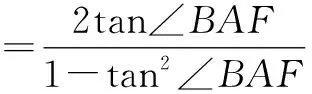
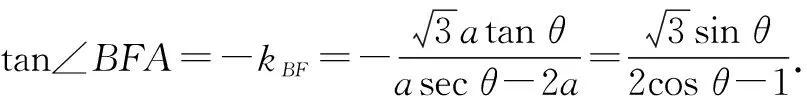
因此tan2∠BAF=tan∠BFA，即∠BFA=2∠BAF.

当|BF|=|AF|，且BF⊥AF时，∠BFA=2∠BAF=90°.

综上所述，若B在第一象限，∠BFA=2∠BAF.

点评：解决一些涉及圆锥曲线中的角的关系问题时，自然联想到圆锥曲线的参数方程，其中含有角与对应的三角函数值问题，合理构建参数方程中的角与平面几何解析中相关概念以及角之间的关系，结合三角函数的相关知识来分析与处理，目的更加明确，操作起来更加简单快捷.

5 抛物线的参数方程问题

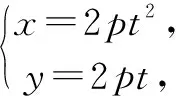
例4在平面直角坐标系xOy中，F为抛物线Γ：y2=2px(p>0)的焦点，点B在x轴上，且在点F的右侧，点A在Γ上，且|AF|=|BF|，直线AF，AB与Γ的第二个交点分别为M，N，若∠AMN=90°，则直线AF的斜率为________.

分析：根据抛物线的参数方程设出对应点的坐标，结合两直线垂直所对应的斜率关系式建立方程，进而确定参数值，从而得以求解直线的斜率.

解析：设A(2pt12，2pt1)，M(2pt22，2pt2)，N(2pt32，2pt3).

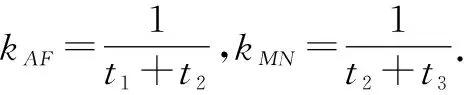
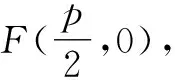
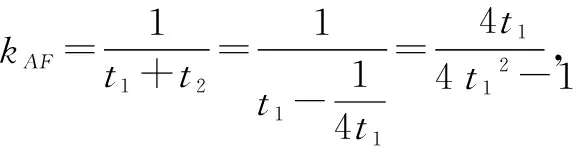
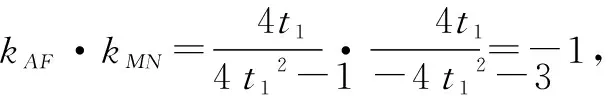
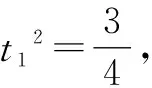
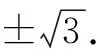
点评：解决一些涉及圆锥曲线上的概念、轨迹等问题时，利用圆锥曲线的参数方程自然巧妙地引入参数，通过函数与方程思想等来巧妙转化，实现相关参数的确定与求解、关系式的确定等，从而简单快捷处理相应的圆锥曲线问题.

6 变式练习

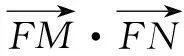
A.-4 B.-5 C.4 D.不确定

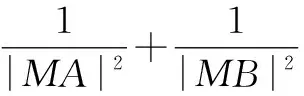
A.1 B.2 C.3 D.4

(3)已知点M到点F(3，0)的距离比它到直线l：x+5=0的距离小2.

①求点M的轨迹E的方程；

②过点P(m，0)(m>0)作互相垂直的两条直线l1，l2，它们与①中轨迹E分别交于点A，B及点C，D，且G，H分别是线段AB，CD的中点，求△PGH面积的最小值.

7 结束语

利用参数方程来解决直线、圆锥曲线等相关平面解析几何问题，思维巧妙，往往能化繁为简，迎刃而解，起到事半功倍的效果.既能锻炼学生的逻辑思维，拓宽解题思路，培养学生“一题多解”的能力，又能激发他们的潜能，潜移默化地渗透数学思想方法，提高学习积极性，提升主动探索实践的能力.