不同版本教材“诱导公式证明”的比较研究

⦿西华师范大学数学与信息学院

胡奇云

⦿绵阳东辰国际学校

陈文静

1 引言

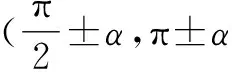
2 不同版本教材中诱导公式的证明分析

2.1 新人教A版的证明特点

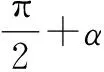
2.2 旧人教B版的证明特点

教材首先证明了角α与α+k·2π(k∈Z)的三角函数关系，观察该公式特征，进行猜想，进而研究角α与α+(2k+1)π(k∈Z)的三角函数间的关系.结合这两个公式，推陈出新，得到角α与α+nπ(n∈Z)的三角函数间的关系：角α与α加上π的偶数倍的同名三角函数值相等；角α与α加上π的奇数倍的正弦、余弦值互为相反数，角α与α加上π的奇数倍的正切值相等.归纳总结公式，有利于学生理解与记忆，并培养良好的学习习惯.

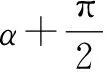
2.3 新人教B版的证明特点

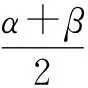
公式证明最后，均以相应的三角函数线之间的关系进行辅佐，学生动手操作，关联旧知，互相结合加深印象，避免死记硬背公式.

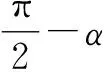
2.4 北师大版的证明特点

教材内容分为诱导公式与对称、诱导公式与旋转两部分，直观展现了诱导公式的两种证明方法，并以此将诱导公式进行分类.相较于其他版本，北师大版教材中各诱导公式的证明标题更加明确，主体突出，如“角α与-α的正弦函数、余弦函数关系”，证明结论也没有顺势给出相关的正切函数，使知识点更加聚焦.

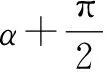
2.5 湘教版的证明特点

教材通过已证得的诱导公式来推导证明角α与π-α的三角函数关系，也提示学生从两个角的终边关于y轴对称来探究，又继续引导学生借助单位圆的三角函数线来研究，证明方法不再局限于一种，锻炼学生的逻辑推理能力，有利于思维的发展.

2.6 各个版本教材证明的共同点

(1)证明过程均利用单位圆的对称性.三角函数具有奇偶性，而奇偶性也是对称性的一种形式，故三角函数也具有这些性质[3].圆最特殊和最重要的性质就是对称性，所以利用圆的对称性来研究三角函数的对称性，符合2017年版课程标准要求.在单位圆中，两个终边具有对称性的角，其与单位圆的交点亦具有对称性，根据交点坐标的特征即证得诱导公式.

(2)对于研究角α与α+k·2π(k∈Z)的三角函数间的关系，以上版本教材都是依据三角函数的定义证明，衔接旧知，体现定义的基础性与导向性.

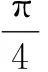
(4)各版本教材均归纳了公式间的共同特征，将其一般化，总结概括为法则并明确用途.

3 课堂教学建议

3.1 对比教材，进行互补

3.2 自主探究，合作交流

证明诱导公式的思路和方法有多种，且有很强的逻辑性.课堂上教师可以让学生自己动手证明，或小组合作探究.引导学生仔细观察，猜测分析角之间的关系，激发学生的创新思维，提升学生数学学习的兴趣.推理过程也能帮助学生内化数学知识和领悟数学思想，防止学生思维僵化和教学“满堂灌”的现象，符合学生身心发展的需要.

3.3 关联知识，注重联系

诱导公式安排在三角函数定义之后，教师应在教学过程中注意新旧知识点的联系和衔接，由浅入深带领学生感受诱导公式的重要作用以及单位圆在三角函数中的重要性，强化对知识点的理解[4].另外，初中阶段初步认识的锐角三角函数，在证明过程中也能用来引导学生进行关联，从特殊到一般，加深情境印象，巩固知识结构.

4 总结与反思

诱导公式揭示了终边具有某种关系的两个角的三角函数值之间的关系.各版本教材使学生基于单位圆从角终边的对称性的角度深刻理解并运用诱导公式，体会对称的作用.诱导公式的证明体现了数学中的简化思想、化归思想和数形结合思想.如何合理有效地将不同版本教材的特点运用于教学活动中，使课堂效率最大化，还有待研究.