精心组织教学活动 促进核心素养提升
——以“函数与方程(一)”为例
江苏省海门中学
姜璐璐
数学教学应坚持以生为本,引导学生通过观察、发现、归纳等数学活动掌握基本知识和基本技能,在解决问题的过程中形成经验,从而在知识和经验的共同作用下形成学习能力.笔者在“函数与方程(一)”教学时,借助情境和问题设计教学活动,在培养学生观察能力、概括能力、抽象能力等方面取得了较大突破,与大家分享,以期共鉴.
1 教学分析
“函数与方程(一)”是一节抽象的概念课,重点是理解和掌握函数零点定义及零点存在性定理.概念课看似简单,但受传统教学模式影响,在教学中常出现“重结论,轻过程”的现象,从而将“概念课”变成了“习题课”,学生知道个一知半解就忙着去应用,结果后期解决综合性问题时漏洞百出.要让学生真正将概念学懂吃透,既清楚内涵又了解外延,需要教师精心预设.本节课在问题情境的引领下,旨在培养学生的观察、抽象概括能力,体验函数与方程、转化与化归、数形结合等重要数学思想的应用,从而提升数学核心素养.
2 教学活动设计
2.1 回顾旧知,引出新知
教学片段1:
师:利用对数知识求方程0.84x=0.5的近似解,该如何求呢?
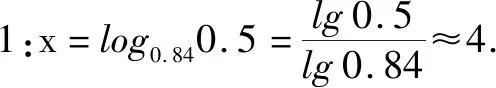
师:很好!如果利用图象,你能求吗?
生2:可以求.将方程0.84x=0.5左右两边看作两个函数,y=0.84x和y=0.5,两函数y=0.84x和y=0.5图象交点的横坐标即为所求.
师:很好.生2通过构造法构造了两个较为熟悉的函数y=0.84x和y=0.5,这样在同一直角坐标系中作出函数图象,借助图象可求方程近似解.
设计意图:函数与方程都是高中数学重点内容,在数学中占有重要的位置,同时两者又有着紧密的联系.如果教学之初就直接指出两者的联系似乎有些生硬,为此,先用旧知“对数相关知识”来引入,引导学生用代数的思路直接求解.接下来,运用问题“如何利用图象求解”,引导学生联想函数,由此将方程转化为了函数,这样引入新课题也就水到渠成了.
2.2 借助特例,归纳提炼
教学片段2:
师:观察以下几个特殊函数的图象,试写出函数图象与x轴交点的坐标,并求出对应方程的根,看看你有哪些发现.
①一元二次方程x2-2x-3=0与函数y=x2-2x-3(图象如图1);
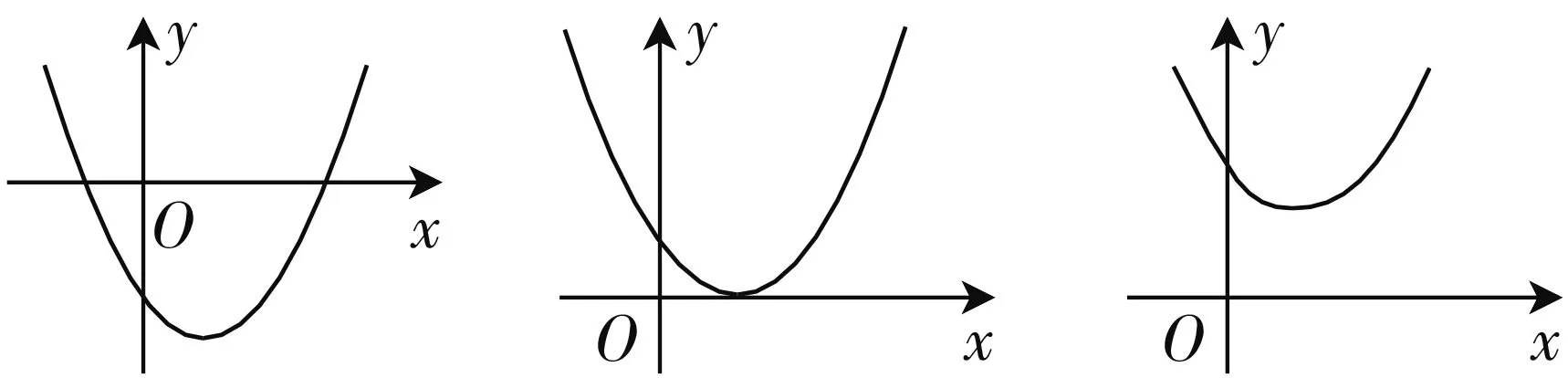
图1 图2 图3
②一元二次方程x2-2x+1=0与函数y=x2-2x+1(图象如图2);
③一元二次方程x2-2x+3=0与函数y=x2-2x+3(图象如图3).
问题给出后,教师预留时间让学生进行观察,并引导学生应用数学语言进行总结和归纳,很快,很多学生迫不急待的想发表自己的见解了.
生3:分析第①组,该一元二次方程有两个根,分别为-1和3,与之相应的函数图象与x轴的交点坐标分别为(-1,0),(3,0).由此可知,方程x2-2x-3=0的根即为函数y=x2-2x-3与x轴的交点的横坐标.
生4:在第②组中,方程的根为x1=x2=1,相应的交点坐标为(1,0),故与生3得出的结论类似.
生5:在第③组中,方程没有实数根,图象与x轴无交点.
师:大家说得非常好!刚刚我们观察的是特殊方程,如果对于一般方程会有怎样的结果呢?请各小组分工协作,完成下面表格(如表1).(学生已经发现了一般规律,很快完成了表格的填写.)
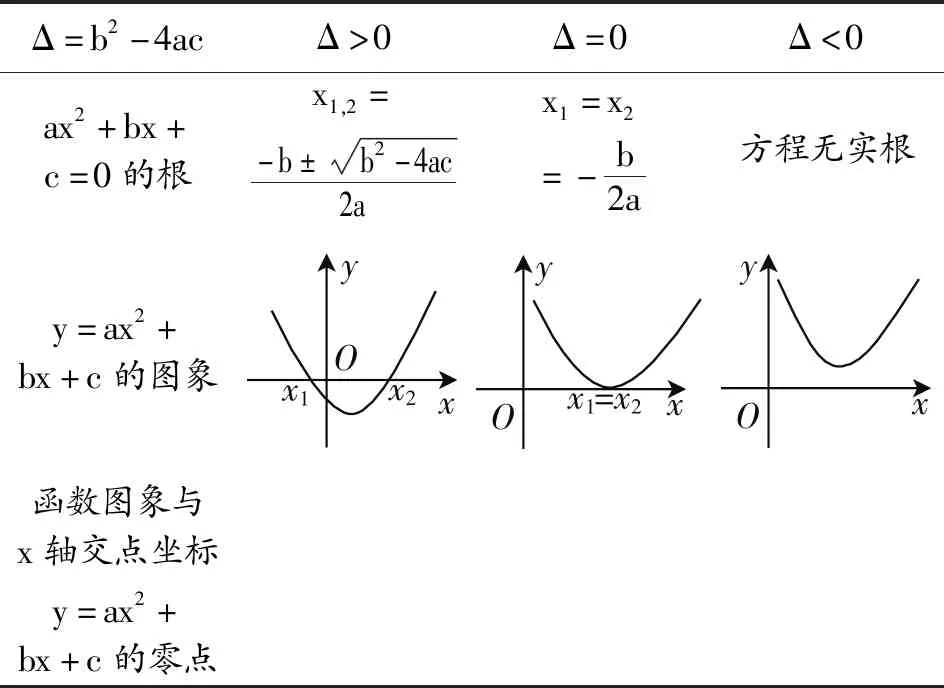
表1 一元二次方程与对应函数的关系
注:a>0.
师:各小组表格都已经填写好了,现在请结合表格内容归纳总结,一般一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系.
生6:一元二次方程ax2+bx+c=0(a≠0)的实数根就是二次函数y=ax2+bx+c(a≠0)的函数值y=0时自变量x的值,也就是二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标.
师:很好!一般地,把使函数y=f(x)的值为0的实数x称函数y=f(x)的零点,即方程f(x)=0的实数解叫做函数y=f(x)的零点.
设计意图:为了便于观察、计算,教师设计了几个简单的一元二次方程,通过方程的根与对应函数图象与x轴交点坐标相对比,得出了一元二次方程的根即为相应的一元二次函数图象与x轴交点的横坐标.结论得出后,为了将其转化为一般规律,教师让学生联想一般方程,完成了从特殊到一般的转化.在此基础上给出函数零点定义也就使定义更加具体形象了,学生也更容易总结归纳三者的关系:方程f(x)=0有解⟺函数y=f(x)的图象与x轴有交点⟺函数y=f(x)有零点.这样让学生经历由根到交点再到零点的过程,有利于培养学生的逻辑思维能力.
2.3 借助转化,检验应用
教学片段3:
例1求证:二次函数y=2x2+3x-7有两个不同的零点.
证法1:(代数法)考察二次方程2x2+3x-7=0,因为Δ=32-4×2×(-7)=65>0,所以方程2x2+3x-7=0有两个不等的实数根.因此,二次函数y=2x2+3x-7有两个不同的零点.
证法2:(几何法)由f(x)=2x2+3x-7的二次项系数是2,可知抛物线的开口向上,且f(1)=2+3-7=-2<0,所以二次函数y=2x2+3x-7与x轴有两个交点.因此,二次函数y=2x2+3x-7有两个不同的零点.
例2判断函数f(x)=x2-2x-1在区间(2,3)内是否存在零点.
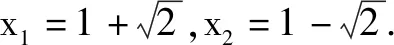
设计意图:在教学中,为了实现知识的内化,了例题环节.设置例1引导学生从不同角度思考零点问题,即代数法和几何法.对于例2,根据学情可知,在解决此类问题时多数学生习惯运用代数法来求解,教师可以顺势引导学生通过寻找“另外方法”为下面的教学内容作铺垫,让学生的思维在问题的引导下螺旋上升.
2.4 完善猜想,形成定理
教学片段4:
师:观察例2中函数f(x)=x2-2x-1的图象,我们猜想出“若函数y=f(x)在区间(a,b)内有零点,则必有f(a)f(b)<0”.如果这样说你们认为成立吗?“若函数y=f(x)在区间[a,b]上有f(a)f(b)<0,则函数y=f(x)在区间(a,b)内一定有零点”呢?
设计意图:通过创设问题引发学生对定理成立条件的关注,从而为定理的引入及内化作好铺垫.在教学中,可继续引导学生联想特例来验证,这样学生更容易理解“不间断的曲线”这一限定条件.接下来还可以提出问题①在什么条件下,可以使函数y=f(x)有唯一零点?②为什么题设中是闭区间[a,b],而结论中是开区间(a,b)?这样,通过仔细推敲和挖掘,让学生对定理的理解更加细致、全面,为后面的应用奠定坚实基础.
3 教学反思
本节课通过前期的铺垫,利用“函数与方程”“数形结合”等重要数学思想方法引发了学生对“函数零点”的思考,从而将方程的根、图象与x轴的交点、函数零点紧密相连,实现了代数与几何之间的转化.接下来又围绕“函数零点定理”经历了一次探究之旅,从观察、发现、猜想、推理、验证、应用等环节突破了重难点,发现了问题的本质,最终形成了定理.数学定理本是抽象的,为了提升教学的有效性,发展学生的数学思维,在教学中需要多从学生的认识角度去思考问题,通过创设有价值的问题引导学生在知识的梳理、归纳、总结等数学活动中建立完整的知识体系,进而提升解决问题的能力.
总之,要发挥课堂教学价值,离不开教师精心的预设.只有精心预设才能使知识向正方向迁移,从而揭示问题的本质,提炼出有价值的数学方法,最终形成解题能力和学习能力,提高数学核心素养.

