基于核心素养的高中数学模块单元教学设计
安徽省临泉第二中学
李海燕
在高中数学中,广大教师将教学内容组织的最小基本单元称为模块.从模块的角度出发进行教学,有利于教师对现有教材按照学情或教学计划进行整合,可以有效地帮助学生提高学习效率,构建符合学生需求的知识体系.
1 模块单元设计基本要求和指导思想
模块单元设计想要取得较好的预期教学效果,需要教师加深对教材的理解,明确教学目标,理清整个教材的知识安排思路.单元设计对于最终教学效果和学生知识掌握程度都有着重要作用.因此,教师在进行模块单元设计时,首先要认真分析单元知识在整个模块知识中的地位,以及与前后单元知识的联系和作用;然后,对该单元的教材、学情、课程标准、内容、知识态度目标等进行认真分析;最后,基于上述详细全面的分析,着手进行设计,并且要不断结合实践反馈进行调整.
模块单元设计的指导思想:第一,在高中数学课程标准思想的指导下,使用符合教学内容的教学手段和方法设计合适的教学方案,不断完成教学优化.第二,教学设计过程中要把握目标引导、程序合理、完整无遗漏、符合高中认知特点等原则.第三,要随时关注教材变化和课标要求,从整体高度设计好模块单元.要及时引入新的信息技术,从而提高高中数学课堂对学生的吸引力.
2 数学核心素养的内涵
数学核心素养是基于学生所处的阶段教材,对学生的综合能力提出新的要求.传统数学学科对学生的要求更多停留在学生的解题能力和方法上.但是数学核心素养要求学生在掌握上述要求基础上还要能够理解掌握其中的原理,提升自己的数学能力;注重学生获取知识、转换知识的能力,最终能够提升学生逻辑思维等能力,满足当今时代发展的要求.数学核心素养是基于当今时代要求提出的,具有一定的复杂性,也是对传统教学观念的改革,对一线教师提出了更高的要求;数学核心素养也同时具有多样性,学生所处阶段不同,核心素养的要求也会有所不同.
3 基于数学核心素养的高中数学模块单元设计案例
以高中数学新人教A版必修一第二章“一元二次函数、方程和不等式”为例,阐述模块单元教学设计的过程.
3.1 教材分析
本章位于新人教A版必修一第二章,第一章为集合知识,后续紧跟函数章节,可以起到承上启下的作用.主要内容要求:利用基本不等式求最值的关键是获得定值条件,解题时应对照已知和欲求的式子运用适当的“拆项、添项、配凑、变形”等方法创设应用基本不等式的条件.从方程角度认识不等式,体会一元二次方程、一元二次不等式的联系性.已知一元二次不等式的解集,能分析出原方程的根,画出二次函数图象,重点培养学生逆向思维能力.从函数角度认识不等式,体会二次函数、一元二次不等式关系的整体性.体会一元二次不等式恒成立问题与二次函数图象的结合问题,重点培养数形结合能力.
3.2 学情分析
高一的学生在初中一年级学习了一元一次方程,初中二年级学习了不等式,初中三年级学习了二次函数和一元二次方程,有了方程、不等式和函数的基本知识,基本概念已经形成,基本的数学思想有待建构,例如数形结合思想、转化思想、分类讨论思想等.高一学生学习自主能力较强,学习倾向于被动接受.
3.3 教学目标分析
(1)会用基本不等式解决常见的最值问题.
(2)利用二次函数、方程和不等式的关系解决一元二次不等式的有关问题,从而进一步体会用函数观点统一方程和不等式的数学思想.
3.4 整体教学设计思路
(1)需要认真思考不等式、函数两小节的讲授顺序.想要解决这个问题,需要厘清不等式和函数之间的关系.一元不等式都可以转化为f(x)小于或者大于0,也就是函数曲线在x轴上方或下方时对应的x的集合.先讲授不等式可以更好地帮助学生理解函数相关知识.
(2)需要思考本章内容和前后知识的关系在哪里?前面的集合知识如何与现在要设计的教学内容联系起来,应该如何引入,可以让学生快速回忆起之前所学习的集合知识.
(3)整体把握不等式和函数的教学,教师要基于学情分析选择载体,哪些载体更有利于学生掌握知识.例如直角坐标系等.
3.5 教学实施过程
(1)基本不等式的综合应用.
案例1已知x>0,y>0,2x+3y=1,求xy的最大值.
师生活动:学生独立思考,尽可能地提出解决问题的方法.
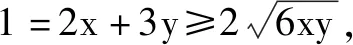
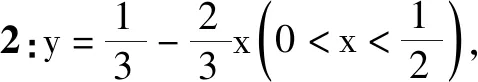
设计意图:从问题出发,引导学生进行一题多解,拓展思维.多数学生会用解法1来求解,其实xy表面为二元,实则可化归为一元,利用基本不等式或者二次函数都可以解决.提醒学生注意变量的取值范围.
(2)从方程角度认识不等式,体会一元二次方程和一元二次不等式的联系.
案例2已知一元二次不等式的解集为{x|-1 师生活动:学生在教师引导下解决问题,构造一元二次不等式时,需要考虑二次项系数的正负. 解:a(x+1)(x-2)<0(a>0);不唯一. 设计意图:由一元二次不等式的解集找出原不等式,这种开放式问题,既可以考查不等式的解与方程的根之间的关系,也有利于培养学生的逆向思维能力. 追问:已知一元二次不等式ax2+bx+1>0的解集为{x|-2 (3)从函数角度认识不等式,体会二次函数、一元二次不等式关系的整体性. 案例3若关于x的二次不等式ax2+(a-1)·x+a-1<0的解集为R,求a的取值范围. 师生活动:原不等式解集为R,即对一切实数x不等式都成立,故y=ax2+(a-1)x+a-1的图象开口向下,而且与x轴无交点,将其反应在数量关系上. 设计意图:突出等价转化思想. 从笔者目前所观察的高中数学教学流程而言,大部分一线教师对单元设计的概念并不是十分清晰,仍然简单地认为单元设计就是按照教材所规划的单元进行授课,缺乏对该种设计的正确认知,因此无法真正发挥模块单元设计的优势. 笔者认为,出现该种情况的根本原因是教师对模块单元教学设计不够理解,不能从数学核心素养角度联系实际教学进行思考,认知的片面性导致模块单元教学设计无法发挥其实效. 高中数学模块单元设计涉及到的知识点较多且复杂,在整个设计过程中需要遵循一定的规律安排,并且需要结合学情设置不同的三维目标.但是从目前的实践而言,许多教师在设计方法上没有明确的理论依据,与新课标及教学大纲要求有一定差距,并且部分教师自我要求较低,长时间没有更新自己的教学方法,导致模块教学设计对学生核心素养的提升较少. 针对此问题的对策如下:模块单元设计之前,在学科教研组内从提升学生核心素养角度开展讨论,认清学情,确定教学三维目标以及该单元在整个学科中所处的地位.其次,教师要紧跟时代步伐,主动学习,将新的合适的教学方法适时融入课堂教学当中.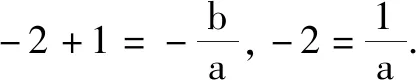
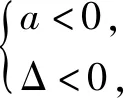

4 基于数学核心素养的高中数学模块单元设计存在的问题及对策

