MP-MMC驱动六相永磁同步风力发电机分数阶PID控制研究
姚钢,李华荣,周荔丹,曹祖加,王杰,黄孙华
(1.上海电力大学 电气工程学院,上海 200090;2.上海交通大学 电子信息与电气工程学院,上海 200240;3.广东电网有限责任公司茂名茂南供电局,广东 茂名 525000)
0 引 言
随着可再生能源的发展,海上风力发电市场逐步走向成熟。国内外对于清洁能源的需求不断增加,加速了海上风电的开发进程。海上风电机组的发展朝向深远海(一般认为离岸距离超过100 km、水深超过50 m)[1]、大容量以及高稳定性演变,机组变流器随着发电机容量的提升向由模块化变流器形成的多相化系统发展[2]。发展远距离大规模化的风电场,实现大功率发电机组高压直流并网成为现阶段研究热点[3-6]。
目前,风电系统中常采用双馈感应发电机和永磁同步发电机(permanent magnet synchronous generator,PMSG)。与双馈感应发电机相比,永磁同步发电机具有无需励磁电流驱动的优点,从而提高了工作效率,增强了系统的稳定性和可靠性[7]。此外,有相关学者将多相电机作为海上风电的未来的一个研究方向[8]。相对于三相发电机而言,多相电机中定子磁动势谐波含量更低,它可以提供更低的转矩脉动,更好的工作效率和功率密度。系统容错能力与稳定性较强。多相永磁同步电机将会在大规模海上风电系统中发挥重要的作用[9]。
模块化多电平变流器(modular multilevel converter,MMC)模块化程度高及扩展性强。它可以提供较高的输出电压和较少的谐波含量,并降低涡流损耗,有利于完成电压和功率的能量交换。在中高压直流输电的应用中,发展优势显著[10-13]。
对于大容量海上风电机组高压直流并网系统的研究,如文献[11]中基于多相永磁同步发电机(multiphase permanent magnet synchronous generator,MP-PMSG)机组构建的柔性直流海上风电场示意图所示。其中MMC驱动MP-PMSG风力发电部分,其采用PID控制器对转速环、电流环、谐波以及MMC进行控制。但该控制器难以满足系统快速响应、控制精度高、谐波含量低、直流汇集电压稳定等要求,尤其是对于高度模块化的MMC存在子模块电容电压不平衡、谐波含量较高和桥臂间环流较大等问题上,PID控制器的控制性能好坏将影响整个控制系统稳定性。目前还未有海上风电机组大规模应用MMC的商业实例,但不少学者已对此展开了相应的研究[11-15]。
分数阶微积分理论作为一种有效的数学工具,在控制领域得到了广泛的研究。相比于整数阶控制器,分数阶控制器增加了微积分阶次的控制参数,可灵活调节参数并可降低稳态误差,减小振荡幅度,提高响应速度,从而实现更加优异的控制性能[16-19]。目前,国外分数阶微积分理论研究状况要优于国内。在国外,分数阶理论在数学领域上得到开创与奠基[20-21]。除此之外,还实现了分数阶理论在机器人控制领域的应用[22]。国内不管是在起步时间还是研究成果都要相对落后,但是国内的研究热度却丝毫不落下风[23-28]。主要集中在分数阶PID(fractional order PID,FOPID)控制器上,并且较为集中在分数阶PID参数整定和研究应用两方面。在参数整定方面,薛定宇教授根据分数阶动态受控对象所期望的相位裕量和其幅值裕量的指标来设计分数阶PID控制器,取得了较好的控制效果[23]。在FOPID控制器的应用方面,文献[24-25]针对永磁同步电机伺服系统高动态响应要求设计了FOPID控制器来提高系统的整体性能。上述所涉及的系统体现了分数阶理论对系统有较好的控制性能。目前在风电系统分数阶理论大多都用于对电动机的转速环的PI控制或PID控制,MMC的控制暂时还没有文献将分数阶微积分理论引入。
因此,本文将分数阶理论应用于PID控制器的MMC驱动电机控制系统,设计FOPID控制器,并在发电机转速环、发电机定子的d、q轴电流闭环控制侧、z1,z2子空间的谐波分量控制处以及MMC内部能量均分模块处应用。分数阶PID控制器相比整数阶PID控制器增加了两个控制自由度,即主要影响控制系统稳态性能的积分阶次λ和主要影响控制系统动态性能的微分阶次μ,使得分数阶PID控制器的设计更加灵活,控制器控制能力提升。通过控制器控制能力的提升进而提高系统转速环、电流环控制能力,减小MMC子模块电容电压波动和桥臂环流值,优化MMC输出电压波形,降低谐波干扰,最后达到提升系统整体的稳定性和可靠性目标。
1 分数阶PID控制
1.1 分数阶微积分的定义
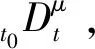
(1)

分数阶微积分的定义较多,目前主要定义有3种方式,即Grunwald-Letnikov (GL)定义、Riemann-Liouville(RL)定义、Caputo定义[20],本文所采用的分数阶微积分基于RL定义。对于α(0<α<1),f(t)是t的因果函数,即有当t<0时,f(t)=0,则RL分数阶积分和微分定义[29]分别为:
(2)
(3)
1.2 分数阶微积分的算法实现
分数阶微分方程的通常如下:
(4)
式(4)也可以用分数阶传递函数来描述,即
(5)
本文采用Oustaloup近似,给定近似频段的范围[ωb,ωh]及近似阶次N。根据分数阶微积分的阶次α,得对应的近似传递函数为
(6)
其中:
(7)
(8)
(9)
1.3 分数阶PID控制器
分数阶PID控制器的原理图如图1所示,其中:R(s)和E(s)为进行Laplace变换后的系统输入值与控制器输入值;U(s)和Y(s)为进行Laplace变换后的控制器输出值与系统输出值。

图1 分数阶PID控制器原理图Fig.1 Schematic diagram of FOPID controller
分数阶PID控制器在频域情况下的传递函数为
(10)
其中:Kp、Ki和Kd>0分别是控制器的比例、积分和微分增益系数;λ≥0和0≤μ≤1分别是控制器的积分和微分阶数。
与传统的PID控制器相比,分数阶PID控制器增加了控制参数λ和μ,使得其调节范围扩大。
1.4 参数λ和μ对控制性能的影响
分数阶控制系统之所以区别于整数阶控制系统,主要因为分数微积分算子sδ阶次的不同。Fourier数学变换理论为研究分数阶微积分算子sδ的频域性能奠定了理论基础。其中δ取值为参数λ和μ。
假设B(s)=sδ,δ≠0,则
B(jω)=(jω)δ,δ≠0,
(11)
由式(11)可以得到B(jω)的幅值裕度为
h=20lg|B(jω)|=20lg|jδωδ|=20δ|ωδ|。
(12)
其相角裕度:
(13)

整数阶PID控制器中的微分环节其相角超前90°,这样可以增加控制系统的阻尼度,来提高整个系统的动态特性;但是对于许多控制系统来说,90°的相角超前很多时候并不能满足系统的阻尼度,同样也不能达到很高的动态性能。通过对分数阶微分算子的频域性能分析可得,分数阶PID控制器微分环节的超前角度是可以通过微分的阶次μ来调节。通过μ值的选取可使超前相角在0~180°之间变换,这样便能满足许多控制在不同条件下的动态性能的需要。
同理,整数阶PID控制器中的积分环节其相角滞后90°,这样可以有利于控制系统稳态性能,但不是积分环节越大越好,因为相应的增大积分环节会降低控制系统的动态性能。可知分数阶PID控制器积分环节比整数阶PID控制器的积分环节增加了可以随意调节的阶次λ。这样就使积分环节的滞后角度可以灵活的在0~180°之间变换。这样就能够对控制器的积分环节进行微调解决控制系统动态性能和稳态性能之间的平衡矛盾。
2 系统模型
2.1 六相发电机数学建模
本文采用Y移30°结构的双三相永磁同步发电机。为简化分析,假设发电机定子绕组分布均匀,各绕组的电阻相等。同时,忽略磁路饱和及涡流损耗[11]。采用矢量空间解耦方法,得到定子电压方程为
(14)
式中Rs为定子电阻矩阵。相电压us,相电流is和磁链ψs分别为:
(15)
(16)
(17)
六相发电机的磁链,转矩以及运动方程为
ψs=Lsis+ψr×Φ(θ);
(18)
(19)
(20)
式中:ψr为主磁链幅值;Ls为定子电感矩阵;Te和TL分别为电磁转矩和输入转矩;np是极对数;J为转动惯量;θ为转子位置角;Φ(θ)为磁链系数矩阵。另外
(21)

(22)
其中:I6为6阶单位矩阵;Laal为定子绕组漏电感;Lms为定子励磁电感;
利用VSD坐标变换,将发电机相电压与相电流变换到旋转的垂直坐标系中,可以将PMSM的各变量分别映射到三个彼此正交的子空间,即d-q子空间,z1-z2子空间和零序o1-o2子空间,变换矩阵前两行对应d-q子空间,电机变量中的基波分量和12k±1(k=1,2,3,…)次谐波分量都被映射到该子空间上,且参与电机的机电能转换;变换矩阵中间两行对应z1-z2子空间,6k±1(k=1,3,5,…)次谐波分量都被映射到该子空间上,且不参与电机的机电能量转换;变换矩阵最后两行对应零序子空间,6k±3(k=1,3,5,…)次谐波分量都被映射到该子空间上,且不参与电机的机电能量转换,属于零序分量。其中变换阵为
(23)
其中:
B11=
B12=
将式(23)代入到式(15)、式(18)和式(19)中,忽略零序子空间谐波可以得到旋转坐标系下,发电机的数学模型为
(24)
其中:O为二阶0矩阵;
发电机的电磁转矩方程为
Te=3np[(Ld-Lq)idiq+iqψf]。
(25)
2.2 PMSG-MMC数学模型
六相永磁同步发电机和模块化多电平变流器(MMC)构成的系统拓扑图如2所示,图中n=4。MMC由十二个结构相同的桥臂构成。发电机连接在每相的中点,即上下桥臂之间。
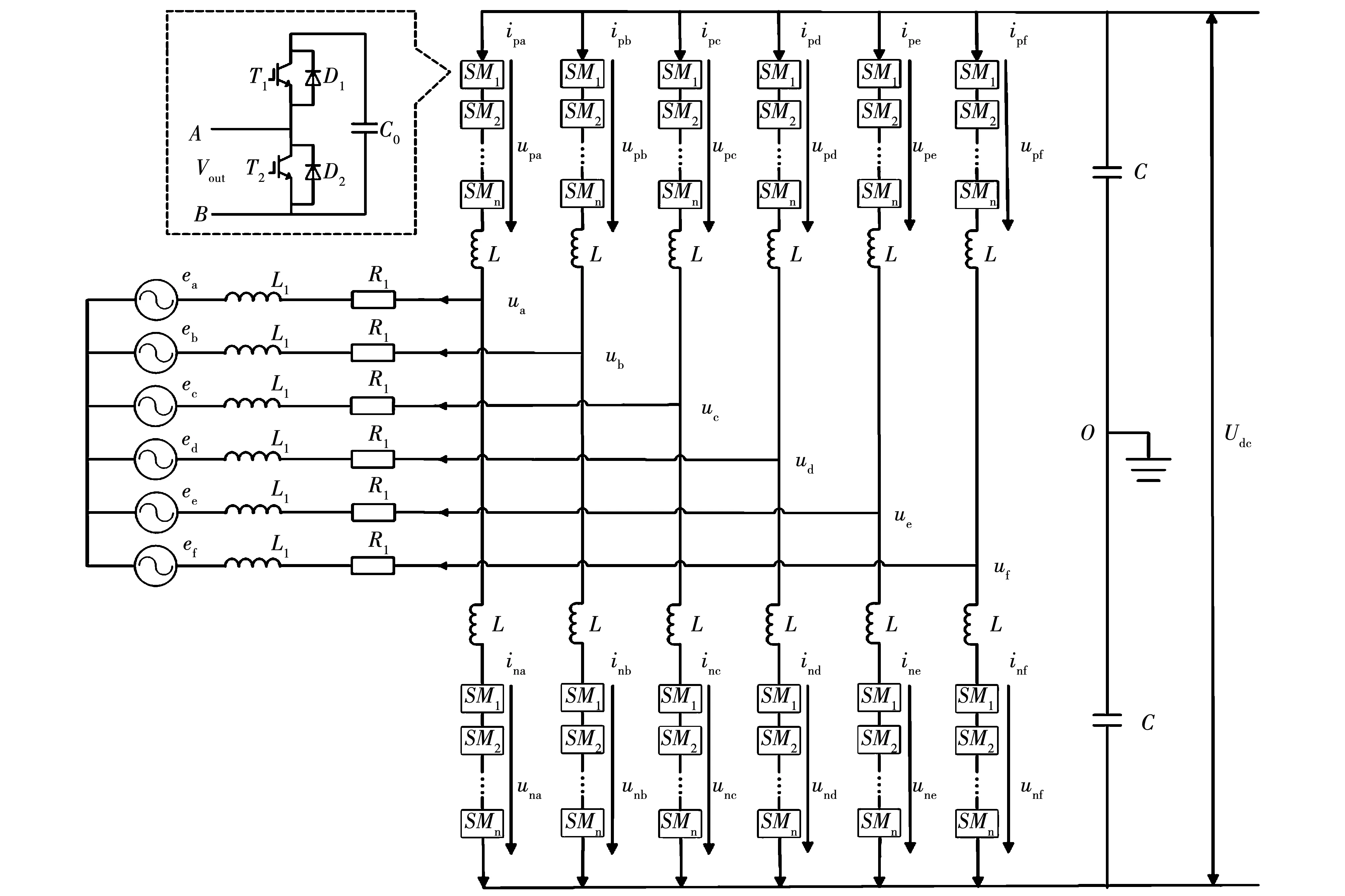
图2 六相PMSG-MMC系统拓扑Fig.2 Six-phase PMSG-MMC system topology
MMC的每个桥臂由数目相同的子模块和电感组成。本文系统中MMC子模块采用半桥结构类型,每个子模块由两个IGBT和电容构成。Rl和Ll为线路上的电阻和等值电感;em(m=a,b,c,d,e,f)为发电机m相感应电动势;Udc为MMC直流侧输出电压;Upm和Unm为MMC的m相上桥臂电压和下桥臂电压;L为桥臂电感;ipm和inm为MMC的m相上桥臂电流和下桥臂电流。
根据电路中的基尔霍夫电压定律,可得到MMC的m相上下桥臂电压upm、unm与交流侧电压ux之间关系为:
(26)
(27)
(28)
(29)
其中:ix为交流侧电流;icir为MMC内部环流,有
(30)
基于式(26)~式(30),可得六相永磁同步发电机和MMC所组成的系统等效电压关系式:
(31)
式中:Rl=RlI6,I6为6阶单位矩阵;us为MMC交流侧等效输出的6阶电压矩阵;Leq为等效电感矩阵,这里:
(32)
(33)
Ll=LsI6。
(34)
2.3 系统控制策略
由发电机和MMC组成的系统控制拓扑图如图3所示。
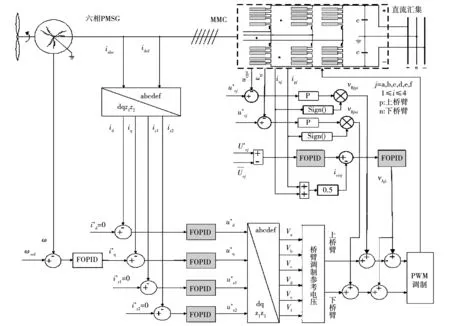
图3 六相PMSG-MMC系统控制拓扑图Fig.3 Six-phase PMSG-MMC system control topology
根据式(31)和分数阶PID的控制理论,可以得到发电机侧的控制策略如下:
(35)
z1,z2子空间的谐波分量控制策略为
(36)
发电机转速环的控制策略为式(25)和下式:
(37)

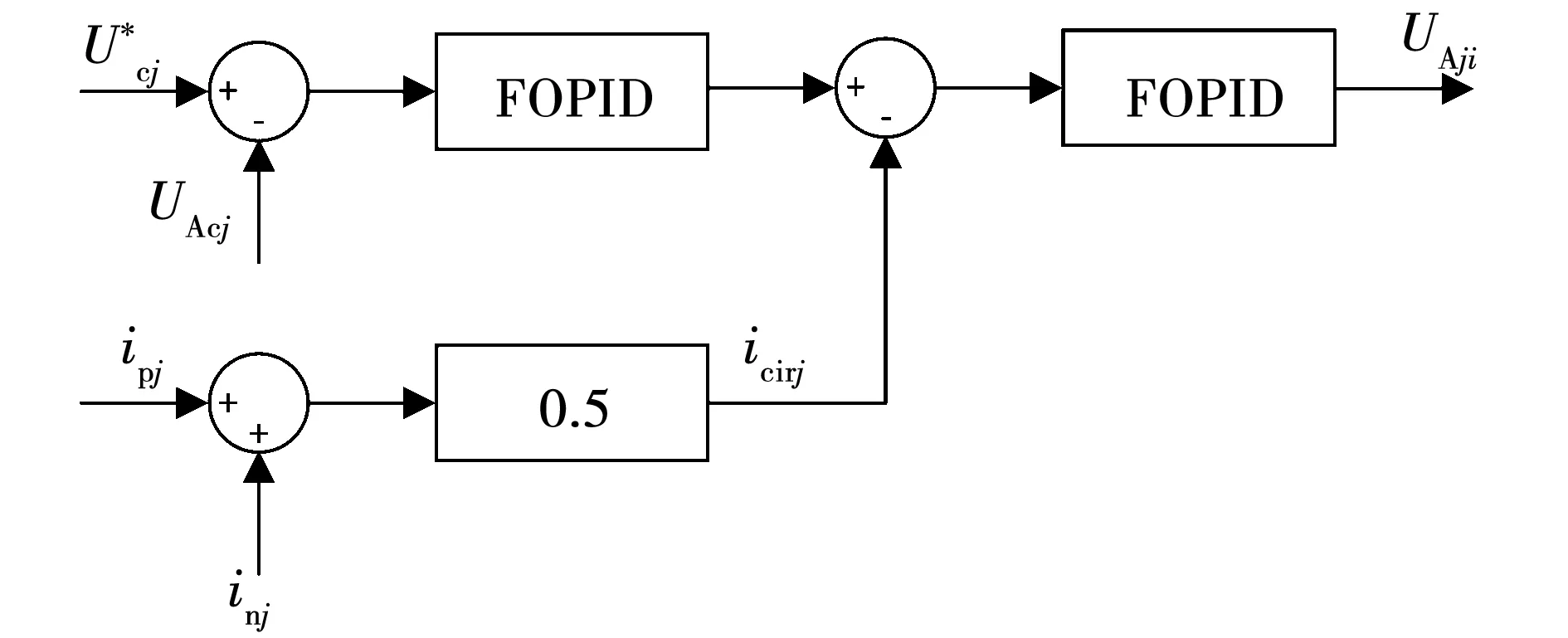
图4 MMC能量均分控制原理Fig.4 MMC energy averaging control topology diagram
MMC能量均分控制策略如下:
(38)
其中
(39)
3 仿真分析
为验证所提分数阶PID的优化控制性能,利用MATLAB/Simulink软件搭建了六相PMSG-MMC的系统仿真模型,并在发电机转速侧,发电机定子的d、q轴电流闭环控制侧以及MMC内部能量均分模块处,z1和z2子空间的谐波分量控制处引入分数阶PID控制器。首先给出一组整数阶PID参数,该组参数是对每个整数阶PID控制器局部最优后再在整个系统中寻优得到的参数;在此基础上为保证比较的公平性,令增益系数Kp、Ki和Kd不变,通过对微积分阶次λ,μ参数局部寻优和整体寻优给出另一组FOPID参数来比较两个控制器的控制性能。其中,系统参数如表1和表2所示。
为模拟六相PMSG-MMC系统的真实运行状态,以及验证分数阶PID的优化控制策略,在忽略风速因素影响的情况下,分别对六相PMSG-MMC系统在恒转矩和变转矩运行情况下进行了模拟仿真。

表1 PMSG仿真模型参数Table 1 Parameters of PMSG simulation model

表2 MMC仿真参数Table 2 Parameters of MMC simulation model
下述所分析系统恒转矩运行与变转矩运行的发电机输出电压、输出电流均为6相的,MMC子模块电容电压波形图、桥臂环流波形图均为以a相桥臂为例,并且其中的MMC子模块电容电压FFT分析图是以a相下桥臂最后一个子模块电容为例分析的。
3.1 恒转矩运行状态仿真
为验证MP-MMC系统在恒转矩下的稳定性,当发电机的输入转矩为-200 N·m,此时,当系统在恒转矩采用传统的PID控制策略时,在0.05~0.25 s运行时的结果如图5(a)~(e)所示,图5(f)、(g)为在0.1~0.25 s时MMC桥臂环流波形图与子模块电容电压FFT分析图,其中,电机的角速度稳定在300 rad/s;发电机的六相输出电压,幅值稳定在400 V;发电机六相输出电流,幅值稳定在16 A;MMC子模块电容电压波动范围为198.67 V到201.28 V;MMC桥臂环流波动范围为-8.51 A到1.72 A;MMC子模块电容电压FFT分析THD为1.39%。
当系统在恒转矩采用FOPID控制策略时,系统在0.05~0.25 s运行时的结果如图6(a)~(e)所示,图6(f)、(g)为在0.1~0.25 s时MMC桥臂环流波形图与子模块电容电压FFT分析图,电机的角速度为300 rad/s;发电机的六相输出电压幅值也稳定在400 V;六相输出电流幅值稳定在16 A;MMC子模块电容电压波动范围为199.08 V到200.92 V;MMC桥臂环流波动范围为-8.01 A到0.93 A;MMC子模块电容电压FFT分析THD为0.32%。
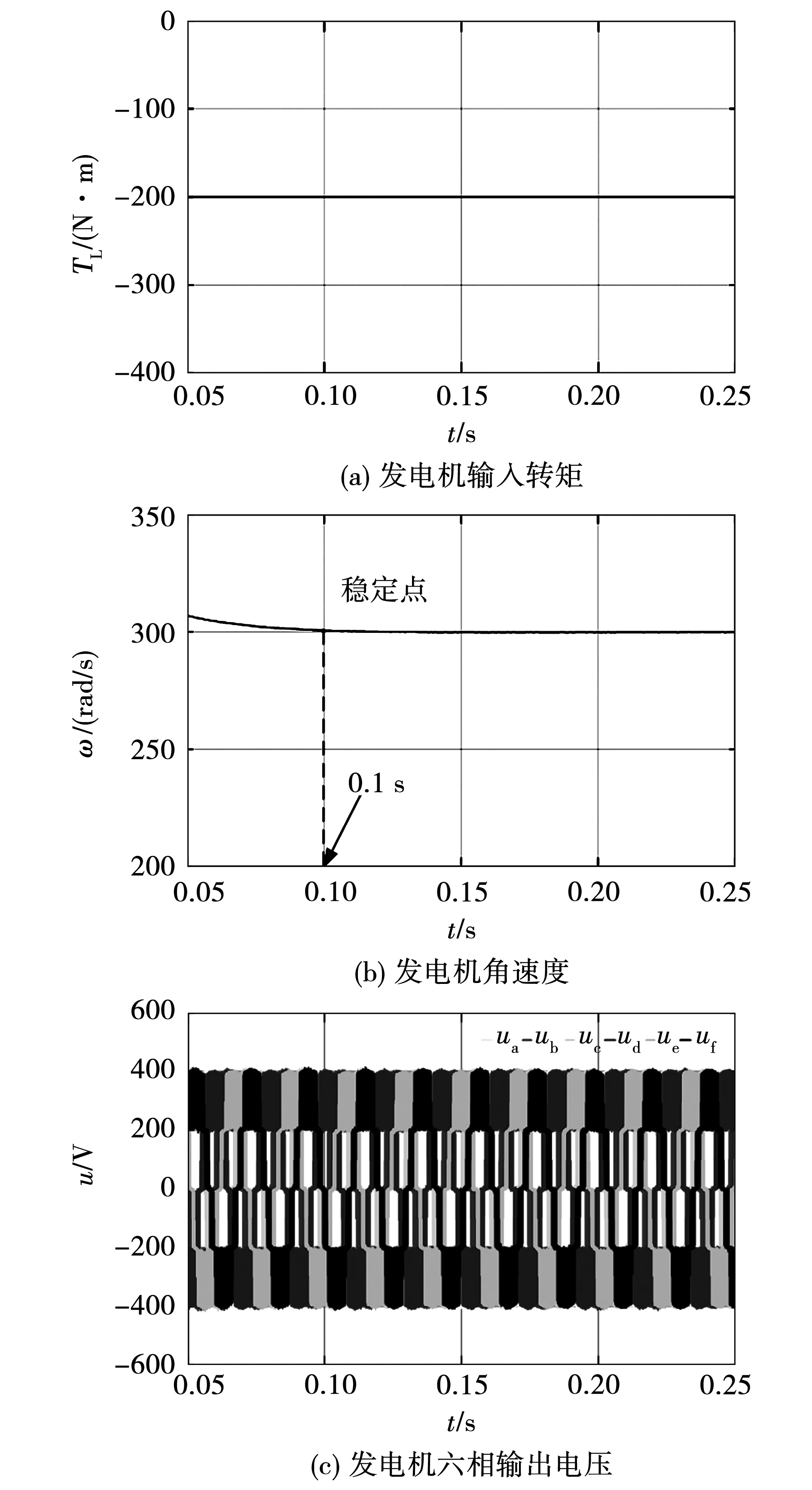


通过对比恒转矩情况下传统PID控制及改进FOPID控制可以发现,两者都可以实现MP-MMC的稳定运行,子模块电容电压值都在正常的波动范围之内。但是,当系统采用FOPID控制方法后,由于在发电机转速侧,发电机定子的d、q轴电流闭环控制侧部分使用FOPID控制器后,对比图5(b)和图6(b),发电机角速度提前0.025 s到达稳定,系统发电机的角速度动态性能更优。对比图5(e)和图6(e),子模块电容电压波动范围由原来的(198.67~201.28 V)降至(199.08~200.92 V),峰峰值降低0.77 V;对比图5(f)和图6(f),MMC桥臂环流波动范围由原来的(-8.51~1.72 A)降至(-8.01~0.93 A),峰峰值降低1.29 A;对比图5(g)和图6(g),MMC子模块电容电压THD由原来的1.39%降至0.32%。MMC内部能量均分使用FOPID控制器增加主要影响控制系统稳态性能的积分阶次 参数和主要影响控制系统动态性能的微分阶次 参数,这使得子模块电容电压幅值及其谐波畸变率降低,进而MMC输出的各个电平电压与标准电平电压差值减小,输出电压波形得到改善;同时使得MMC的桥臂环流峰峰值降低,环流波形得到改善,减少了无功功率的传输,控制性能更优。

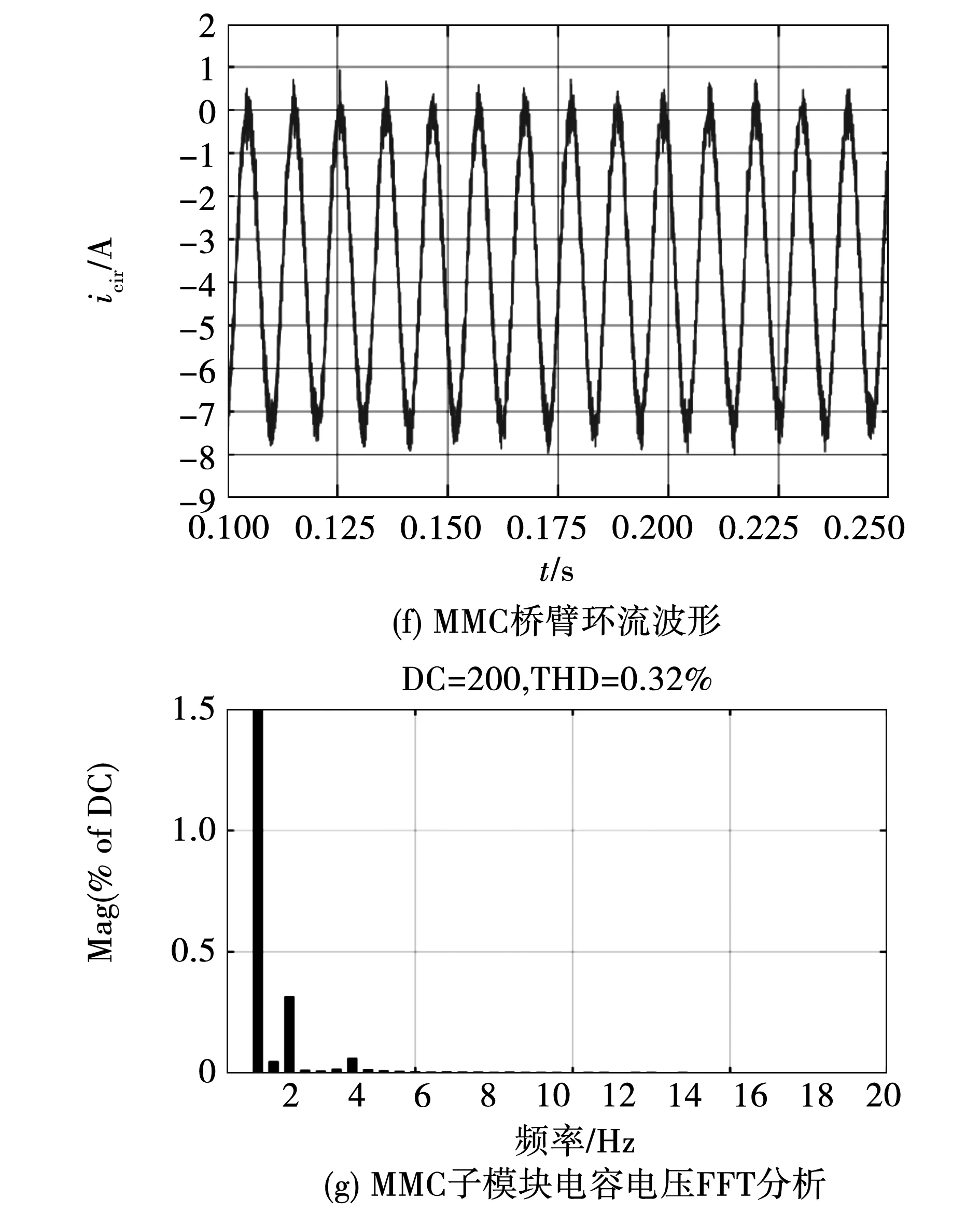
图6 恒定转矩时采用FOPID控制的系统仿真图Fig.6 Simulation diagram of FOPID control system with constant torque
3.2 变转矩运行状态仿真
为验证MP-MMC系统的鲁棒性,在0.35 s时,发电机的输入转矩发生阶跃突变,由-200变为-320 N·m。此时,采用传统PID控制时,系统在0.25~0.45 s运行时的结果如图7(a)~(e)所示,图7(f)为在0.3~0.45 s时MMC桥臂环流波形图,图7(g)为在0.41~0.45 s运行时的a相MMC子模块电容电压FFT分析图,由图7(a)可见,电机的角速度仍然可以维持在300 rad/s。发电机六相输出电流,幅值由稳定在15 A左右发生阶跃突变后稳定在26 A;发电机六相输出电流,幅值稳定在26 A左右。在0.41~0.45 s运行时,MMC子模块电容电压波动范围为198.21~201.81 V;MMC桥臂环流波动范围为-12.81~1.42 A;MMC子模块电容电压FFT分析为THD为2.22%。
当采用改进的FOPID控制策略时,系统在0.25~0.45 s运行时的结果如图8(a)~(e)所示,图8(f)为在0.3~0.45 s时MMC桥臂环流波形图,图8(g)为在0.41~0.45 s运行时的a相MMC子模块电容电压FFT分析图,电机的角速度稳定在300 rad/s;发电机的六相输出电压幅值也稳定在400 V;六相输出电流幅值由稳定在15 A左右发生阶跃突变后稳定在26 A左右;在0.41~0.45 s运行时,MMC子模块电容电压波动范围为198.41 V到201.55 V;MMC桥臂环流波动范围为-12.05 A到0.97 A;MMC子模块电容电压FFT分析为THD为0.62%。
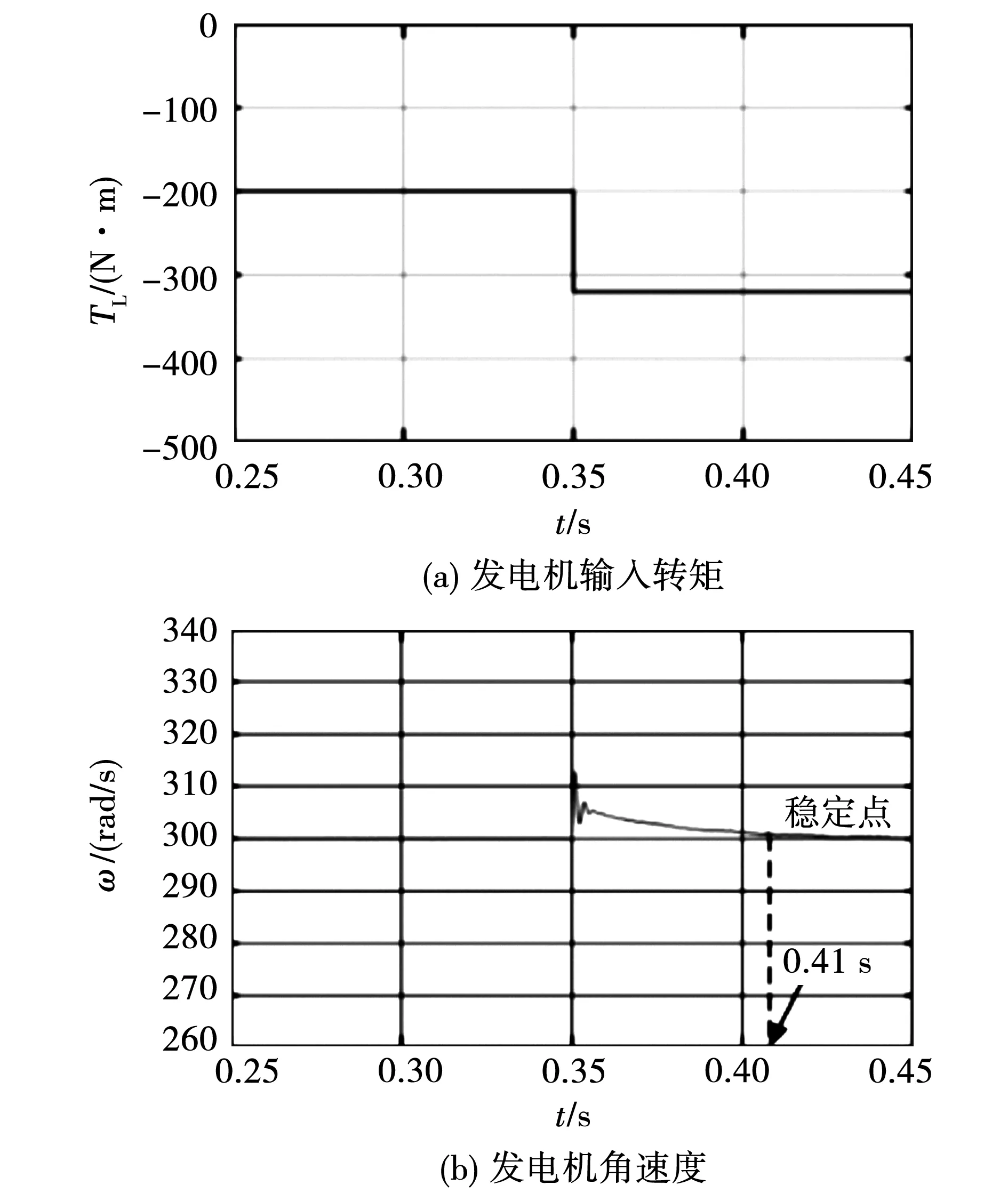


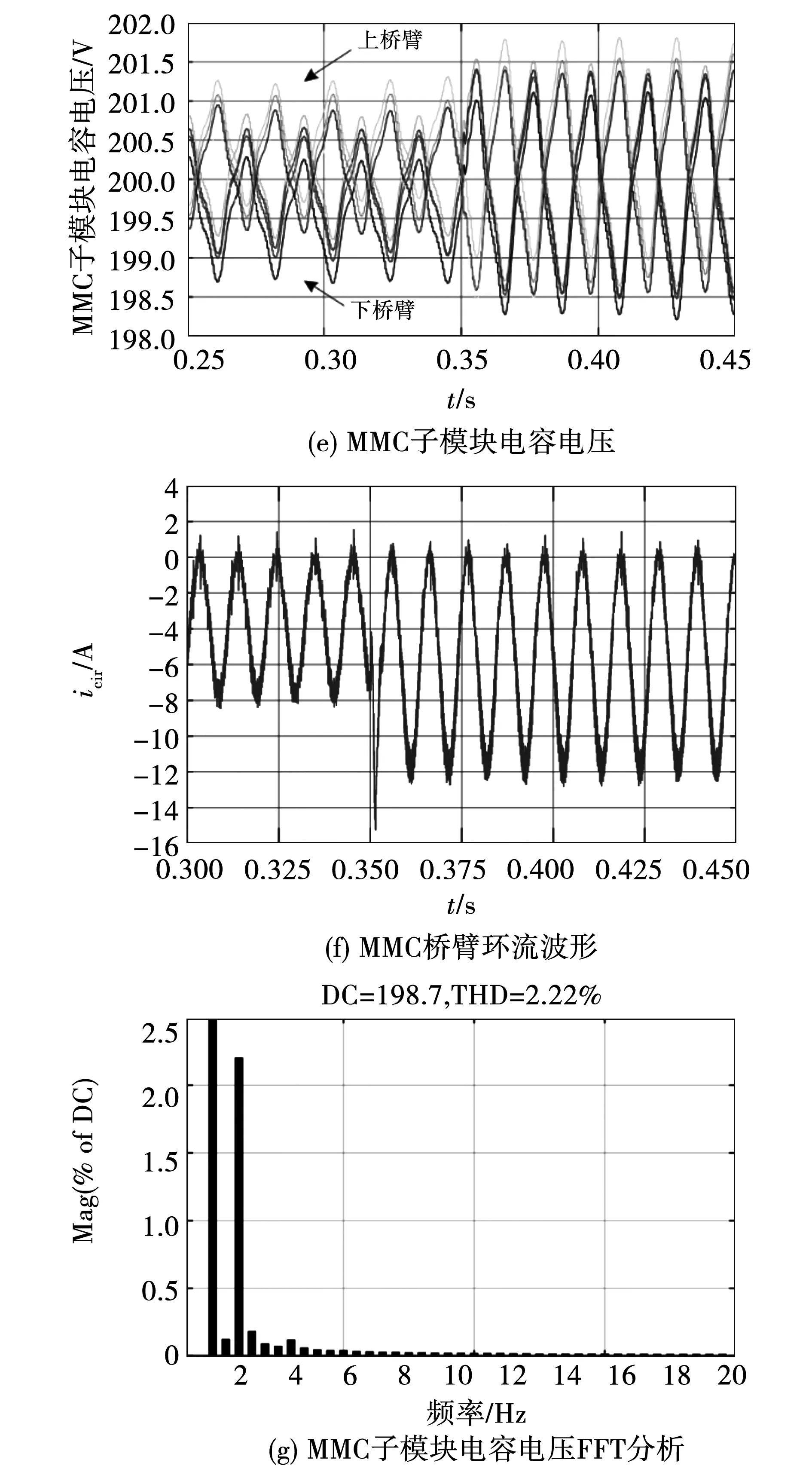
图7 变转矩时采用PID控制的系统仿真图Fig.7 System simulation diagram of PID control system with variable torque
与采用传统PID控制策略的MP-MMC系统相比,采用改进FOPID控制方法的系统拥有良好的鲁棒性,控制效果更加优异。由于在发电机转速侧,发电机定子的d、q轴电流闭环控制侧部分应用FOPID控制器后,对比图7(b)和图8(b),在变转矩运行后,发电机角速度会在0.38 s再次稳定,而使用整数阶PID控制策略时,发电机角速度会在0.41 s再次稳定,发电机角速度稳定会提前0.03 s,系统采用改进的FOPID控制策略时发电机的角速度动态性能更优;在MMC内部能量均分处以及z1和z2子空间的谐波分量控制处使用FOPID控制器使得在0.41~0.45 s期间,子模块电容电压波动范围由原来的(198.21~201.81 V)降至(198.41~201.55 V),峰峰值降低0.46 V;MMC桥臂环流波动范围由原来的(-12.81~1.42 A)降至(-12.05~0.97 A),峰峰值降低1.21 A;在0.41~0.45 s对MMC子模块电容电压FFT分析为THD由原来的2.22%降至0.62%。与上述恒转矩分析结果一致。

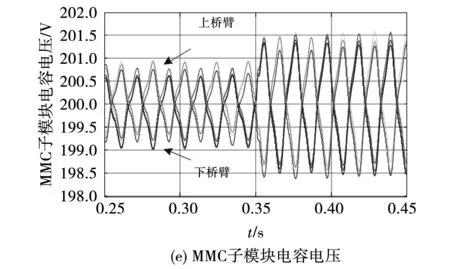
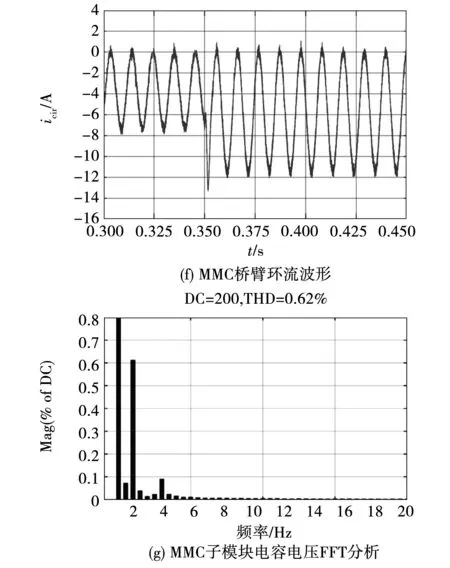
图8 变转矩时采用FOPID控制的系统仿真图Fig.8 System simulation diagram of FOPID control system with variable torque
4 实验验证
为了验证所提控制方法的有效性,本文利用双三相永磁同步电机,MP-MMC和RTU系统搭建在环半实物仿真进行验证。实验平台如图9所示,电机实验参数如表1所示,MP-MMC实验参数如表2所示。
由于示波器通道数目有限,因此采用2台示波器分别对a,b,c相和d,e,f进行观察。
当采用传统的PID控制策略时,系统运行稳定后,此时系统的运行结果如图10所示,通过示波器可以读出,电机六相相电流幅值为15.32 A,其中,a,b,c相相电流波形图如图10(a)所示,d,e,f相相电流波形图如图10(b);MMC中a相桥臂环流如图10(c)所示,波动峰峰值范围为-7.91~1.35 A。其局部波形图如图10(d)所示。
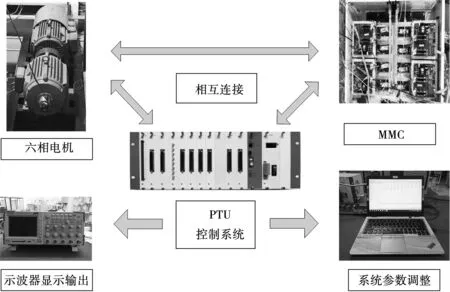
图9 实验平台Fig.9 Experimental system
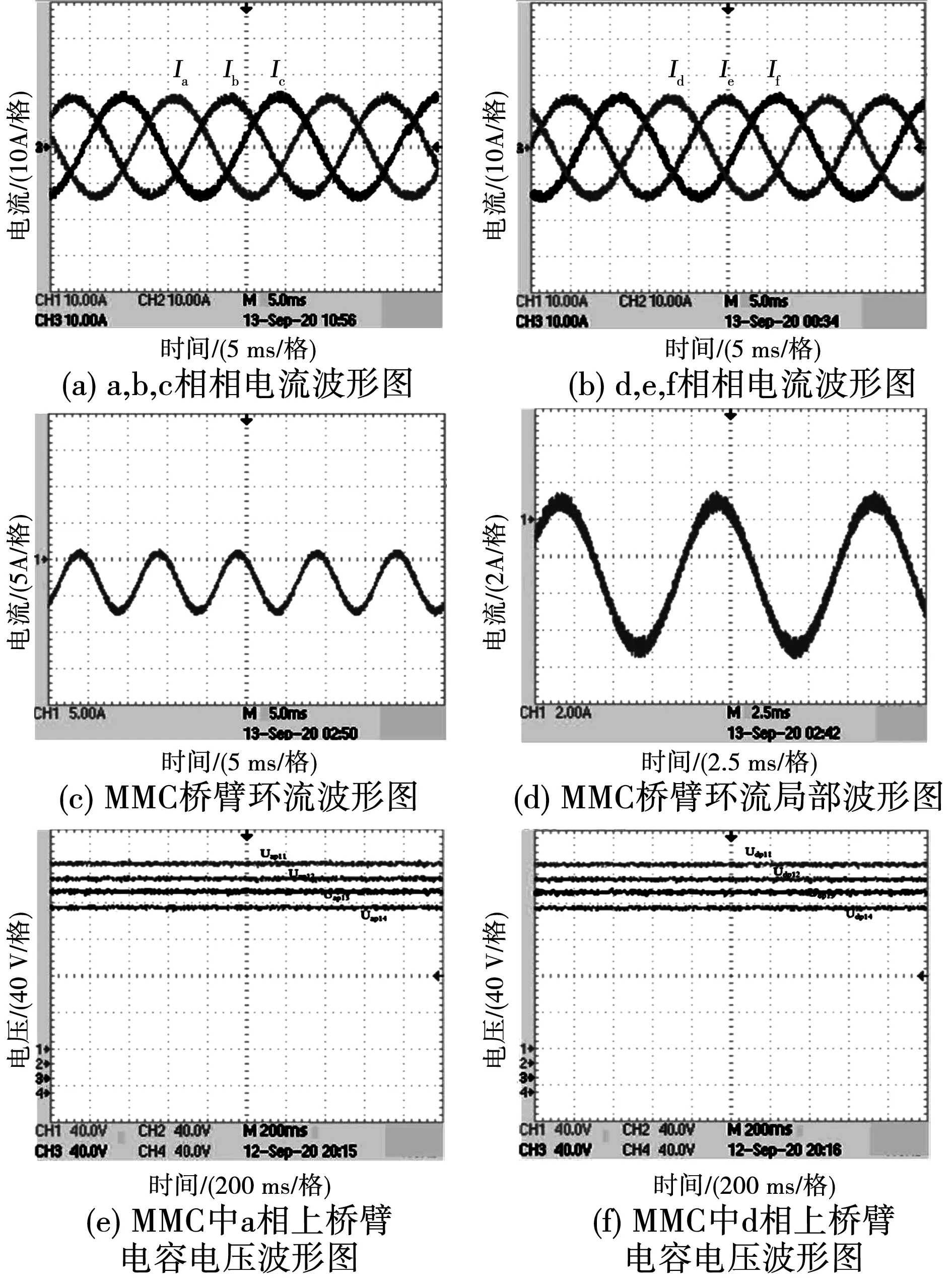
图10 采用PID控制的系统实验波形Fig.10 Experimental waveforms of PID control system
MMC中a相上桥臂子模块电容电压波形图及MMC中d相上桥臂子模块电容电压波形图如图10(e)和图10(f)所示。由示波器可读出,其中各子模块电容电压最大峰值Uap11、Uap12、Uap13、Uap14大小为别为201.2、201.1、200.9、200.6 V;Udp11、Udp12、Udp13、Udp14大小分别为201.1、201、200.8、200.7 V;最大峰值平均波动0.925 V,最大峰值波动率为0.462 5%。
当系统采用改进的FOPID控制策略时,系统运行稳定后,此时系统的运行结果如图11所示,且通过示波器可以读出,其输出电流幅值为15.13 A。与PID控制策略相比,MMC输出电流波形相对较好。
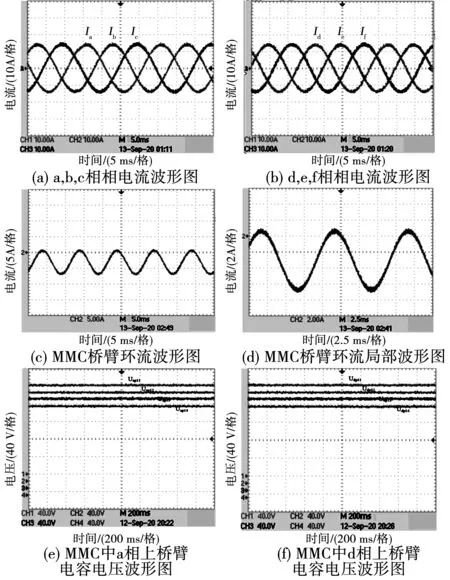
图11 采用FOPID控制的系统实验波形Fig.11 Experimental waveforms of FOPID control system
通过观察图11(a)中a,b,c相相电流波形,图11(b)中d,e,f相相电流波形图,图11(c)中MMC桥臂环流和图11(d)中MMC桥臂环流局部波形可以发现,由示波器可读MMC桥臂环流波动范围稳定在-7.42~1.12 A。幅值相对于PID控制时的桥臂环流(-7.91~1.35 A)峰峰值减小了0.72 A左右。图11(e)为MMC中a相上桥臂子模块电容电压波形图及图11(f)为MMC中d相上桥臂子模块电容电压波形图,示波器读出各子模块电容电压最大峰值Uap11、Uap12、Uap13、Uap14大小为别为200.8、200.7、200.6、200.4 V;Udp11、Udp12、Udp13、Udp14大小为别为200.7、200.6、200.5、200.3 V;最大峰值平均波动0.575 V,最大峰值波动率为0.287 5%。相对于PID控制器控制下a相各子模块电容电压最大峰值下降0.4、0.4、0.3、0.2 V;d相各子模块电容电压最大峰值下降0.4、0.4、0.3、0.4 V。加入的λ和μ可调节的参数使控制更为精确,在MMC内部能量均分处的FOPID控制器使得子模块电容电压幅值降低,进而MMC输出的各个电平电压与标准电平电压差值减小,输出电压波形得到改善;同时也使得MMC的桥臂环流峰值降低,环流波形得到改善,减少了无功功率的传输,控制器性能更优;上述相应的电流波形也等到改善。进一步提升了系统稳定性。与前面章节的理论分析一致。
5 结 论
本文针对多相模块化电平变流器驱动多相发电机,在Y移30度六相永磁同步发电机旋转坐标系下的数学模型基础上,引入了分数阶PID控制器。
通过仿真和实验对比在系统上应用FOPID控制器和应用整数阶PID控制器得到的结果:应用FOPID控制器的系统子模块电容电压幅值及其谐波畸变率降低,MMC的桥臂环流峰峰值降低以及发电机转速动态性能与稳态性能进一步改善,在恒转矩仿真中可得单臂子模块电容电压峰峰值降低0.77 V,峰峰值波动率减小0.385%,环流波动峰峰值降低1.29 A;子模块电容电压THD可降低1.07%;在变转矩仿真中FOPID控制器的系统能提前0.03 s到达稳定。证明了通过调节增加控制系统稳态性能的积分阶次λ参数和主要影响控制系统动态性能的微分阶次μ参数,可使得分数阶PID控制器的控制效果更佳。证明了分数阶理论应用于采用PID控制器控制MMC系统方法的优越性。

