永磁同步电机交直轴增量电感计算与测量研究
李巍,王浩淞,陈伟
(1.同济大学 电子与信息工程学院,上海 201804;2.上海新时达电气股份有限公司,上海 201801)
0 引 言
永磁同步电机具有结构紧凑、损耗小、效率高等显著优点,因而应用范围极为广泛,几乎遍布航空航天、国防、工农业生产和日常生活的各个领域[1]。随着永磁同步电机在各个领域的应用不断推广,对其控制性能也提出了更高的要求,而大多数先进控制算法是基于永磁同步电机精准的模型和参数实现的[2]。电感参数作为永磁同步电机模型中的重要参数,对电机的动态性能评估和高精度控制都非常关键。
电感反映了绕组在一定电流下产生磁链的能力,对于固定磁路且磁导率为恒值时,磁链与流过线圈的电流之间有正比关系。由于铁心部分的饱和效应,电机绕组的磁链与电流呈非线性关系,这就引出了增量电感的概念[3]。文献[4]提出了一种利用增量电感建立永磁同步电动机dq0转矩模型的方法,文献[5]阐述了永磁同步电机的增量电感用于电机故障诊断的原理,通过对比增量电感的两个峰值可以检测电机的静态偏心率。因此,对永磁同步电机的增量电感进行研究具有一定的实际价值。
随着电磁场数值计算技术的进步和广泛推广,采用有限元法计算电机电感参数较为准确,因此有限元法成为计算电机非线性电感参数的主要手段。目前大多数商业有限元软件可以选择计算三相绕组的视在电感和增量电感,并且有的软件可以通过脚本文件直接计算出交直轴电感。对于电机的铁磁材料来说,不同电流下铁磁材料的磁导率会发生变化,因此电感参数也随之变化。针对铁磁材料饱和效应引起的非线性电感的计算,可通过冻结磁导率法实现[6-7],也有部分研究采用了有限元法结合交直轴分解理论直接计算出永磁同步电机交直轴电感[8],这些方法能够较快地计算出永磁同步电机的交直轴电感,但是计算情况并未完全考虑到电机的实际工况。
永磁同步电机电感计算通常发生在电机设计或者优化设计的过程中,由于计算需要已知电机的具体设计参数。而对于工程应用端,并无法获取电机的具体设计参数,因此通常采用基于实验的电感参数辨识方法来获得交直轴电感。为了能够准确辨识出永磁同步电机的电感参数,国内外学者都开展了大量研究工作,并取得了很多优良的成果。现今的电感参数辨识方法大体可以分为两大类,即在线辨识和离线辨识。在线电感参数辨识比较常见的方法有最小二乘法、模型参考自适应法、扩展卡尔曼滤波法以及智能算法等[9-11],这些方法从不同的策略和算法上对参数进行辨识,能保证一定的辨识精度和跟踪性能,但在辨识过程中容易造成数据饱和,算法也较为复杂。离线电感参数辨识主要基于永磁同步电机的数学模型,在某些特定的条件下进行实验测量,再推导出交直轴电感,常用的方法有直流衰减法、交流静态法、矢量法等[12-14]。
本文以一台功率为5 kW的内置式永磁同步电机为分析对象,采用有限元法计算交直轴增量电感及其随电流的变化情况,分析在磁路不同饱和程度下交直轴增量电感的变化规律;为了进一步对比增量电感与视在电感的差异,同时对一台未充磁同型号电机进行相应的电感计算,较全面地阐明永磁同步电机交直轴的视在电感和增量电感的关系。最后,采用多种不同的离线方法对交直轴电感进行测量,并与相应的计算结果进行比较,验证理论和计算分析的正确性。
1 视在电感和增量电感
在理想的永磁同步电机的数学模型中,一般会假设铁心的磁导率为常值且绕组电感不变,但在实际电机中,由于铁磁材料的非线性,电感参数为变量,具体按照磁链和电流的关系又可分为视在电感和增量电感[15]。
视在电感的定义为电机静止状态下的电感,所以又称为静态电感,其大小等于磁路中电流产生的磁链与该电流的比值,如图1所示,若电机运行在点P处,OP的斜率即为P点视在电感,表达式为
(1)
增量电感一般用来描述电机的动态特性,所以也称为动态电感,其大小为工作点所在磁化曲线切线的斜率,如图所示运行点P处,曲线上P的斜率即为P点的增量电感,表达式为
(2)
式(1)、式(2)中:Lapp为视在电感;Linc为增量电感;ψ为电流为I时磁路中的磁链。
一般来说,铁磁材料的磁化特性曲线可以分成非饱和区和饱和区,当磁路在非饱和区时,两种电感的大小近似相等,即Lapp≈Linc,随着绕组电流的增加,磁路的工作点会从非饱和区进入饱和区,此时视在电感和增量电感的值均呈下降趋势,且明显增量电感下降得更快。
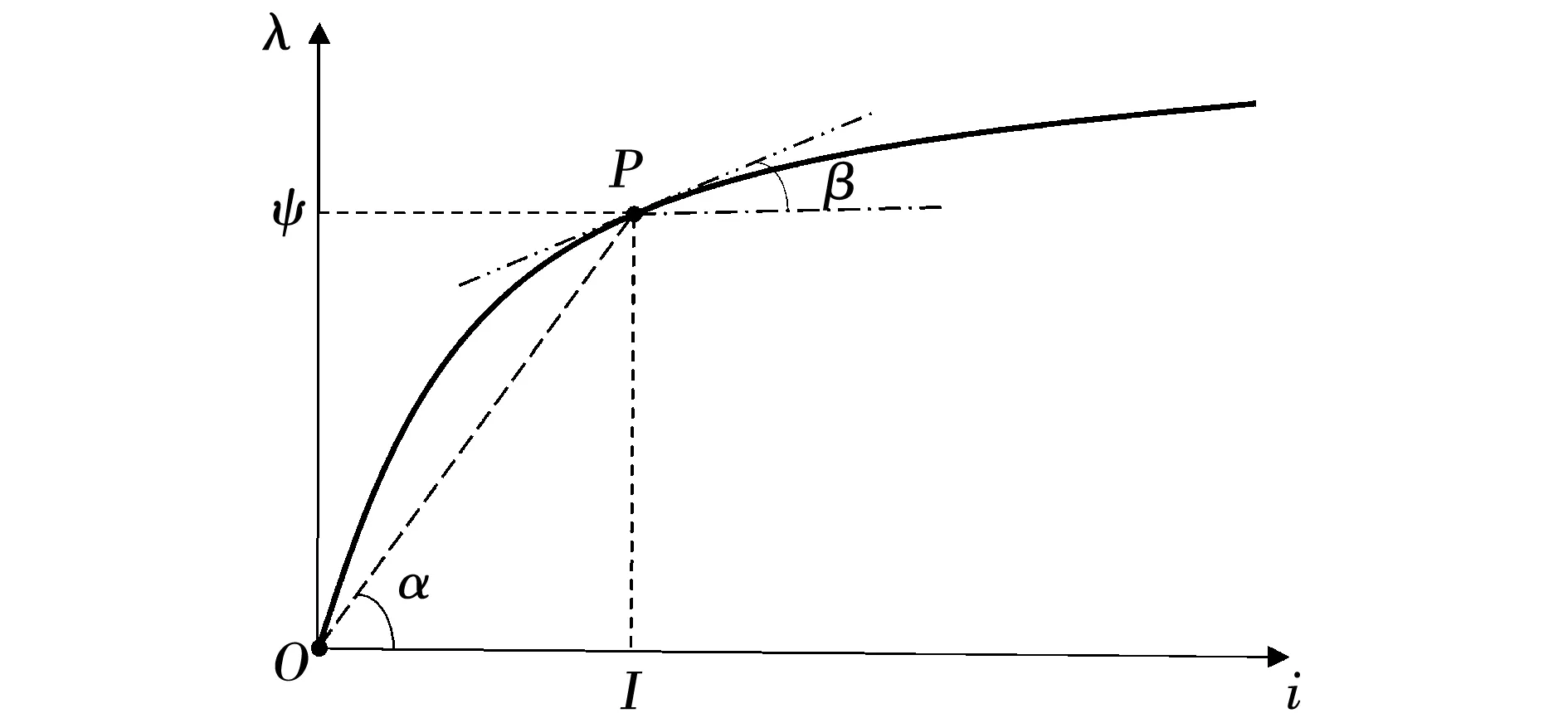
图1 绕组铁心磁化特性及工作点示意Fig.1 Magnetization characteristics of core and its operation point
根据法拉第电磁感应定律,电机绕组的电压方程为
(3)
可以看出,永磁同步电机数学模型中的电感均为增量电感,为了准确描述永磁同步电机的动态特性,准确地评估增量电感具有重要的意义。
2 基于有限元法的电感参数计算
2.1 计算原理
采用有限元法计算永磁同步电机在特定负载条件下的交直轴电感时,为了考虑齿槽的影响,通常采用瞬态场求解出转子旋转一个周期过程中的定子三相绕组的电感值,然后通过坐标变换得到交直轴电感值。在瞬态场每个步长的有限元计算完成后,每个单元在工作点处的磁导率被冻结,用于后续的电感参数计算。根据电感的定义,给定一个电流激励,计算在所冻结的磁导率和给定的电流激励条件下的磁链,便可求解出电感。冻结磁导率法在有限元计算电感中广泛应用[16]。
2.2 有限元建模
本文选用了一台内置式永磁同步电机作为计算对象,该电机有4对磁极,定子采用双层绕组,Y型连接,电机额定参数如表1所示。
根据电机的设计参数,在有限元软件中建立永磁同步电机的模型。定子槽型采用梨形槽,转子采用内嵌式永磁体,电机几何模型如图2所示。完成电机的几何建模后,再分别对电机的基本参数、材料属性、网格剖分、机械运动、边界条件和激励源等进行设置,即可对永磁同步电机的电感参数进行计算。
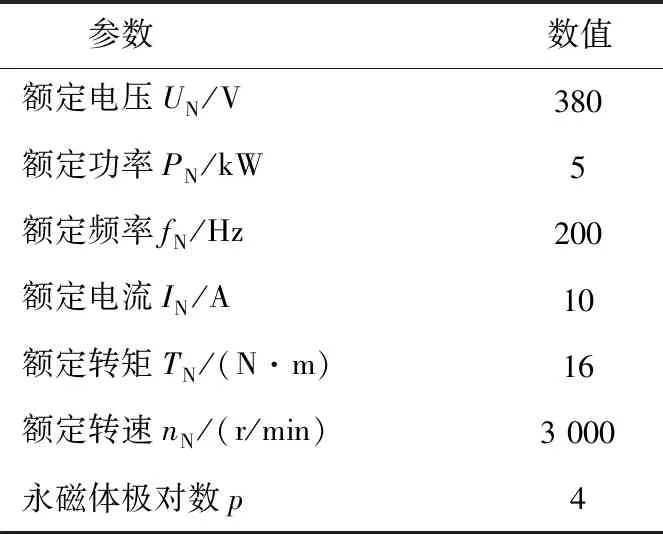
表1 永磁同步电机参数Table 1 Parameters of the PMSM
图2 电机几何模型图Fig.2 Geometric model of prototype motor
2.3 增量电感计算及分析
在常用的永磁同步电机控制方法中,如id=0控制、最大转矩电流比(MTPA)控制等,都是通过调节电流矢量实现的。本文通过调节电流矢量实现交直轴电感及其交叉饱和效应计算,通过改变电流矢量与直轴的夹角γ,可实现交直轴电流的调节,如图3所示。
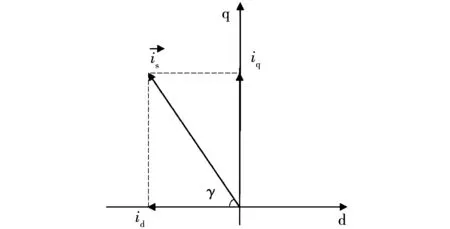
图3 dq坐标系下的电流矢量关系Fig.3 Relationship of current vector in dq coordinate system
定子绕组中通入如下三相对称的正弦交流电,当定子A相绕组轴线与直轴重合时,通过调节定子电流相位角φ即可调节定子电流矢量角γ:
(4)
式中:is为定子三相绕组一相的电流幅值;f为电机的同步频率。采用 “非功率形式不变”的坐标变换,可得交直轴电流为
(5)
其中:θ为转子位置的电角度,即直轴与A相绕组轴线的夹角,且有θ=ωt=2πft,代入式(4),联立式(5)可以求解得到is与交直轴电流id和iq满足以下关系式:
(6)
由式(6)可知,电流幅值is和相位角φ的关系与图1中电流矢量和矢量角γ的关系相一致,可以通过改变电流激励控制电流矢量在电机直轴和交轴上的分配。计算时设置电机转速n=3 000 r/min,设定is的变化范围为0~10 A,每隔1 A取一个计算点,使γ在0°到180°范围内变化,且每隔30°取一个计算点,因此共有70个电流幅值和相角的组合,交直轴增量电感的计算结果如图4所示。
从图4(a)可知,当矢量角γ=0°时,交轴电流iq=0,去磁性质的直轴电流削弱了永磁体产生的磁链,直轴磁路的饱和程度降低,因此直轴电感Ld会随着负载电流is的增大而增大,这与常规理论分析一致。当0°<γ<90°时,直轴电流和交轴电流同时存在,而Ld仍会随着is的增大而增大,可见在额定负载电流工况下,Ld主要由id的大小决定,与交轴磁路的饱和程度关系不大。当90°<γ<180°时,此时直轴电流为增磁性质,直轴磁路变得更加饱和,因此Ld随着负载的增大而减小。
从图4(b)可知,当矢量角γ=90°时,直轴电流id=0,只存在交轴电流iq,交轴电感Lq会随着负载电流is的增大而减小,这也与常规理论分析一致。但当γ较小时,Lq会随着is先增大后减小,且γ越小Lq的拐点越靠后,如图5所示,可见与直轴磁路相比,交轴磁路受交叉饱和的影响更加严重。
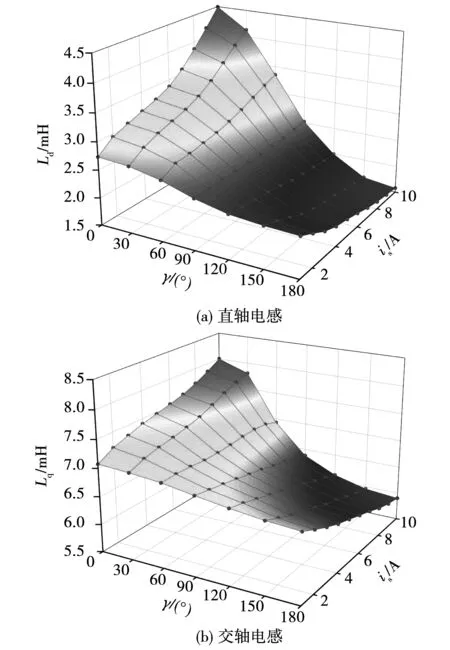
图4 交直轴增量电感随电流及矢量角的变化Fig.4 Variation of dq-axis incremental inductance with current and vector angle
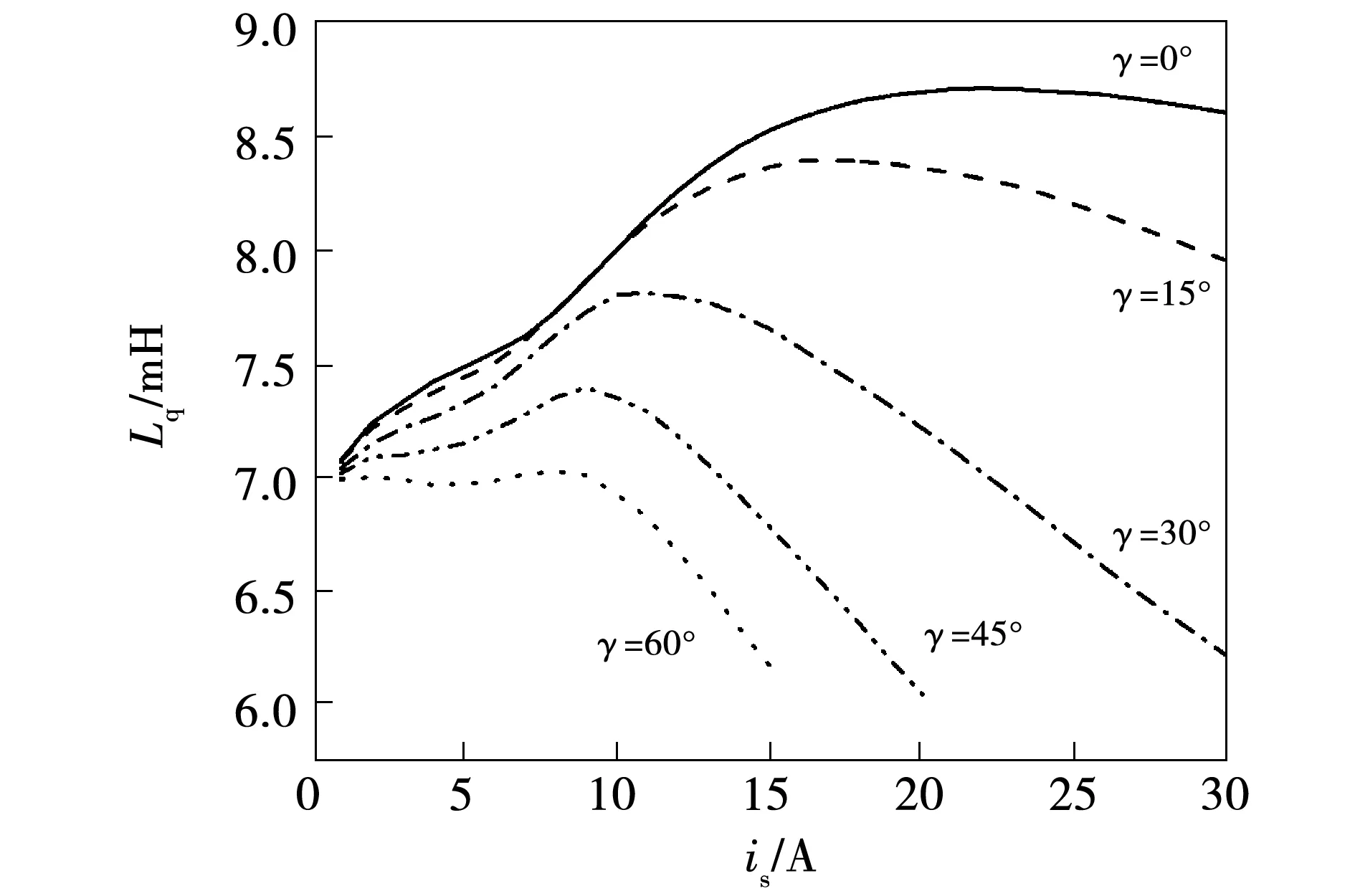
图5 不同矢量角下电流对交轴电感的影响Fig.5 Effect of current on q-axis inductance under different vector angle
当负载电流大小一定时,交直轴电感都会随着矢量角γ的增加而降低,如图6所示。由于交轴电流iq对直轴磁路的饱和程度影响不大,在分析直轴电感Ld的变化时仅需关注直轴电流id的变化。如图6(a),当0°<γ<90°时,随着γ增大去磁效果减弱,Ld越小;当90°<γ<180°时,id的性质由去磁变为增磁,磁路更加饱和,Ld进一步减小。当γ=90°时,id=0,不同负载电流下Ld几乎相等。
与直轴磁路相比,交轴磁路受交叉饱和的影响较大,对Lq的变化趋势进行分析时不仅需要关注交轴自身的电流iq,还必须考虑直轴电流id的影响。如图6(b),可以看出不同负载电流对应的Lq在γ=60°左右时发生重合,具体原因分析如下:当0°<γ<60°时,尽管iq使交轴磁路的饱和程度增加,但id的去磁作用占主导,因此在γ一定时,is越大Lq也就越大;当60°<γ<90°时,随着γ的增加,iq增大,iq的增磁作用超过了id的去磁作用,因此Lq会随着is的增大而减小;当90°<γ<180°时,除了iq会增加交轴磁路的饱和程度以外,id由去磁转变为增磁,Lq继续下降。
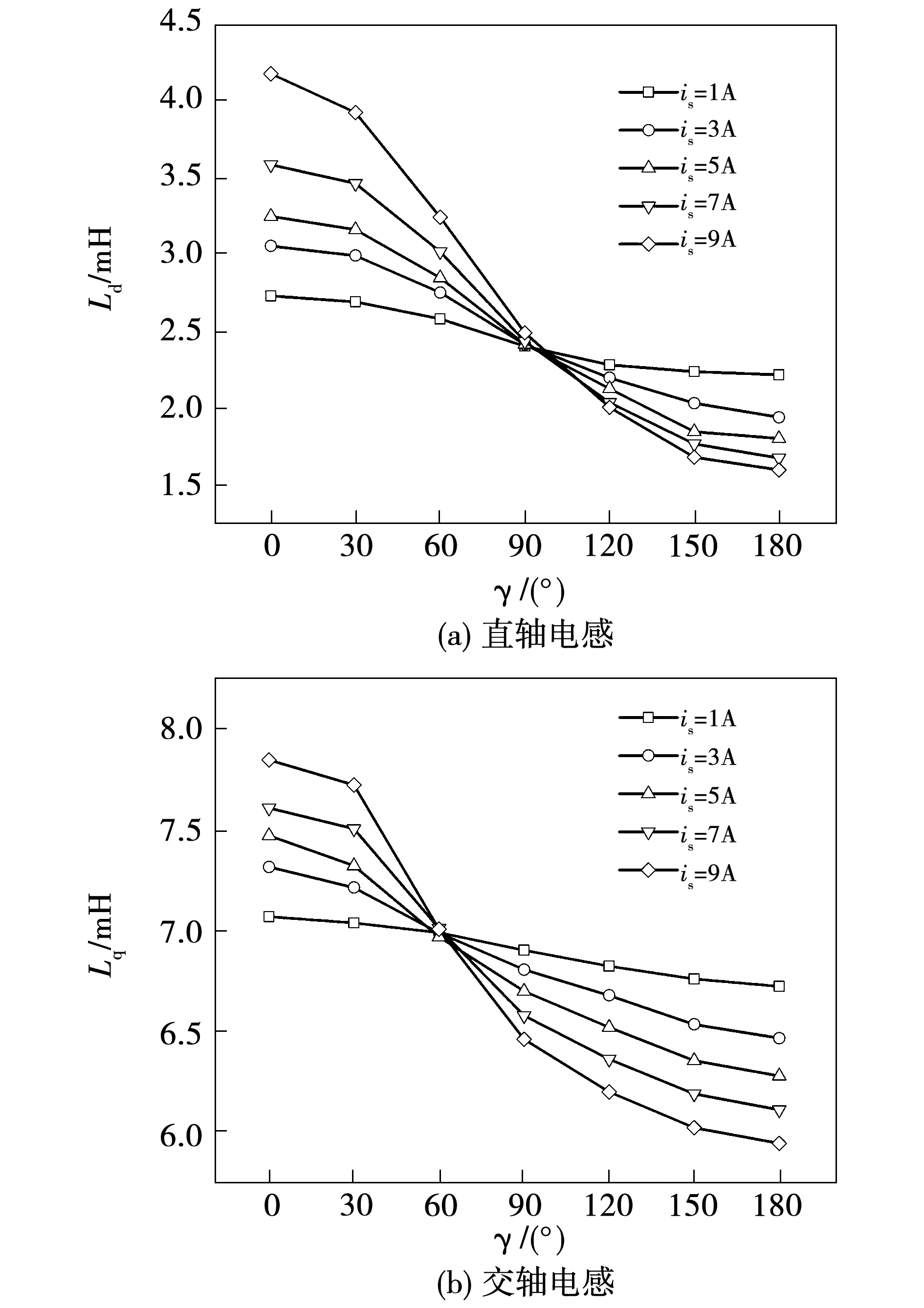
图6 不同电流下矢量角对交直轴电感的影响Fig.6 Effect of vector angle on dq-axis inductance under different current
以上计算的均为交直轴的增量电感。由于永磁体的存在,电机直轴磁路接近饱和区,同时受交叉饱和的影响,交轴磁路的工作点也可能进入到饱和区,此时增量电感更能够反映电机的动态性能。
2.4 增量电感和视在电感对比分析
为了更加清晰地剖析永磁同步电机视在电感和增量电感的关系,将电机的永磁体用空气来替代,以消除永磁体磁链的影响,仅考虑绕组电流产生的磁链对交直轴磁路的作用,从而全面对两种电感进行对比和分析。
当交轴电流iq=0,直轴电流id在[0,10A]范围内变化时,计算出交直轴的视在电感和增量电感变化曲线如图7所示。
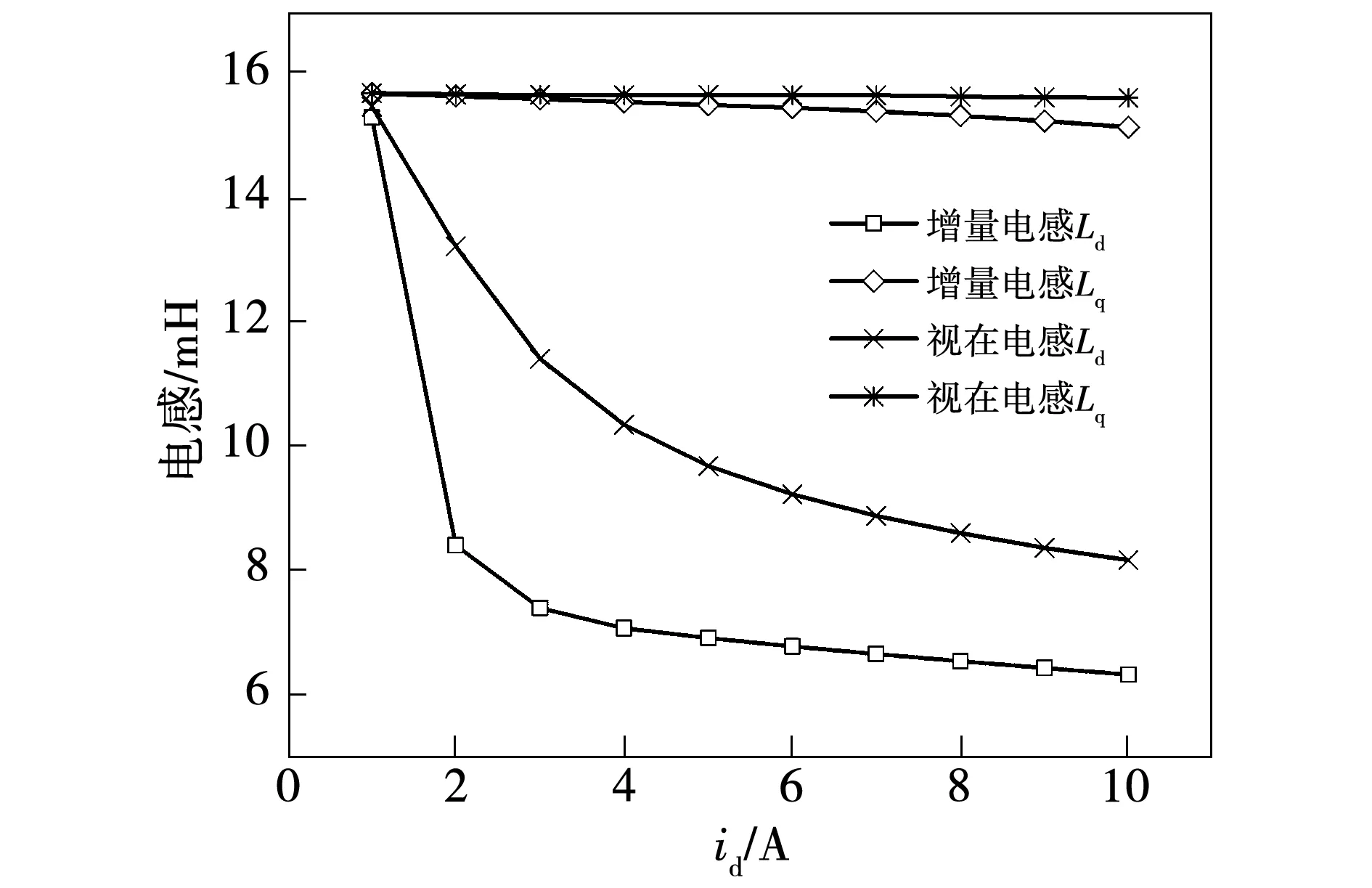
图7 视在电感和增量电感计算结果对比图(iq=0)Fig.7 Comparison curve of apparent inductance and incremental inductance(iq=0)
从图7可以看出,不管是视在电感还是增量电感,Lq都整体大于Ld,这和充磁的情况相似。同时可以看出,在1A附近时,Ld跟Lq接近,由于在电流较小时,交直轴磁路均未饱和,且离磁化特性曲线的原点很近,其斜率也近似。
交轴的视在电感和增量电感随直轴电流id变化不大,这与正常充磁情况下的规律不同。直轴的视在电感和增量电感均在下降,且增量电感降得更快。由于直轴的磁通会随着id增加而变大,磁路逐渐饱和,因此Ld会下降;根据视在电感和增量电感的定义,随着磁路饱和程度的上升,磁化曲线的斜率会逐渐变小,因此增量电感要小于视在电感,当材料深度饱和时,磁导率约等于空气磁导率,如图7所示,直轴增量电感的减小也符合先快后慢的趋势。
当直轴电流id=0,交轴电流iq在[0,10A]范围内变化时,计算出交直轴的视在电感和增量电感变化曲线,如图8所示。可以看出,两种电感Lq均略大于Ld,其中视在电感在区间内先小幅上升,然后再下降,整体变化不大,而增量电感能够反映视在电感的变化趋势,因此增量电感下降得更加明显。
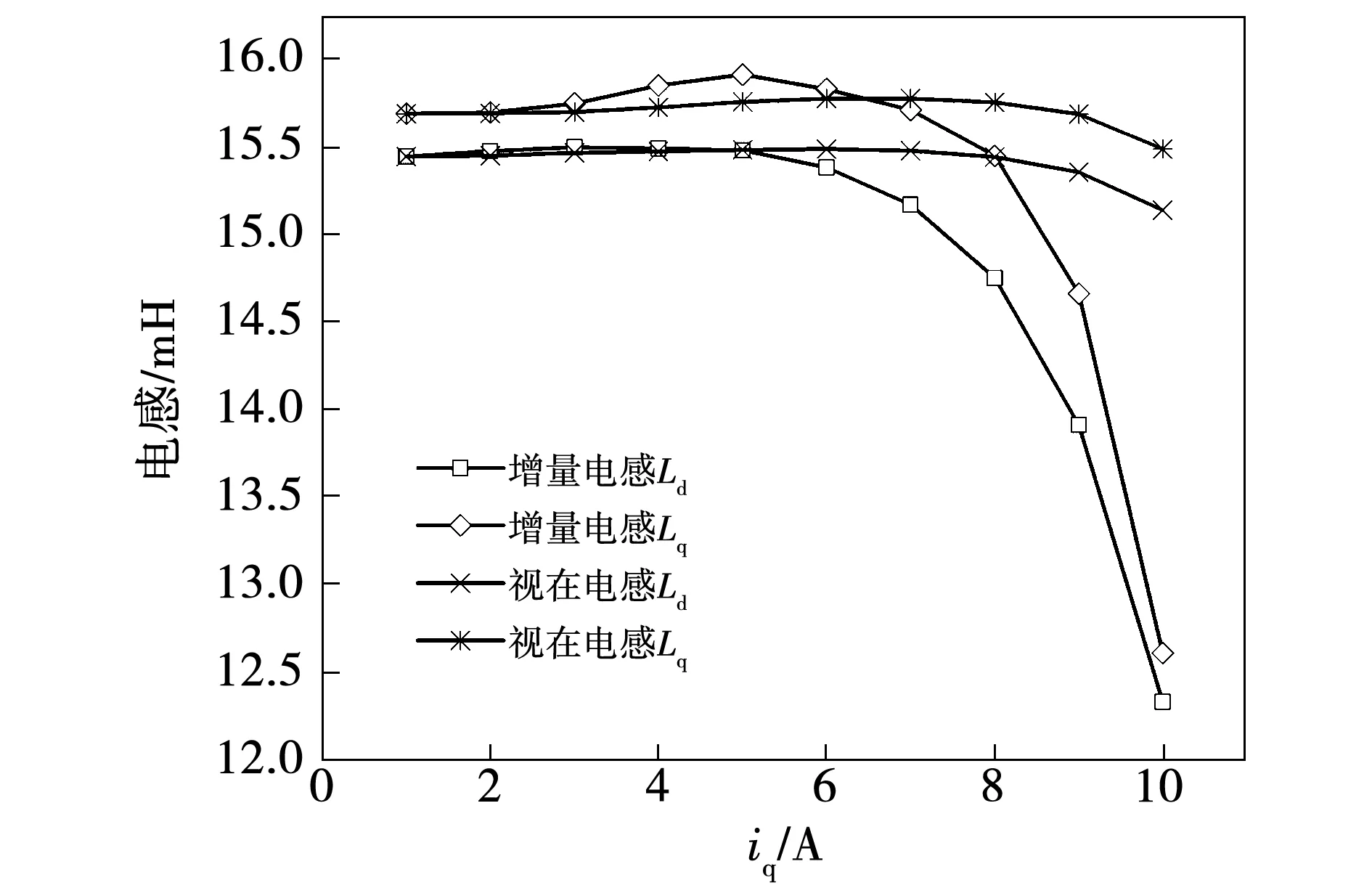
图8 视在电感和增量电感结果对比图(id=0)Fig.8 Comparison curve of apparent inductance and incremental inductance(id=0)
对比图7和图8可以看出,相较于Ld随id的上升迅速下降,iq对Lq的影响并不明显,可知交轴磁路随着iq的上升饱和程度变化不大,由于交轴磁路磁阻小,在相同磁动势激励下,能容纳更多的磁通,不易进入饱和区。Ld随iq也是相同变化规律,可见iq对直轴磁路影响不大,结合图8中随着id上升Lq几乎不变,表明在没有永磁体时,交直轴之间的交叉饱和影响并不明显,可以忽略不计。
3 交直轴电感实验测量及对比分析
为了验证上述理论分析和仿真计算的正确性,本文采用了几种常用交直轴电感的离线测量和辨识方法进行了实验验证。电感的离线测量方法大致可以分为两类,一类是基于LCR表等常用阻抗测量仪器进行线端电感测量,再经过理论上的变换得到交直轴电感,本文称这一类方法为离线测量法;另一类是在电机绕组中注入特定的激励,将激励与响应的数值带入电机的数学模型中求得交直轴电感值,本文称这一类方法为离线辨识法。下面分别对两类方法进行介绍。
3.1 离线测量法
离线测量法为实验室最基本和最容易操作的一种方法。LCR表是以微处理器控制的数字式测量仪器,用来测量各种无源阻抗参数。目前,大多LCR表的测试回路采用自动平衡电桥法[17],其基本测量原理如图9所示。
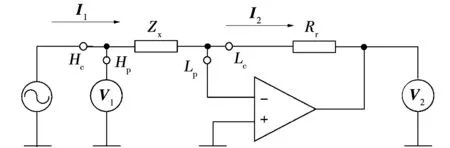
图9 基本测量原理框图Fig.9 Basic measurement principle block diagram
测试信号由Hc端加到被测阻抗Zx上,Hp端测得高端电压V1,流过Zx的电流为I1,电流流过Zx后,送到输入单元。在输入单元中,电流流过标准电阻Rr,当电桥平衡时,流过Zx的电流全部流过标准电阻Rr,即电流I1=I2,经过放大电路把I2转换为电压V2。所以根据测量得到的高端电压V1,Rr上的电压V2,即可计算出被测件的阻抗
(7)
阻抗的实部对应电阻,虚部对应电抗。由公式X=2πfL可得到在测量频率f下的电感值
(8)
以上为LCR表测量电感的原理,在实际应用时,用LCR表测量电机的三相绕组电感,根据相关理论可转换为电机的交直轴电感。
已知三相静止坐标系上的永磁同步电机电感矩阵为
(9)
根据文献[18],永磁同步电机的三相定子自感的表达式分别为:
(10)
式中:Ls0为气隙磁通所引起的自感分量;Ls2为转子凸极特性导致气隙不均匀所引起的二次谐波自感分量幅值。
永磁同步电机的三相定子互感的表达式为:
(11)
将永磁同步电机的三相定子自感以及互感的表达式代入电感矩阵方程后,对其进行坐标变换,可以得到交直轴电感的表达式分别为:
(12)
文献[18]提出了采用等效阻抗法测量永磁同步电机交直轴电感。通过手动转动转子,结合LCR表找到电机定子任意两相或三相间阻抗模为最大和最小的最小值的位置,并在这些位置测量出它们的等效电感,根据推导出的公式计算出电机的交直轴电感。等效阻抗法测量结果如表2所示。
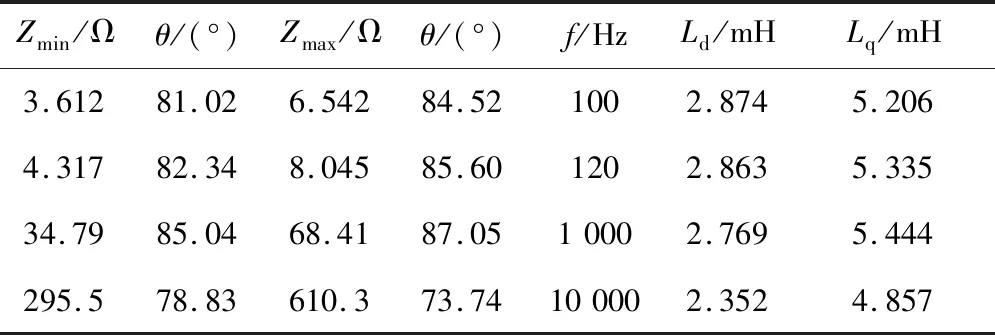
表2 等效阻抗法测量结果Table 2 Measurements of equivalent impedance method
文献[19]提出线电感法测量永磁同步电机交直轴电感。采用线电感法时,测量转子在任意位置下ABC三相绕组的线电感,根据推导出的公式同样可计算得到电机的交直轴电感,测量结果如表3所示。
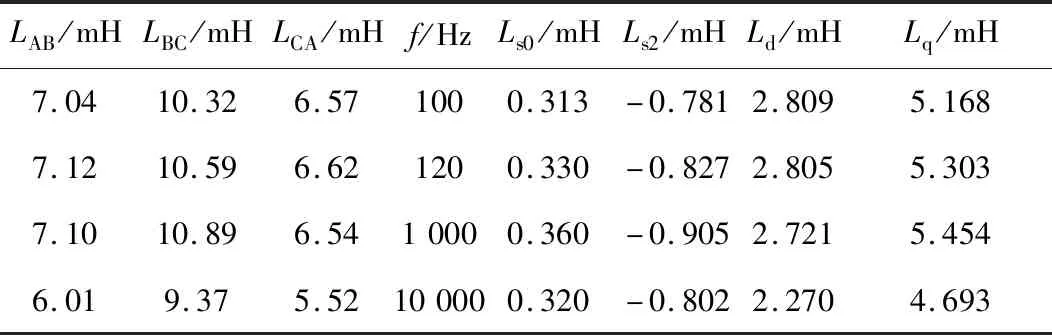
表3 充磁电机线电感法测量结果Table 3 Measurements of line inductance method magnetized motor
从表2和表3中可以看出,两种利用LCR表离线测量电感的方法具有很好的一致性。另外对于同一种方法,电感的大小与测试频率有关,由于铁心磁导率随着频率增加而降低,测试频率越大电感越小。通过与上文有限元计算的结果对比可以发现,离线测量法的结果与计算的增量电感大小较为接近。当永磁体充磁后,电机磁路的磁链存在基值,结合LCR表的测量原理,可知离线测量法测量的是永磁同步电机的增量电感。
为了进一步验证理论分析和仿真计算结果,另取一台经过消磁处理的电机来类比有限元计算中永磁体未充磁的电机模型,其他参数均保持一致,使用线电感法得到的测量结果如表4所示。
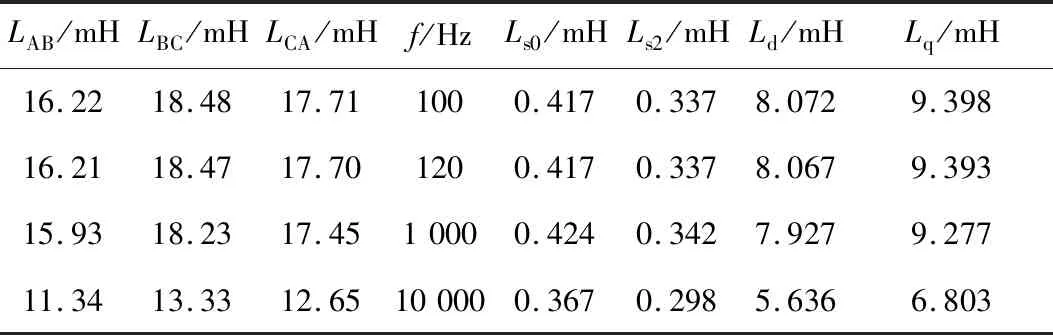
表4 去磁电机线电感法测量结果Table 4 Measurements of line inductance method of demagnetized motor
可以看出,相较于充磁的电机而言,因为退磁后永磁体的磁导率变大,磁路磁阻减小,所以去磁电机的直轴电感和交轴电感均明显变大,但和有限元计算的结果对比测量值又偏小,说明该电机并未做到完全去磁,表现出弱凸极效应,符合实际情况。
3.2 离线辨识法
文献[20]提出了一种在电机静止状态下辨识出电机的电感参数的方法。考虑到磁链的饱和程度对电感辨识结果的影响,先在电机中注入一直流电流,激励起电机磁链,然后在此直流信号上叠加一幅值较小的交流信号,通过电流、电压中的交流成分即可计算出电机在此饱和程度下的互感。本文采用此方法对所研究的永磁同步电机进行了电感离线辨识,定子电流的实验波形如图10所示。
为了在辨识过程中使永磁同步电机不产生旋转转矩,该方法在电机的直轴中注入直流电流Id。采用以上方法辨识得到的充磁电机和去磁电机的交直轴电感值如图11所示。
从以上结果可以看出,不管充磁电机还是去磁电机,直轴电感Ld和交轴电感Lq都随着直轴电流Id的增大而减小,且去磁电机的Ld和Lq均大于充磁电机,相较于充磁电机二者更为接近,其中Lq仅略大于Ld,这和有限元计算以及离线测量法得到的结论相符。
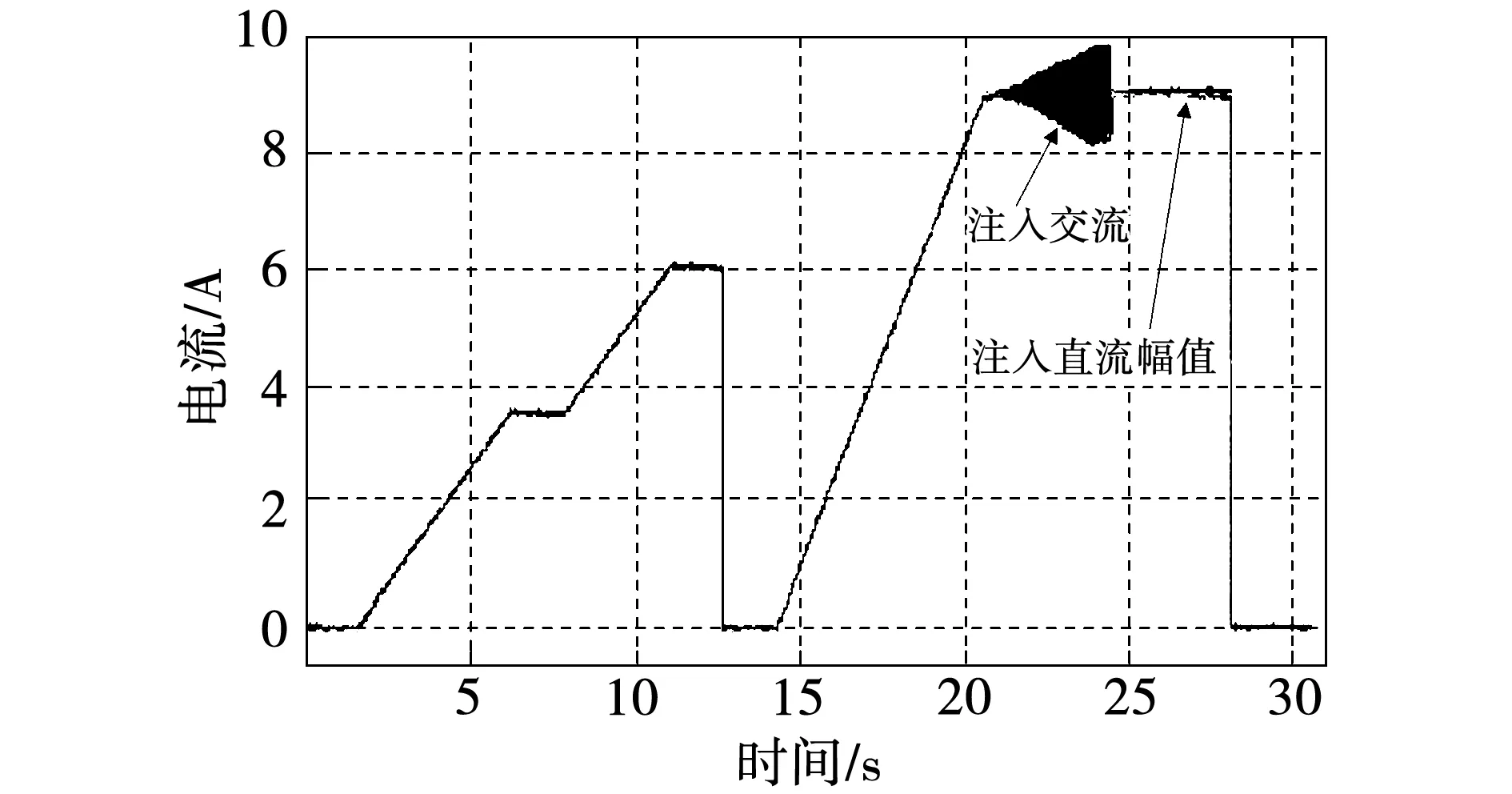
图10 定子电流的实验波形Fig.10 Experimental waveform of stator current
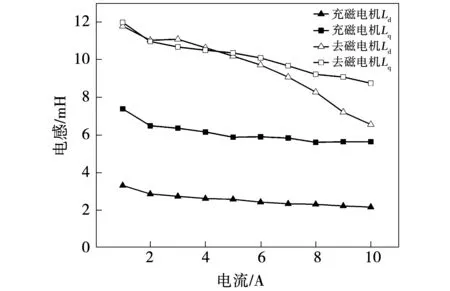
图11 交直轴电感参数辨识结果Fig.11 Estimated dq-axis inductance parameter
为了进一步验证该方法辨识出的电感类型,将以上离线辨识的结果与有限元仿真在相同电流激励条件下计算出的交直轴增量电感进行对比,如图12所示。
从图10中可以看出,相较于交轴电感Lq,直轴电感Ld的离线辨识结果与有限元计算值存在较大误差,由于有限元计算是基于完全理想的电机模型,而实测电机的永磁体存在一定程度的退磁,导致辨识出的直轴电感比理论值偏大。通过两种方法的相互验证,说明离线辨识法能够较准确地测量出永磁同步电机的交直轴增量电感,也有效支撑了前面基于有限元法的电感理论分析。
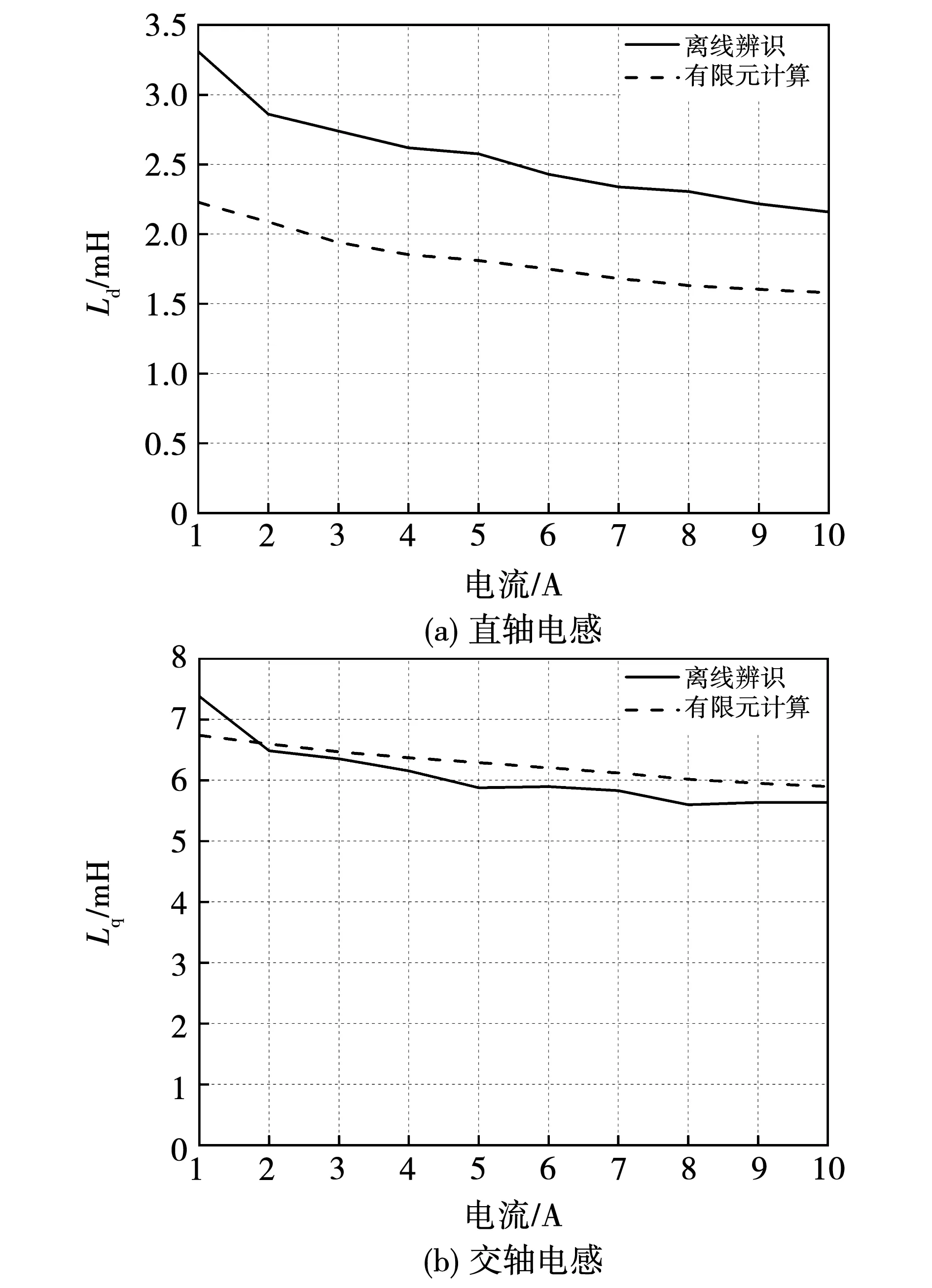
图12 离线辨识和有限元计算结果对比Fig.12 Comparison of off-line estimation and finite element method
4 结 论
1)交轴磁路和直轴磁路存在交叉饱和,但相互影响的程度不同。由于永磁体位于直轴磁路上,导致直轴电流对交轴电感的影响较大,而交轴电流对直轴电感的影响较小,即交轴磁路受交叉饱和的影响更严重。
2)电机的交直轴磁路由于永磁体的存在已经饱和,对未充磁电机的进行计算能做到只考虑绕组电流的影响,从而校验增量电感和视在电感的关系。结果表明磁路饱和时视在电感和增量电感的变化趋势相同,但增量电感的变化更加明显,符合绕组铁心的磁化特性。
3)由于永磁同步电机的空载磁场由永磁体产生,基于电桥法和交直流注入法所测量和辨识的电感均为增量电感。无论是实验测量结果之间,还是实验结果与有限元计算结果之间,都具有较好的一致性,有效验证了有限元计算分析永磁同步电机绕组电感问题的可靠性。

